Основы математической логики и теории алгоритмов
Подождите немного. Документ загружается.


Приведенные свойства определяют, конечно, не строгое понятие алгоритма,
которое называется интуитивным. Оно практически не вызывает разногласий
относительно того, является ли данный процесс алгоритмическим. Однако ситуация
существенно изменяется, если есть предположение об алгоритмической
неразрешимости задачи, т.е. о невозможности решить ее алгоритмическими
методами.
В 20-х — 30-х годах двадцатого века предпринимались попытки формализовать
понятие алгоритма. В результате было предложено несколько моделей алгоритмов
(машины Поста и Тьюринга, рекурсивные функции, нормальные алгоритмы
Маркова (1954 г.) и др.). Впоследствии было установлено, что классы решаемых ими
задач совпадают, и на основании этого появился тезис о моделях алгоритмов,
опубликованный впервые Чёрчем в 1936 г. для класса рекурсивных функций и
носящий его имя в следующем современном виде.
Тезис Чёрча. Класс задач, решаемых в любой формальной алгоритмической
модели, совпадает с классом задач, которые могут быть решены интуитивно
алгоритмическими методами.
Тезис Чёрча доказать нельзя, поскольку интуитивное понятие алгоритма
строго не определяется.
Любое вычисление по алгоритму А можно представить в виде функции
NXf
A
:
, где
n
NX
, такой, что для любых числовых данных
Xxx
n
),...(
1
значение
),...(
1 nA
xxf
совпадает с результатом
),...(
1 n
xxA
работы алгоритма А на данных
n
xx ,...
1
. Таким образом, в классе всех функций
NXf :
, где
n
NX
, выделяется
подкласс вычислимых функций, т.е функций вида
A
f
Тем самым тезис Чёрча
утверждает, что совпадают классы вычислимых и рекурсивных функций.
Формальное определение понятия алгоритма создало предпосылки для
разработки теории алгоритмов. Прогресс вычислительной техники стимулировал
дальнейшее развитие этой теории.
Далее мы рассмотрим две основные модели вычислимости — машины
Тьюринга и рекурсивные функции, установим эквивалентность этих моделей и на
основе этих моделей укажем некоторые пределы вычислимости.
61

3.1. Машины Тьюринга
Определение и примеры. Машина Тьюринга Τ представляет собой систему,
работающую в дискретные моменты времени t = 0,1,2,... и состоящую из следующих
частей:
1. Конечная лента, разбитая на конечное число ячеек. При этом в каждый
момент времени t в ячейках записаны буквы из некоторого алфавита А = {
m
aaa ,...,
10
} (где а
0
= 0, а
1
= 1, m > 1), называемого внешними алфавитом машины.
Ячейка, в которой записан символ 0, называется пустой. В процессе работы
машины каждая ячейка может менять свое состояние путем замены приписанного
к ней символа а
i
на другой символ
Aa
l
. К существующим ячейкам можно
пристраивать неограниченное число дополнительных ячеек, которые изначально
считаются пустыми. Лента считается направленной, и ее ячейки будут
просматриваться слева направо. Таким образом, если в какой-то момент времени
лента имеет r ячеек, то состояние ленты полностью описывается словом
r
iii
aaa ...
21
,
где
1
i
a
— состояние первой (слева) ячейки,
2
i
a
— состояние второй ячейки и т.д.
2. Управляющая головка, представляющая собой устройство, которое
может перемещаться вдоль ленты так, что в каждый рассматриваемый момент
времени оно находится напротив определенной ячейки и имеет некоторое состояние
q
j
из конечного множества внутренних состоянии Q = {q
0
, q
1
,... ,q
n
} или
внутренний алфавит,
0AQ
. Состояние q
0
называется заключительным и
означает завершение работы машины, а состояние q
1
— начальным и означает
начало работы машины.
3. Программа П, т.е. совокупность выражений T(i,j) (где i = 0,...,т, j =
1,...,n), каждое из которых имеет один из следующих видов:
kji
Lqqa
(сдвиг головки, находящейся в состоянии q
j
напротив ячейки
с буквой a
i
, на одну ячейку влево с заменой состояния q
j
на q
k
);
kji
Rqqa
(сдвиг головки, находящейся в состоянии q
j
напротив ячейки
с буквой a
i
,, на одну ячейку вправо с заменой состояния q
j
на q
k
);
klji
qaqa
(замена буквы a
i
в текущей ячейке на букву a
l
, также замена
состояния q
j
головки на состояние q
k
).
Выражения T(i,j) называются командами. При этом команды не могут
62
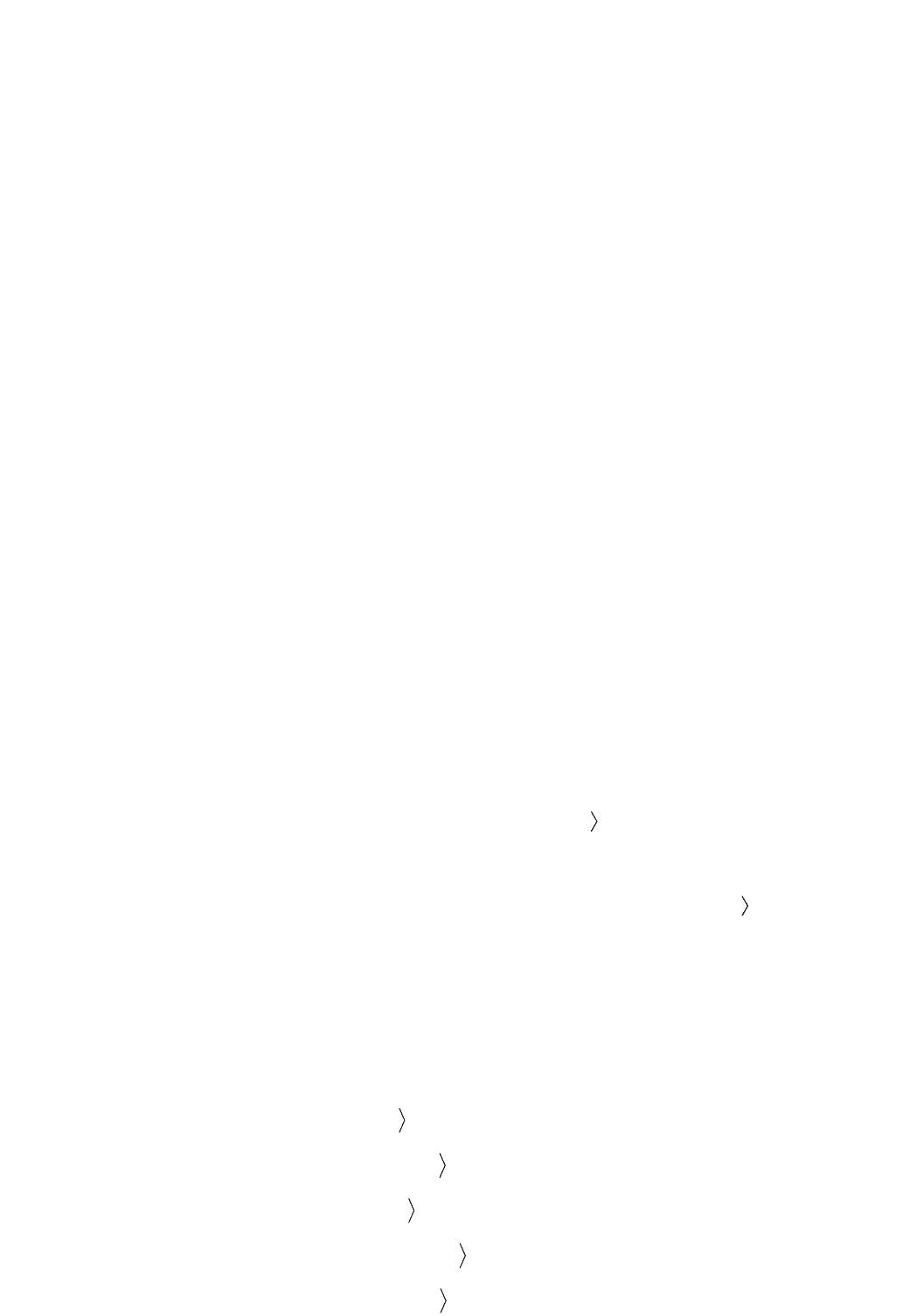
начинаться со слов a
i
q
0.
Символы L и R не принадлежат множеству AUQ.
Таким образом, машина Тьюринга Τ есть пятерка <A, Q, П, q
0
, q
1
>, а работа
машины Τ состоит в изменении ее конфигурации К, состоящей из состояния ленты,
состояния головки и положения текущей ячейки. Дискретным моментам времени t
= 0,1,2,... соответствуют конфигурации К
0
,К
1
,К
2
,--- Конфигурация К
0
называется
начальной, а конфигурация K
t
, содержащая q
0
, ~ заключительной. Конфигурации
будут задаваться в виде машинных слов Μ =
ij
aq
, где
i
a
— состояние ленты, q
j
— состояние головки, находящейся напротив ячейки с состоянием a
i
, занимающей то
же положение среди других ячеек, что и буква a
i
в слове
ij
aq
.
Опишем преобразование Μ
T
М' машинного слова Μ в машинное слово М' за
один шаг работы машины Т.
Пусть команда T(i,j) равна
kji
Lqqa
. Если
— пустое слово
, то М
2
=
ik
aaq
0
. Если же
lk
aq
, то М
2
=
ilk
aaq
.
Если T(i,j) —
kji
Rqqa
- аналогично.
Если T(i,j) = a
i
q
j
—> a
l
q
к
, полагаем М
2
=
ilk
aaq
.
Будем говорить, что машинное слово М' получается из машинного слова Μ с
помощью машины Т, и писать Μ =>
Т
Μ', если существует последовательность
преобразований M
i
—>
Т
M
i+1
, i = 0,..., к — 1, для которой М
0
= М, М
к
= М'.
Преобразование Μ =>
Т
Μ', при котором на каждом переходе M
i
—>
T
M
i+1
не
достраиваются ячейки слева, обозначается через Μ
T
Μ'.
Преобразование Μ =>
Т
Μ', при котором на каждом переходе M
i
—>
T
M
i+1
не
достраиваются ячейки ни слева, ни справа, обозначается через Μ |
T
М'. (индекс Т
можем опустить).
Зафиксируем алфавит А = {а
0
, а
1
а
2
, · , а
m
}· Через
x
i
a
будем обозначать слово
a
i
a
i
a
i
...a
i
алфавита A, состоящее из x букв a
i
. Приведем список машин, которые
будут использоваться в
дальнейшем в качестве составляющих для других машин.
1.
А (перенос нуля):
0001|0001
01
xx
qq
2. Б
+
(сдвиг вправо):
01|01
01
qaaq
x
i
x
i
3. Б
-
(сдвиг влево):
i
x
i
x
aqaq 01|01
01
4. В (транспозиция):
00101|00101
01
xyyx
qq
5. К (копирование):
00101|00001
01
xxxx
qq
63
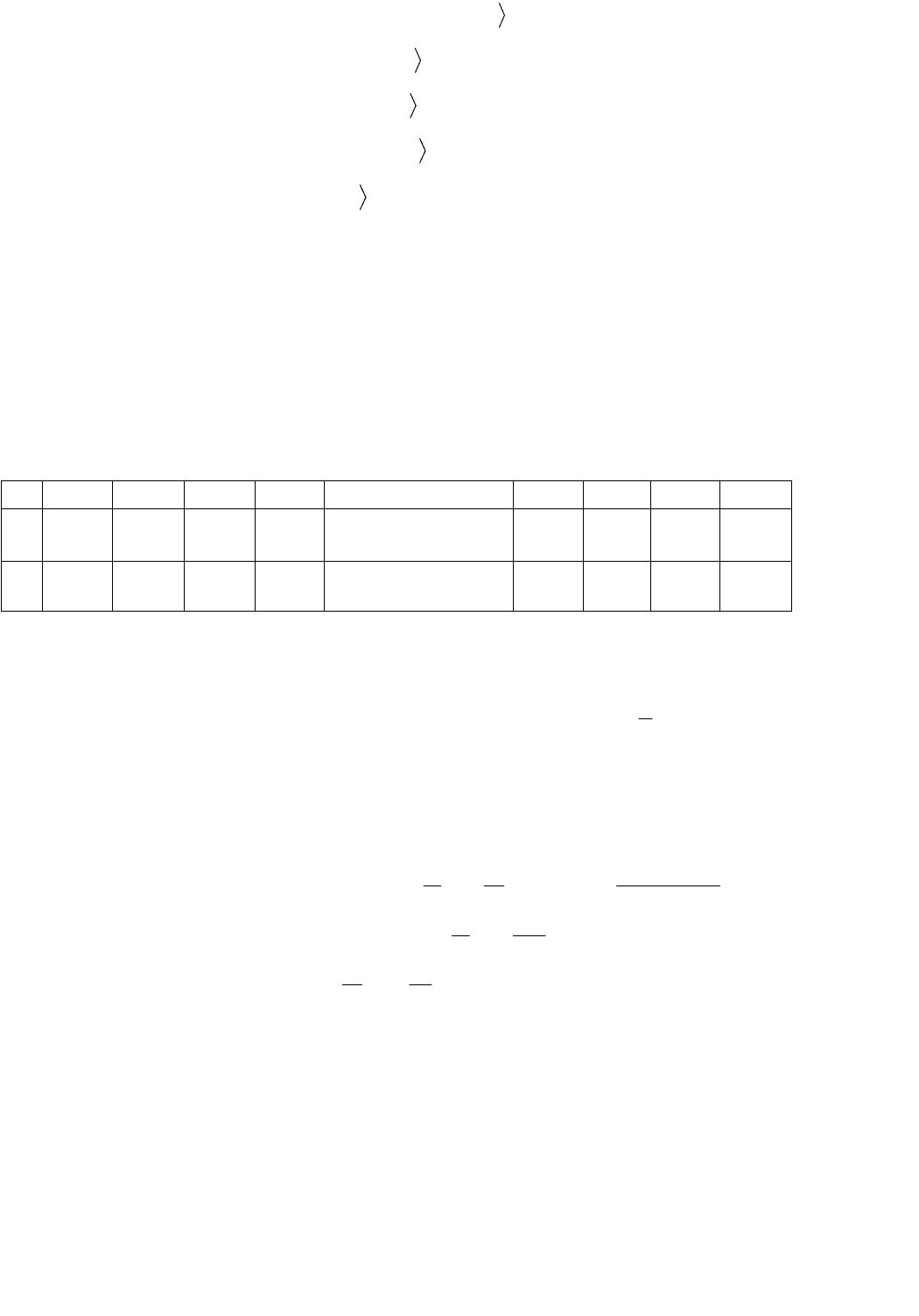
6. Л (стирающая машина):
000|001
01
xx
qq
7. R (удаление 1):
0001|001
0
1
1
xx
qq
.
8. S (добавление 1):
1
01
01|001
xx
qq
.
9. Сложение:
00001|00101
1
0
11
1
yxyx
qq
.
10. Умножение:
001|00101
1*
0
11
1
yxyx
qq
.
Приведем примеры программ для машины Сложение
Программу, соответствующую указанной схеме, представим виде следующей
таблицы команд, в которой на пересечении строки с символом
Aa
i
и столбца с
символом
0, jQq
j
, имеется запись команды перехода(для машин Тьюринга
данные или транспанированные таблицы часто описывают программы):
q
1
q
2
q
3
q
4
q
5
q
6
q
7
q
8
q
9
0 R q
2
R q
3
Lq
4
Lq
5
Lq
6
(где y=0) 0q
0
Lq
8
1q
9
0q
0
1 Rq
2
R q
3
0q
4
0q
7
(где y
0) Lq
6
Lq
8
Lq
9
3.2. Функции, вычислимые на машинах Тьюринга.
Для любого натурального числа
Nn
обозначим через
n
слово, состоящее из n +
1 числа единиц: 11... 1.
Функция
NXf :
, где
k
NX
,, называется вычислимой на машине Тьюринга T
f
=
<A, Q, П, q
0
, q
1
>, если выполняются следующие условия:
a) из
Xnn
k
,...,
1
следует
0),...,(000...00
1011 k
T
k
nnfqnnq
f
;
b) из
XNnn
k
k
\,...,
1
следует
f
T
k
nnq 00...00
11
т.е. начиная со слова
00...00
11 k
nnq
машина T
f
работает неограниченно долго,
не приходя в заключительное состояние q
0
.
Таким образом, вычислимость функции f на машине Тьюринга T
f
означает,
что по любому набору
k
nn ,...,
1
из области определения (закодированному в виде
наборов единиц длин n + 1, разделенных нулями) машина T
f
выдает значение
),...,(
1 k
nnf
(закодированное в виде набора единиц длины
1),...,(
1
k
nnf
), а для
любого набора
XNnn
k
k
\,...,
1
машина T
f
не завершает работу за конечное время.
Функция f называется правильно вычислимой на машине Тьюринга T
f
= <A,
64

Q, П, q
0
, q
1
>, если выполняются следующие условия:
a) из
Xnn
k
,...,
1
следует
0...0),...,(000...00
1011 k
T
k
nnfqnnq
f
;
b) из
XNnn
k
k
\,...,
1
следует
f
T
k
nnq 00...00
11
т.е. начиная со слова
00...00
11 k
nnq
машина T
f
работает неограниченно долго,
не приходя в заключительное состояние q
0
. и при этом не достраиваются ячейки
слева.
Функция f называется правильно вычислимой (сокращенно ПВФ), если f
правильно вычислима на некоторой машине Тьюринга.
Преимущество правильной вычислимости по сравнению с обычной
вычислимостью на машинах Тьюринга состоит в том· что левее ячейки, напротив
которой стоит головка в начальном состоянии, можно записывать информацию,
которая не изменяется в процессе "правильного вычисления".
П р и м е р 1. Нуль-функция 0-Функция о : N —> N, для которой о(х) =0,
Nx
,
правильно вычислима на машине ЛS.
2. Функция следования s : Ν —> Ν, для которой s(x) = х + 1,
Nx
,
правильно вычислима на машине S.
3. n-Местная функция проекции на т-ую координату
NNI
nn
m
:
, для
которой
nmNxxxxxI
nmn
n
m
1,,...,,),...,(
11
правильно вычислима на композиции
машин Тьюринга.
4. Функции + : Ν
2
—> Ν, +(х, у) = х +y, и · : Ν
2
—> Ν,
yxyx ),(
,
правильно вычислимы на машинах Сложение и Умножение соответственно.
Теорема 1. Если функции
),...,(
11 n
xxf
,...
),...,(
1 nm
xxf
и
),...,(
1 m
yyg
правильно
вычислимы, то функция
)),...,(),...,...,((),...,(
1111 nmnn
xxfxxfgxxh
правильно вычислима.
3.3.Рекурсивные функции и отношения
3.3.1. Примитивно рекурсивные функции.
Рассмотрим сначала всюду определенные числовые функции
65

}0{\,: NkNNf
k
, т.е не нуль-местные операции на множестве Ν, и определим
понятие примитивно рекурсивной функции (сокращенно ПРФ).
Функции о(х), s(x),
nmxxI
n
n
m
1),,...,(
1
, называются простейшими
примитивно рекурсивными функциями.
Пусть f— m-местная операция, g
1
,...,g
m
- n-местные операции на множестве
N. Оператор S, ставящий в соответствие операциям f и g
1
,...,g
m
n-местную
операцию h, удовлетворяющую тождеству
)),...,(),...,...,((),...,(
1111 nmnn
xxgxxgfxxh
называется оператором суперпозиции (подстановки). При этом всюду
определенная функция
h = S(f, g
1
,...,g
m
)
является, очевидно, суперпозицией функций f и g
1
,...,g
m
.
Оператор примитивной рекурсии R каждой (п + 2)-местной операции f и n-
местной операции g на множестве N ставит в соответствие (п + 1)-местную
операцию
h=R(f,g)
удовлетворяющую следующей схеме примитивной рекурсии:
Для n = 0 схема примитивной рекурсии имеет следующий вид:
))(,()1(
)0(
yhyfyh
ah
,
где a — постоянная одноместная функция, равная числу а.
Схема примитивной рекурсии образует некоторый индукционный процесс
построения функции h, при котором на нулевом шаге используется функция g, а на
каждом последующем шаге значение функции f от аргументов x
1
,... ,х
m
,, номера у
предыдущего шага и значения функции h, вычисленного на предыдущем шаге.
),,...,
1
(,,,...,
1
()1,,...,
1
(
),...,
1
()0,,...,
1
(
y
n
xxhy
n
xxfy
n
xxh
n
xxg
n
xxh
66
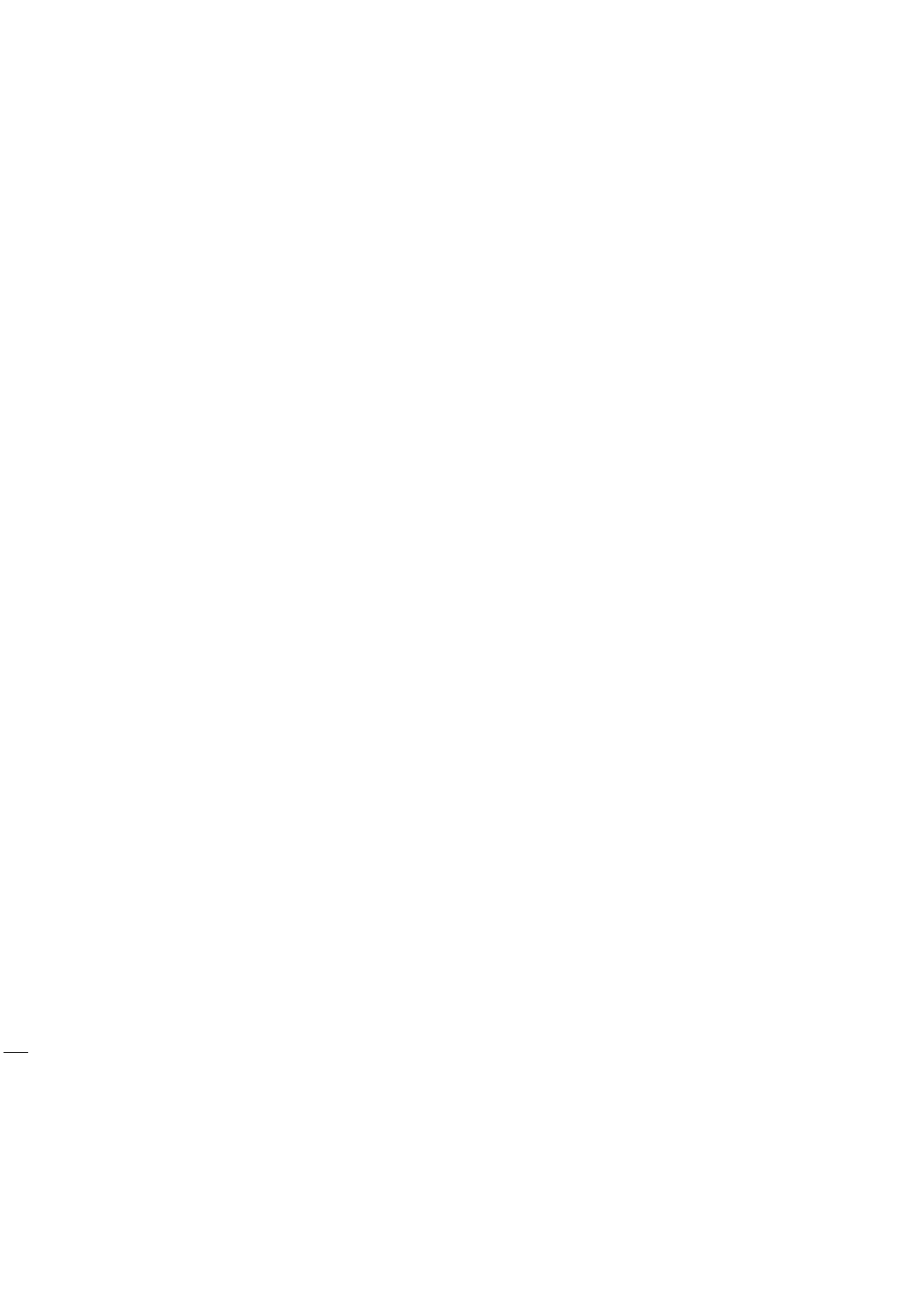
Функция f называется примитивно рекурсивной, если существует
последовательность функций f
0
, · · ·, f
n
,в которой f
n
= f и всякая функция f
i
является
простейшей ПРФ или получается из предыдущих функций с помощью оператора
суперпозиции S или оператора примитивной рекурсии R.
П р и м е р 1. Функция сложения χ + у примитивно рекурсивна в силу схемы
примитивной рекурсии
)()1(
)(0
1
1
yxsyx
xIx
2. Схема примитивной рекурсии
xyxyx
xox
)1(
)(0
обосновывает примитивную рекурсивность функции умножения
yx
.
Доказательство примитивной рекурсивности следующих функций оставляется
в качестве упражнения.
3. х
у
, где 0
0
= 1, — функция возведения в степень.
4. х!, где 0! = 1, — Х-факториал.
5.
знак числа х
6.
дополнение знака числа х
7. \х — у\ — модуль разности.
8. max(x, у) — максимум чисел x и у. \
9 min(x,y) — минимум чисел x и у.
10 [х/у], где [х/0] = x — частное от деления x на у.
0,1
,0,0
)(
xесли
xесли
xsg
0,0
,0,1
)(
xесли
xесли
xsg
67
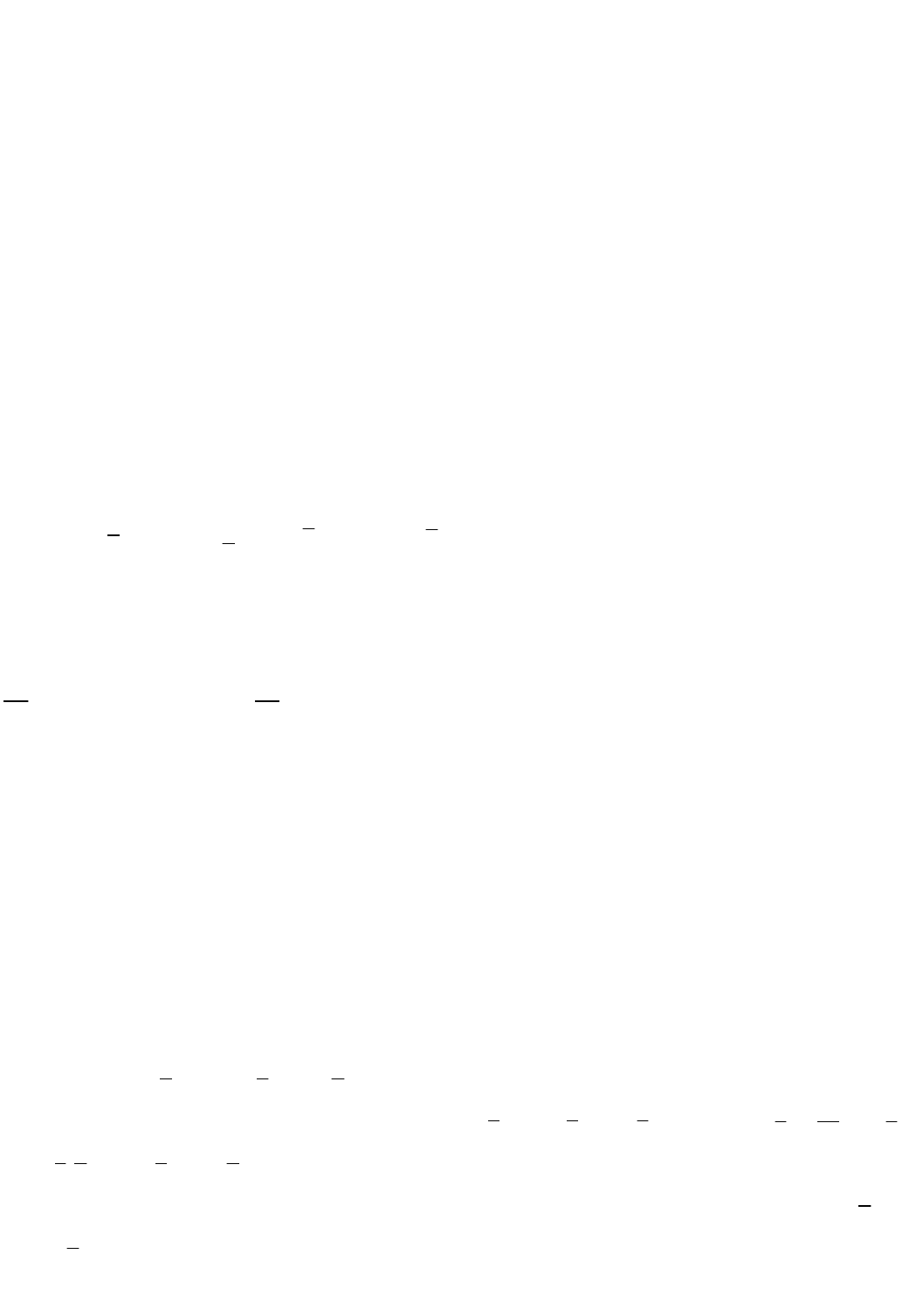
11. rest(:r, у), где rest(x, 0) = x, — остаток от деления x на у.
Пусть f(x
1
,... ,x
n
,i) — (n + 1)-местная операция на множестве N. Определим
операторы суммирования и произведения:
y
i
nn
ixxfyxxg
0
111
),,...,(),,...,(
y
i
nn
ixxfyxxg
0
112
),,...,(),,...,(
Предложение 1. Если f — примитивно рекурсивная функция, то функции g
1
,g
2
,
примитивно рекурсивны
3.3.2. Примитивно рекурсивные отношения.
Отношение
k
NP
называется примитивно рекурсивным (сокращенно ПРО),
если примитивно рекурсивна характеристическая функция
Px
Pxесли
x
P
,0
,1
)(
, где
),...,(
1 k
xxx
П р и м е р 1. Отношения равенства x = у и делимости х|у (х делит у)
примитивно рекурсивны. Действительно, характеристические функции χ
=
(x,у) =
sg
(|х — у|) и X
|
(x,y)=
sg
(rest(y, x)) примитивно рекурсивны.
Покажем, что теоретико-множественные операции над ПРО сохраняют
примитивную рекурсивность.
Пусть Р, Q
k
N
— некоторые отношения. Положим
QPQP
,
QPQP
,
PNP
k
\
,
QPQP
Предложение 2. Если P,Q
k
N
и
l
NR
- примитивно рекурсивные
отношения, то отношения
QP
,
QP
,
P
,
QP
,
RP
примитивно
рекурсивны.
Д о к а з а т е л ь с т в о . Поскольку по условию примитивно рекурсивны
функции
)(x
P
,
)(x
Q
,
)(y
R
примитивно рекурсивными являются также
характеристические функции
)()()( xxx
QPQP
,
))(()( xsgx
PP
)()(),( yxyx
RPRP
. Теперь из соотношений
QPQP
и
QPQP
вытекает примитивная рекурсивность характеристических функций
)(x
QP
и
)(x
QP
□
Записи (
yz
) и (
yz
) называются ограниченными кванторами. Пусть Ρ
68
1
k
N
— некоторое отношение. Обозначим через (
yz
)Ρ(x
1
,... ,x
n
,z) (k + 1)-
местное отношение {
bслюбогодляPcaabaa
kk
),,...,(|),,...,(
11
}, через (
yz
)Ρ(x
1
,... ,x
n
,z) (k + 1)-местное отношение {
bснекоторогодляPcaabaa
kk
),,...,(|),,...,(
11
}
Следующее утверждение показывает, что примитивная рекурсивность
отношений сохраняется при навешивании ограниченных кванторов.
Предложение 3. Если Ρ
1
n
N
— примитивно рекурсивное отношение, то
отношения Q
1
=(
yz
)Ρ(x
1
,... ,x
n
,z) и Q
2
= (
yz
)Ρ(x
1
,... ,x
n
,z) примитивно
рекурсивны.
Д о к а з а т е л ь с т в о . Примитивная рекурсивность отношений Q
1
и Q
2
вытекает из следующих соотношений:
y
i
PQ
ixyx
0
),(),(
1
)),((),(
0
2
y
i
PQ
ixsgyx
где
),...,(
1 k
xxx
П р и м е р 1. Поскольку справедливо соотношение
)( yzyx
(x+z = у),
отношение
yx
примитивно рекурсивно в силу предложения 3.
2. Аналогично из
))()(( yzxsyzyx
вытекает примитивная
рекурсивность отношения x< у.
Пусть
(
x
) — некоторая k-местная операция на множестве Ν, Ρ
1
k
N
.
Обозначим через
),())(( yxPxy
k-местную операцию, значение которой на
наборе x равно
случае. противном в 1 + )(
, )( некоторого у)для Р(х, если }, ),())(( |min{y
x
xyyxPxy
Оператор, ставящий в соответствие каждой операции
-к-местной
операции и отношению Ρ
1
k
N
операцию
),())((),( yxPxyP
называется
оператором ограниченной минимизации.
Предложение 4. Если
(
x
) - ПРФ, Ρ
1
k
N
- ПРО, то
),( P
- ПРФ.
П р и м е р 3. Функция
x
которая каждому натуральному числу x ставит в
соответствие целую часть от квадратного корня из х, примитивно рекурсивна в силу
предложения 4, поскольку
))()((][
2
ySxxyx
.
69

Примеры ПРФ. Нумерации кортежей натуральных чисел. Нумерацией
множества X называется любая сюръекция ν: X —>N. Представлена
"диагональная" нумерация множества Ν
2
, устанавливающая биекцию между
множествами N и Ν
2
. Отображение с : Ν
2
—> Ν, ставящее в соответствие
каждой паре натуральных чисел (х, у) ее "диагональный" номер с(х, у),
называется канторовской нумерующей функцией.
2
3)(
),(
2
yxyx
yxc
Т.е. пары (0,0), (0,1), (1,0), (0,2), (1,1), (2,0), (0,3),
По номеру n = с(х, у) однозначно определяются его левая координата 1(n) =x
и правая координата r(n) = у.
Функции с, l и r удовлетворяют следующим тождествам:
с(1(п),r(п)) = п, 1(с(х,у)) = х, r(с(х,у)) = у.
Данные функции ПРФ.
3.3.3. Частично рекурсивные функции.
Будем говорить, что функция f(
x
) получается из функций g(
x
, у) и h(
x
, у)
с помощью оператора минимизации М, и обозначать f(
x
) = μy (g(
x
, у)
h(
x
,
у)) или F(
x
)
=
M(g(
x
,y),h(
x
,y)), если выполнено следующее условие
:
f(
x
)
определено и равно у тогда и только тогда, когда определены g(
x
, 0), h(
x
, 0), ..., g(
x
, у), h(
x
, у) и справедливы соотношения g(
x
, i) > h(
x
, i), i = 0,..., у - 1, g(
x
, у)
h(
x
, у).
Функция f : X —> N
k
называется частично рекурсивной (ЧРФ), если она может
быть получена из простейших ПРФ с помощью конечного числа применений
операторов S, R и М. Частично рекурсивная функция называется рекурсивной (РФ),
если она всюду определена.
Обозначим через М°(g, h) значение М(g, h), если функции g, h и М(g, h) всюду
определены.
Функция f: X —> N
k
называется общерекурсивной (ОРФ), если она может быть
получена из простейших ПРФ с помощью конечного числа применений операторов
S, R и М°.
Класс ЧРФ строго содержит класс РФ, поскольку, например, нигде не
70
