Обработка материалов давлением. Сборник научных трудов. №19

Подождите немного. Документ загружается.

Обработка материалов давлением №1 (19), 2008 291

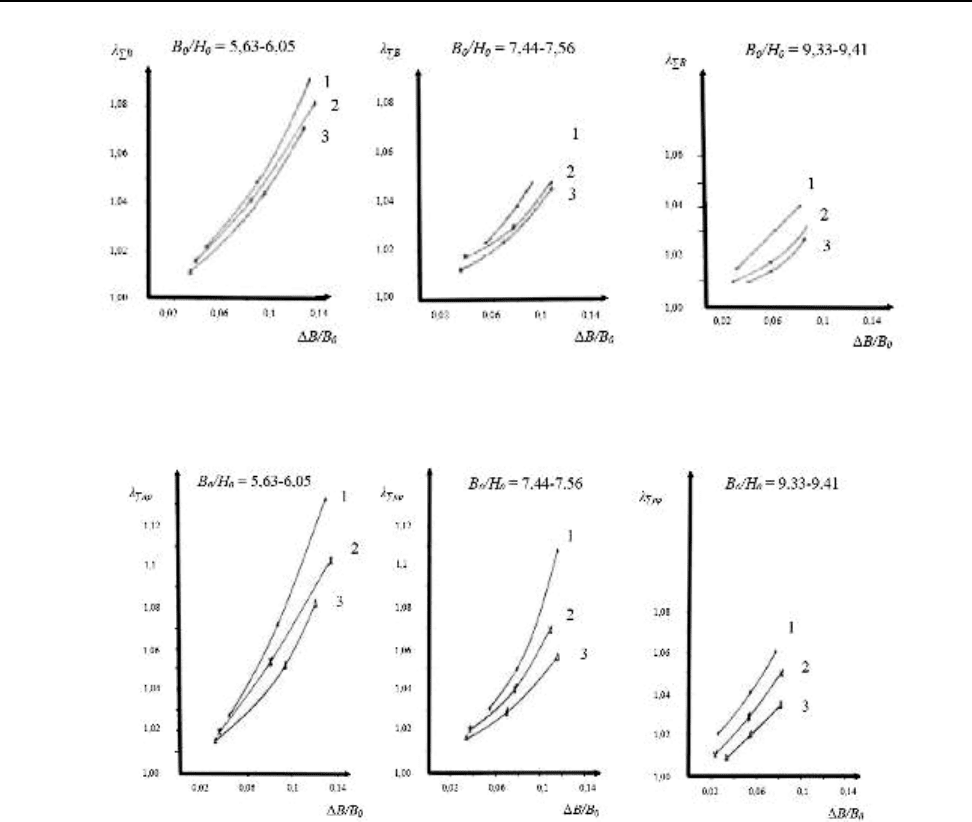
Рис. 1. Зависимость коэффициента суммарной вытяжки в вертикальных валках от

∆B/B

при прокатке в калибрах:

1 – калибр №1; 2 – калибр №2; 3 – калибр №3.

Рис. 2. Зависимость коэффициента суммарной вытяжки после проглаживания от

∆B/B

при прокатке в калибрах:

1 – калибр №1; 2 – калибр №2; 3 – калибр №3.

ЛИТЕРАТУРА

1. Чуманов Ю.М. Исследование ребрового обжатия плоского сляба в ящичном калибре /

Ю.М. Чуманов, Г.М. Шульгин, В.Ф. Губайдуллин и др.// Производство толстолистовой стали: Темат. отрасл.

сб. – М.: Металлургия, 1979. - №4. – С. 47-50.

2. Бобух И.А.Исследование течения металла при прокатке широких полос в вертикальных валках /

И.А. Бобух, В.И. Понамарев, Л.М. Белкин //Металлургия и коксохимия: Обработка металлов давлением. – Киев:

Техніка, 1983. – С. 48-54.

3. Руденко Е.А. Расчет силових параметров редуцирования слябов с многократными последовательными

обжатиямив вертикальних валках и ширины рас ката после

прокатки в горизонтальных валках / Е.А. Руденко,

А.П. Митьев, С.Н. Денисов // Вісник Донбаської державної машинобудівної академії. – 2006. - №1(3). – С. 89-93.

Корохов В. Г. – канд. техн. наук, гл. спец. ТО ЗАО «Донецксталь-МЗ»;

Черковер Р. А. – магистрант ДонНТУ;

Лонцкий А. Е. – магистрант ДонНТУ.

ДонНТУ – Донецкий национальный технический университет, г. Донецк.

omd@fizmet.donntu.donetsk.ua

Обработка материалов давлением №1 (19), 2008 292

УДК 621.778

Должанский А. М.

Ермакова О. С.

Ломов И. Н.

Ломова О. Б.

Петлёваный Е. А.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ НА КОНТАКТЕ

СТАЛЬНОЙ ЗАГОТОВКИ С РОЛИКОМ ОКАЛИНОЛОМАТЕЛЯ

В работах [1, 2] были представлены материалы, посвящённые теоретическому

определению условий деформации круглой заготовки в роликовом окалиноломателе.

Известные выражения выведены из уравнения баланса мощностей, в котором, в частности,

учитывается составляющая, связанная с потерями на внешнее трение. Расчёт этой

составляющей возможен при известных значениях коэффициента трения

на контакте

заготовки и поверхности ролика. Однако использование справочных данных по

является

грубым приближением, поскольку заготовка на роликах претерпевает упруго-пластический

изгиб с растяжением в присутствии отслаивающейся окалины.

Целью работы является экспериментальное определение значений коэффициента

трения, характерных для этих условий.

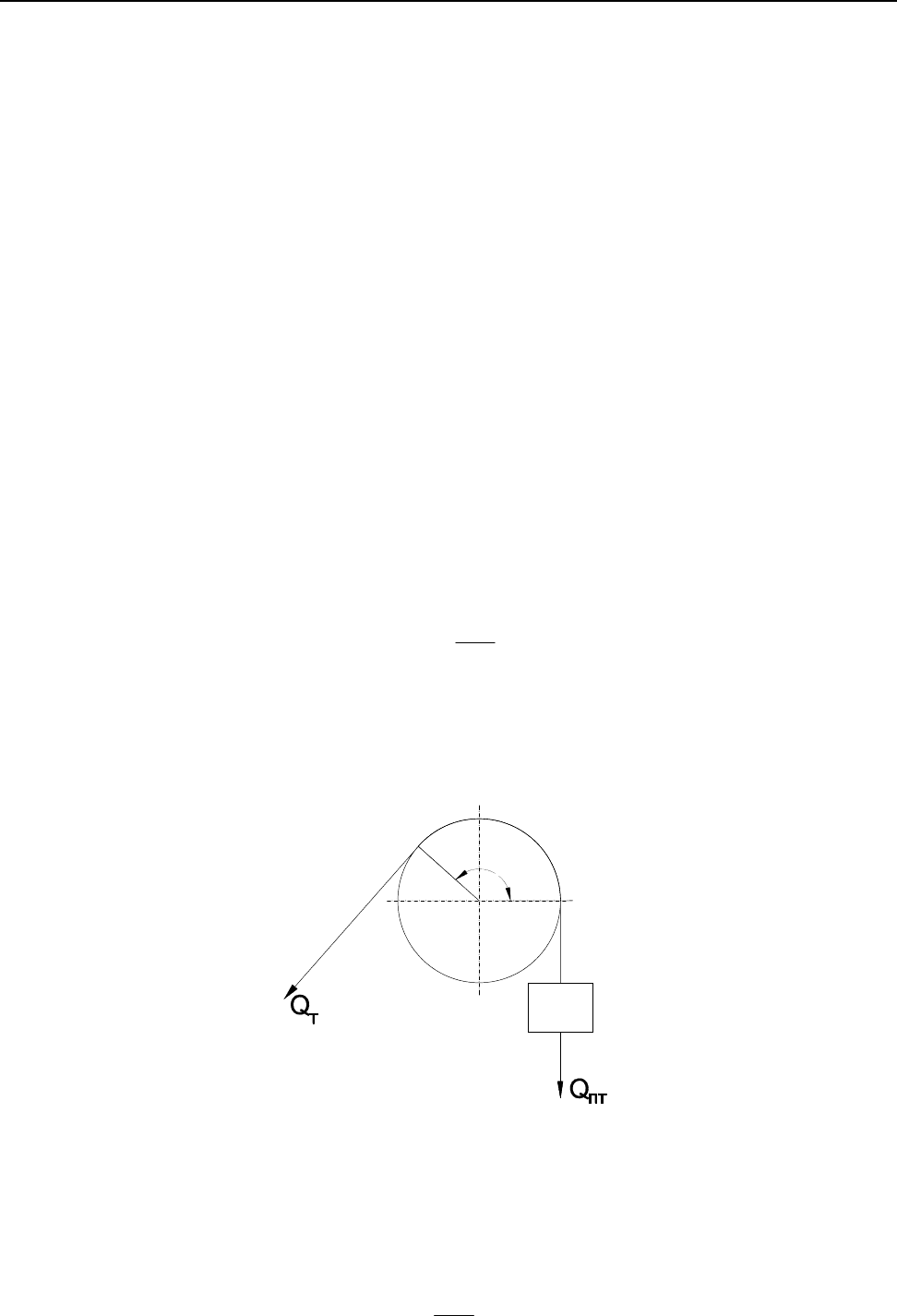
При решении поставленной задачи воспользовались моделью силового нагружения

гибкой нити на валу (рис. 1), которая описывается формулой Эйлера [3]:

пт

⋅ϕ

= , (1)

где

Q – тянущая сила;

пт

Q – сила противовеса;

φ – угол охвата вала гибкой нитью.

Рис. 1. Схема нагружения гибкой нити на валу согласно схеме Эйлера [3].

При деформировании заготовки как реального тела на ролике сила

определяется

суммой сил

пт

и упруго-пластического формоизменения металла

пу

−

[2]. Тогда

выражение (1) преобразуется к виду:

пу

пт

−

⋅ϕ

+= . (2)

Обработка материалов давлением №1 (19), 2008 293

Из равенства (2) следует:

−

−пут

пт

. (3)

Формула (3) позволяет при известных значениях величин, входящих в неё, определять

величину

При проведении соответствующих экспериментов и расчётов изготовили и

установили на цепном волочильном стане трехроликовый окалиноломатель. Его

конструкция позволяла использовать ролики диаметром D = 40…180 мм, изменять

расстояния между их осями: t – по ходу движения и y – перпендикулярно движению

обрабатываемой заготовки диаметром

заг

d, равным 6,5 мм (катанка) и 4,0 мм (передельная

заготовка).

Силу

Q определяли тензометром с записью на электронно-лучевой осциллограф

ОСЦ-15. В опытах контролировали предел текучести металла путем проведения стандартных

механических испытаний образцов металла, отобранных до и после обработки

в окалиноломателе.

Угол

ϕ охвата ролика заготовкой изменяли путем варьирования значений t и y,

с определением его величины графо-аналитическим методом в диапазоне от 40º до 180º.

Составляющие сил

пу

−

, затрачиваемой на упруго-пластический изгиб и

пт

заднего натяжения для ближайшего к тензометру ролика, вычисляли с использованием

расчётной схемы из работы [2]. При этом принято допущение, что

одинаково на всех

роликах окалиноломателя, и для первого приближения его значение равно 0,1.

Окончательное значение

получали после 4-5 итераций с обеспечением точности не

хуже 2%.

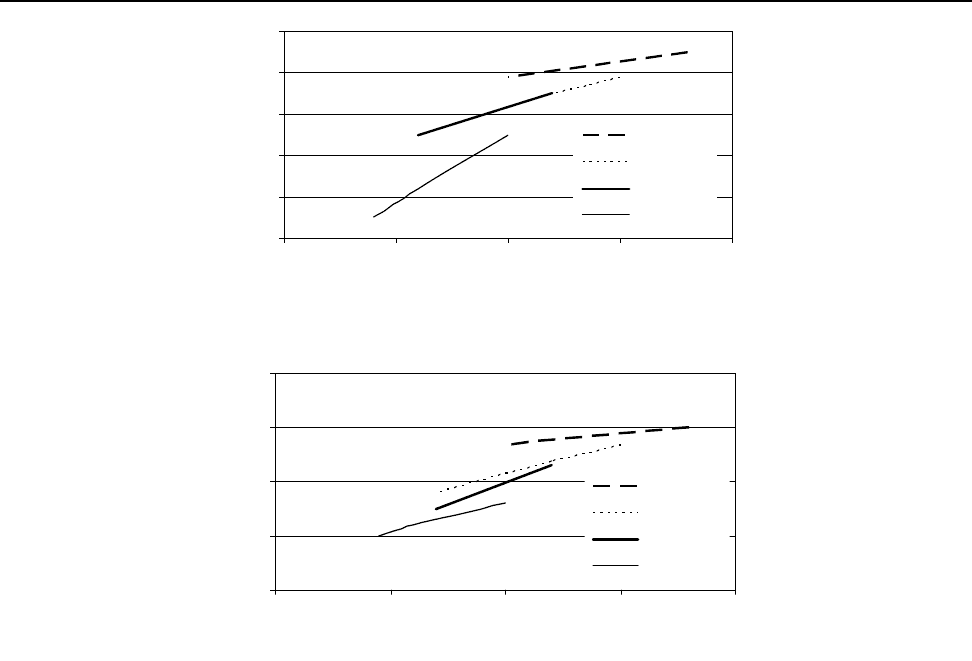
Результаты экспериментально-аналитического определения

представлены на

рисунках 2 и 3.

Анализ полученных данных свидетельствует о том, что наиболее существенно на

величину

влияет отношение

заг

dD. Влияние φ в широком диапазоне его варьирования,

определяемое изменением расстояний между осями роликов, незначительно (5…10%)

отражается на коэффициенте трения.

Это позволило с точностью не хуже 6% обобщить полученные данные и

аппроксимировать их формулой:

0816,0

0013,0f

заг

+⋅= . (4)

Возрастающая зависимость (4) в сочетании с данными [4] об уменьшении

деформации поверхностных слоёв металла с ростом

заг

dD может быть объяснена

неполным удалением окалины и связанным с этим усилением механического сцепления

заготовки с поверхностью ролика. Полученные данные свидетельствуют о значениях

коэффициента трения на контакте поверхности ролика и заготовки, которые отличаются от

принимаемых по справочным данным на 20…25%. Расчёты по методике [2] с

использованием данных настоящей работы выявили возможность уточнения на

2…3%

энергосиловых параметров волочения с поточным применением роликового

окалиноломателя.

Обработка материалов давлением №1 (19), 2008 294

0,08

0,09

0,1

0,11

0,12

0,13

0 50 100 150 200

град

D=180 мм

D=140 мм

D=100 мм

D=60 мм

Рис. 2. Зависимость коэффициента трения на контакте катанки и ролика от угла

охвата.

0,08

0,09

0,1

0,11

0,12

0 50 100 150 200

град

D=100 мм

D=80 мм

D=60 мм

D=40 мм

Рис. 3. Зависимость коэффициента трения на контакте передельной проволоки и

ролика от угла охвата.

Выводы

С использованием модернизированной схемы Эйлера трения гибкой нити на

цилиндрической поверхности выполнено экспериментально-аналитическое определение

коэффициента трения на контакте заготовки и поверхности ролика окалиноломателя. При

этом учтена упруго-пластическая составляющая силы деформирования реальной заготовки.

Показано, что основным фактором, влияющим на уровень коэффициента трения, является

отношение диаметров ролика и заготовки. Использование

данных настоящей работы

выявило возможность уточнения на 2…3% энергосиловых параметров волочения с

поточным применением роликового окалиноломателя.

ЛИТЕРАТУРА

1. Должанский А.М. Деформация катанки в роликовом окалиноломателе. Сообщение 1 /

А.М. Должанский, О.С. Ермакова // Металлургическая и горнорудная промышленность. – 2005. – №3. – С. 52-54.

2. Должанский А.М. Деформация катанки в роликовом окалиноломателе. Сообщение 2/

А.М. Должанский, О.С. Ермакова // Металлургическая и горнорудная промышленность. – 2005. – №4. – С. 51-55.

3. Брабец В.И. Проволока из цветных металлов

и сплавов: Справочник. – М.: Металлургия, 1984. – 296 с.

4. Коковихин Ю.И. Технология сталепроволочного производства. – К.: Техника, 1995. – 608 с.

Должанский А. М. – д-р техн. наук, проф. НМетАУ;

Ермакова О. С. – канд. техн. наук, доцент НМетАУ;

Ломов И. Н. –сотрудник НМетАУ;

Ломова О. Б. – сотрудник НМетАУ;

Петлёваный Е. А. – сотрудник НМетАУ.

НМетАУ – Национальная металлургическая академия Украины, г. Днепропетровск.

dmeti@dmeti.dp.ua

Обработка материалов давлением №1 (19), 2008

295

РАЗДЕЛ III

ОБОРУДОВАНИЕ И ОСНАСТКА

ОБРАБОТКИ ДАВЛЕНИЕМ

УДК 621.771.24

Антонюк Е. Я.

Бобух И. А.

Бобух В. И.

Федоренко Л. Н.

ДИНАМИЧЕСКАЯ МОДЕЛЬ ВЕРТИКАЛЬНЫХ КОЛЕБАНИЙ

ЧЕТЫРЕХВАЛКОВОЙ КЛЕТИ ПРОКАТНОГО СТАНА

Создание новых и реконструкция существующих станов связаны с большими

финансовыми затратами, значительная часть которых приходится на инжиниринговые

разработки, а также подготовку, обработку и обобщения данных о результатах

проводившихся ранее теоретических и экспериментальных исследований аналогичных видов

металлургического оборудования. Значительным резервом в деле ускорения этого цикла и

обеспечения требуемой надежности усовершенствуемых станов являются методы

математического моделирования динамических процессов с применением современных

компьютеров и их новых программных средств.

На основе работ [1–3] применительно к рабочей четырехвалковой клети с

гидравлическим нажимным устройством рассмотрены вертикальные колебания в

зависимости от технологических нагрузок. Крутильные колебания в главной линии

рассмотрены в работе [4].

Рассматривая вопрос вертикальных колебаний деталей рабочей клети в процессе

прокатки, и в частности рабочих валков, между которыми деформируется металл, к уже

сказанному выше следует добавить, что накопленный опыт экспериментальных

исследований позволил осуществить много практических внедрений в

частности, влияние

жесткости рабочей клети на геометрические параметры прокатываемой заготовки и

получение толщины готового проката. При этом вертикальная деформация клети Δi равна:

Δi =

, (1)

где Pi – сила прокатки в i проходе;

C – приведенная вертикальная жесткость рабочей клети:

∑

CiС

, (2)

где Сi – жесткости отдельных участков и деталей рабочей клети растягивающиеся и

сжимающиеся в процессе прокатки.

Однако из-за отсутствия единых требований к методике проведения эксперимента,

характеру и полноте исходной и получаемой после обработки информации не удается в

должной мере распространить результаты эксперимента на аналогичные машины близких

типов. Причиной тому

является недостаточно четкое представление об особенностях

протекающих динамических процессов в столь сложных системах таких, как рабочая клеть

прокатного стана, а также случайный характер ряда основных параметров, влияющих на

динамическую нагруженность.

Обработка материалов давлением №1 (19), 2008

296

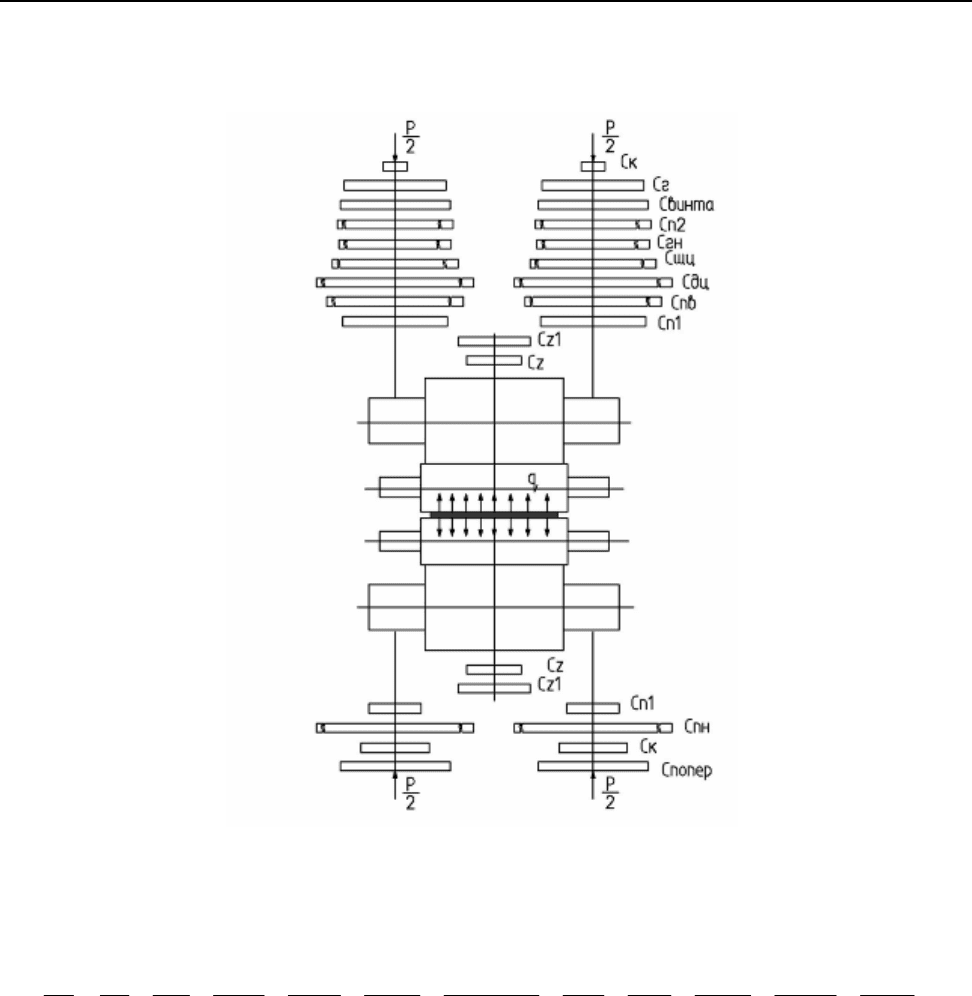
На рис. 1 приведена расчетная схема для определения вертикальных колебаний.

Расчетная схема включает элементы клети, которые в процессе нагружения или

растягиваются или сжимаются. Обозначение расчетных элементов смотри ниже в тексте.

Рис. 1. Расчетная схема для определения вертикальных колебаний.

Приведенные к вертикальным перемещениям валков жесткости Св верхней

подсистемы клети представлены зависимостями:

СпвСшцСдцСкСгСвинтаСnСгнCnСzСzСв 2

111

++++++++++= , (3)

где Cz – приведенная изгибная жесткость рабочего валка, Н/м;

Cz1 – приведенная изгибная жесткость опорного валка, Н/м;

Cn1 – радиальная жесткость подшипников опорного валка, Н/м;

Cгн – приведенная жесткость гидронажимного устройства, Н/м;

Cn2 – жесткость упорного подшипника, Н/м;

Cвинта – жесткость винта, Н/м;

Cг – жесткость нажимной гайки, Н/м;

Ск – жесткость

верхней части стоек станины, Н/м;

Сдц – приведенная к вертикальным перемещениям жесткость днища цилиндра, Н/м;

Сшц – приведенная к вертикальным перемещениям жесткость штока цилиндра, Н/м;

Спв – жесткость опорной площадки верхней подушки, Н/м.

Приведенные к вертикальным перемещениям валков жесткости Сн нижней подсистемы

клети представлены зависимостями:

Обработка материалов давлением №1 (19), 2008

297

111

СпоперСпнСкCnСzСzСн

+++++= (4)

гдеCz – приведенная изгибная жесткость рабочего валка, Н/м;

Cz1 – приведенная изгибная жесткость опорного валка, Н/м;

Cn1 – радиальная жесткость подшипников опорного валка, Н/м;

Ск – жесткость нижней части стоек станины, Н/м;

Спн – жесткость нижней опорной подушки приведенная к вертикальным

перемещениям, Н/м;

Спопер – жесткость нижней поперечины станины, Н/м.

Для

сравнения в таблице 1 приведены жесткости верхней подсистемы клети (линия 1)

и нижней подсистемы клети (линия 2) без ГНУ и с ГНУ, и жесткость клети.

Таблица 1

Приведенная податливость

Св

линии 1 без

ГНУ – 6,6605·10

-11

м/Н

Приведенная податливость

Св

линии 1

с ГНУ – 7,029·10

-11

м/Н

Приведенная податливость

Сн

линии 2 без

ГНУ – 5,071·10

-11

м/Н

Приведенная податливость

Сн

линии

2 без ГНУ – 5,071·10

-11

м/Н

Жесткость клети С:

0,852·10

Н/м (852 т/мм)

Жесткость клети С:

0,826·10

Н/м (826 т/мм)

Как видно из таблицы 1, введение дополнительных деталей при установке ГНУ

несколько снижает жесткость рабочей клети в целом с 852 т/мм до 826 т/мм. При силе

прокалки Р = 4,6·10

Н (4600 т) увеличивается деформация клети на 0,17 мм. Но благодаря

ГНУ можно предварительно сдеформировать детали клети, исключая неконтролируемую

деформацию клети, что является весьма положительным моментом применения ГНУ в

рабочих клетях.

Вместе с тем, ГНУ, как саморегулирующее устройство, является источником

колебаний. Согласно характеристике сервоклапана УП82, установленного, например, в

клетях ТЛС 2800:

при давлении 315 bar наводится

частота 75…185 Нс в зависимости от скорости

срабатывания;

при давлении 210 bar соответственно 50…150 Нс;

при давлении 140 bar соответственно 35…135 Нс.

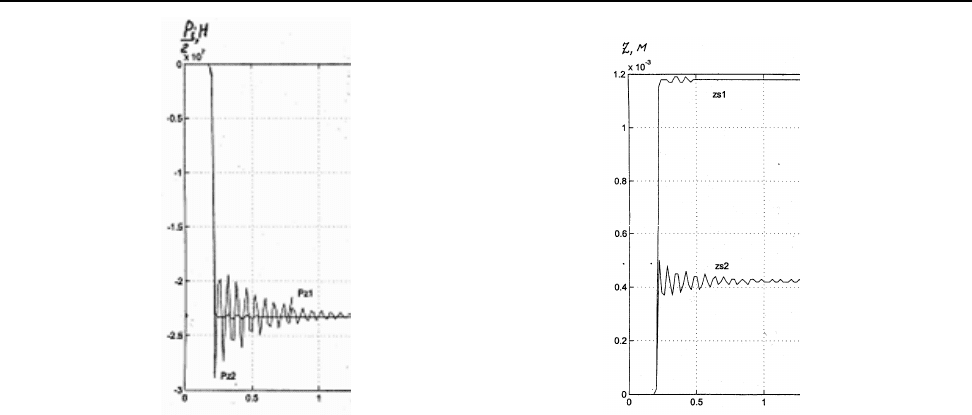
На рис. 2 показана осциллограмма вертикальных усилий при работе ГНУ,

приведенных к верхней линии клети Pz1, и нижней линии клети Pz2. Видим, что

осциллограмма Pz2 имеет ярко выраженный колебательный характер нагружения и первый

всплеск имеет максимальное значение равное 1,25 Рi,

второй всплеск 1,17 Рi, третий 1,09 Рi,

четвертый 1,13 Рi, пятый 1,06 Рi, шестой 1,08 Рi и далее с убыванием до 1 сек после захвата.

При этом частота всплесков ~30

сек

. Такую же частоту имеет осциллограмма вертикальных

усилий, отнесенная к линии верхнего валка, но амплитуда очень малая, а максимальная

величина всплеска не превышает 1,01 Рi. Согласно математической модели колебание

вертикальных усилий на верхний валок компенсируется ГНУ. Однако в реальных условиях

величины всплесков вертикальных усилий Pz1 и Pz2 следует ожидать более равномерными.

Необходимо отметить, что

моделировать вертикальные перемещения элементов

рабочей клети и вертикальные усилия реакций клети на нагружение валковой системы

довольно сложно, а в случае наличия ГНУ сложно вдвойне [5, 6] . Вертикальные усилия

реакции клети на нагружение валковой системы в случае отсутствия гидронажимного

устройства выражается зависимостью [5, 6]:

Обработка материалов давлением №1 (19), 2008

298

0, z < 0

Pzi =

-Cв z

– Hв z

, z ≥ 0 (5)

где z – перемещение;

Cв – приведенная жесткость;

Hв – коэффициент диссипативных сопротивлений при деформации.

При наличии гидронажимного устройства Pzi = Pгi, где

0, z

< 0

Pгi = - (1+А

sinw

t) C

·z

+ H

⋅

, 0 ≤ z

≤ z

(6)

·z

·(

⋅

)

sign

⋅

, z

< z

≤ z

Pm, z

< z

где C

, C

, H

, z

, А

, w

, в

– константы.

Жесткость С

рассчитывается как для последовательного соединения упругого

элемента C

с приведенным упругим элементом гидронажимного устройства Сг.

Зависимость (6) сформирована для системы с предварительным натягом. При этом на

первом этапе деформации имеет место высокая жесткость C

, которая претерпевает

скачкообразное изменение в сторону уменьшения до величины C

в момент, когда внешнее

усилие (технологическая нагрузка) достигнет величины усилия предварительного натяжения

в гидравлическом нажимном устройстве. При последующей деформации, кроме силы

упругости, определяемой приведенной жесткостью с учетом жесткости гидросистемы,

возникает также приведенная сила гидравлического сопротивления, величина которой

принимается пропорционально квадрату скорости вертикального перемещения валков [6].

Так при максимальном перемещении ГНУ (принятого

к установке) равном 40 мм

реакция клети при прокатке толщин меньше 40 мм происходит в соответствии с выражением

(6), при этом в соответствии с характеристикой управляющей аппаратурой ГНУ усилие двух

гидроцилиндров составляет:

Pm = 2 q F η , (7)

где q – давление в цилиндрах ГНУ; q = 315 bar;

F – площадь штока цилиндра; F = 9498,5 мм

;

η – кпд.

Pm = 2 ·

013,1

315

· 9498,5 · 0,98 = 5 789 115,4 кгс = 5789 тс.

В соответствии с сиcтемой автоматического управления при силе прокатки 4600 тс

давление в управляющей аппаратуре будет равно ~250 bar. Адаптация системы между

пропусками позволит, изменяя давление в управляющей аппаратуре, менять величину Pmi,

приближаясь к фактической силе прокатки.

При прокатке толщин свыше 40 мм вертикальные усилия реакции клети сначала

будут определяться

в соответствии с зависимостью (5), а при достижении в ГНУ расчетного

давления по выражению (6). Общая выравнивающая способность ГНУ по толщине подката

при этом будет ниже. Этот вывод касается и прокатки в черновой клети.

Обработка материалов давлением №1 (19), 2008

299

t, с t, c

Рис. 2. Вертикальные усилия, Рис. 3 – Вертикальные перемещения

действующие на валки. валков.

На рис. 3 показаны осциллограммы вертикальных перемещений валков. Суммарное

перемещение под нагрузкой валков нижней и верхней линии составляет 1,6 мм. Таким

образом, наличие ГНУ при пропуске с силой прокатки 4600 т значительно снижает

неконтролируемую деформацию, в нашем случае с 5,4 до 1,6 мм, т.е.

на 62,5%.

Выводы

Установка в рабочей клети прокатного стана ГНУ с точки зрения выравнивания и

получения заданной толщины с меньшими отклонениями является положительным

результатом. С другой стороны, ГНУ, как саморегулирующее устройство с высокой

собственной частотой, является источником самих колебаний, что требует определенных мер

по защите от этих колебаний.

ЛИТЕРАТУРА

1. Кожевников С.Н. Динамический синтез главных линий обжимных прокатных станов /

С.Н. Кожевников, В.К. Кулик, А.И. Ткачук // Прикл. механика.-1985.-21, №4.-С. 75-84.

2. Кожевников С.Н. Возможности повышения надежности металлургических машин /

С.Н. Кожевников, Е.Я. Антонюк, А.И. Ткачук // Динамика и прочность тяжелых машин.-1988.-Вып.15.-С. 5-4.

3. Ларин В.

Б. Проблемы динамики прокатных станов (обзор) / В.Б. Ларин, Е.Я. Антонюк, И.А. Бобух,

В.В. Веренев, С.А. Ясинский // Прикл. механика.- 1977.-33, №3.-С. 3-27.

4. Антонюк Е.Я. Математическая модель динамической нагруженности главной линии четырехвалковой

клети прокатного стана / Е.Я. Антонюк, А.И. Бобух, В.И. Бобух // Удосконалення процесів і

обладнання обробки

тиском в металургії і машинобудуванні: Зб. наук. пр.-Краматорськ:ДДМА, 2007.-С. 516-521.

5. Кожевников С.Н. Гидравлический и пневматический приводы металлургических машин./ С.Н.

Кожевников, В.Ф. Пешат - М.: Машиностроение, 1973.-360 с.

6. Башта Т.М. Машиностроительная гидравлика. – М.: Машиностроение, 1971.-672 с.

Антонюк Е. Я. – канд. техн. наук, ст. науч. сотрудник ИМех НАН Украины;

Бобух И. А. – доцент каф. АММ ДГМА;

Бобух В. И. – аспирант ДГМА;

Федоренко Л. Н. – сотрудник ЗАО «НКМЗ».

ИМех НАН Украины – Институт механики Национальной академии наук Украины, г. Киев;

ЗАО «НКМЗ» – ЗАО «Новокраматорский машиностроительный завод», г. Краматорск;

ДГМА – Донбасская

государственная машиностроительная академия, г. Краматорск.

amm@dgma.donetsk.ua

Обработка материалов давлением №1 (19), 2008

300

УДК 621.979.134

Вишневський П. С.

Добровлянський С. М.

Холявік О. В.

ЕКСПЕРИМЕНТАЛЬНА УСТАНОВКА ДЛЯ МОДЕЛЮВАННЯ ПРОЦЕСУ

ВИТЯГУВАННЯ З ЛИСТОВОГО МЕТАЛУ ПОРОЖНИСТИХ ВИРОБІВ

КОРОБЧАСТОЇ ФОРМИ

Для аналізу процесів обробки металів тиском широке застосування знайшов метод

гідродинамічних аналогій, запропонований А. А. Іллюшиним і П. М. Огібаловим, як

наближений метод розв’язку задач теорії пластичності. При цьому в першому наближенні

приймався розв’язок гідродинамічної задачі із схожими граничними умовами [1,2].

Теоретичним підґрунтям для цього служила формальна схожість зв’язку

компонентів

девіаторів напруг і швидкостей деформацій гідродинамічної задачі, напруг і приросту

компонент деформацій задачі пластичної течії [3]. Стосовно процесів обробки металів

тиском цей метод розвивався рядом провідник наукових шкіл з обробки металів тиском в

декількох напрямках.

Зокрема, ефективність його була підтверджена роботами наукової школи, яку створив

І. Я. Тарновський [4]. Використовуючи варіаційні

принципи теорії пластичності,

представниками цієї школи була розроблена методика визначення енергосилових параметрів

процесів ОМТ при гарячій деформації. Слід відзначити, що ними було експериментально

підтверджено, що при осаджуванні зразків із різних металів (свинець, мідь, алюміній) при

аналогічних контактних умовах у випадку значних пластичних деформацій, фізико-механічні

властивості матеріалу зразків практично не впливають

на кінематичні параметри процесу.

Наприклад, розширення зразків, деформованих на 30%, відрізнялось для різних металів не

більше ніж на 8%, що було в межах похибки експерименту. Для визначення компонентів

тензора деформацій, як функцій координат точок деформованого металу, а також розмірів і

форми виробу на довільному етапі деформування, переміщення задавались функціями (в які

входили

невизначені параметри), що задовольняли граничним умовам.

Невідомі параметри знаходились із умови мінімуму функціоналу повної енергії

деформації. Одержані залежності в більшості мали досить складний аналітичний вираз.

Іншим напрямком реалізації методу гідродинамічних аналогій є метод швидкостей

деформування, обґрунтований Ю. Н. Алексєєвим [5]. При цьому вихідним є поле

швидкостей точок деформованого тіла. Воно може задаватись

на основі аналізу

технологічного процесу і повинно задовольняти граничним умовам.

На контактній поверхні поле швидкостей визначається рухом інструменту і відповідні

компоненти векторів швидкостей повинні затухати від рухомої контактної поверхні

інструмента в напрямку до нерухомих.

Оскільки можна завжди підібрати необхідні аналітичні вирази для такого поля

швидкостей, то можна одержати і відповідні

функції для компонент тензора швидкостей

деформації. Обравши необхідний вираз для апроксимації зв’язку властивостей напружень і

деформацій (наприклад, у вигляді степеневої функції

εσ

⋅= ) можна визначити роботу

пластичної деформації, після чого мінімізуючи функціонал роботи, знайти більш точні

вирази для поля швидкостей і визначити параметри напруженого стану. Цей метод за своїм

змістом відноситься до методу верхньої оцінки і дозволяє одержати енергосилові параметри,

що відповідають обраному і уточненому полю швидкостей.