Новосельцева Т.А., Корепанова В.С. Метрология

Подождите немного. Документ загружается.

110

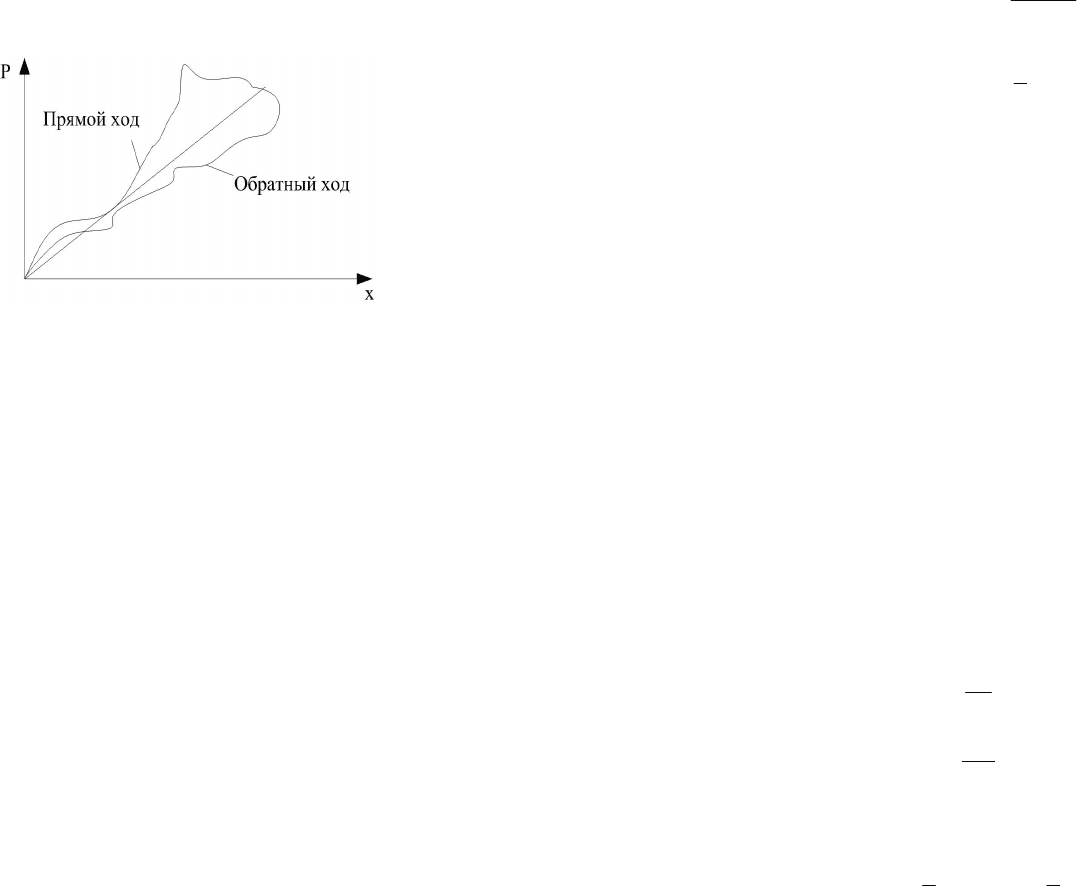
3. Проводят симметричные измерения. Например: для исключения по-

грешностей от гистерезиса проходят по шкале вверх и вниз (так называемый

«прямой» и «обратный» ход), а затем усредняют результаты (рис. 7.2).

Рисунок 7.2 — Исключение систематических погрешностей

(погрешностей от гистерезиса) с помощью симметричных измерений

Систематическая погрешность, изменяющаяся в процессе измерения и

обнаруженная статистическими методами, может быть в значительной степе-

ни скомпенсирована только в случае знания закона ее изменения (например,

зависимость от температуры). Для выяснения характера зависимости группо-

вого среднего систематической погрешности используют

регрессивный ана-

лиз, а для обнаружения связи между систематической погрешностью и изме-

ряемой физической величиной используют корреляционный анализ. Изучение

методов корреляционного анализа выходит за рамки рассматриваемых вопро-

сов, так как они достаточно сложны и для изучения требуют большего коли-

чества времени.

На практике систематическая погрешность очень часто включает в себя

несколько

составляющих, исключить (учесть) которые полностью не всегда

удается. Очень часто остаются так называемые не исключенные остатки систе-

матической погрешности или просто не исключенные систематические по-

грешности (НСП), т. е. погрешности, оставшиеся после введения поправок.

К числу не исключенных систематических погрешностей относятся:

— погрешности, связанные с точностью определения поправок;

— погрешности, зависящие

от точности измерения влияющей величины,

входящей в формулу определения поправок;

Оценка по размаху:

= .

Оценка по среднему арифметическому:

∑

На практике не всегда удается получить оценки параметров функций рас-

пределения случайной величины, удовлетворяющие всем трем требованиям:

состоятельности, несмещенности и эффективности.

Способы получения оценки зависят от закона распределения случайной

величины. Для случайных величин, распределенных по различным законам,

оценки параметров функций распределения проводят по разным формулам.

Существуют различные методы получения оценок.

Наиболее распростра-

ненным является

метод максимального правдоподобия.

Введем понятие функции правдоподобия, которая зависит от самих результа-

тов наблюдений. Если Х

результат наблюдений, то функция правдоподобия:

() ( )

xxix

qPX, Q,

σ= σ,

где

()

xi x

PX, Q,

σ — произведение.

Для упрощения вычислений пользуются логарифмической функцией

правдоподобия:

()()

12 n x x i x

L X ,X ,...,X ,Q, P X , Q,

=σ.

Оценки максимального правдоподобия получают решением системы

уравнений в частных производных:

QQ,

=σ=σ

∂

⎡⎤

⎢⎥

∂

⎣⎦

;

QQ,

=σ=σ

⎡⎤

∂

⎢⎥

∂σ

⎣⎦

Для нормального распределения случайных величин и случайных по-

грешностей оценки максимального правдоподобия:

∑

;

⎛⎞

σ= −

⎜⎟

⎝⎠

∑

где

Q — точечная оценка максимального правдоподобия.

Однако оценка дисперсии, полученная таким образом, не является не-

смещенной. Для получения несмещенной оценки дисперсии случайной по-

грешности используют формулу:

()

DS X X

== −

−

∑

, (5.58)

где

XQ= .

Тогда, оценка СКО случайной погрешности, полученная методом макси-

мального правдоподобия:

()

−

σ= =

−

∑

, (5.59)

где

∑

— несмещенная оценка генеральной средней;

— результат i-го наблюдения.

Условимся в дальнейшем обозначать оценку математического ожидания

и СКО через

X и S

иногда называют стандартом).

Для равномерного закона распределения погрешностей:

∧

= ;

∧

−

, (5.60)

где

12 in1

X , X ,..., X , X — члены упорядоченного ряда наблюдений (упорядочен-

ная выборка

ii1

≤ ).

Достоинствами метода максимального правдоподобия является то, что

полученные оценки:

— асимптотически несмещенные (при n →∞);

— асимптотически эффективные;

— асимптотически нормально распределенные.

То есть, если

∧

— оценка максимального правдоподобия параметра А,

то при достаточно большом числе наблюдений (n > 25) эта оценка может счи-

таться нормально распределенной при любом распределении результатов на-

блюдений, причем при n→∞

}

PA1

∧

⎧

⎨

⎩

, т. е. эта оценка состоятельная.

Математическое ожидание среднего арифметического значения случай-

ной величины

⎡⎤

⎣⎦

совпадает с математическим ожиданием случайной вели-

чины М[Х], т. е.

[]

MX MX

⎡⎤

⎣⎦

109

(например, времени, контролируемой температуры, давления и др.), а также

корреляционного анализа для обнаружения связи между результатами наблю-

дений и значениями измеряемой ФВ.

Таблица 7.1 — Значения параметра

табл

4 0,3902 13 0,5778

5 0,4102 14 0,5908

6 0,4451 15 0,6027

7 0,4680 16 0,6137

8 0,4912 17 0,6237

9 0,5121 18 0,6330

10 0,5311 19 0,6417

11 0,5482 20 0,6498

12 0,5636 25 0,6836

Изучение методов регрессионного и корреляционного анализа, которые

достаточно сложны, в данном учебном пособии не рассматриваются.

Естественно, что лучше сразу получать результаты измерений без систе-

матической погрешности или с небольшой погрешностью. Полностью исклю-

чить систематическую погрешность в процессе измерений не удается. Однако

существуют специальные приемы, обеспечивающие исключение части систе-

матической составляющей

погрешности измерений.

Рассмотрим основные из них.

Если систематические погрешности считаются постоянными но характе-

ру проявления, то применяют один из следующих методов.

1. Исключение самого источника систематической составляющей по-

грешности измерений. Например: путем предварительной установки измери-

тельного прибора по уровню исключают погрешность от его неуравновешен-

ной подвижной части.

2. Компенсация погрешности по знаку

. Например: погрешность исклю-

чают путем вариаций показаний прибора, определяя значение измеряемой ве-

личины при подходе к определенной точке шкалы слева и справа, а затем вы-

числяют среднее значение.

108

наружить. Анализ таких погрешностей возможен только на основании некото-

рых априорных знаний об этих погрешностях.

Прогрессирующие систематически погрешности могут быть обнаружены

с помощью построения графика последовательности неисправленных результа-

тов наблюдений или их отклонений от среднего значения (рис. 7.1).

Рисунок 7.1 — Последовательность неисправленных результатов

наблюдений или их отклонений от среднего значения:

V — отклонения неисправленных результатов наблюдений.

Систематические погрешности, изменяющиеся в процессе измерения, мо-

гут быть обнаружены аналитическими методами. Суть этих методов заключа-

ется в проверке статистической подконтрольности принятой гипотезы. Для это-

го могут быть использованы критерии Аббе или Бартлетта.

Рассмотрим сущность критерия Аббе.

После исключения грубых погрешностей определяют значение параметра

эксп

q :

()

i1 i

эксп i

q;XX

−

∑

. (7.3)

Следующим шагом проверятся условие

эксп табл

. Если это условие вы-

полняется, то систематическая погрешность присутствует. Значения параметра

табл

q представлены в таблице 7.1.

Проверка наличия систематической погрешности в ряде измерений может

быть осуществлена с помощью регрессионного анализа для выяснения характе-

ра зависимости группового среднего от некоторого неслучайного аргумента

Поскольку среднее арифметическое значение результатов измерений X

получается в результате деления суммы сложения случайных величин Xi на их

число n (

∑

), то оно также является случайной величиной с дисперси-

ей D(X). Дисперсия среднего арифметического значения определяется как:

()

(

)

(

)

in in

i1 i1

nD x D x

DX D x Dx

nn nn

⎡⎤

== ==

⎢⎥

⎣⎦

∑∑

. (5.61)

Из выражения (5.61) следует, что точность результата измерения можно

повысить путем увеличения числа измерений, поскольку дисперсия среднего

арифметического значения из n наблюдений в n раз меньше дисперсии резуль-

тата однократного наблюдения.

Среднеквадратичное отклонение среднего арифметического

σ в n раз

меньше среднеквадратичного отклонения единичного измерения

/nσ=σ .

В качестве точечной оценки дисперсии используют среднее – квадратич-

ное отклонение среднего арифметического значения случайной величины

()

∧

=−

∑

Поскольку эта оценка является смещенной, для точечной оценки средне-

квадратичного отклонения используют не среднеквадратичное отклонение ге-

неральной совокупности

∧

, а так называемое выборочное среднеквадратич-

ное отклонение S

, равное квадратному корню из эмпирической дисперсии:

()

SXX

=−

−

∑

. (5.62)

Величина S

характеризует разброс отдельных результатов измерений от-

носительно среднего арифметического значения

Оценка среднеквадратичного отклонения среднего арифметического

значения:

()

SS XX

nn(n1)

== −

−

∑

. (5.63)

Результат измерения в случае точечной оценки записывается как:

AX= ;

S ...;

n=…

Это позволяет сделать соответствующие выводы относительно точности

измерения: число измерений n = 50 характеризует надежность определения

стандарта S

, который в свою очередь характеризует близость X к истинному

значению измеряемой величины.

Пример

. Из генеральной совокупности извлечена выборка объемом n = 50.

Случайная величина Х

принимает значения: 2, 5, 7, 10; относительная частота

(частость) n

: 16, 12, 8, 14;

n50=

∑

Найти несмещенную оценку генеральной средней.

Несмещенной оценкой генеральной средней является выборочная

средняя:

16 2 12 5 8 7 14 10

X5,76

n50

⋅+ ⋅+⋅+ ⋅

== =

∑

Таким образом, несмещенная оценка генеральной средней равна 5,76.

Интервальные оценки параметров функций распределения погрешностей

или результатов наблюдений получают путем определения интервалов, в гра-

ницах которых с определенной вероятностью находятся истинные значения

оцениваемых параметров. Такой интервал называется доверительным, а соот-

ветствующая вероятность — доверительной вероятностью.

Доверительный интервал — интервал значений случайной погрешности,

внутри которого с заданной вероятностью находится искомое (истинное) зна-

чение погрешности результатов измерений. Границы доверительного интервала

называют доверительными границами — верхней и нижней.

Если результаты наблюдений или погрешность результата наблюдений

распределены по нормальному закону с известным СКО (

∆

=σ ), то довери-

тельная вероятность

нахождения истинного значения измеряемой величины Q

в доверительном интервале

px px

Xt , Xt

⎡⎤

−σ +σ

⎣⎦

определяется выражением:

(

)

{

}

(

)

px px p

PXt QXt 2Ф t1−σ < ≤ +σ = −. (5.64)

где

(

)

Ф t — нормированная интегральная функция нормального распределе-

ния, но поскольку

(

)

(

)

(

)

(

)

Ф z1Ф –z , т. е. Ф –z 1 Ф z=− =− , то:

{

}

(

)

px px p

PXt QXt 2Ф t1

−σ< ≤ +σ = −

, (5.65)

Половина доверительного интервала

называется доверительной гра-

ницей случайного отклонения результатов наблюдений, соответствующего до-

верительной вероятности

Р. Для определения доверительной границы задаются

доверительной вероятностью

Р* (например,

P0,95= или

P0,997= ).

107

ческое ожидание равно оцениваемому параметру, эффективной — если ее дис-

персия меньше любой, получаемой другим способом.

Как это было показано ранее, результаты измерения

'' '

12 i

X ,X , ..., X в об-

щем случае могут содержать систематическую

, случайную

∆ и грубую

гр

∆

погрешности. Результаты измерений, содержащие систематическую погреш-

ность, обозначают знаком «

», тогда результат измерения можно представить

как:

ii гр

X =Θ +∆+∆ . (7.2)

На первом этапе обработки результатов измерений оценивают наличие

промахов (или грубых погрешностей). Промах — случайная погрешность ре-

зультата отдельного наблюдения, которая для данных условий резко отличается

от отдельных результатов этого же ряда.

Оценка наличия грубых погрешностей решается методами математиче-

ской статистики — статистической проверкой гипотез. Суть методов заключа-

ется в

том, что выдвигается нулевая гипотеза относительно результата измере-

ния, который вызывает сомнение в его правильности и может рассматриваться

как промах в связи с большим отклонением от других результатов измерения.

Нулевая гипотеза утверждает, что «подозрительный» результат в действитель-

ности принадлежит к совокупности полученных в данных условиях результатов

измерений и что получение такого

результата вполне вероятно. Используя оп-

ределенные статистические критерии, пытаются доказать ее практическую не-

вероятность, т. е. опровергнуть нулевую гипотезу. Если это удается, сомни-

тельный результат исключается из дальнейшего рассмотрения. На практике

часто руководствуются рекомендацией: первый и последний результаты изме-

рений исключают из ряда полученных.

Для исключения грубых погрешностей используют критерии

Греббса

(Смирнова), Шарлье, Шовенэ и др.

В определенных случаях погрешность может считаться промахом, если

она превышает Зσ.

Затем проводится анализ наличия систематических погрешностей в ряде

измерений

'' '

12 i

X,X ,...,X, их обнаружение и исключение из результатов наблю-

дений. Получается исправленный ряд результатов наблюдений:

'' '

12 i

X,X ,...,X.

Постоянные систематические погрешности не влияют на значение слу-

чайных отклонений результатов наблюдений от средних значений, поэтому ни-

какая математическая обработка результатов наблюдений не позволяет их об-

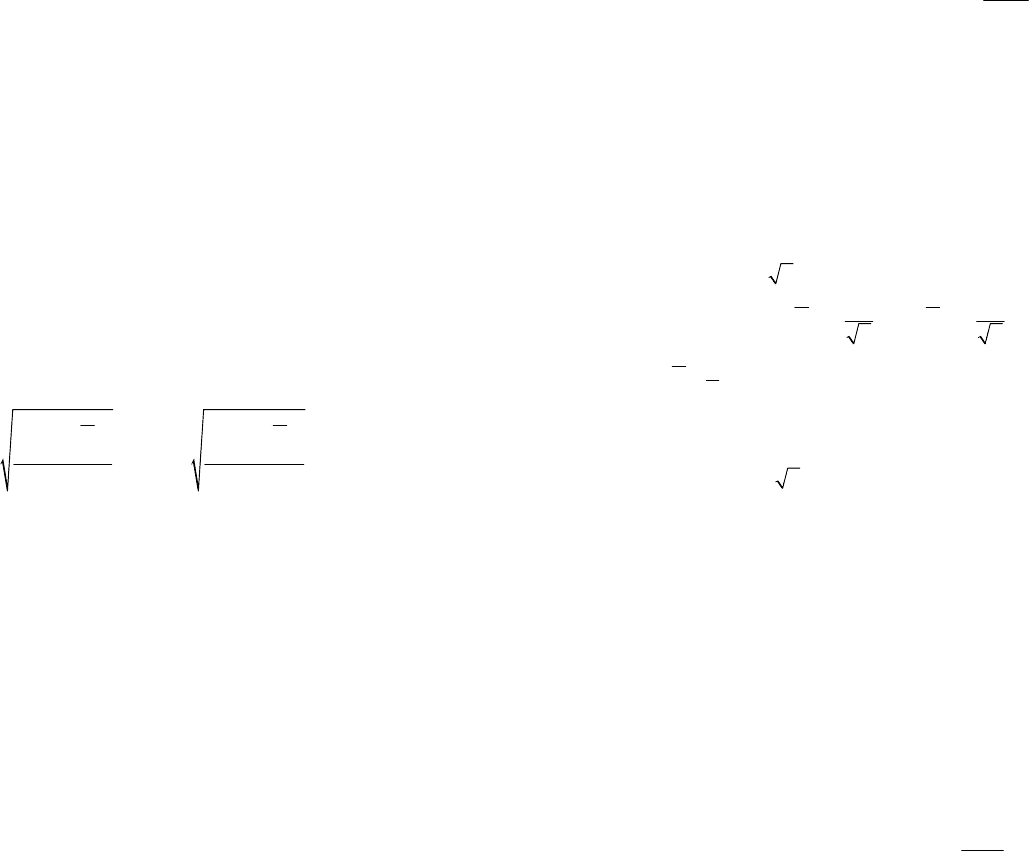
106

7 Многократные измерения и обработка их результатов

С целью повышения точности результатов измерений, т. е. снижения слу-

чайной составляющей погрешности, проводятся многократные измерения.

Как уже отмечалось выше, результаты измерений

'' ' '

12 i n

X ,X , ...X , ...X назы-

ваются равно рассеянными (равноточными), если они являются независимыми

одинаково распределенными случайными величинами.

Обработка результатов прямых равноточных наблюдений производится в

соответствии с ГОСТ 8.207-76 «ГСОЕИ. Прямые измерения с многократными

наблюдениями. Методы обработки результатов наблюдений. Основные поло-

жения».

Проверка гипотезы о равноточности (равнорассеянности) результатов

многократных измерений может проводиться с помощью различных критериев,

например, таких как критерии Фишера, Романовского и др.

С помощью критерия Фишера проверяется гипотеза о том, что два ряда,

состоящие из n

и n

результатов измерений, являются равноточными.

Сущность проверки заключается в том, что определяются эмпирические

дисперсии S

и S

для каждого ряда по формулам:

()

−

∑

()

−

∑

. (7.1)

Затем определяют дисперсионное отношение:

эксп 12

FS/S

, где

SS> .

Измерения принимаются равноточными, если значения

эксп

F не попадает в

критическую область, т. е.

эксп q

FF< .

Значения

эксп

F для различных уровней значимости q и степеней свободы

1nk

−=

1nk

−=

берутся из таблицы критерия Фишера или вычисляют-

ся по аппроксимирующим уравнениям.

Уровень значимости определяется как разница между единицей и приня-

той доверительной вероятностью: q = 1

−

р.

Конечной задачей обработки результатов любых измерений является по-

лучение оценки истинного значения измеряемой физической величины Q и по-

грешности измерения при известной доверительной вероятности.

Причем оценка должна быть состоятельной, несмещенной и эффектив-

ной. Как уже отмечалось, оценка является состоятельной, если при

∞

→n

оценка стремится к истинному значению ФВ, несмещенной — если математи-

Затем по формуле

(

)

2Ф t1P

−

= определяют значение интегральной

функции распределения для нормированного нормального распределения:

()

Ф t

= . (5.66)

Определив Ф(t

), по таблицам находят значение t

, которое зависит от

числа измерений, доверительной вероятности и степени свободы. После этого

вычисляют доверительные границы:

В px

t∆= σ и

н px

∆

=− σ ,

где индексами «В» и «Н» обозначают соответственно верхнюю и нижнюю гра-

ницы доверительного интервала.

Проведение многократных наблюдений позволяет уменьшить довери-

тельный интервал случайной погрешности, поскольку сама погрешность

уменьшается в

n раз. При n измерениях вероятность:

{

()

ppp

PX t Q X t 2Ф t1

σσ

⎫

−

<≤+ = −

⎬

⎭

, (5.67)

где

∑

— точечная оценка математического ожидания результатов на-

блюдений по числу наблюдений n.

Доверительный интервал, полученный по результатам многократных

наблюдений, в

n раз меньше интервала, вычисленного по результатам од-

нократного наблюдения измеряемой величины. На этом принципе основан

метод снижения случайных погрешностей измерений, т. е. повышения точ-

ности результатов измерений. В принципе увеличением числа наблюдений

можно получить сколь угодно малое значение случайной погрешности из-

мерений. Однако на практике это весьма сложно (а иногда

просто невоз-

можно) сделать из-за значительного увеличения времени на проведение из-

мерений. Особенно сложно это выполнить в быстро изменяющихся процес-

сах, поэтому необходимо выбирать минимально необходимое число наблю-

дений для обеспечения такой случайной погрешности, которая была бы не

больше допустимой, т. е.

ДОП

∆<∆ . Число n для нормального закона можно

определить из выражения:

ДОП

≥

∆

. (5.68)

100

Рассмотрим случай, когда распределение результатов наблюдений со-

ответствует нормальному закону, а дисперсия случайной погрешности

неизвестна. Это наиболее часто встречающийся случай и для него использу-

ют выражение:

[

]

xx x

xMx

XQ XQ

SS S

−

===,

где S

— несмещенная точечная оценка СКО; X — точечная (средняя арифме-

тическая) оценка математического ожидания результатов наблюдений.

Плотность распределения этой дроби описывается дифференциальной

функцией распределения Стьюдента:

{

()

PX Q t 2St,kdt

⎫

−< =

⎬

⎭

∫

, (5.69)

где

S(t, k) — функция распределения Стьюдента; к — число степеней свободы.

Для одной группы измерений к = (n

−

1), для j групп по n измерений в

каждой группе

k = j(n − 1). При интерполяции экспериментальных данных ли-

нейной зависимостью

у=ах+b по n точкам к = (n

−

2), при интерполяции квад-

ратичной зависимостью у = ах

+ bх + с по n точкам к = (n

−

3).

Значения t

приводятся в соответствующих справочниках и ГОСТ 8.207.

Коэффициент t

называется коэффициентом Стьюдента. В этом случае довери-

тельные границы оценки математического ожидания результатов наблюдения

определяют по формулам:

∆= ;

∆=− .

Таким образом, при интервальной оценке результат не может быть вы-

ражен одним числом. В процессе измерений получают лишь среднее значе-

ние измеряемой величины и границы доверительного интервала, внутри ко-

торого находится эта измеряемая величина с принятой доверительной веро-

ятностью. Можно сказать, что получают какую-то полосу, внутри которой

находятся возможные

значения измеряемой величины. Эту полосу называют

дорожкой погрешности возможных значений Q физической величины с оп-

ределенной вероятностью.

Пример. Найдем доверительный интервал для оценки с доверительной

вероятностью (надежностью)

Р = 0,95 неизвестного математического ожидания

параметра А нормально распределенной случайной величины

X генеральной

совокупности, если даны генеральное среднеквадратичное отклонение

= ,

выборочная средняя

X14=

и объем выборки n = 25.

105

()

p/2

S(x)

∆

∑

, (6.9)

где Z

P/2

— значения функции Лапласа.

Затем вычисляют

()

P∆ по формуле (6.6).

5. Если результат измерения включает в себя систематическую и случай-

ную погрешности, рекомендуется поступать следующим образом:

а) если отношение

8,0

, то систематической погрешностью Θ пре-

небрегают, и доверительные границы суммарной погрешности принимают рав-

ными доверительным границам случайной составляющей погрешности,

tS∆=∆=m ;

б) если отношение

0,8

> , то пренебрегают случайной составляющей

погрешности, и доверительные границы суммарной погрешности принимают

равными доверительным границам не исключенной систематической погреш-

ности

∆= Θm

;

в) если отношение лежит в интервале

0,8 8

< , то доверительные границы

погрешности результата измерения находят путем построения композиции рас-

пределения случайных и не исключенных систематических погрешностей, рас-

сматриваемых как случайные величины. В этом случае суммарная погрешность

определяется как

∆

=γ

, где

∆

+Θ

γ=

— эмпирический коэффициент,

∑

;

22 2 2

SSS S

ΣΘ

=+=+Θ

∑

. (6.10)

104

При доверительной вероятности Р от 0,9 до 0,99 оно берется из соответ-

ствующих таблиц или вычисляется по формуле:

p/2

0,490593052 0,48122493P

1 0,75082783P 75385248P

−

−+

. (6.5)

2. Если в технической документации на средство измерения или в МВИ

составляющие случайной погрешности представлены доверительными грани-

цами

(

)

P∆ при одной и той же доверительной вероятности, то доверительную

границу случайной суммарной погрешности результата измерения с однократ-

ным наблюдением при принятой доверительной вероятности P определяют по

формуле:

∆(P) ∆ (P)

∑

. (6.6)

3. Если составляющие случайной погрешности наблюдения определяют

экспериментально предварительно при тех же условиях, при котором затем вы-

полняется измерение при числе наблюдений 30n

, принимается нормальный

закон распределения случайной суммарной погрешности, а

(

)

P∆ вычисляется

по формуле:

(P) S (x)

∆=

∑

, (6.7)

где t — коэффициент Стьюдента, соответствующий наименьшему числу на-

блюдений;

()

— оценка среднеквадратичных отклонений составляющих случайной

погрешности, определяемых по формуле:

()

S(x)

−

∑

. (6.8)

Если в эксперименте нецелесообразно или невозможно определять сред-

неквадратичное составляющих случайной погрешности, а есть возможность

определить сразу суммарную случайную погрешность, то в формуле (6.8) при-

нимается n = 2.

4. Если составляющие случайной погрешности результата наблюдений

представлены доверительными границами

(

)

∆

, соответствующими различ-

ным значениям доверительной вероятности

сначала определяют среднеквад-

ратичное отклонение результата измерения с однократным наблюдением по

формуле:

101

1. Определим доверительный интервал, в котором находится значение

параметра

А с заданной доверительной вероятностью (Р = 0,95):

Xt AXt

−<<+.

Кроме значения t, все величины даны.

2. Определим t

по таблице значений функции Лапласа:

(

)

2Ф t0,95= ;

(

)

Ф t0,475= (в таблице Ф(x) и x),

t1,96

3. Подставив значение t

, получим:

14 1,96 A 14 1,96

25 25

−<<+

Если 12,04 < А <15,96 при Р = 0,95; t

= 1,96 или при Р = 0,99; t

= 2,564.

102

6 Однократные измерения и обработка их результатов

Большинство измерений в науке и технике представляют собой одно-

кратные измерения. К ним относятся и такие измерения, при которых для полу-

чения результата в одной точке проводят до пяти наблюдений. Увеличением

числа измерений (если это целесообразно и возможно) достигают более надеж-

ной информации.

Если есть возможность провести предварительные многократные измере-

ния, то это следует сделать.

Однократные измерения выполняют по следующему алгоритму:

iii

где

A — результат i-го наблюдения;

X — значение i-го показания;

Θ — поправка i-го измерения.

Необходимо отметить, что поправка определяется из априорной инфор-

мации. В первую очередь, к ней относится информация о метрологических ха-

рактеристиках средств измерений (класс точности, основная и дополнительная

погрешности и др.). Кроме того, используется информация об аналогичных из-

мерениях, проводимых раньше применяемым методом (законы распределения

измеряемой величины и

погрешности ее измерения и т. п.).

Оценка погрешности результата однократного измерения должна прово-

диться при разработке методики выполнения измерения (МВИ) и подтвер-

ждаться при ее аттестации. Если используют гостированную МВИ, то эта оцен-

ка берется из применяемого стандарта.

Обычно при оценке погрешности результата однократного измерения

принимают значение доверительной вероятности Р = 0,95.

При особо ответст-

венных измерениях значение доверительной вероятности должно быть увели-

чено до необходимой величины.

Если возможности выполнения предварительных многократных измере-

ний нет, то поступают следующим образом. В качестве результата однократно-

го измерения берется результат однократного наблюдения с введением поправ-

ки и использованием предварительно полученных данных об источниках, вы-

зывающих погрешности

измерения.

Доверительные границы не исключенной систематической погрешности

результата измерения

НСП

при принятой доверительной вероятности Р опре-

деляют по формуле:

103

НСП i

(Р) к(Р)

Θ= Θ

∑

, (6.1)

где к(Р) — коэффициент, зависящий от принятой доверительной вероятности и

числа не исключенных систематических погрешностей m;

Θ — найденные нестатистическими методами границы i-й составляющей

не исключенного остатка систематической погрешности.

При Р = 0,9к(Р) = 0,95; при Р = 0,95к(Р) = 1,1 при любом числе слагаемых m.

Значения коэффициента к(Р) от числа не исключенных систематических

погрешностей m:

m >5 4 3 2;

к(Р) 1,45 1,4 1,3 1,2.

Если не исключенные остатки систематической погрешности распределе-

ны равномерно и заданы доверительными границами

(P )

, то доверительную

границу результата измерения вычисляют следующим образом:

(P )

(Р) к(Р)

k(P)

Θ=

∑

, (6.2)

где к(Р) и к(Р

) — те же коэффициенты, что и в формуле (6.1), соответствующие

доверительной вероятности Р и P

; т — число не исключенных систематических

погрешностей.

Среднеквадратичное отклонение результата однократного измерения вы-

числяют одним из способов в зависимости от заданных условий.

1. Если в технической документации на средство измерения или в МВИ

представлены число составляющих случайной погрешности, значения средне-

квадратичных отклонений каждой погрешности и указано, что составляющие

случайной погрешности (инструментальная, методическая

, из-за влияющих

факторов и др.) распределены по нормальному закону, то среднеквадратичное

отклонение суммарной погрешности определяют по формуле:

S(X) S (X)

∑

, (6.3)

где m — число составляющих случайной погрешности;

S — значения среднеквадратичного отклонения каждой составляющей.

Доверительную границу случайной суммарной погрешности результата

измерения

()

P∆ находят по формуле:

)x(SZ)P(

2/p

∆

, (6.4)

где Z

P/2

— значение нормированной функции Лапласа в точке p/2.

117

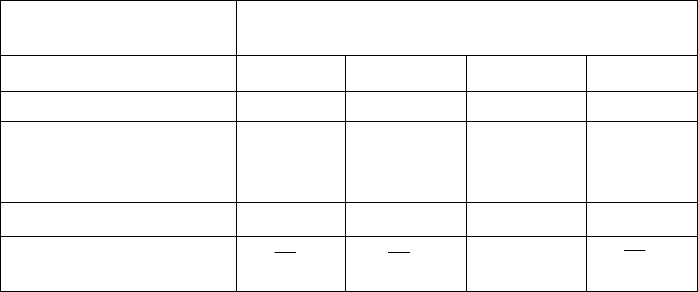
Номер измерения

в группе (i от 1 до n)

Номер группы

(j от 1 до m)

()

X ………………………

()

(

)

….

()

(

)

…

()

…

()

(

)

…

()

Средние арифметические

значения в группах

)X(

…

)X(

При этом необходимо найти наиболее достоверное значение ФВ и оце-

нить его отклонение от истинного значения.

Группы результатов наблюдений называют

неравноточными (неравно

рассеянными), если оценки их дисперсий значительно отличаются друг от дру-

га, а средние арифметические значения групп являются оценкой одного и того

же значения измеряемой ФВ.

118

8 Выбор средств измерений по точности

Погрешности средств измерений могут выражаться:

— в виде абсолютной погрешности

∆

для меры

нд

XX,

∆

=− (8.1)

где

X — номинальное значение;

X — действительное значение измеряемой величины;

для прибора

пд

XX,

∆

=−

(8.2)

где

X — показание прибора;

— в виде относительной погрешности:

(

)

/ X 100%,δ= ∆ ⋅ (8.3)

где

X — нормирующее значение измеряемой физической величины.

В качестве нормирующего значения может быть принят предел измере-

ния данными СИ, например: для весов с пределом измерения массы 10 кг

X10кг=

Если в качестве нормирующей величины принимается размах всей шка-

лы, то именно к значению этого размаха в единицах измеряемой физической

величины и относят абсолютную погрешность, например: для амперметра с

пределами от минус 100 мА до 100 мА

X = 200 мА.

Если в качестве нормирующей величины принимается длина шкалы при-

бора 1, то

X = 1.

На каждое СИ погрешность приводится только в одном виде.

Если погрешность СИ при неизменных внешних условиях постоянна во

всем диапазоне измерений, то:

∆

=± . (8.4)

Если она меняется в указанном диапазоне, то:

(

)

abx∆=± + . (8.5)

При a∆=± погрешность называется

аддитивной, а при

(

)

abx∆=± + —

мультипликативной.

Для аддитивной погрешности:

=± . (8.6)

Для мультипликативной погрешности:

cd 1

⎡

⎤

⎛⎞

δ=± + −

⎢

⎥

⎜⎟

⎢

⎥

⎝⎠

⎣

⎦

. (8.7)

Учебное издание

Новосельцева Татьяна Андреевна

Корепанова Вероника Сергеевна

МЕТРОЛОГИЯ

Учебное пособие

Редактор Л. А. Кокшарова

Технический редактор Л. П. Коровкина

План 2010 г., позиция 33. Подписано в печать 25.03.2010 г.

Компьютерный набор. Гарнитура Times New Roman.

Формат 60х84 1/16. Бумага офсетная. Печать трафаретная.

Усл. печ. л. 8,3. Уч. – изд. л. 7,9. Тираж 150 экз. Заказ № 240.

Ухтинский государственный технический университет.

169300, Республика Коми, г. Ухта, ул. Первомайская, д. 13.

Отдел

оперативной полиграфии УГТУ.

169300, Республика Коми, г. Ухта, ул. Октябрьская, д. 13.