Новосельцева Т.А., Корепанова В.С. Метрология
Подождите немного. Документ загружается.

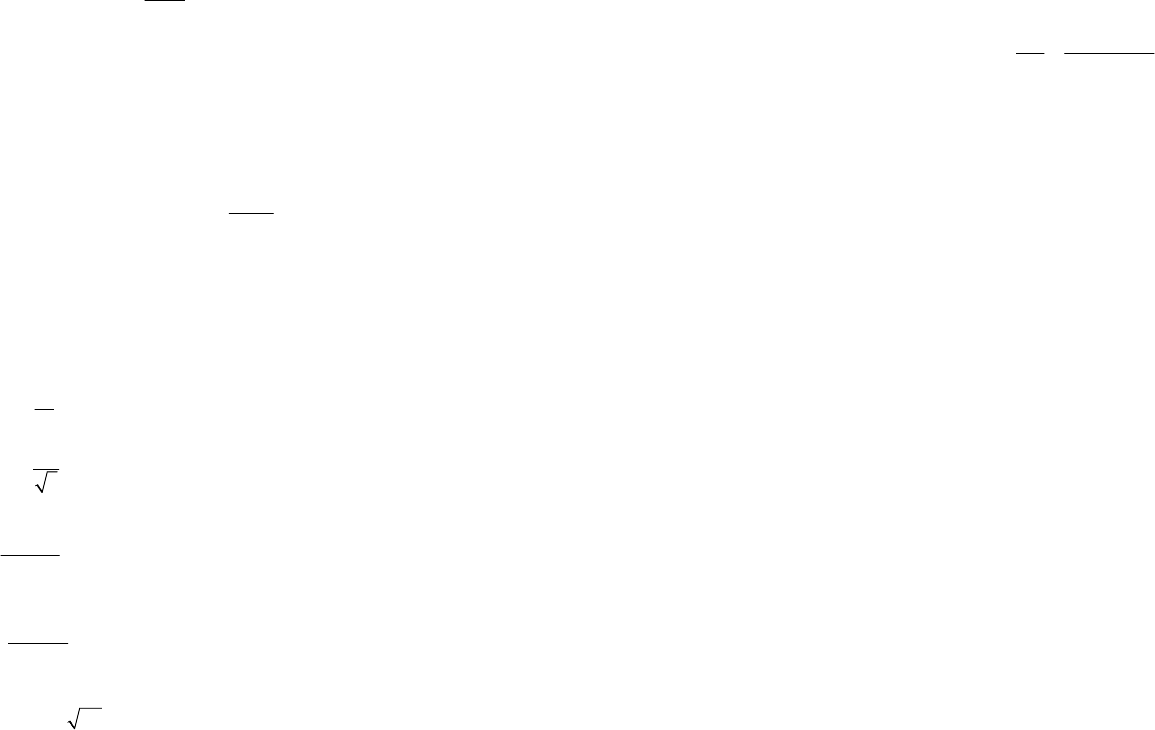
88
Область определения плотности вероятности или дифференциальной
функции равномерного распределения:
x
0, если Xa;
1
P,если aXb;
ba
0, если bX .
−
∞< <
⎧
⎪
⎪
=≤<
⎨
−
⎪
<
<+∞
⎪
⎩
(5.44)
Интегральная функция равномерного закона распределения для aXb
≤
≤
имеет вид:
()
0 при Xa;
FX
0 при Xb.
<
⎧
=
⎨
>
⎩
() ()
xx
xx
ab
Xa
PXdx PXdx при aXb
ba
−
== ≤≤
−
∫∫
. (5.45)
Числовые характеристики моментов равномерного распределения слу-
чайной погрешности
0
∆
следующие:
0
M0
⎡⎤
=
⎢⎥
⎣⎦
∆
— математическое ожидание; (5.46)
3
0
a
D
3
⎡⎤
=
⎢⎥
⎣⎦
∆
— дисперсия; (5.47)
0
a
3
⎛⎞
σ=
⎜⎟
⎝⎠
∆
— среднеквадратичное отклонение; (5.48)
0
3
k
3
0
∆
⎡⎤
µ
⎢⎥
⎣⎦
ρ= =
σ
∆
— коэффициент асимметрии; (5.49)
0
4
x
4
E31,2
∆
⎡⎤
µ
⎢⎥
⎣⎦
=−=−
σ
∆
— эксцесс. (5.50)
Практически предельное поле рассеяния при равномерном распределении
равно b — а, т. е.
23σ .
График интегральной функции равномерного распределения представлен
на рисунок 5.25.
61
или может быть выражена в процентах. В отдельных случаях может использо-
ваться приведенная погрешность — отношение абсолютной погрешности к
максимальному значению ФВ, которое может быть измерено данным средст-
вом измерения (например, верхний предел шкалы прибора).
Относительная погрешность определяется выражением:
д
дизм
д
X
XX
X
∆
δ
−
== , (5.3)
где
д
X
— действительное значение ФВ;
изм
X — результат измерения.
Поскольку
измд
XX ≅
, то принимается
изм
X/
∆
=
δ
.
5.1 Систематические погрешности
Систематические погрешности являются постоянными или закономерно
изменяются. По характеру проявления они могут быть постоянными, прогрес-
сирующими и периодическими.
Постоянные систематические погрешности — погрешности, которые не
изменяются в течение всего времени выполнения измерения. Такие погрешно-
сти возникают, например, при негоризонтальной установке рычажных весов,
погрешности градуировки средства измерения (включая неточность установки
нулевого деления), погрешности изготовления концевых мер длины и т. п.
Монотонные погрешности — погрешности, которые изменяются (убы-
вают или возрастают) монотонно. К таким погрешностям относятся погрешно-
сти, связанные с изменением длины вследствие монотонного изменения темпе-
ратуры из-за износа контактирующих в процессе измерения поверхностей или
изменения напряжения.
Периодические погрешности — погрешности, значения которых являют-
ся периодической функцией времени или функцией перемещения указателя
средства измерения. Такой погрешностью является погрешность показания ин-
дикатора, у которого ось стрелки смещена относительно центра шкалы.
Периодические погрешности могут изменяться по различным и достаточ-
но сложным законам вследствие одновременного воздействия нескольких фак-
торов, каждый из которых меняется
по своему закону.
Систематические погрешности могут возникать также вследствие инст-
рументальных погрешностей средств измерения.
Инструментальные погрешности — погрешности, причиной которых
являются свойства применяемых средств измерения. К ним можно отнести по-

62
грешности, возникающие вследствие трения, износа, наличия зазоров между
смежными деталями средств измерения, а также неточности их изготовления.
Например, для равноплечих весов нельзя изготовить идеально одинаковые пле-
чи, поэтому заведомо имеет место инструментальная погрешность.
Инструментальная погрешность может возникнуть, если между измеряе-
мой физической величиной или процессом измерения и принципом действия
средств измерения
не установлена зависимость, что может стать причиной воз-
никновения систематической
погрешности метода измерения (теоретическая
погрешность). Погрешности метода измерения могут возникать вследствие уп-
рощения или допущений при использовании эмпирических зависимостей.
Для получения достоверной измерительной информации систематические
погрешности должны быть устранены или должна быть введена соответствую-
щая поправка.
Существует несколько способов исключения систематических погрешно-
стей, которые условно можно разделить на четыре группы:
1) устранение источников погрешностей
до начала проведения измерений;
2) исключение погрешностей в процессе измерений путем замещения, ком-
пенсации, противопоставления, а также используя симметричные наблюдения;
3) внесение поправок в результат измерения;
4) определение границ доверительного интервала неисключённых систе-
матических погрешностей (НСП).
Результаты измерений, содержащие систематическую погрешность, назы-
вают неисправленными и обозначаются верхним индексом «
/
», например,
'
изм
X.
5.2 Случайные погрешности
В отличие от систематической погрешности при появлении случайной
погрешности в ее величине и знаке отсутствует закономерность. Закономер-
ность наблюдается только в распределении случайных погрешностей при про-
ведении повторных измерений.
Случайные погрешности
неизбежны и неустранимы и всегда присутст-
вуют при выполнении измерений, обусловливая рассеяние результатов при
многократных измерениях одной той же величины при неизменных условиях
измерения. Каждая случайная погрешность является следствием воздействия
многих факторов, ни один из которых не является превалирующим. Природа и
проявление случайных погрешностей различны.
87
Положим, что 3δ= σ, тогда:
(
)
(
)
PX 3 2Ф 3 2 0,49865 0,9973<δ < σ= = ⋅ = .
Таким образом, вероятность отклонения истинного значения случайной
величины
X по абсолютному значению меньше утроенного значения средне-
квадратичного отклонения и будет равна 0,9973. Это и есть
правило трех сигм,
которое формулируется следующим образом: если случайная величина распре-
делена нормально, то абсолютная величина ее максимального отклонения от
математического ожидания не превосходит утроенного среднеквадратичного
отклонения.
Другими словами: если распределение случайной величины неизвестно,
но условие, указанное в правиле трех сигм соблюдается, то есть основание
предполагать, что изучаемая случайная величина распределена нормально, в
противном случае — нет.
5.7 Равномерный закон распределения
Равномерным распределением называют такое распределение случайной
величины, при котором она может принимать любое значение в заданных пре-
делах с одинаковой вероятностью.
Дифференциальная функция равномерного распределения случайной ве-
личины (плотность вероятности) представлена на рисунке 5.24. Параметры
а и
в определяют пределы изменения случайной величины X.
Рисунок 5.24 — Дифференциальная функция равномерного
распределения случайной величины (плотность вероятности)

86
Рисунок 5.23 — Интегральная функция нормального распределения
Интегральная функция нормального распределения, представленная на
рисунок 5.23, можно выразить через дифференциальную:
() ()
()
2
2
xx
xx
2
x
1
FX p xdx e dx
2
−
−
σ
−∞ −∞
==
σπ
∫∫
. (5.42)
Правило трех сигм. На практике достаточно часто требуется оценить ве-
роятность того, что отклонение нормально распределенной величины Х по аб-
солютному значению не превышает определенный размер, который обычно
принимается равным положительному числу
δ
. Другими словами, требуется
найти вероятность того, что осуществляется неравенство | X
− а |< δ.
Это неравенство равносильно выражениям:
−
δ< X
−
а <
δ
или (а
−
δ
) < Х< (а +
δ
).
Используя правило, что вероятность попадания нормально распределен-
ной случайной величины в заданный интервал равна разнице значений функции
Лапласа на границах этого интервала, т. е.:
()()
Р XfxdxФ 2Ф
β
α
β−α
⎛⎞
α< <β = = =
⎜⎟
σ
⎝⎠
∫
,
получим:
(
)
(
)
(
)
()
()
()
()
Р Xa Pa X a
aa aa
ФФФФ2Ф .
−<δ= −δ< < +δ=
⎡⎤⎡⎤
+δ − −δ −
δ
δδ
⎛⎞ ⎛ ⎞ ⎛⎞
=−=−−=
⎢⎥⎢⎥
⎜⎟ ⎜ ⎟ ⎜⎟
σσσσσ
⎝⎠ ⎝ ⎠ ⎝⎠
⎢⎥⎢⎥
⎣⎦⎣⎦
(5.43)
При a0=
PX a 2Ф
δ
⎛⎞
−<δ=
⎜⎟
σ
⎝⎠
.
63
Поскольку случайные погрешности не поддаются исключению из резуль-
татов измерений, то в измерительную задачу входит определение их влияния на
результат измерений.
Для определения и учета случайных погрешностей используют методы
теории вероятностей и математической статистики, которые также применяют
и при не исключенных систематических погрешностях.
Случайная погрешность обозначается верхним индексом «0» и является
случайной функцией времени
()
τ∆=∆
00
, которая отличается тем, что нельзя ска-
зать какое значение она может принять в некоторый момент времени (рис. 5.1)
Рисунок 5.1 — Изменение случайной погрешности во времени
Суммарная погрешность измерения
i
∆
, соответствующая каждому зна-
чению времени
i
τ , включает в себя систематическую
i
Θ
и случайную
0
∆
со-
ставляющие:
0
ii
∆+Θ=∆ . (5.4)
Погрешность измерения, соответствующая каждому значению времени
j
τ , называется сечением случайной функции
(
)
τ
∆
или погрешностью наблюде-
ния измеряемой ФВ в момент времени
j
τ
.
Если систематическая погрешность учитывает тенденцию изменения по-
грешности во времени, то как определить случайную погрешность?
Предположим, что:
()
0
i
=
τΘ , при
m
....,1i
=
, т. е. систематическую по-
грешность удалось полностью исключить из результатов измерений. Значения
64
же случайной погрешности в каждом сечении не зависят друг от друга, т. е.
знание случайной погрешности в одном сечении не дает никакой информации о
погрешности в другом сечении. Тогда случайная погрешность может рассмат-
риваться как случайная величина, а сами результаты наблюдения ФВ в каждый
момент времени
j
τ являются независимыми случайными величинами. В этих
условиях случайная погрешность наблюдения
0
∆
определяет как разность меж-
ду исправленным результатом наблюдения X и истинным значением измеряе-
мой величины:
QX
0
−=∆ .
Исправленный результат наблюдений — результат наблюдений, из кото-
рого исключена систематическая погрешность.
Наблюдение — совокупность операций при измерении, имеющих своей
целью своевременное и правильное выполнение отсчета.
С другой стороны, наблюдение — экспериментальная операция, выпол-
няемая в процессе измерений, в результате которой получают одно значение из
группы значений величины, подлежащих обработке для получения результата
измерений. Например, если по трем или пяти наблюдениям получают один ре-
зультат,
то можно считать, что результат наблюдений дает один результат из-
мерения, а тот в свою очередь — значение измеряемой ФВ, найденное путем
обработки результатов наблюдений.
Как правило, для уменьшения случайной погрешности и исключения
промахов измерения проводят с многократными наблюдениями. Обработка ре-
зультатов наблюдений проводится методами математической статистики по
правилам случайных величин.
5.3 Случайные величины
Измеряемые величины могут быть детерминированными (определенны-
ми) и случайными. Случайные величины могут быть дискретными и непрерыв-
ными.
Дискретной величиной называется случайная величина, которая прини-
мает изолированные возможные значения с определенной вероятностью. От-
дельные значения такой величины могут быть пронумерованы, например, дис-
кретными величинами являются: число деталей, число измерений и т.
д. Дис-
кретная величина не может иметь промежуточного значения.
85
Рисунок 5.22 – Определение вероятности попадания результата
наблюдения в заданный интервал
В теории вероятности и метрологии для определения вероятности попа-
дания наблюдений в некоторый интервал применяется нормированная функция
Лапласа:
()
z
2
1t
Ф Z exp dt
2
2
−∞
⎛⎞
=−
⎜⎟
π
⎝⎠
∫
,
которая табулирована (таблицы приведены в справочниках теории вероятности
и метрологии). Используя функцию Лапласа, можно определить вероятность
попадания результата наблюдения Х в интервал (х
1
, х
2
):
{}()()
21
1221
xx
xQ xQ
Px X x Ф t Ф t ФФ
⎛⎞⎛⎞
−−
<≤ = − = −
⎜⎟⎜⎟
σσ
⎝⎠⎝⎠
. (5.40)
Данное выражение указывает на то, что вероятность попадания результа-
та наблюдения в заданный интервал
[
]
12
x,x равна разнице значений функции
Лапласа в точках верхней и нижней границ доверительного интервала.
При рассмотрении формулы (5.40) следует иметь в виду, что:
(
)
(
)
Ф Z1Ф Z
−
=− .
Моменты функции распределения случайной погрешности
0
∆ , распреде-
ленной по нормальному закону, имеют вид:
0
x
Mm0
⎡⎤
∆= =
⎢⎥
⎣⎦
;
0
22
D
∆
⎡⎤
∆
=σ =σ
⎢⎥
⎣⎦
;
0
3
k
3
0
∆
⎡⎤
µ∆
⎢⎥
⎣⎦
ρ= =
σ
;
0
4
x
4
E30
∆
⎡⎤
µ∆
⎢⎥
⎣⎦
=
−=
σ
. (5.41)
84
Рисунок 5.20 – Дифференциальная функция нормального распределения
(кривая Гаусса)
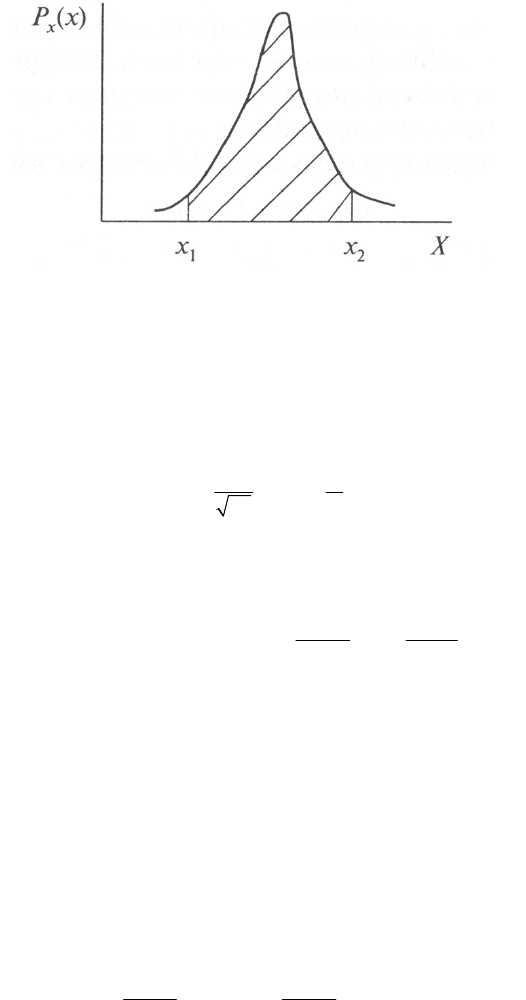
Рисунок 5.21 – Зависимость случайной погрешности
0
∆ со
среднеквадратичным отклонением
∆
σ
Положение кривой
(
)
(
)
x
Px fx
=
относительно начала координат опреде-
ляется значением математического ожидания. Причем, как правило, берется не
математическое ожидание, а среднее арифметическое значение результатов
многократных наблюдений
X .
Форма кривой нормального распределения определяется параметром а.
Как было показано ранее, чем меньше а, тем более островершинной становится
кривая, а ее ветви сближаются (рис. 5.22).
Вероятность попадания результата наблюдения в заданный интервал [х
1
, х
2
]
равна площади под кривой нормального распределения, ограниченной нижней х
1
и верхней х
2
границами доверительного интервала (рис. 5.22).
65
Непрерывной величиной называется случайная величина, которая может
принимать все значения в некотором конечном или бесконечном промежутке.
Число возможных значений непрерывной случайной величины бесконечно, на-
пример, отклонение размера изготовленной детали от номинального значения,
погрешность измерения и т. п.
Случайная величина не может характеризоваться одним числом, для нее
обязательно должно быть указано множество
возможных значений и вероятно-
стные характеристики ее появления, заданные в указанном множестве. В тео-
рии вероятностей событие, которое может произойти или не произойти, назы-
вается случайным.
Количественной оценкой возможности появления данного случайного
события является его вероятность Р. Если имеется всего n событий, a m — чис-
ло возможных событий, то вероятность появления возможного события: P=m/n.
Невозможному событию соответствует вероятность 0, а возможному —
соответствует 1.
Дискретные случайные величины x
k
полностью характеризуются вероят-
ностями своих отдельных значений P
k
: P
k
:P(X = x
k
); k=1,2,..., n причем X = x
k
является случайным событием. Поскольку данное равенство содержит полную
группу событий, то сумма всех событий P
k
равна 1:
n
k
k1
P1
=
=
∑
.
Описанием вероятности случайной величины является закон ее распреде-
ления. Законом распределения случайной величины называется функция, уста-
навливающая связь между возможными значениями случайной величины и со-
ответствующими им вероятностями. Закон распределения может быть задан в
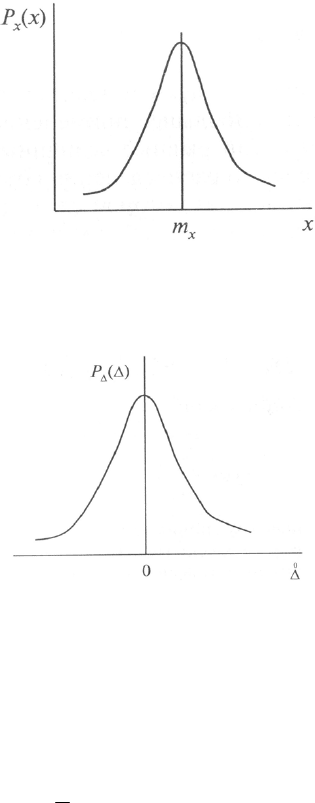
различной форме: таблицей, графиком, зависимостью. Графическое представ-
ление ряда распределения случайной величины называется полигоном распре-
деления
(рис. 5.2).
Интегральная функция распределения случайной дискретной величины
представлена на рисунке 5.3.
Интегральная функция распределения случайной непрерывной величины
представлена на рисунке 5.4.
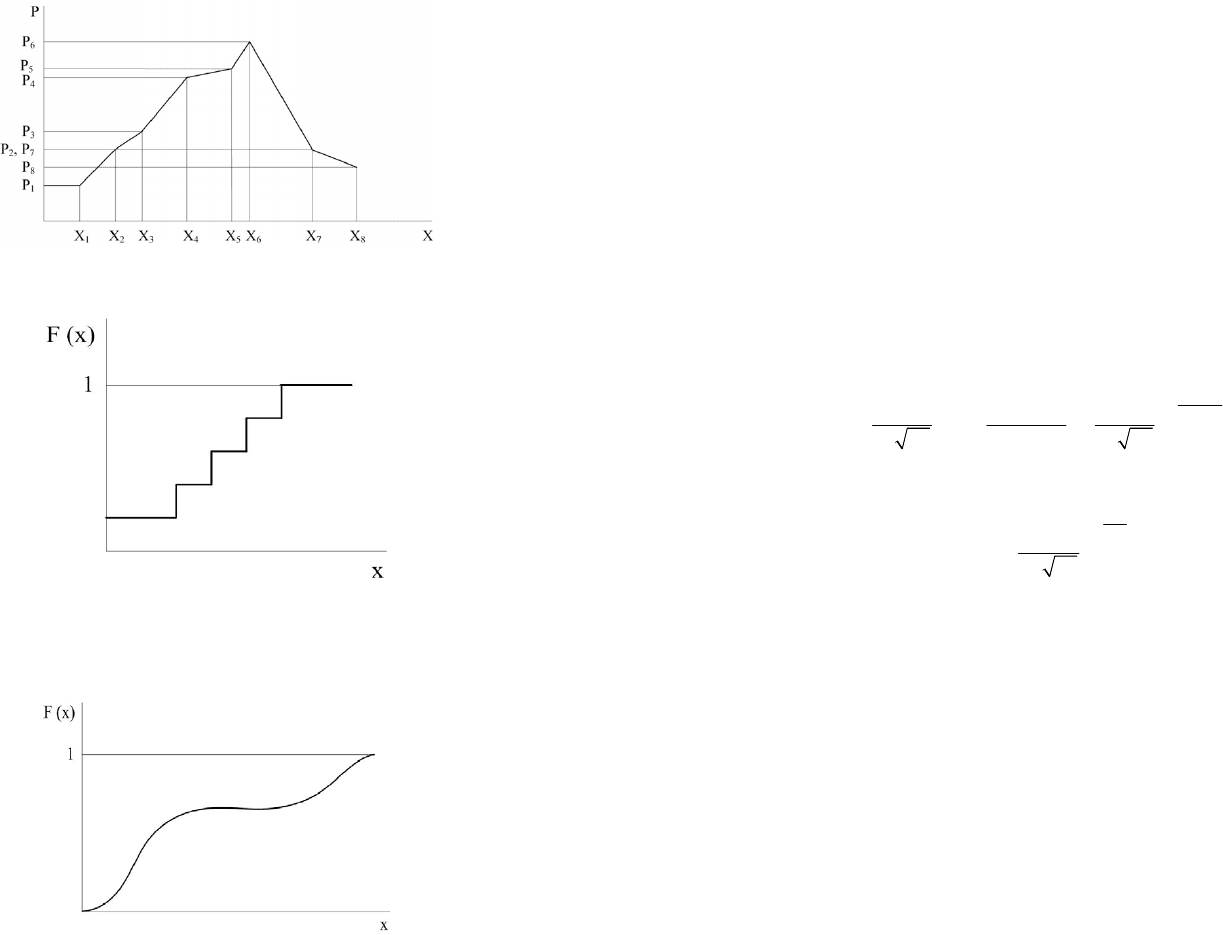
66
Рисунок 5.2 – Полигон распределения случайной величины
Рисунок 5.3 – Интегральная функция распределения
случайной дискретной величины
Рисунок 5.4 – Интегральная функция распределения непрерывной
случайной величины
83
5.6 Нормальный закон распределения
В различных отраслях науки и техники закон нормального распределения
нашел наибольшее применение. Ему подчиняются многие случайные непре-
рывные величины. Широкое применение закона нормального распределения
объясняется центральной предельной теоремой, из которой следует, что, если
случайная величина
X представляет собой сумму взаимно независимых случай-
ных величин
x
1
, x
2
, …x
n
, влияние каждой из которых на всю сумму незначи-
тельно, то независимо от того, каким законам распределения подчиняются каж-
дое из слагаемых
x
n
, сама величина X будет иметь распределение вероятностей,
близкое к нормальному и тем точнее, чем больше число слагаемых.
Дифференциальная функция распределения результатов наблюдений или
плотность вероятности распределения случайной непрерывной величины, под-
чиняющейся нормальному закону, имеет вид:
()
()
()
2
x
2
x
xm
2
2
x
x
2
x
xx
xm
11
px exp e
2
22
⎡
⎤
−
⎢
⎥
−
σ
⎢
⎥
⎣
⎦
⎡⎤
−
=−=
⎢⎥
σ
σπ σπ
⎢⎥
⎣⎦
, (5.38)
а для случайной погрешности:
2
0
2
2
0
1
pe
2
∆
⎡
⎤
⎢
⎥
∆
−
⎢
⎥
σ
⎢
⎥
⎣
⎦
∆
∆
⎛⎞
∆=
⎜⎟
σπ
⎝⎠
, (5.39)
где
х — переменная случайной величины (результат наблюдений);
x
,
∆
σσ —
среднеквадратичное отклонение результатов наблюдений случайной состав-
ляющей их погрешности; m
x
— математическое ожидание; е = 2,71828 — осно-
вание натуральных логарифмов.
Следует помнить, что
x
∆
σ=σ.
Дифференциальная функция нормального распределения имеет вид коло-
колообразной кривой (кривая Гаусса) (рис. 5.20). Кривая нормального распре-
деления случайной величины
х результатов измерений симметрична относи-
тельно математического ожидания.
Если
х — результаты многократных наблюдений одной и той же детер-
минированной физической величины, то данная кривая симметрична относи-
тельно математического ожидания результатов этих наблюдений. Если в каче-
стве случайной величины принята случайная погрешность
0
∆
со среднеквадра-
тичным отклонением ад, то эта кривая симметрична относительно оси ординат
(рис. 5.21).
82
Рисунок 5.17 – Кривая распределения
с положительной асимметрией (
k
0
ρ
> )
Рисунок 5.18 – Кривая распределения
с отрицательной асимметрией (
k
0
ρ
< )
При симметричном распределении
k
0
ρ
= .
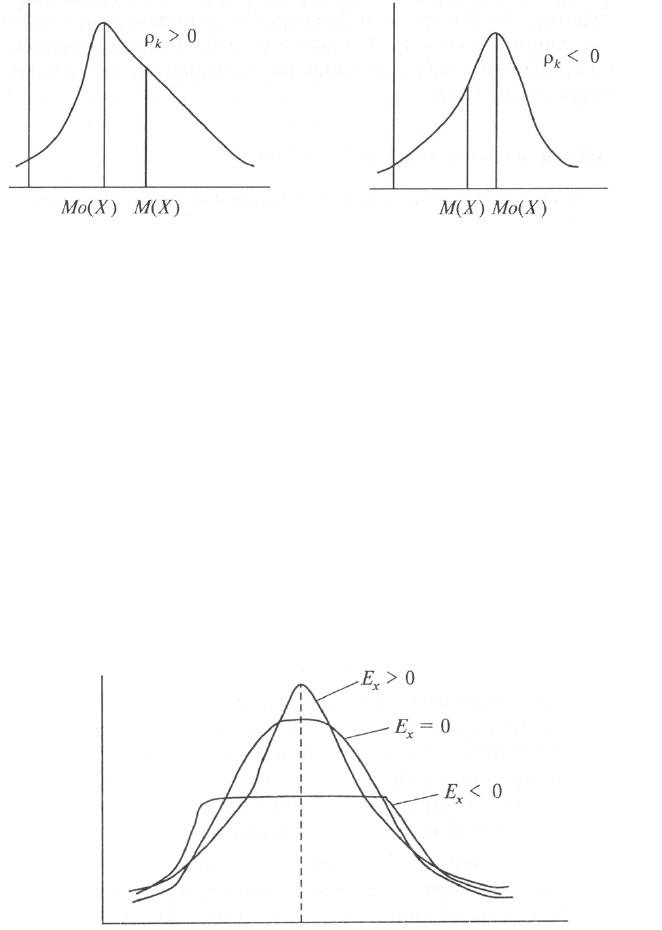
Как уже отмечалось, четвертый центральный момент
4
µ характеризует
свойство островершинности кривой распределения. На практике обычно ис-
пользуют не сам момент, а безразмерную величину, так называемый коэффици-
ент эксцесса (или просто эксцесс) коэффициент асимметрии:
(
)
4
x4x
E/3
=
µσ−. (5.37)
При симметричном одномодальном распределении эксцесс обычно поло-
жителен (
x
E0> ), если кривая распределения островершинная, и отрицателен,
если (
x
E0< ) кривая распределения плосковершинная (рис. 5.19). Если Ех = 0,
то кривая распределения соответствует нормальному закону.
Рисунок 5.19 – Кривые распределения с различной величиной
коэффициента эксцесса
67
5.4 Интегральная и дифференциальная функции распределения
случайных величин
Рассмотрим результат наблюдения X определенной или так называемой
детерминированной ФВ Q как случайную величину (СВ), принимающую зна-
чения Х
i
при различных наблюдениях.
Как уже отмечалось выше, в теории вероятностей событие, которое мо-
жет произойти или не произойти, называется случайным. Наиболее универ-
сальный способ описания СВ заключается в нахождении их интегральных или
дифференциальных функций распределения (ФР).
Интегральной функцией распределения результатов наблюдений является
зависимость от величины х вероятности Р того, что
результат наблюдений X
i
окажется меньше х:
(
)
{
}
{
}
Fx PX x P X x=≤=−∞<<. (5.5)
Другими словами интегральной функцией распределения случайной ве-
личины X называется вероятность выполнения неравенства X < х.
Интегральная функция F(x) обладает следующими свойствами:
1) F(x) — неубывающая функция;
2) F(x) при
x →+∞ стремится к 1;
3) F(x) при
x →−∞ стремится к 0;
4) F(x) — функция непрерывная, так как результат наблюдений в опреде-
ленном интервале может принять любое значение.
Однако четвертое свойство, как правило, не реализуется. Это обусловле-
но тем, что применяемые СИ имеют конечное разрешение: для стрелочного
прибора — цена деления шкалы (квант ФВ), для цифровых приборов — это це-
на наименьшего разряда кода
, поэтому реально функция распределения имеет
ступенчатый вид (рис. 5.5).
Несмотря на это, часто в метрологической практике интегральную
функцию распределения принимают непрерывной, что значительно упро-
щает анализ.
Для случайной погрешности, как и для случайной величины, имеется своя
интегральная функция распределения:
{
}
(
)
(
)
{
}
{
}
ii i
FP PXQ xQ PXx
∆
=∆≤∆= − ≤− = ≤
. (5.6)
Интегральная функция F(x), как и вероятность, является безразмерной ве-
личиной.
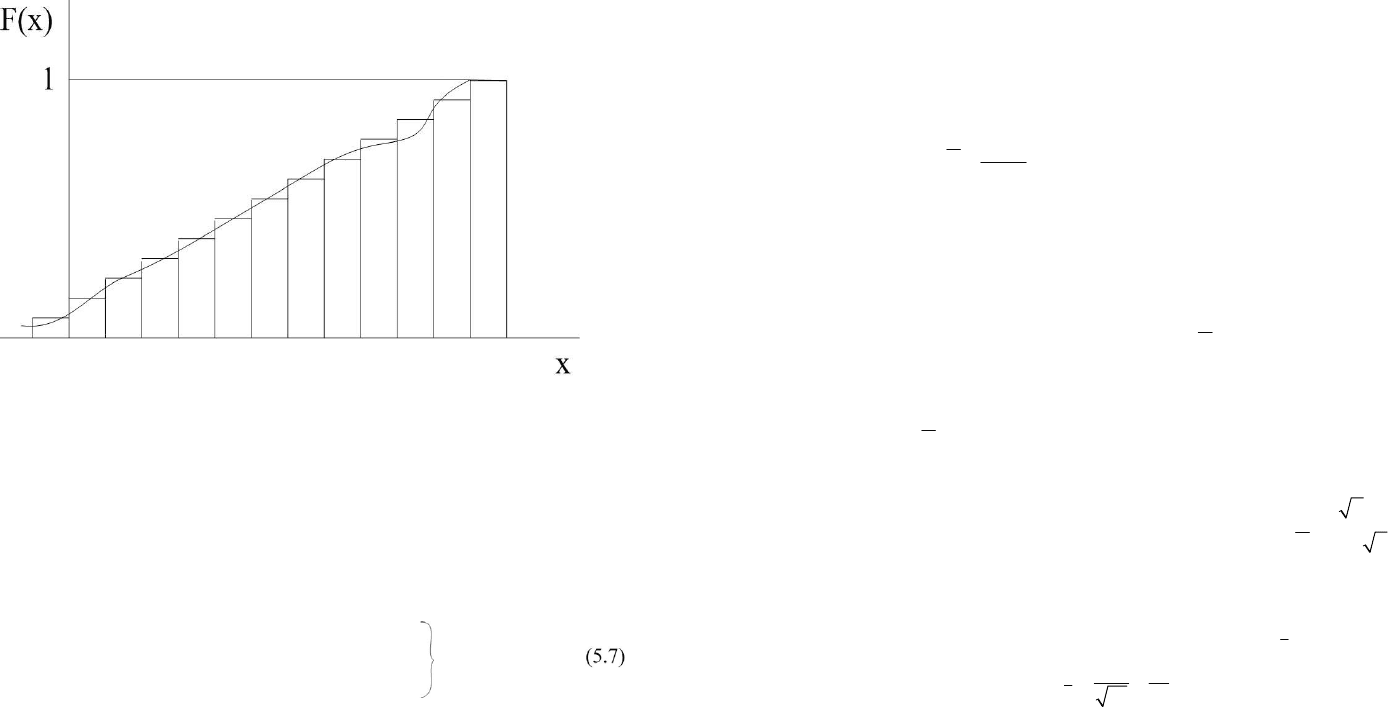
68
Рисунок 5.5 – Реальная функция распределения
Более удобно и наглядно описывать свойство результатов наблюдений с
помощью дифференциальной функции распределения, которая называется
плотностью распределения. Отметим, что дифференциальные функции резуль-
татов наблюдений X и случайной погрешности
0
∆
совпадают, только начало
координат для
0
∆ располагается в нулевой точке.
Для результатов наблюдений:
(
)
(
)
;/ dxxdFxp
xx
=
для погрешности:
000
/ ∆∆∆
∆∆
ddFp
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
.
График дифференциальной функции распределения или кривая распреде-
ления чаще всего представляет собой симметричную функцию с максимумом в
точке Q для результатов наблюдений (рис. 5.6). Кривая распределения для слу-
чайной погрешности также чаще всего представляет собой симметричную
функцию, но с максимумом в точке 0 (рис. 5.7).
Для результатов наблюдений
:
(
)
(
)
;/ dxxdFxp
xx
=
(5.8)
для случайной погрешности:
000
/ ∆∆∆
∆∆
ddFp
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
. (5.9)
81
стики (математическое ожидание, дисперсию и др.). С точки зрения теории из-
мерений, наибольший интерес представляет изучение числовых характеристик
среднего арифметического значения этих величин.
Обозначив среднее арифметическое значение рассматриваемых случай-
ных величин как
in
i
i1
X
X
n
=
=
=
∑
, установим связь между числовыми характеристи-
ками этого среднего арифметического значения и соответствующими характе-
ристиками математического ожидания, дисперсии, среднеквадратичного откло-
нения и среднего арифметического значения случайной величины.
1. Математическое ожидание среднего арифметического значения одина-
ково распределенных взаимно не связанных случайных величин равно матема-
тическому ожиданию
а каждой из величин:
(
)
MX a
=
.
2. Дисперсия среднего арифметического значения n
одинаково распреде-
ленных независимых случайных величин в n
раз меньше дисперсии D каждой
из величин:
()
DX D/n= .
3. Среднеквадратичное отклонение среднего арифметического значения n
одинаково распределенных независимых случайных величин в
n раз меньше
среднеквадратичного отклонения
σ
каждой из величин:
(
)
X/nσ=σ .
Пример.
Среднеквадратичное отклонение каждой из 16 одинаково рас-
пределенных взаимно независимых случайных величин равно 10. Найти сред-
неквадратичное отклонение среднего арифметического
X
σ
этих величин.
X
10
2,5
4
16
σ
σ= = =
Асимметрия и эксцесс. Как уже говорилось выше, в теории измерений
используют третий
3
µ
и четвертый
4
µ
центральные моменты. Третий цен-
тральный момент характеризует степень асимметрии кривой распределения от-
носительно математического ожидания. На практике обычно используют не
сам момент, а безразмерный коэффициент асимметрии
3
k3x
/
ρ
=µ σ .
При одномодальном распределении, если
k
0
ρ
>
, асимметрия положи-
тельна, т. е. мода Мо(Х) находится слева от математического ожидания М(Х)
(рис. 5.17), и отрицательна (
k
0ρ< ), т. е. мода Мо(Х) находится справа от мате-
матического ожидания М(Х) (рис. 5.18).
80
Рисунок 5.16 – Плотность вероятности результатов
Чем больше а, тем более пологой и расплывчатой становится функция
распределения.
Дисперсия обладает четырьмя свойствами.
Свойство 1. Дисперсия постоянной величины равно нулю: Д(С) = 0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии,
возведя его в квадрат:
(
)
(
)
2
DCX CDX= . (5.33)
Свойство 3. Дисперсия суммы двух независимых случайных величин
равна сумме дисперсий этих величин.
(
)
(
)
(
)
DX Y DX DY+= + . (5.34)
Свойство 4. Дисперсия разности двух независимых случайных величин
равна сумме дисперсий этих величин:
(
)
(
)
(
)
DX Y DX DY−= + . (5.35)
На основании этого свойства среднеквадратичное отклонение суммы ко-
нечного числа взаимно независимых случайных величин равно квадратному
корню из суммы квадратов среднеквадратичных отклонений этих величин:
()()()()
22 2
12 n 1 2 n
X X ... X X X ... Xσ+++ =σ +σ ++σ
. (5.36)
Известно, что по закону распределения можно найти числовые характе-
ристики случайной величины. Это означает, что если несколько случайных ве-
личин имеют одинаковые законы распределения, то их числовые характеристи-
ки одинаковы.
Рассмотрим n
независимых случайных величин Х
1
, Х
2
,…, Х
n
, которые
имеют одинаковые распределения, а следовательно, и одинаковые характери-
69
Рисунок 5.6 – Дифференциальные
функции распределения
Рисунок 5.7 – Кривая распределения
для случайной погрешности
Таким образом, дифференциальная функция распределения результатов
наблюдений или случайной погрешности получается дифференцированием ин-
тегральной функции распределения.
Существуют и несимметричные функции распределения, например, функция
Релея (рис. 5.8) или функции, не имеющие максимума (равномерная или трапе-
циевидная) (рис. 5.9 и 5.10).
Интегральная функция связана с
дифференциальной следующим образом:
() ()
x
xx
Fx p xdx
−∞
=
∫
, поскольку
(
)
x
F1
+
∞=, то
()
x
x
pxdx1
−∞
=
∫
.
То есть площадь под кривой функции распределения равна 1, что и является
ус-
ловием нормировки.
Рисунок 5.8 – График функции Релея
70
Рисунок 5.9 – График функции, не
имеющей максимума (равномерная)
Рисунок 10 – График функции, не
имеющей максимума (трапециевидная)
Размерность плотности распределения вероятностей обратная размерно-
сти измеряемой физической величины, так как интегральная функция распре-
деления является безразмерной. Используя понятие функции распределения,
можно получить выражение для вероятности того, что результат наблюдений
находится в полуоткрытых интервалах [
х
1
, х
2
] или [
00
2
1
,
∆
∆ ]:
{
}
}
{
}
{
(
)
(
)
12 2 1x2x1
Px Xx P Xx P Xx Fx Fx<≤ = −∞<≤ −−∞<≤ = −
; (5.10)
{
}
}
}
000 00 00 0 0
1 21
221xx
PP P FF
⎧⎧
⎛⎞ ⎛⎞
∆ < ∆ ≤ ∆ = −∞ < ∆ ≤ ∆ − −∞ < ∆ ≤ ∆ = ∆ − ∆
⎨⎨
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⎩⎩
. (5.11)
Это выражение указывает на то, что вероятность попадания результата
наблюдения X или случайной погрешности измерения
0
∆
в заданный интервал
равна разности значений интегральной функции распределения на указанных
границах этого интервала.
Выразив эту вероятность через дифференциальную функцию распределе-
ния или плотность распределения вероятности, получим:
{ } ( ) ( ) () () ()
212
1
xxx
12x2x2x x x
x
Px X x Fx Fx Pxdx Pxdx Pxdx
−∞ −∞
<≤ = − = − =
∫∫∫
; (5.12)
{
}
21 2
1
000 0 0 00 00 00
121
2
PFFPdPdPd
∆∆ ∆
∆∆ ∆ ∆ ∆
−∞ −∞ ∆
⎛ ⎞ ⎛ ⎞ ⎛⎞ ⎛⎞ ⎛⎞
∆<∆≤∆= ∆− ∆= ∆∆− ∆∆= ∆∆
⎜ ⎟ ⎜ ⎟ ⎜⎟ ⎜⎟ ⎜⎟
⎝ ⎠ ⎝ ⎠ ⎝⎠ ⎝⎠ ⎝⎠
∫∫∫
. (5.13)
Вероятность попадания результата наблюдений X или случайной по-
грешности
0
∆
в заданный интервал численно равна площади под кривой плот-
ности распределения вероятности, ограниченной границами интервала
(рис. 5.11).
79
р ..................... 0,3 0,5 0,2.
Найдем математическое ожидание величины X:
(
)
M X 1 0,3 2 0,5 5 0,2 2,3=⋅ + ⋅ +⋅ = .
Определим все возможные значения квадратов отклонений:
() ( )
2
2
1
xMX 12,3 1,69−=−=
⎡⎤
⎣⎦
;
() ( )
2
2
2
xMX 22,3 0,09−=−=⎡⎤
⎣⎦
;
() ( )
2
2
3
xMX 52,3 7,29−=−=
⎡⎤
⎣⎦
.
Закон распределения величин
()
2
1
xMX−
⎡
⎤
⎣
⎦
,
()
2
2
xMX−
⎡
⎤
⎣
⎦
,
()
2
3
xMX−⎡⎤
⎣⎦
тот же, что и X.
Отсюда:
() ()
2
D X M X M X 1,69 0,3 0,09 0,5 7,29 0,2
0,507 0,045 1,458 2,01 .
=− =⋅+⋅+⋅=⎡⎤
⎣⎦
=++=
Очевидно, что дисперсия равна разности между математическим ожида-
нием квадрата случайной величины и квадратом ее математического ожидания:
() () () ()
() () () ()
2
22
2
2
DX MX MX MX 2XMX M X
MX 2MXMX M X .
⎡
⎤
=− = − + =
⎡⎤
⎣⎦
⎣
⎦
=− +
Поскольку математическое ожидание М(Х) является величиной постоян-
ной, то 2М(Х) и М
2
(Х) также постоянные величины, следовательно: D(X) =
М(Х
2
) − [М(Х)]
2
.
Найдем дисперсию случайной величины предыдущего примера:
(
)
2
M X 1 0,3 4 0,5 25 0,2 0,3 2,0 5,0 7,3=⋅ + ⋅ + ⋅ = + + = ;
(
)
22
(M X ) (1 0,3 2 0,5 5 0,2) 5,29=⋅ +⋅ +⋅ = ;
() ()
2
DX MX MX 7,3 5,29 2,01=− =−=
⎡⎤
⎣⎦
.
Дисперсия случайной погрешности является характеристикой рассеяния
результатов наблюдений относительно математического ожидания.
Дисперсия имеет размерность квадрата измеряемой физической величи-
ны, поэтому значительно чаще в метрологической практике пользуются
средне-
квадратичным отклонением
(СКО) результатов наблюдений:
(
)
DXσ= . СКО
имеет размерность измеряемой физической величины.
Плотность вероятности результатов наблюдений при различных значени-
ях СКО погрешности представлена на рисунке 5.15.
