Новосельцева Т.А., Корепанова В.С. Метрология
Подождите немного. Документ загружается.

78
В теории измерений важное значение имеет 2-й центральный момент, на-
зываемый дисперсией результатов наблюдений или дисперсией случайной по-
грешности
[]
DX.
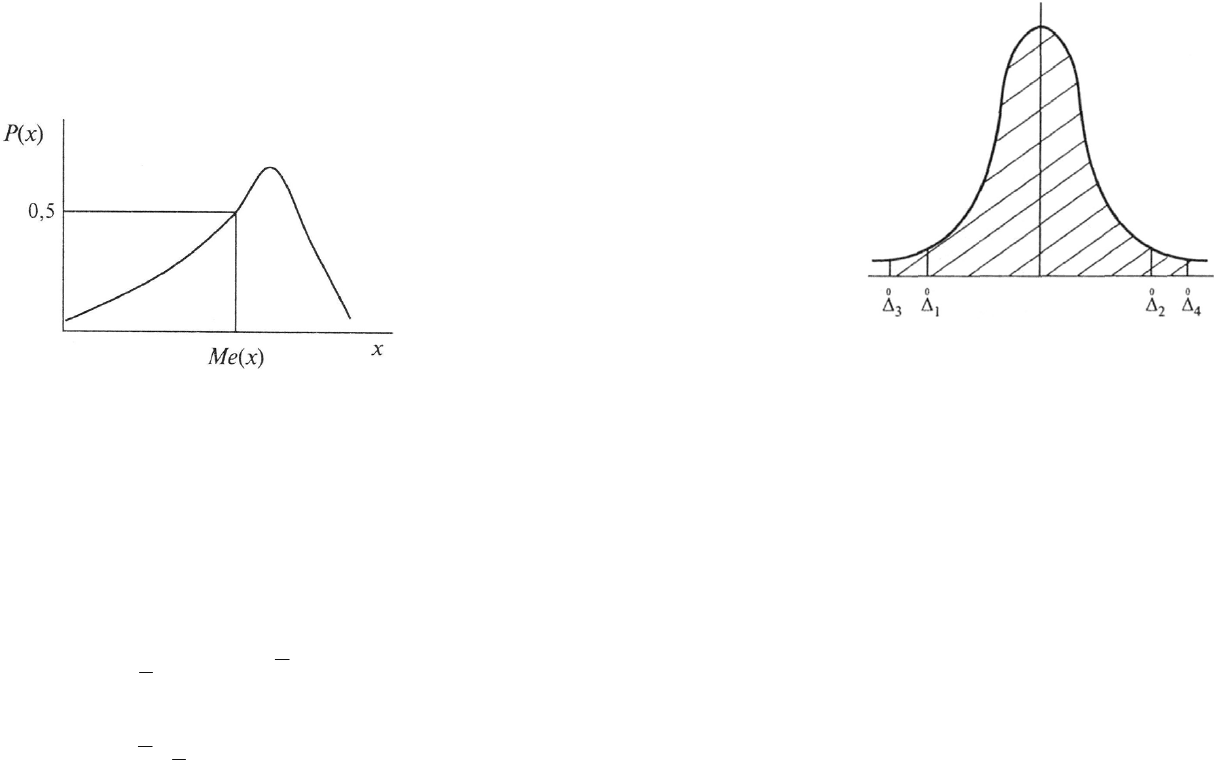
Рисунок 5.15 – Определение медианы случайной величины
Для случайной
непрерывной величины:
[]
() ()()
2
00
22
xxx
2
000
DX D M X m M X m p xdx
pd.
∞
−∞
∞
∆
−∞
⎡⎤
⎡⎤
⎡⎤
=∆= − = ∆= − =
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣⎦
⎛⎞
=∆ ∆ ∆
⎜⎟
⎝⎠
∫
∫
(5.30)
Для случайной
дискретной величины:
[]
()
()
in
2
2ii
i1
1
DX Px x X
n
=
=
=µ = −
∑
, (5.31)
где
in
i
i1
1
Xx
n
=
=
=
∑
. (5.32)
Дисперсией случайной дискретной величины является математическое
ожидание разницы квадрата отклонений каждого значения этой величины от ее
математического ожидания: D(X) = М[Х - М(Х)]
2
. Исходя из этого определения,
для того, чтобы найти дисперсию, надо вычислить сумму произведений воз-
можных значений квадрата отклонения на их вероятности.
Пример. Найти дисперсию случайной величины X, которая задана сле-
дующим законом распределения:
х ..................... 1 2
5;
71
Рисунок 5.11 – Определение вероятности попадания результата
наблюдений X или случайной погрешности
0
∆
в заданный интервал
Произведение
(
)
x
pxdx называется элементом вероятности. В том слу-
чае, если закон распределения плотности вероятности близок к так называемо-
му нормальному закону, как видно из графика дифференциальной функции рас-
пределения, то наиболее вероятны малые значения погрешностей. Вероятность
появления больших погрешностей значительно меньше. Результаты наблюде-
ний сконцентрированы вокруг истинного значения измеряемой ФВ, и по мере
приближения к
нему элементы вероятности возрастают. Это дает основание
принять за оценку истинного значения ФВ абсциссу центра тяжести фигуры,
образованной осью абсцисс и кривой плотности распределения. Эта характери-
стика случайной величины называется математическим ожиданием:
[]
()
xx
MX m xp xdx
∞
−∞
==
∫
. (5.14)
Дадим математически строгое определение случайной и систематической
погрешностям.
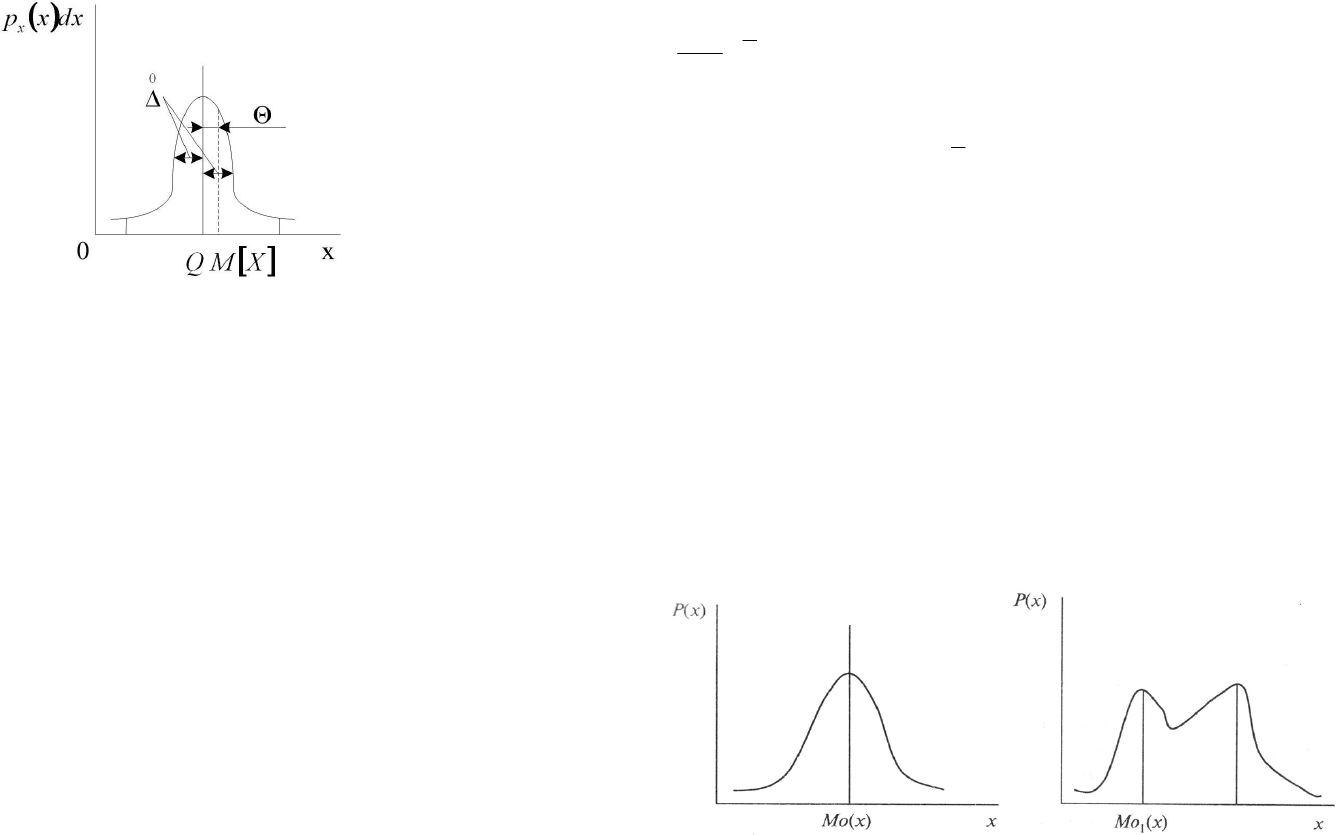
Систематическая погрешность Θ (рис. 5.12) математического ожида-
ния результатов наблюдения от истинного значения измеряемой физической
величины:
[
]
MX Q
Θ
=−. (5.15)
72
Рисунок 5.12 – Определение систематической погрешности
Случайная погрешность
0
∆
— разность между результатом единичного
наблюдения и математическим ожиданием результатов наблюдений:
[]
0
XMX∆= − , (5.16)
отсюда действительное значение измеряемой физической величины равно:
0
д
XX
=
−Θ−∆. (5.17)
5.5 Характеристики случайных величин
Распределение случайной величины характеризуется некоторыми чис-
ленными параметрами —
моментами, являющимися мерами положения, рас-
сеяния, остро- (или плоско-) вершинности и асимметрии.
К характеристикам мер положения относятся: математическое ожидание,
среднее арифметическое значение, мода, медиана. К характеристикам мер рас-
сеяния относятся дисперсия и среднеквадратическое отклонение (СКО). Остро-
(или плоско-) вершинность может характеризоваться эксцессом, а параметры
асимметрии — коэффициентом асимметрии.
Моменты функции распределения могут
быть следующими.
Моментом ряда распределения М
к
(или просто моментом) случайной дис-
кретной
величины относительно начального значения x=a а называется сумма
произведений отклонений значений
i
x , относительно a в степени к на соответ-
ствующую частоту Р
x
:
77
()() ()
()
kn
k
k1
11 2 2 k k 1 1 2 2 k k
11 2 k k k 11 22 kk
x
X xm x m ... x m /n x m /n x m /n ... x m /n
n
x w x w ... x w x p x p ... x p M X
=
=
== + ++ = + ++ =
=+ ++ ≈+++=
∑
то есть:
(
)
XMX= . (5.29)
Это имеет большое практическое значение, так как на практике при обра-
ботке результатов измерений для оценки истинного значения измеряемой фи-
зической величины наиболее часто используют именно среднее арифметиче-
ское значение ряда наблюдений, а не математическое ожидание или какой-либо
другой параметр.
Математическое ожидание, как и мода Mo(x), и медиана Me(x)
относятся
к характеристикам положения функции распределен и я случайной величины.
Модой называют значение случайной величины, имеющей для дискрет-
ной величины наибольшую вероятность, а для непрерывной — наибольшую
плотность вероятности. Если кривая распределения имеет один максимум, то
мода равна значению случайной величины, соответствующей этому максиму-
му. Такая кривая называется одномодальной (рис. 5.13). Если кривая распреде-
ления имеет два или несколько максимумов, то он а , соответственно называет-
ся двухмодальной или многомодальной (рис. 5.14).
Рисунок 5.13 – Одномодальная
кривая распределения
Рисунок 5.14 – Двухмодальная
(многомодальная) кривая распределения
Медианой случайной величины X называют такое её значение, для кото-
рого функция распределения равна 0,5 (рис. 5.15)
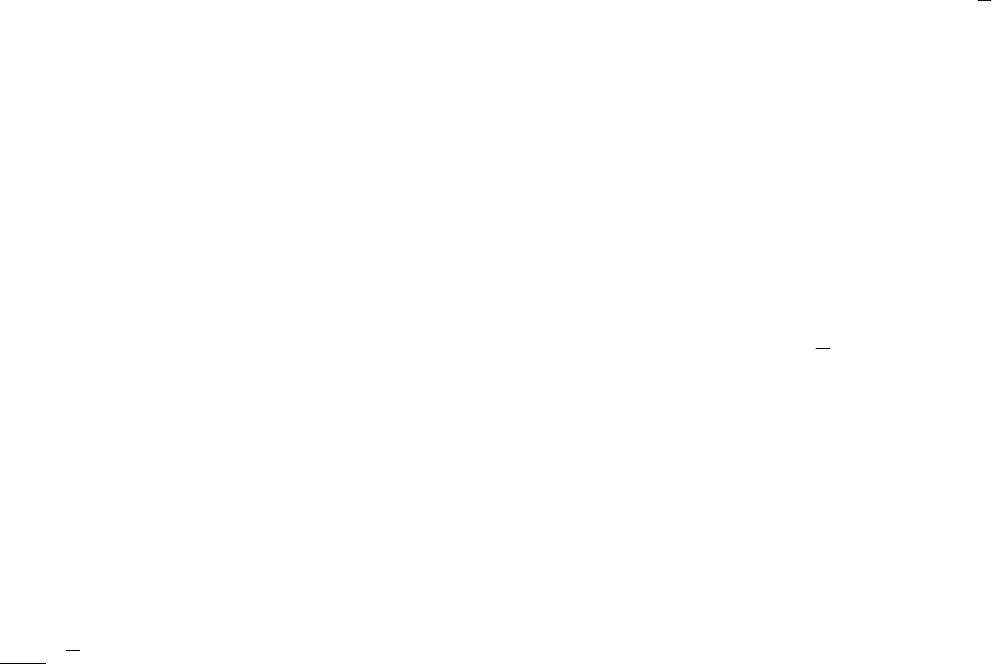
76
Составив все возможные значения величины х + у, получим:
(х
1
+ у
1
), (х
1
+ у
2
), (х
2
+ у
1
), (х
2
+ у
2
).
Событие, состоящее в том, что X примет значение х
i
, (вероятность этого
события равна p
1
), влечет за собой событие, которое состоит в том, что Х +Y
примет значение х
1
+ y
1
или х
1
+ у
2
(вероятность этого события по теореме
сложения равна (p
1
q
1
+ p
1
q
2
= p
1
) и обратно. Аналогично доказывается, что
p
2
q
1
+p
2
q
2
= р
2
и т. д.
Таким образом, М ( Х +Y)=М ( Х ) + M(Y).
Следствием этого является то, что математическое ожидание суммы не-
скольких независимых случайных величин равно сумме их математических
ожиданий:
М(Х+Y+Z)=М ( Х ) + M(Y)+M(Z). (5.27)
Вероятностный смысл математического ожидания заключается в том, что
при достаточно большом числе независимых испытаний (чем больше, тем точ-
нее) оно приближенно равно среднему арифметическому значению этого ряда
чисел.
Пусть проведено n испытаний, в которых величина X приняла m
1
раз зна-
чение x
1
, m
2
– x
2
, x
k
– m
k
, причем
12 k
mm...m n
+
++ =.
Сумма всех значений, которые приняла величина X в n независимых ис-
пытаний, определяется следующим образом:
kn
k1122 kk
k1
x x m x m ... x m
=
=
=+ ++
∑
.
Разделив левую и правую часть этого равенства на n, получим:
kn
k
k1
11 2 2 k k
x
Xxm xm ...xm/n
n
=
=
== + ++
∑
, (5.28)
где отношения (m
1
/n), (m
2
/n),…, (m
k
/n) представляют собой относительную час-
тоту
k
w (частость) выпадения соответствующих значений х
k
.
В соответствии с теоремой Бернулли:
Если в каждом из
n независимых испытаний вероятность р появления со-
бытия
А постоянна, то как угодно близка к единице вероятность того, что от-
клонение относительной частоты w от вероятности
р по абсолютной величине
будет сколь угодно малым, если число испытаний достаточно велико, то при-
нимаем
k
wp≈ .
Таким образом:
73
()
in
k
kxi
i1
1
MPXa
n
=
=
=−
∑
. (5.18)
Моментом ряда распределения М
k
(или просто моментом) случайной
непрерывной
величины относительно начального значения х=а называется
интеграл от минус бесконечности (
−
∞ ) до плюс бесконечности (+∞ ) произ-
ведений отклонений значений X
i
относительно а в степени к на соответст-
вующую частоту Р
x
:
()
k
kxi
MPXadx
∞
−∞
=−
∫
. (5.19)
Давая показателю
к значения 0, 1, 2, 3 и т. д., получим моменты нулевого,
первого, второго и т. д. порядков относительно начала
а.
Различают начальные и центральные моменты
к-го порядка:
если а = 0, то это
начальный момент;
если а =
X, то это центральный момент.
В литературе часто начальные моменты обозначают буквой
ν с соответ-
ствующими индексами, а центральные моменты
µ
— также с индексами.
В теории измерений и метрологической практике обычно используют
первый начальный
1
ν
, второй
2
ν
, третий
3
µ
и четвертый
4
µ
центральные мо-
менты.
Начальный момент порядка
к случайной величины X называется мате-
матическим ожиданием
величины Х
k
:
(
)
k
k
MXν=
;
(
)
1
MXν= ;
(
)
2
2
MXν=
;
(
)
3
3
MXν=
;
(
)
4
4
MXν=
.
Центральные моменты можно выразить через начальные следующим
образом:
0
1µ=
;
1
0µ= ;
2
221
µ=ν−ν;
3
33 21 1
32µ=ν−νν+ν;
24
44 31 21 1
463µ=ν−νν+νν−ν.
Центральный момент порядка к случайной величины X называется ма-
тематическим ожиданием величины [X
−
М(Х)
k
]:
()
(
)
k
k
MXMX
⎡⎤
µ= −
⎣⎦
;
()
(
)
1
1
MXMX 0
⎡⎤
µ= − =
⎣⎦
;
()
(
)
2
2
MXMX
⎡
⎤
µ= −
⎣
⎦
. (5.20)
74
Второй центральный момент
()
(
)
2
2
MXMX
⎡
⎤
µ= −
⎣
⎦
называется
дисперси-
ей
и обозначается D(X).
Таким образом,
дисперсия — это математическое ожидание величины [Х
−
М(Х)
2
].
Моменты более высоких порядков в метрологии, как правило, не исполь-
зуются.
Первый начальный момент —
математическое ожидание представляет
собой оценку истинного значения случайной величины. При измерениях, как
правило, имеют дело со случайными дискретными величинами.
Математическое ожидание дискретной случайной величины представляет
собой сумму произведений всех ее возможных значений на вероятности их по-
явления.
Предположим, что случайная величина может принимать только значения
x
1
, x
2
, …x
n
, вероятности появления которых соответственно равны p
1
, p
2
, …p
n
.
Тогда математическое ожидание дискретной случайной величины X опреде-
лится как:
()
in
ii
i1
MX xp
=
=
=
∑
. (5.21)
Следует отметить, что математическое ожидание случайной величины
есть величина не случайная, а постоянная и вполне определенная.
Пример. Найти математическое ожидание случайной величины X, зная
закон ее распределения:
х ..................... 3 5 2;
р ..................... 0,1 0,6 0,3.
Искомое математическое ожидание:
(
)
M X 3 0,1 5 0,6 2 0,3 3,9=⋅ +⋅ +⋅ = .
Математическое ожидание обладает следующими свойствами.
Свойство 1. Математическое ожидание постоянной величины С равно
самой величине, т. е. М(Х) = С.
Доказательство. Будем рассматривать постоянную С как дискретную
случайную величину, которая имеет только одно возможное значение С и при-
нимает его с вероятностью р = 1.
Тогда:
(
)
M СС1 С
=
⋅= . (5.22)
Свойство 2. Постоянный множитель можно выносить за знак математи-
ческого ожидания:
75
(
)
(
)
M СXCMX
=
. (5.23)
Доказательство. Предположим, что случайная величина х заданa сле-
дующим законом распределения вероятностей
х ..................... x
1
x
2
… x
n
;
р ..................... p
1
p
2
… p
n
.
Будем рассматривать каждую величину x1, x2, …xn как произведение
i
1x⋅ , тогда математическое ожидание:
()
(
)
(
)
11 2 2 nn 11 22 nn
M CX Cx p Cx p ... Cx p C x p x p ... x p CM X=⋅+⋅++ = ⋅+ ++ = .
Свойство 3. Математическое ожидание произведения двух независимых
случайных величин равно произведению их математических ожиданий:
()
(
)
(
)
MXY MX MY
=
⋅ .
Доказательство. Зададим независимые случайные величины своими за-
конами распределения вероятностей:
х ..................... x
1
x
2
Y y
1
y
2
;
р ..................... p
1
p
2
q q
1
q
2
.
Выразим все значения, которые может принимать случайная величина
XY, перемножив все возможные значения X на каждое значение Y: (х
1
, у
1
), (х
2
,
у
1
), (х
1
, у
2
), (х
2
, у
2
). Учитывая, что если вероятность появления х
1
равна p
1
, а ве-
роятность появления у
1
равна q
1
, то вероятность появления (х
1
у
1
) равна (p
1
q
1
) и
т. д., получим:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
()()()()()()
()
11 11 21 21 1 2 12 2 2 2 2
11 11 2 2 2 2 11 2 2 11 2 2 11 2 2
MXY xypq xypq xypq xy pq
yq xp x p yq xp xp xp xp yq yq M X M Y .
=⋅+⋅+⋅+ ⋅=
=⋅ + + + = + ⋅ + = ⋅
то есть:
(
)
(
)
(
)
MXY MX MY
=
⋅ . (5.24)
Следствием этого является то, что математическое ожидание произведе-
ния нескольких независимых случайных величин равно произведению их мате-
матических ожиданий:
()
(
)
(
)
(
)
ZMYMXMXYZM
⋅
⋅
=
. (5.25)
Свойство 4. Математическое ожидание суммы двух независимых слу-
чайных величин равно сумме их математических ожиданий:
(
)
(
)
(
)
MX Y MX MY+= + . (5.26)
Доказательство. Предположим, что случайные величины х и Y заданы
своими законами распределения вероятностей:
х ..................... x
1
x
2
Y y
1
y
2
;
р ..................... p
1
p
2
q q
1
q
2
.

116
7. Рассчитывается оценка среднеквадратичного отклонения среднего
арифметического значения
x
σ :
а) если среднеквадратичное отклонение результата однократного измере-
ния известно заранее, то верхняя и нижняя границы доверительного интервала
∆±
среднего арифметического значения результатов измерений
i
xX− опре-
деляют по выражению:
ip
xX t
−
≤∆= σ; (7.20)
б) если среднеквадратичное отклонение результата однократного измере-
ния заранее неизвестно, то верхняя и нижняя границы доверительного интерва-
ла
±∆ среднего арифметического значения результатов измерений
i
xX− оп-
ределяют по выражению:
ipx
xX (t )/n−≤∆=σ , (7.20)
где
p
t — коэффициент Стьюдента.
8. Определяются границы не исключённой систематической погрешности
Θ
:
а) если отношение
x
/0,8Θσ< , то систематической погрешностью
Θ
пренебрегают и суммарная погрешность
Σ
∆
определяется случайной погреш-
ностью
px
(t ) / nσ , т. е.
px
(t ) / n
Σ
∆= σ ;
б) если отношение
x
/0,8Θσ> , пренебрегают случайной погрешностью и
суммарная погрешность определяется не исключёнными систематическим по-
грешностями
НСПΣ
∆=Θ ;
в) если выполняется условие
x
0,8 / 8
<
Θσ<, то суммарная погреш-
ность должна учитывать случайную и не исключённую систематическую
погрешности;
jm
22
j
x
j1
1
3
=
Σ
=
∆
=Θ+σ
∑
. (7.21)
9. Результаты представляются в следующем виде:
X , P ...
±
∆=
Часто измерения проводятся в несколько этапов, разными наблюдателями
и в различное время, в разных условиях с применением различных СИ. Каждо-
му этапу соответствует своя группа измерений со своими средними арифмети-
ческими значениями в каждой группе
X:
89
Рисунок 5.25 — Интегральная функция равномерного распределения
5.8 Наиболее часто применяемые законы распределения
случайных погрешностей
Дифференциальные функции распределения случайных погрешностей
могут подчиняться различным законам. Подавляющее число этих функций дос-
таточно хорошо описываются четырьмя законами распределения. В связи с
этим в метрологии для описания случайных погрешностей, как правило, ис-
пользуют ограниченный набор стандартных аппроксимирующих функций рас-
пределения: нормальную, равномерную, по треугольнику, по трапеции.
Нормальную функцию распределения имеют следующие случайные вели-
чины:
— погрешности, складывающиеся из достаточно большого числа (можно
считать, что более пяти независимых составляющих) при отсутствии домини-
рующей составляющей;
— флуктуационные (колебательные) погрешности разного рода;
— случайные погрешности средств измерений.
Равномерные функции распределения имеют:
— погрешности результатов наблюдений, округленных в ближайшую
сторону отсчетов с неточностью целого (или долевого) деления шкалы;
— погрешность приближенных вычислений с округлением до ближайшей
значащей цифры;
— погрешности регулировки в допустимых пределах ±
а;
— погрешности, связанные с зазорами;
— погрешности, связанные с изменением температуры в допустимых
пределах;
— вариация показаний измерительных приборов.
90
Треугольные функции распределения (по Симпсону) имеют погрешности
измерений длины, угла, интервала времени по двум отсчетам (начало — конец).
По этому закону распределены, например, погрешности суммы или разности
двух равномерно распределенных величин. Например, если отклонения разме-
ров отверстия и вала распределены в пределах их допусков равномерно, а до-
пуски вала и отверстия примерно одинаковы, то
зазоры в пределах их допуска
будут распределены по закону треугольника.
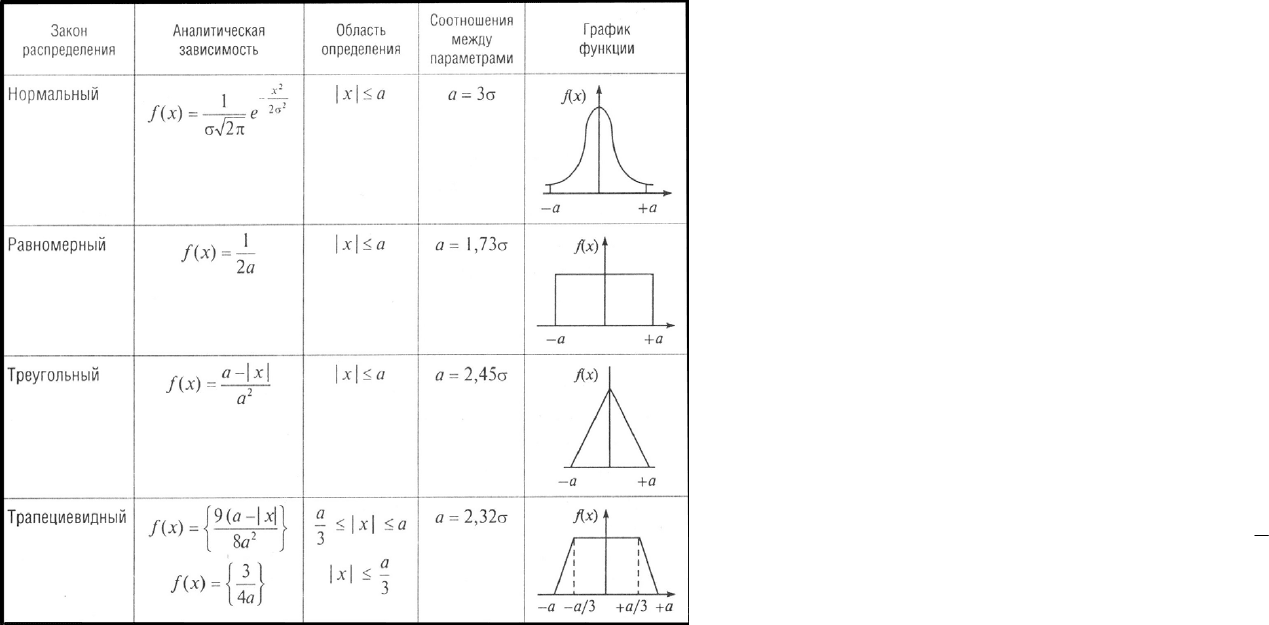
Аналитические зависимости, области определения, соотношения между
параметрами и графики наиболее часто используемых законов распределения
представлены в таблице 5.1.
Таблица 5.1 — Наиболее часто применяемые законы распределения
115
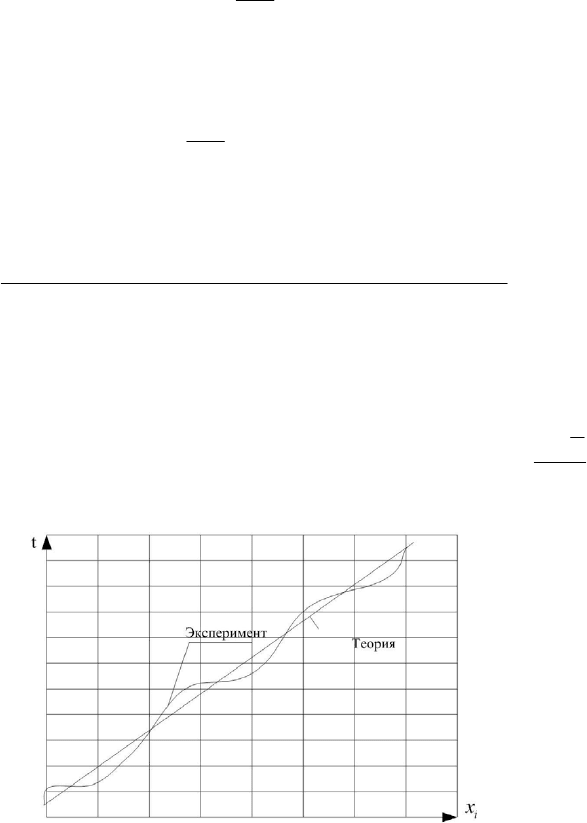
Если экспериментальная зависимость существенно отклоняется от пря-
мой линии, гипотеза о нормальном законе распределения результатов наблюде-
ний отвергается.
Таким образом, оценка истинного значения измеряемой физической ве-
личины сводится к определению этого значения X как функции результата из-
мерения и полученной суммарной погрешности:
(
)
ii
xfX ∆
+
=
. Другими сло-
вами, необходимо получить оценку истинного значения измеряемой физиче-
ской величины и границы доверительного интервала, внутри которого она на-
ходится, с принятой доверительной вероятностью.
Для обработки результатов прямых измерений с многократными наблю-
дениями используется следующий алгоритм
.
Если отсутствует надежная предварительная информация о том, что ре-
зультаты многократных измерений являются равно-рассеянными, проводится
проверка этой гипотезы (о равнорассеянности результатов измерений) любым
способом (например, с помощью критериев Фишера или Романовского)
.
Если полученный ряд результатов многократных наблюдений можно счи-
тать равнорассеянным, дальнейшая обработка результатов выполняется в сле-
дующем порядке
.
1. Если есть подозрения на наличие в исправленном ряде результатов на-
блюдений грубых погрешностей, он проверяется на их наличие любыми из-
вестными способами (например, с помощью критериев Смирнова, Шовенье и
др.). Обнаруженные грубые погрешности исключаются из дальнейшего рас-
смотрения
.
2. Ряд равнорассеянных результатов многократных наблюдений проверя-
ется на наличие систематических погрешностей любым методом (например, с
помощью критериев Аббе, Бартлета и др.).
3. Обнаруженные систематические погрешности исключаются из резуль-
татов наблюдений путем введения соответствующих поправок.
4. Полученный ряд результатов наблюдений выстраивается в вариацион-
ный ряд, и проводится проверка гипотезы о том, что
этот ряд соответствует за-
кону нормального распределения.
5. В случае нормального закона распределения результатов наблюдений
вычисляется среднее арифметическое значение
X этих наблюдений, поскольку
в этом случае оно является наиболее оптимальной оценкой истинного значения
измеряемой физической величины.
6. Вычисляется среднеквадратичное отклонение результата измерений
σ
.
114
В том же диапазоне чисел измерений (15 < n < 50) для оценки соответ-
ствия распределения результатов измерений нормальному закону может
быть использована статистическая функция. Для ее построения результаты
измерений выстраивают в вариационный ряд в порядке возрастания и вы-
числяют по формуле:
()
i
i
Fx
n1
=
+
. (7.18)
График этой функции представляет собой ступенчатую линию, каждая
ступенька которой равна 1/(n+1) и соответствует переходу к следующему члену
вариационного ряда. Если для некоторых значений
ii1 ik
xx ...x
+
+
=
==
, то в точ-
ке
(
)
ii1 i
xxFx
+
= возрастает на
1n
k
+
, где k — число равных между собой чле-
нов ряда.
Для проверки нормальности распределения результатов наблюдений вы-
числяют значения
i
t соответствующие значениям
(
)
(
)
ii
tFxF
=
по формуле:
2345
ii i ii
i
23 45
ii i i i
3,291 198b 1064,91b 1870,41b 1241,03b 234,37b
t
1 121,21b 157,53b 550,16b 1020,33b 435,11b
−− + − + −
=
+− − + −
, (7.19)
где
(
)
ii
b
Fx= .
Зависимости, определяемые выражениями (7.18) и (7.19), выбраны таким
образом, что колоколообразная кривая (гауссиана) в таких координатах преоб-
разуется в прямую линию.
Выразив переменную
i
t через результаты наблюдений
i
x как
i
i
xX
t
S
−
= ,
можно получить график с координатами
i
x и
i
t (рис. 7.3).
Рисунок 7.3 — Проверка нормальности распределения результатов наблюдений
91
Наиболее распространенной функцией распределения случайной по-
грешности, как отмечалось выше, является нормальная функция (функция
Гаусса). При обработке результатов наблюдений при априорно неизвестном
законе распределения случайных погрешностей проводят проверку
нормаль-
ности распределения
результатов наблюдений. Для этого используют методы
проверки статистических гипотез. Поскольку проверка статистических гипо-
тез основывается на опытных данных, то при принятии решения всегда воз-
можны ошибки.
Если отвергается
в действительности верная гипотеза, то совершается
ошибка первого рода. Вероятность ошибки первого рода называется уровнем
значимости q:q 1=−α, где α — вероятность правильного принятия верной
гипотезы.
Если принимается в действительности неверная гипотеза, то совершается
ошибка второго рода. В общем случае вычислить ее вероятность нельзя. Одна-
ко при уменьшении вероятности ошибки первого рода вероятность ошибки
второго рода
увеличивается, поэтому не имеет смысла выбирать слишком низ-
кий уровень значимости
q. Как правило, q принимают в пределах от 1 до 5 %.
Критерии проверки статистических гипотез приводятся в справочной ли-
тературе по теории вероятностей и в нормативных документах по метрологии, в
частности, в ГОСТ 8.207-76 (переиздан 01.08.2008) «ГСОЕИ. Прямые измере-
ния с многократными наблюдениями. Методы обработки результатов наблюде-
ний. Основные положения».
5.9 Суммирование составляющих погрешности измерений
Погрешности измерения обусловлены различными факторами, поэтому
суммарная случайная погрешность в общем случае может иметь несколько со-
ставляющих. Эту суммарную случайную погрешность можно оценить, проведя
многократные наблюдения. Однако на практике не всегда можно провести се-
рию многократных наблюдений. В этом случае предварительно оценивают зна-
чения математического ожидания и СКО каждой составляющей
погрешности, а
оценку суммарной погрешности находят расчетным путем.
Пусть имеется две составляющие случайной погрешности измерения.
Обозначив индексами «1» и «2» первую и вторую составляющие случайной по-
грешности, выразим их математическое ожидание и СКО следующим образом:
[]
1c1
M ∆=∆;
[
]
2c2
M ∆=∆;
0
11
∆
⎛⎞
σ
=σ ∆
⎜⎟
⎝⎠
;
0
22
∆
⎛⎞
σ
=σ ∆
⎜⎟
⎝⎠
.

92
В этом случае математическое ожидание суммарной погрешности:
[][][]
12 1 2 c1c2
MM MM
⎡⎤
∆=∆+∆=∆+∆=∆+∆
⎢⎥
∑
⎣⎦
. (5.51)
Дисперсия суммарной погрешности определяется следующим образом:
[]
()
[]
[]
2
2
12 12
22 2 2
12 12 1 2 12
00
22
12 12
DDM
M2MM2M
2M .
∆∆
⎡⎤
=σ = ∆ +∆ = ∆ +∆ =
⎣⎦
∑∑
⎡ ⎤ ⎡⎤ ⎡⎤
= ∆+∆+∆∆= ∆+ ∆+ ∆∆=
⎣ ⎦ ⎣⎦ ⎣⎦
⎛⎞ ⎛⎞
=σ ∆ +σ ∆ + ∆∆
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
(5.52)
Математическое ожидание произведения двух случайных величин (в
данном случае двух случайных погрешностей) называется
корреляционным
моментом
.
Корреляционный момент определяет степень «тесноты» линейной зави-
симости между погрешностями. Вместо корреляционного момента часто ис-
пользуют коэффициент корреляции:
12
12
0
0
M
r.
1
∆∆
⎡
⎤
∆∆
⎣
⎦
=
⎛⎞
⎛⎞
σσ
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∆
∆
(5.53)
Если погрешности
1
∆ и
2
∆ некоррелированные, то
12
r0
∆∆
= .
В случае, если СКО составляющих
1
∆
, и
2
∆
неизвестно, то оценки СКО
суммарной погрешности определяют по формуле:
121212
^
22
SSS2rSS
∆∆∆∆∆∆∆
=++
∑
. (5.54)
Здесь
1
S
∆
,
2
S
∆
— оценки СКО составляющих
1
∆
и
2
∆
:
()
i
1
n
2
11
1
S
n1
∆
∆−∆
=
−
∑
,
n
11i
1
1
n
∆
=∆
∑
; (5.55)
()
i
2
n
2
22
1
S
n1
∆
∆−∆
=
−
∑
,
i
n
22
1
1
n
∆
=∆
∑
; (5.56)
()
()
12
ii
12
n
^
11 2 2
1
1
r
SS
∆∆
∆∆
=∆−∆∆−∆
∑
. (5.57)
Если
12
r0
∆∆
>
0
21
>
∆∆
r
, то
1
∆ возрастает при увеличении
2
∆ ;
12
r0
∆∆
< , то
1
∆ уменьшается при увеличении
2
∆
;
113
затем сравнивается с теоретическими значениями параметров
1
q
,n
2
d и
1
q
1,n
2
d
−
, ко-
торые берутся из вышеуказанного ГОСТа или рассчитываются по следующим
формулам.
Для
1
q/2 0,01= :
1
q
23
,n
2
2,13613163 16,7309022 67,92579337
d 0,828947791
nn n
=+++ ; (7.12)
1
q
1,n
2
62
2
d 0,761106099 0,000285516n
0,46816419 2,346065907
1, 4553 10 n
nn
−
−
=+ −
−⋅− +
. (7.13)
Для
1
q/2 0,05= :
1
q
23
,n
2
0,646423899 11,7275535 45,89795165
d 0,82006805
nn n
=+ ++ ; (7.14)
1
q
1,n
2
62 73
d 0,690817475 0,002664875n
4,2945 10 n 2,77441 10 n
−
−−
=+ −
−⋅+ ⋅
. (7.15)
Для
1,02/q
1
=
:
1
62
q
,n
2
2
d 0,865918409 0,00105608n 7,81398 10 n
0,297075609 0,926160028
;
nn
−
=−+⋅+
++
. (7.16)
1
62
q
1,n
2
2
d 0,735411585 0,000367873n 1,0371 10 n
1.23607266 4.904457538
...
nn
−
−
=+ −⋅−
−+
(7.17)
Гипотеза о нормальности по первой части составного критерия d прини-
мается, если выполняется условие:
11
qq
1,n ,n
22
ddd
−
≤
≤ .
В противном случае гипотеза о нормальном законе распределения ре-
зультатов измерения отвергается.
Вторая часть составного критерия введена для проверки так называемых
концов распределения. Предполагается, что распределение результатов наблю-
дения соответствует нормальному закону, если не более m разностей
i
xX
−
превзойдет значение
px
tS, где
p
t — квантиль распределения нормированной
функции Лапласа (коэффициент Стьюдента).
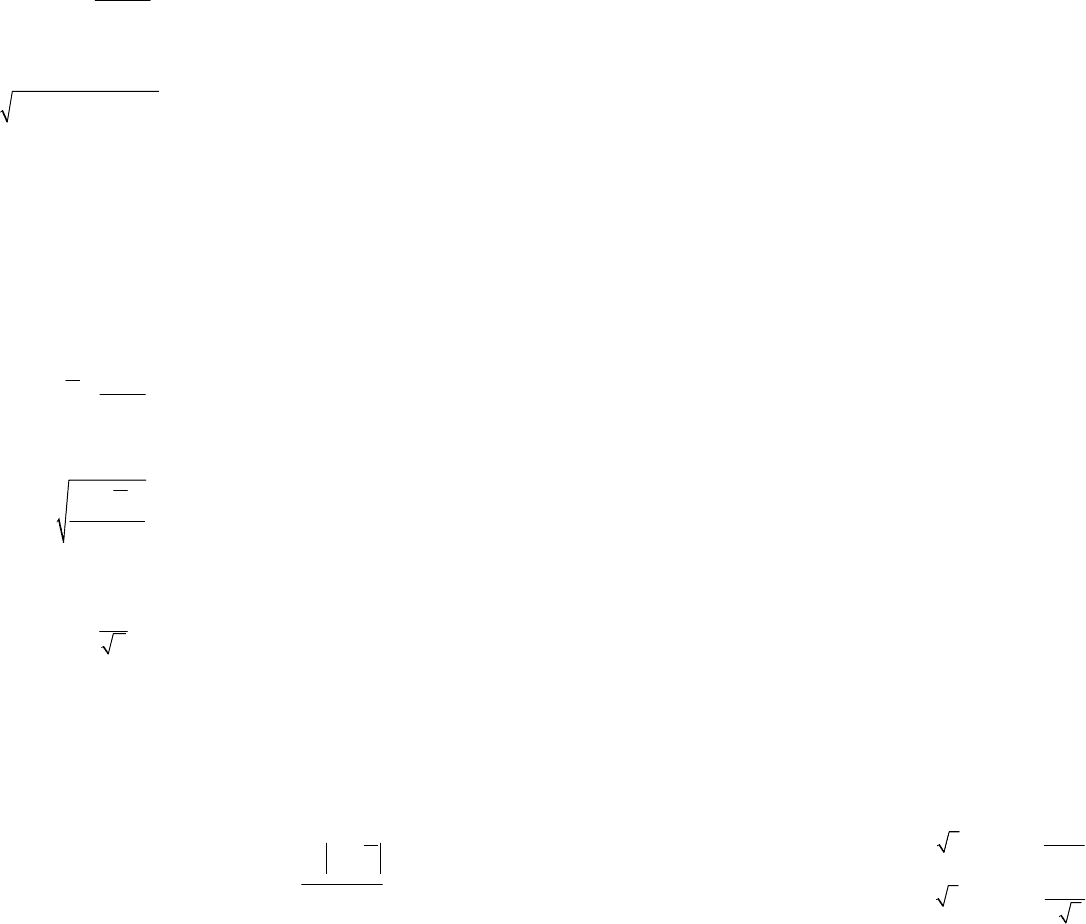
112
Для исключения погрешностей должно выполняться условие:
k
222
S 1,1025(S S )
ΘΘΘ
<−,
k
22
0,1025
SS
1,1025
Θ
Θ
<
или
k
2
S0,3S
Θ
Θ
<
. (7.7)
Это условие легко распространяется на случай нескольких составляю-
щих, которыми можно пренебречь:
12 k
22 2
S S ... S 0,3S
ΘΘ Θ Θ
+++< . (7.8)
Если обнаружена систематическая погрешность и определен закон ее
распределения, то для ее исключения вводятся поправки с обратным знаком в
полученный ряд результатов измерений.
Введя поправку
ii
ν=−Θ, в каждый результат измерения, получим так на-
зываемый исправленный ряд результатов измерений
12 i
X ,X , ...,X , где
0
i
X
=
∆ ,
поскольку предполагается, что грубые погрешности уже исключены.
Затем вычисляют среднее арифметическое значение результатов измерений:
in
i
i1
X
X
n
=
=
=
∑
. (7.9)
После этого вычисляют оценку среднеквадратичного отклонения резуль-
тата измерений по формуле:
()
2
i
xX
n1
−
σ=
−
. (7.10)
Далее выполняют оценку среднеквадратичного отклонения среднего
арифметического значения:
x
n
σ
σ= . (7.11)
В случае, если число измерений n15
≤
, принимается нормальный закон
распределения результатов измерений и СКО. При n > 50 осуществляют про-
верку принадлежности этих параметров к нормальному закону с помощью кри-
терия
2
ω или
2
χ .
Если 15 n 50<≤ , то обычно используют составной критерий (ГОСТ 8.207-76),
сущность которого состоит в том, что в первой его части на основании экспери-
ментальных данных определяется значение параметра
in
i
i1
x
xX
d
nS
=
=
−
=
∑
, которое
93
12
r0
∆∆
= , то СКО суммарной погрешности определяется как сумма СКО
первой и второй составляющей
12
∆
∆
σ
=σ +σ
∑
;
12
r1
∆∆
=− , то СКО суммарной погрешности определяется, как разность
СКО первой и второй составляющих,
12
∆
∆
σ
=σ −σ
∑
.
Суммарная погрешность имеет m составляющих, то её дисперсия имеет
вид:
jkjkj
mm
22
j1 k1
j1
2r
∆∆∆∆∆∆
==
=
σ=σ+ σσ
∑
∑∑
. (5.58)
5.10 Точечная и интервальная оценки истинного значения
измеряемой физической величины
Все бесконечное число значений результатов измерений детерминиро-
ванной физической величины называется генеральной совокупностью. На прак-
тике же всегда имеют дело с ограниченным числом наблюдений или измере-
ний, т. е. имеют дело с выборкой из генеральной совокупности, поэтому оценку
точности измерений проводят по ограниченному, хотя иногда и довольно
большому, числу наблюдений.
В результате получают одно число. Это называ-
ется точечной оценкой.
Задача получения точечных оценок результатов измерений и СКО слу-
чайных погрешностей является частным случаем статистической задачи нахо-
ждения оценки параметров функции распределения случайной величины на ос-
новании выборок, т. е. ряда значений, принимаемых этой случайной величиной
в ограниченном числе n независимых опытов
.
Независимо от закона распределения случайной величины, оцениваемы-
ми параметрами являются математическое ожидание и СКО функции распреде-
ления. Сами же формулы для оценок имеют различный вид в зависимости от
закона распределения плотности вероятности. Для нормального закона в фор-
мулы для дифференциальной функции распределения математического ожида-
ния (m
x
) и СКО (
x
σ ) входят в явном виде, а для равномерного распределения
определяются выражениями:
xx
b
m3=+σ;
x
ab
m
2
+
= ;
xx
am 3=−σ ;
x
b
a
23
−
σ=
.

94
Если есть параметр А, то его оценка A называется точечной, если она
выражается одним числом.
Любая точечная оценка, вычисленная на основании опытных данных, бу-
дучи их функцией, сама является случайной величиной с распределением, зави-
сящим от трех факторов:
— закона распределения исходной случайной величины;
— самого оцениваемого параметра;
— числа опытов n.
К оценкам предъявляются следующие требования.
1
. Состоятельность. Оценка считается состоятельной, если с увеличени-
ем числа опытов n она приближается (сходится по вероятности) к значениям
оцениваемого параметра, т. е.
{
}
^
n
lim P A A 1
→∞
=
= .
2.
Несмещенность. Оценка называется несмещенной, если ее математи-
ческое ожидание равно оцениваемому параметру:
^
MA A
⎡⎤
=
⎢⎥
⎣⎦
.
3.
Эффективность. Оценка называется эффективной, если ее дисперсия
меньше дисперсии другой оценки данного параметра.
Выясним, что значат разные оценки одного и того же параметра.
Предположим, что имеется упорядоченный или вариационный ряд ре-
зультатов наблюдений случайной величины X:
12 i n
X , X ,..., X ,..., X
.
Вариационный ряд — ряд, в котором последующее значение больше
(равно) предыдущего
12ii1n
(X X ,...,X X X )
+
≤≤≤ или меньше (равно) пре-
дыдущего.
Можно провести оценки параметра различными методами: по медиане,
по размаху, по среднему арифметическому и др.
Оценка по медиане. Как отмечалось ранее, медиана Ме[Х] — центральное
среди результатов наблюдений значение случайной величины в упорядоченном
ряду результатов наблюдений. В случае, если имеется четное число наблюде-
ний:
[]
()
(
)
n/2
n/2 1
Me X 0,5 X X
+
=+
.
В случае, если n нечетное число:
[
]
()
n/2 1
Me X X
+
=
.
Например: при n = 3 Ме[Х] = Х
2
; при n = 4 Ме[Х] = 0,5(Х
2
+ Х
3
).
111
— погрешности, связанные с колебанием влияющих величин при невоз-
можности их контроля и учета поправок;
— методические или теоретические погрешности;
— погрешности, связанные с округлением при снятии показаний СИ;
— погрешности поверки и калибровки средств измерений.
Для каждого данного измерения не исключенные остатки систематиче-
ской погрешности имеют вполне определенные значения, но эти значения
нам
неизвестны. Известно лишь, что в массе однократных измерений эти остатки
лежат в определенных границах ±
kmax
Θ
или имеют определенное среднеквад-
ратичное отклонение, не превышающие
k
S
Θ
, где к — номер не исключенной
составляющей систематической погрешности. Если закон распределения не
исключенной систематической погрешности неизвестен, то для самих систе-
матических погрешностей
k
Θ принимают равномерный закон распределения,
а для
k
S
Θ
— нормальный. Дисперсия суммы не исключенных остатков систе-
матической погрешности определяется как сумма дисперсий не исключенных
остатков:
[]
12112
j
mmmmm
22 2 2
kmax k
k1 k2 j1
1
DQ S S
3
=+
ΘΘ
===
== Θ +Θ=
∑∑∑
, (7.4)
где m
1
— число систематических погрешностей, заданных границами ±
kmax
Θ ;
m
2
— число систематических погрешностей, заданных СКО
k
S
Θ
.
Не все составляющие НСП играют одинаковую роль или вносят одинако-
вый вклад в суммарную НСП. Отдельные составляющие вносят пренебрежи-
тельно малый вклад в суммарную погрешность, и ими можно пренебречь.
Пользуясь правилами округления и учитывая, что погрешность выражается не
более чем двумя значащими цифрами, следует ввести такое условие, при кото-
ром
можно пренебречь к-й составляющей НСП:
k
k
m
2
j1
jk
S1,05 S
Θ
Θ
=
≠
<
∑
, (7.5)
где
j
m
22
j1
SS
ΘΘ
=
=
∑
— суммарная погрешность результата измерения; значение 1,05
получено из условия округления 1,049999...;
kk
m
222
j1
jk
SSS
Θ
ΘΘ
=
≠
=−
∑
. (7.6)
