Новосельцева Т.А., Корепанова В.С. Метрология

Подождите немного. Документ загружается.

— возможность выделения измеряемой величины среди других величин;

— возможность установления единицы, необходимой для измерения вы-

деленной величины;

— возможность материализации (воспроизведения и хранения) установ-

ленной единицы применяемыми техническими средствами;

— возможность сохранения неизменным размера единицы измеряемой

величины (в пределах приписанной точности) как минимум на срок, необходи-

мый для выполнения измерения.

Для удобства

изучения, анализа и практического применения целесооб-

разно классифицировать все измерения по признакам. Эта классификация мо-

жет основываться на следующих основных признаках измерений:

— по характеру проявления измеряемой величины на результат

измерения;

— по способу получения результата измерения;

— по точности получаемых результатов измерения;

— по характеру представления результатов измерения;

— пo методу измерения

;

— по числу измерений;

— по принципу измерения;

— по методу измерения:

— по числу измерений:

— по характеристике точности получаемых результатов измерений;

Предложенная классификация измерений представлена на рисунке 3.2

Измеряемая физическая величина в соответствии с конкретной измери-

тельной задачей может быть принята за неизменную в течение времени измере-

ния. В этом случае измерения

называют статическими измерениями. Если в

процессе измерений размер физической величины изменяется, то они называ-

ются

динамическими измерениями. В некоторых случаях измерения даже по-

стоянной во времени физической величины могут быть классифицированы как

динамические, если в процессе измерений происходит какой-то переходный

процесс. Например: процесс колебания чаши весов, на которую положена гиря

определенной массы. Особенностью динамических измерений является то, что

здесь необходимо учитывать динамическую погрешность.

В зависимости от

способа получения результатов измерений измерения

могут быть отнесены к одному из видов измерений: прямые, косвенные, сово-

купные и совместные.

измерительного преобразования. Поэтому эти величины не измеряют, а оце-

нивают по заранее выбранным правилам в порядке убывания или возрастания

размера величины.

Оценивание может осуществляться двумя способами.

Во-первых, может быть использована

условная шкала с нанесенными на

нее опорными (реперными) точками. К таким шкалам, например, относится

шкала Мооса для определения твердости минералов, которая содержит десять

опорных минералов с условными числами твердости: 1 — тальк, 2 — гипс, 3 —

кальций, 4 — флюорит, 5 — апатит, 6 — ортоклаз, 7 — кварц, 8 — топаз, 9 —

корунд, 10 — алмаз. Отнесение минерала к той или иной степени твердости

осуществляется на основании царапания испытуемого

материала опорным. Ес-

ли после царапания кварцем (7) на нем остается след, а после царапания орток-

лазом (6) — не остается, то твердость испытуемого материала составляет более

6, но менее 7. Более точный ответ в этом случае дать невозможно.

Во-вторых, может быть подобрано измерительное преобразование, пере-

водящее размер изучаемой величины в некоторую совокупность размеров

ве-

личин первой группы, числовые значения которых и принимают за числовые

значения данной величины.

Например, твердость по шкале Бринелля определяют, вдавливая стальной

закаленный шар в образец с определенным усилием, а числовое значение твер-

дости рассчитывают как отношение этого усилия к площади отпечатка на ис-

пытуемом материале. Аналогично определяют твердость по шкале

Виккерса, но

вместо стального шарика в образец вдавливают алмазную пирамидку.

Как уже отмечалось, линейность преобразований величин третьей группы

проверить нельзя. Можно лишь утверждать, что их числовые значения связаны

друг с другом некоторым монотонным преобразованием.

1.3 Шкала интервалов (шкала разностей)

Измерительные шкалы интервалов применяют для измерений интервалов

величин второй группы, которые, в отличие от самих величин, удовлетворяют

отношениям эквивалентности, порядка и аддитивности (от лат. Additives —

прибавляемый, свойство величин, состоящее в том, что значение величины, со-

ответствующее целому объекту, равно сумме значений величин, соответст-

вующих его частям, каким бы образом ни был разбит

объект). Шкала интерва-

лов состоит из одинаковых интервалов и, как следствие, линейна и имеет еди-

ницу измерения. Ноль такой шкалы принят по соглашению, поэтому является

условным.

К таким шкалам относится: летоисчисление по различным календарям, в

которых за нулевую отметку принимается либо Рождество Христово, либо со-

творение мира; температурные шкалы Цельсия, Фаренгейта, Реомюра.

Так, во введенной Фаренгейтом температурной шкале первой опорной

точкой и началом отсчета служила температура

смеси льда, поваренной соли и

нашатыря (как наиболее низкая температура, которую можно было достаточно

точно воспроизвести в то время), а в качестве второй опорной точки была вы-

брана температура человеческого тела. Единица температуры определялась, как

одна девяносто шестая часть полученного таким образом основного интервала,

и была названа градусом Фаренгейта (°F). Температура

таяния льда оказалась

равной 32 °F, а температура кипения воды — 212 °F.

В температурной шкале Цельсия началом отсчета является температура

таяния льда, второй опорной точкой служит температура кипения воды, а за

единицу температуры принят градус Цельсия (°С), или одна сотая часть основ-

ного интервала.

В шкале измерения времени единица измерения воспроизводится непо-

средственно как интервал

времени, начало отсчета выбирают каждый раз по-

разному в зависимости от конкретных условий изучаемого явления и часто

просто связывают с началом этого явления.

Аналогично строится шкала для измерения электрических потенциалов.

В общем случае размер Q физической величины второй группы может

быть определен по шкале интервалов на основании уравнения:

[

]

QqQQ

где

Q — начало отсчета;

[]

Q — единица измерения; q — числовое значение

величины.

1.4 Шкала отношений

Физические шкалы отношений являются наиболее совершенными из всех

перечисленных, так как имеют не только единицу измерения, но и естествен-

ный ноль шкалы. Размер величины Q

может быть описан уравнением:

[

]

QqQ

С помощью этих шкал измеряются физические величины первой группы,

для которых справедливы отношения эквивалентности, порядка и аддитивно-

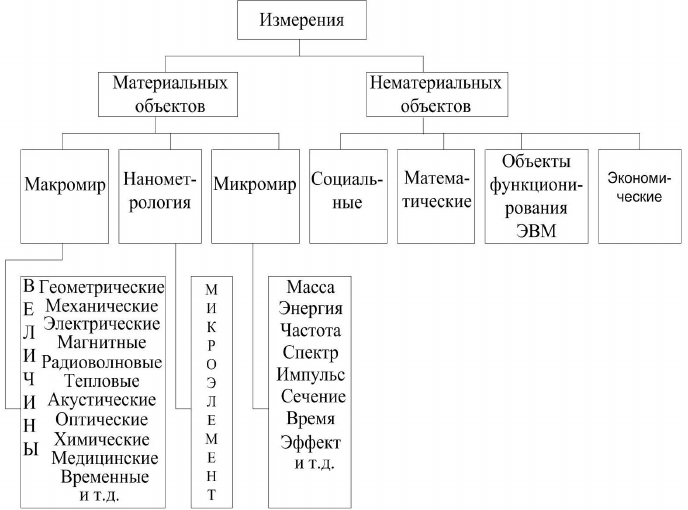
Рисунок 3.1 — Иерархическая схема объектов измерений

В математике общепризнанны понятия «измеримое множество», «мера» и

т. п., хотя, разумеется, ни о каких материальных средствах измерений здесь не

может идти речи. Для оптимизации вычислительного процесса на ЭВМ исполь-

зуют специальные встроенные измерительные программы

[

]

5. В этой области

предложен даже особый термин «компьюторометрика». В экономике имеет ме-

сто раздел эконометрика. В социологии имеются предложения, как измерить

уровень жизни населения страны и т. п. По-видимому, исключать эти немате-

риальные сущности из области применения понятия «измерение» было бы не-

верным, поэтому, данный термин должен иметь два

значения: в широком

смысле данного понятия и в узком — только для материальных объектов.

3.2 Измерения, их классификация

Цель измерения может быть достигнута (решена измерительная задача)

только в том случае, если для выполнения измерений будут созданы опреде-

ленные условия. К ним относятся:

1) измерение (в обычном классическом понимании) всегда выполняется с

помощью каких-либо специальных измерительных материальных средств;

результат измерения всегда получается в виде числа (совокупности чи-

сел, функции или графика), т. е. в виде определенного элементарного информа-

ционного объекта. Последний воспринимается либо непосредственно челове-

ком, либо передается какому-либо агрегату (активный контроль, информацион-

но-измерительная система и т. д.);

в результате измерения определяются количественно (изредка — каче-

ственно) какая-либо характеристики или свойства измеряемого объекта.

На основании выше изложенного представляется возможным дать общую

иерархическую схему объектов измерений (рис. 3.1).

Согласно рис. 3.1 все измеряемые объекты делятся на две категории: ма-

териальные и нематериальные. Первая из них состоит из трех классов: объекты

макромира (

в том числе классической физики), объекты нанометрологии и объ-

екты микромира (квантовые).

Первый класс в количественном и качественном отношениях пред-

ставляет собой основу всего комплекса, охватываемого понятием «измере-

ние». Количество средств измерений, обслуживающих данный класс исчис-

ляется миллиардами. Измеряемые в данном классе физические величины и

технические параметры делятся на группы: механические

, электрические,

магнитные и т. п.

Второй класс охватывает изделия, получаемые сугубо специфическими

методами нанотехнологии. Данное направление поучило развитие недавно, но

его значимость уже огромна. Вся современная вычислительная техника базиру-

ется на элементной базе, создаваемой такой технологией, где размеры деталей

порядка десятых долей микрометра.

Третий класс содержит измеряемые параметры объектов микромира,

точ-

нее, квантовые объекты. Измерение имеет весьма существенную специфику,

поэтому их совокупность образует свой особый класс. Следует отметить, что

многие из соответствующих данному классу средства измерений представляют

собой установки высшей степени сложности и точности.

Что же касается нематериальных объектов, то здесь нет единого мнения —

применим ли к ним термин «измерение». Переоценим

некоторые из таких

объектов.

сти, определены все арифметические операции: сложение, вычитание, умноже-

ние и деление, что имеет важное значение для измерения этих величин.

Из приведенного уравнения следует, что числовое значение величины

первой группы показывает, во сколько раз значение измеряемой величины

больше некоторого значения, принятого за единицу, и это числовое значение q

зависит от размера принятой единицы.

Примерами величин, для которых существуют шкалы отношений, явля-

ются: масса, длина, термодинамическая температура, связанная со шкалой

Кельвина, сила электрического тока, электрическое напряжение и т. д. Дейст-

вительно, складывая две массы

m и

m, получим в результате физически то

же свойство — массу с размером

m, причем

213

mmm

1.5 Абсолютные шкалы

Иногда для физических величин, для которых справедливы отношения

эквивалентности, порядка и аддитивности, но дополнительно имеющих есте-

ственное определение единицы измерения, не зависящее от принятой систе-

мы единиц, используют понятие

абсолютных шкал. Эти шкалы обладают

всеми признаками шкал отношения, но при этом имеют безразмерную еди-

ницу измерения. Это относительные величины, такие как коэффициенты

усиления, ослабления, плоский или телесный угол и т. д. Введение таких ве-

личин объясняется удобством выражения некоторых физических процессов

или явлений, их математического описания и практической реализации в из-

мерительной технике.

2 Международная система единиц SI

Единицы физических величин появились в тот момент, когда у человека

возникла необходимость выразить что-то количественно. Сначала единицы фи-

зических величин выбирались произвольно, без какой-либо связи друг с дру-

гом, что создавало значительные трудности. По мере развития техники и меж-

дународных связей использование результатов измерений, выраженных в раз-

личных

единицах, осложняло и тормозило дальнейшее развитие науки и техни-

ки. Возникла необходимость в создании единой системы единиц физических

величин.

Под

системой единиц ФВ понимается совокупность основных единиц

ФВ, выбираемых независимо друг от друга, и производных единиц ФВ, кото-

рые получаются из основных на основании физических зависимостей.

Впервые понятие системы единиц ввел немецкий ученый К. Гаусс. Он

предложил принцип построения таких систем. По этому принципу вначале ус-

танавливают или выбирают несколько физических величин, независимых друг

от друга. Единицы этих физических величин называются

основными, так как

они являются основой для построения всей системы единиц других величин.

Метод, основанный на этом принципе, имеет следующие особенности:

— не связан с конкретными размерами основных единиц величин;

— построение системы единиц возможно для любых величин, между ко-

торыми имеется связь, выражаемая в математической форме в виде уравнения;

— выбор величин,

единицы которых должны стать основными, ограни-

чивается соображениями рациональности и в первую очередь тем, что опти-

мальным является выбор минимального числа основных единиц величин.

Первоначально была создана система единиц, основанная на трех едини-

цах: длины, массы, времени (сантиметр, грамм, секунда) (СГС).

Наиболее распространенная и принятая в России Международная система

единиц (сокращенное

обозначение СИ) содержит семь основных единиц и две

дополнительные. Основные единицы ФВ системы СИ приведены в таблице 2.1.

Таблица 2.1 — Основные единицы физических величин системы СИ

Физическая величина Размерность Наименование единицы Обозначение

1 2 3 4

Длина L метр м

3 Виды и методы измерений

3.1 К понятию термина «измерение»

Понятие «измерение», является одним из основных в метрологии. Поэто-

му понятно, то внимание, которое уделяется в настоящее время его анализу и

трактовке. Число предложенных определений его превысило два десятка и про-

должает расти. Особую значимость данный вопрос приобрел в квантовой меха-

нике, где термин «измерение» приобрел иное, новое звучание. Свидетельством

тому являются изыскания в этой области А. Эйнштейна, Н. Бора, Дж. фон Ней-

мана и многих других великих физиков XX века.

Все формулировки и определения термина «измерение» можно разбить (и

объединить) на несколько взаимно непересекающихся групп.

Измерение — это:

— нахождение значения физической величины или технического пара-

метра опытным путем с помощью специальных материальных средств;

— познавательная процедура, выполняемая с помощью специальных

средств;

— особый вид информационного процесса, целью которого является по-

лучение количественной (как правило) информации о измеряемом объекте;

— отображение свойств объекта на пространство информативных (для

человека или

машины) образов.

Данные формулировки имеют общий характер — они справедливы для

измерений как макро-, так и микрообъектов. Но для последних были предложе-

ны другие, специальные определения.

Измерение — это:

— нахождение опытным путем собственных значений оператора А, опи-

сывающего измеряемый квантовый объект;

— сведения спектрального разложения волновой функции

() ()

qcq

ВВn

ψ=ϕ

∑

к одной функции

(

)

— «стягивание волновой

функции».

Необходимо отметить, что измерение — материальный процесс, а функ-

ция

()

qψ

только описывают его, поэтому оно не может сводиться только к на-

хождению функций.

Несмотря на многообразие трактовок понятия «измерение», они содержат

общие моменты, выделяющие его в особую, самостоятельную категорию. К

этим «общим» можно отнести следующие моменты:

Под воспроизведением единицы физической величины понимается точное

(в пределах допустимой погрешности) возобновление числового значения дан-

ной единицы соответствующим средством измерения.

Хранение воспроизведенного значения единицы физической величины —

сохранение воспроизведенной единицы физической величины без изменения в

течение заданного периода времени.

Воспроизведение, хранение и передача размеров единиц ФВ осуществля-

ется с помощью эталонов. Высшим звеном в цепи передачи размеров единиц

ФВ являются эталоны. Основное назначение эталонов — обеспечение матери-

ально-технической базы воспроизведения и хранения

единиц ФВ.

Окончание табл. 2.1

1 2 3 4

Масса M килограмм кг

Время T секунда с

Сила электрического тока I ампер А

Термодинамическая

температура

Θ кельвин К

Количество вещества N моль моль

Сила света J кандела кд

Дополнительные единицы СИ:

плоский угол

— радиан (рад) — угол между двумя радиусами окружности,

длина дуги между которыми равна радиусу;

телесный угол — стерадиан (ср) — телесный угол с вершиной в центре

сферы, вырезающий на поверхности сферы площадь, равную площади квадрата

со стороной, равной радиусу сферы.

Производные единицы СИ образуются с помощью простейших уравне-

ний связи между величинами и, поскольку эта система когерентна, К

= 1.

В этой системе размерность производной ФВ в общем виде определится

следующим образом:

[][][ ]

[

]

[

]

[

]

[

]

[

]

QLMTI JN

γβ

δεωλ

=Θ, (2.1)

где [L], [М ]

и т. д. — см. таблицу 2.1;

λωεδγβα ,,,,,, — целые положительные или отрицательные числа, включая 0.

Например, размерность единицы скорости в СИ:

[][][]

[

]

[

]

[

]

[

]

[

]

[

]

[

]

110000101

TLNJITMLМ

−−

=Θ= .

Так как данное выражение для размерности производной ФВ в СИ совпа-

дает с уравнением связи между производной ФВ и единицами основных ФВ, то

удобнее пользоваться выражением для размерностей:

LTV

−

Подобным образом можно получить любую производную величину сис-

темы СИ.

Систему СИ устанавливает ГОСТ 8.417-2002 «ГСОЕИ. Единицы вели-

чин».

Основные преимущества системы СИ:

1) универсальность — охватывает все области науки и техники;

2) унификация единиц для всех видов измерений;

3) удобство применения основных и большинства производных единиц;

4) когерентность — коэффициент пропорциональности в физических

уравнениях, определяющих единицы производных ФВ, равен 1;

5) упрощение записи уравнений и формул из-за отсутствия в них пере-

водных коэффициентов.

Таблица 2.2 — Производные единицы СИ

Величина Размерность

Обозначение

единицы

Частота периодического

процесса

-1

Гц

Сила LMT

-2

Плотность L

-3

M кг/м

Энергия L

-2

Дж

Определения основных единиц системы СИ.

Метр равен 1 650 763,73 длины волны в вакууме излучения, соответст-

вующего переходу между уровнями 2р

и 5d

атома криптона — 86.

Килограмм равен массе международного прототипа килограмма.

Секунда равна 9 192 631 770 периодам излучения, соответствующего пе-

реходу между двумя сверхтонкими уровнями основного состояния атома це-

зия — 133.

Ампер равен силе неизменяющегося тока, который при прохождении по

двум параллельным прямолинейным проводникам бесконечной длины и ни-

чтожно малой площади кругового поперечного сечения, расположенным в ва-

кууме на расстоянии 1 м друг от друга, вызвал бы на каждом участке провод-

ника длиной 1 м силу взаимодействия, равную

102

−

⋅

Н.

Кельвин равен 1/273,16 части термодинамической температуры тройной

точки воды.

Температура тройной точки воды — температура точки равновесия

воды в твердой (лед), жидкой и газообразной (пар) фазах на 0,01 К или 0,01 °С

выше точки таяния льда.

Допускается применение шкалы Цельсия. Температура в градусах (°С)

обозначается буквой t:

t = Т –Т

, где Т

= 273,15 К, тогда t=0°С при Т = 273,15 К.

Моль равен количеству вещества системы, содержащей столько же струк-

турных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.

Кандела равна силе света в заданном направлении источника, испускаю-

щего монохроматическое излучение частотой

10540

⋅

Гц, энергетическая сила

света которого в этом направлении составляет 1/683 Вт/ср.

Кроме системных единиц СИ применяют и некоторые внесистемные еди-

ницы, традиционно используемые в России: атмосфера, бар, миллиметр ртутно-

го столба; ангстрем; киловатт-час; час; дюйм и др.

Кроме того, применяют единицу логарифмической величины Бел (Б) —

логарифм (десятичный или натуральный)

безразмерного отношения одноимен-

ных ФВ. Логарифмические ФВ используют для выражения звукового давления,

усиления, ослабления. 1 Б = lg (Р

/Р

) при Р

= 10Р

где Р

и Р

– одноимённые энергетические величины (мощность, энергия).

Для силовых величин (напряжение, сила тока, давление, напряжённость

поля) Бел определяется как 1 Б = 2lg F2/F1 при

А10А =

Если Р

= 10Р

, то lg (Р

/Р

) = 10 дБ,

Если Р

= 10

, то lg (Р

/Р

) = 20 дБ и т. д.

Широко применяются относительные ФВ — отношения двух одноимён-

ных ФВ, которые выражаются в процентах (%).

Существуют правила написания обозначений единиц. При обозначении

производных единиц обозначения единиц, входящих в производные, разделя-

ются знаком умножения, например: H·м (ньютон-метр),

мA

⋅

(ампер — метр в

квадрате), Н с/м

(ньютон-секунда на метр в квадрате). Предпочтительнее

дробное выражение (м

/с), чем выражение в виде произведения единиц, возве-

денных в соответствующую степень (м

· с

-1

При произведении единиц с кратными или дольными приставками реко-

мендуется присоединять приставку к наименованию первой единицы, входя-

щей в произведение, например: 10

Н · м-кН · м — килоньютон-метр.

Единство измерений — это такое измерение, при котором результаты вы-

ражаются в узаконенных единицах, а их погрешность известна с заданной веро-

ятностью.

Для обеспечения единства измерений необходима тождественность еди-

ниц, в которых проградуированы все единицы СИ. Это достигается путем точ-

ного воспроизведения и хранения усыновленных единиц ФВ.

Тождественность единиц физических величин — свойство, характери-

зующее отношение между значениями единиц одноименных физических вели-

чин, рассматриваемое как одно и то же. Предельный случай тождественности —

равенство.

Систематическая погрешность возникает из-за несовершенства метода

измерения, систематических погрешностей системы измерения, неточной ма-

тематической модели измерений, влияния условий, погрешностей градуировки

и поверки СИ, человеческого фактора.

В большинстве случаев систематические погрешности можно изучить до

проведения измерений и в процессе измерения внести соответствующие по-

правки. Наиболее предпочтительны такие методы измерения, при которых

воз-

можно полное устранение причины систематической погрешности или в боль-

шей степени.

Случайная погрешность измерения — составляющая погрешности изме-

рений, имеющая случайный характер по знаку и значению при ряде одинако-

вых измерений одной и той же детерминированной ФВ.

Так, случайная погрешность при линейных и угловых измерениях обу-

словлена следующими причинами:

— неточность (перекос) установки СИ (рулетки, линейки, весов и т. п.);

— неточность установки начала отсчета;

— изменение

угла наблюдения;

— усталость глаз;

— изменение освещенности.

Случайная погрешность не может быть устранена до начала проведения

измерений, поскольку ее возникновение обусловлено случайными факторами.

Ее можно только уменьшить путем увеличения числа повторных измерений.

В основе обработки случайных погрешностей лежат теория вероятностей

и теория математической статистики.

Грубой погрешностью измерения (промахом) является такая погреш-

ность, значение которой значительно превышает ожидаемые значения система-

тической или случайной погрешностей в данных условиях измерения.

Причинами этих погрешностей могут быть: грубые ошибки эксперимен-

татора, резкое и неожиданное изменение условий измерений, внезапная неис-

правность средства измерения и др.

В зависимости от измерительной задачи погрешности могут выражаться

абсолютных и относительных величинах.

Абсолютная погрешность — погрешность, выраженная в единицах изме-

ряемой величины (например, погрешность измерения объекта массой в 5 кг —

0,005 кг). Условное обозначение абсолютной погрешности —

∆ .

Относительная погрешность — отношение абсолютной погрешности к

действительному значению измеряемой ФВ является безразмерной величиной

В условиях автоматизации технологических процессов обработки деталей

и сборки узлов и агрегатов машин, повышения требований к производительно-

сти, точности и качеству обработки и при массовом производстве все большее

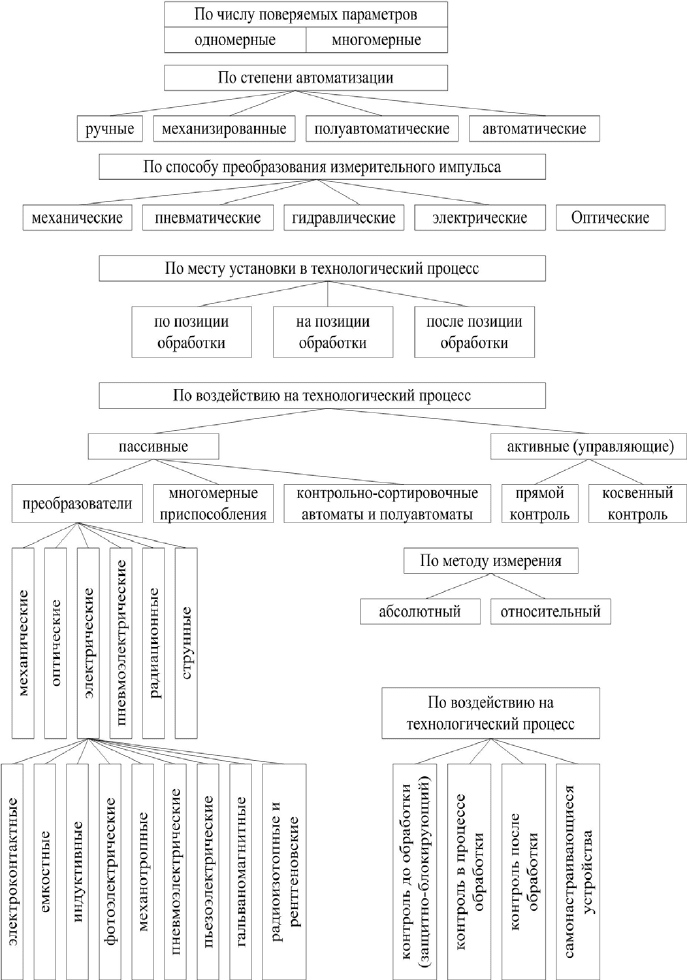
значение приобретали автоматические средства контроля, которые можно клас-

сифицировать по различным характеристикам (рис. 4.2).

4.3 Обобщенная структурная схема средств измерений

При изображении измерительных систем и отдельных средств измерений

применяют структурные схемы, в которых отдельные элементы изображаются

в виде блоков с указанием связей между ними и сигналами, характеризующими

физические величины.

Первичной задачей любого средства измерений является восприятие фи-

зической величины. Эту функцию выполняет чувствительный элемент.

Чувствительный элемент средства измерений — часть первого в изме-

рительной цепи преобразовательного элемента, находящаяся под непосредст-

венным воздействием измеряемой величины. Именно этот элемент определяет

способность средства измерений реагировать на изменения измеряемой вели-

чины. Основной задачей этого элемента является выработка сигнала измери-

тельной информации в форме, удобной для дальнейшей ее обработки. Этот

сигнал может быть механическим (

перемещение, поворот), пневматическим,

электрическим и др.

При использовании для измерений определенных физических явлений

возникает необходимость преобразовывать сигнал, полученный чувствитель-

ным элементом, в другую физическую величину (например, давление — в элек-

трическую величину, температуру — в давление и т. п.). Эту функцию выпол-

няет преобразовательный элемент.

Преобразовательный элемент средства измерений — элемент, в котором

происходит одно из ряда последовательных преобразований величины. Он

предназначен для выработки сигнала измерительной информации в форме

удобной для передачи, дальнейшего преобразования, обработки и (или) хране-

ния (например, преобразование неэлектрической величины в электрическую).

Как правило, эта информация не поддается непосредственному восприятию на-

блюдателем. Преобразовательный элемент может быть выделен

в отдельную

конструкцию, а может содержать два и более преобразователя. Преобразова-

тельный элемент, стоящий первым в измерительной цепи, обычно называют

первичным (например, термопара).

Рисунок 4.2 — Классификация автоматических средств контроля

Аббе, устранить просто. Принцип Аббе заключается в том, что при измерениях

линейных величин объект измерения и мера должны располагаться последова-

тельно. Погрешность, обусловленная неточностью изготовления средства изме-

рения, нельзя устранить полностью, так как невозможно абсолютно точно изго-

товить средство измерения.

Погрешности измерений условно можно разделить на четыре группы:

— погрешности, обусловленные

методами измерений (погрешность ме-

тода измерений);

— погрешности, возникающие из-за несовершенства самих средств изме-

рений;

— погрешности, связанные с особенностями органов чувств человека;

— погрешности, обусловленные условиями измерений.

Первая группа погрешностей обусловлена недостаточным знанием мате-

матической модели процесса измерения, пренебрежением некоторыми пара-

метрами или условиями информативного или неинформативного характера.

Под

погрешностью средства измерения понимают отклонение его пока-

зания (выходного сигнала) от значения измеряемой величины, воздействующей

на его вход.

Вторая группа погрешностей объясняется, с одной стороны, неточностью

изготовления средств измерения, а с другой — неточностью математической

модели метода измерения, на котором основано данное средство.

Погрешности зависят от многих причин, основной из них является опыт

оператора.

Четвертая группа погрешностей зависит как от внешних факторов (усло-

вия измерений), так и от внутренних (взаимные деформации объекта измерений

и чувствительного элемента средства измерения).

Эти погрешности проявляются одновременно и составляют

суммарную

погрешность измерения

. В общем случае суммарная погрешность измерения

содержит три различные составляющие: случайную, систематическую и грубую

погрешности измерений.

Поскольку точность измерения характеризуется случайной составляющей

суммарной погрешности измерений, а правильность — систематической, то

случайная погрешность измерения характеризует такое качество измерений,

как точность, а систематическая — правильность.

Под

систематической погрешностью измерения понимают составляю-

щую погрешности измерения, которая остается постоянной или закономерно

изменяется при повторных измерениях одной и той же детерминированной ФВ.

5 Погрешности измерений, их классификация

Теория измерений, являясь частью метрологии, базируется на таких раз-

делах математики, как теория вероятностей, математическая статистика, мате-

матический и регрессивный анализ и пр. Теория измерений занимается, с одной

стороны, обеспечением единства измерений, с другой стороны, получением

достоверной и надежной информации. Достоверность измерительной информа-

ции определяется точностью измерений, а надежность — правильностью

их

выполнения.

Мерой неопределенности результата измерений является погрешность

измерений.

Под

погрешностью измерений понимается отклонение результата изме-

рения от истинного значения измеряемой физической величины. Записывается

это следующим образом:

изм

−

∆ , (5.1)

где

∆

— погрешность результата измерения;

изм

X — результат измерения;

Q — истинное значение ФВ.

Однако поскольку истинное значение ФВ остается неизвестным, то неиз-

вестна и погрешность измерений, поэтому на практике имеют дело с прибли-

женными значениями погрешности или с так называемыми их оценками. В

формулу для оценки погрешности подставляют вместо истинного значения ФВ

действительное значение. Под

действительным значением ФВ

X понимается

значение, полученное опытным путем и настолько приближающееся к истин-

ному значению, что может быть использовано вместо него.

Таким образом, погрешность определяется по формуле:

дизм

−

∆

. (5.2)

Рассмотрим основные причины возникновения погрешностей измерений.

Их появление обусловлено различными факторами: условиями измерения, не-

совершенством конструкции средства измерения, неточностью математической

модели процесса измерения, несовершенством метода измерения, неточностью

изготовления средства измерения, субъективными погрешностями, неправиль-

ным взаимным расположением объекта и средства измерения и др. Некоторые

из них могут быть определены заранее

и сведены к минимуму или практически

полностью устранены, другие нельзя избежать в принципе. Например: погреш-

ность, возникающую из-за неправильного взаимного расположения объекта и

средства измерения при линейных измерениях, т. е. из-за нарушения принципа

Существует огромный класс промежуточных (вторичных) преобразовате-

лей, которые не меняют род физической величины. Широкое распространение

получили аналоговые, аналого-цифровые преобразователи (АЦП) и цифроана-

логовые преобразователи (ЦАП).

Для дистанционной передачи сигнала измерительной информации преду-

сматриваются передающие измерительные преобразователи, а для ее изменения

в заданное число раз — масштабные измерительные преобразователи. Напри-

мер: индуктивные

и пневматические преобразователи относят к передающим

преобразователям, а делители напряжений на входе вольтметров или электрон-

ных осциллографов, измерительные усилители относят к масштабным измери-

тельным преобразователям.

Измерительная цепь средства измерений — совокупность преобразова-

тельных элементов средства измерений, обеспечивающая осуществление всех

преобразований сигнала измерительной информации.

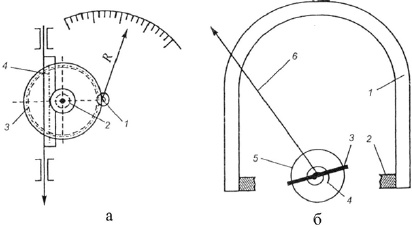
Измерительный механизм — часть конструкции средства измерений, со-

стоящая из элементов, взаимодействие которых вызывает их взаимное переме-

щение (рис. 4.3, а, б ).

Рисунок 4.3 — Пример измерительных механизмов:

а — индикатор часового типа (1-3 — зубчатые колёса; 4 — зубчатая рейка);

б — магнитоэлектрический измерительный прибор (1 — постоянный магнит;

2 — полюсный наконечник; 3 — подвижная рамка; 4 — пружина;

5 — сердечник; 6 — стрелка)

Отсчетное устройство средства измерений — часть конструкции сред-

ства измерений, предназначенная для отсчитывания значений измеряемой ве-

личины. Оно часто включает в себя шкалу и указатель. В самопишущих прибо-

рах отсчетное устройство осуществляет запись в виде диаграммы, в интегри-

рующем приборе чаще всего применяется счетный механизм.

Шкала представляет собой совокупность отметок или других символов,

соответствующих ряду последовательных значений не величин. Шкалы быва-

ют односторонними (рис. 4.4, а), двухсторонними (рис. 4.4, б ) и безнулевыми

(рис. 4.4, в). В односторонних шкалах один из пределов измерений средства

измерений равен нулю. В двухсторонних шкалах нулевое значение расположе-

но на шкале, в безнулевых — на шкале

нет нулевого значения.

Рисунок 4.4 — Шкалы: а — односторонняя; б — двусторонняя; в — безнулевая

В соответствии с ГОСТом 8.401—80 «ГСОЕИ. Классы точности средств

измерений. Общие требования»

практически равномерной шкалой называется

шкала, длина делений которой отличается друг от друга не более чем на 30 %, и

имеет постоянную цену делений.

Существенно неравномерная шкала — шкала

с сужающимися делениями, а

степенная шкала — шкала с расширяющимися

делениями, отличная от шкал, указанных выше.

Указатель — часть отсчетного устройства, положение которой относи-

тельно отметок шкалы определяет показание средства измерений. Указатель

может быть выполнен в виде стержня — стрелки (рис. 4.3) или может пред-

ставлять собой луч (света — световой указатель).

В показывающих приборах при наличии шкалы и указателя возможны

отсчетные устройства двух видов: указатель перемещается относительно не-

подвижной шкалы (

индикаторы часового типа, вольтметры, амперметры и др.);

шкала перемещается относительно неподвижного указателя (микрометры, оп-

тиметры и др.).

Цифровые отсчетные устройства бывают механические либо световые.

Механические отсчетные устройства используют в тех цифровых приборах, в

которых измеряемая величина преобразуется в

соответствующие углы поворота

валов (например, отсчетные устройства некоторых типов бензоколонок, прибо-

ры с цифровой лентой и цифровым роликом и др.).

зорезисторов ГСП категории точности 0,1, предназначенных для работы в диа-

пазоне температур ±50 °С:

Наименование

Значение характеристики в процентах

от номинального значения рабочего

коэффициента преобразования

Пределы допускаемой систематиче-

ской составляющей основной погреш-

ности

1,0

Пределы среднего квадратического

отклонения случайной составляющей

основной погрешности

05,0

Предел допускаемой вариации 0,1

Граничные функции влияния темпера-

туры окружающей среды на началь-

ный коэффициент преобразования

(

)

105 Θ−Θ⋅

−

Граничные функции влияния темпера-

туры окружающей среды на рабочий

коэффициент преобразования

(

)

105 Θ−Θ⋅

−