Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


[
]
[
]
[
]
[
]
[
]
[
]
[] [] [] []
kkZZjkYZikXZkjZY
jjYYijXYkiZXjiYXiiXXba
21212121
3121212121
×+×+×+×+
+×+×+×+×+×=×
Из этого равенства и соотношений (2) получаем разложение (1).
Следствие. Если два вектора
{
}
111
Z,Y,X=a и
{
}
222
Z,Y,Xb = коллинеарны, то их
координаты пропорциональны:
2
1
2
1
2
1
Z
Z
Y
Y
X
X
==
.
Доказательство. Из равенства нулю векторного произведения и из формулы 1
имеем
0ZYZY ,0XZXZ ,0YXYX
122112211221
=
−
=
−
=− , ч.т.д.
1.3.7. Смешанное произведение трех векторов
Пусть даны три вектора
c è b,a . Если вектор a векторно умножается на
вектор
b , а затем полученный вектор
[
]
ba × скалярно умножается на вектор c , то в
результате получается число
[
]
(
)
cba ⋅× , называемое смешанным произведением
векторов
c è b,a .
Из определения следует геометрический смысл смешанного произведения
трех векторв:
Смешанное произведение
[
]
(
)
cba ⋅× равно объему параллелепипеда,
построенного на приведенных к общему началу векторах
c è b,a , взятому со
знаком плюс, если тройка
c,b,a правая, и со знаком минус, если тройка c,b,a
левая. Если же векторы компланарны, то
[
]
(
)
0cba =⋅× .
c
b
a
Отсюда видно, что
[
]
(
)
[
]
(
)
cbacba ×⋅=⋅× .
Поэтому можно записать смешанное произведение трех векторов
c è b,a
просто в виде
(
)
[
]
(
)
cbacba ⋅×=
не указывая какие именно два вектора перемножаются векторно.
Следствие 1. Необходимым и достаточным условием компланарности трех
векторов является равенство нулю их смешанноно произведения.
Следствие 2.
(
)
(
)
cabcba ⋅⋅−=⋅⋅
1.3.8. Выражение смешанного произведения в декартовых координатах
Теорема. Если три вектора
c è b,a определены своими ДПК
{}
{
}
{
}
333222111
Z,Y,X=c ,Z,Y,X=b ,Z,Y,Xa = ,
то смешанное произведение
cba равно определителю, строки которого
соответственно равны координатам перемножаемых векторов:
()
333
222
111
ZYX
ZYX
ZYX
cba =

Доказательство. Т.к.
[
]
{}
{
}
333122112211221
Z,Y,X=c à ,YXYX ,XZXZ ,ZYZYba −−−=× ,
то скалярное произведение этих векторов равно
()
[
]
(
)
()
(
)
(
)
333
222
111
22
11
3
22
11
3
22
11
3
122132112312213
ZYX
ZYX
ZYX
YX
YX
Z
ZX
ZX
Y
ZY
ZY
X
YXYXZZXZXYZYZYXcbacba
=+−=
=−+−+−=⋅×=
ч.т.д.
Следствие. Необходимым и достаточным условием компланарности трех
векторов
{}{}{
333222111
Z,Y,X=– ,Z,Y,X=b ,Z,Y,Xa =
}
является равенство нулю определителя,
строками которого являются координаты этих векторов:
0
ZYX
ZYX
ZYX
333
222
111
=
.
1.4. Уравнение линии на плоскости
Пусть на плоскости π заданы декартова прямоугольная система координат
Oxy и некоторая линия L. Рассмотрим уравнение, связывающее переменные x и y
(
)
0y,x
=
Φ
(1.1)
Определение. Уравнение (1.1) называется уравнением линии L (относительно
заданной системы координат), если этому уравнению удовлетворяют координаты
x и y любой точки, лежащей на линии L, и не удовлетворяют координаты x и y ни
одной точки, не лежащей на линии L.
Т.е. линия L представляет собой геометрическое место точек, координаты
которых удовлетворяют уравнению (1.1).
Примеры. 1). Уравнение
()
(
)
2
22
rbyax =−+− является уравнением окружности
радиуса
с центром в точке 0 r〉
(
)
b,a
0
Μ .
2). Уравнение определяет на плоскости Oxy только одну точку
(0,0).
0yx
22
=+
3). Уравнение
вообще не определяет никакого геометрического
образа.
04yx
22
=++
1.4.1. Параметрическое представление линии
Для аналитического представления линии L возможно выражать
координаты x и y точек этой линии при помощи параметра t:
(
)
(
)
ty ,tx
ψ
ϕ
=
=
(2.1.)
где функции
()
(
)
t è t
ψ
ϕ
непрерывны по параметру t в области {t} изменения этого
параметра. Исключение из двух уравнений (2.1) параметра t приводит к
уравнению вида (1.1).
Пример. Найдем параметрические уравнения окружности радиуса r>0 с центром
в начале координат.
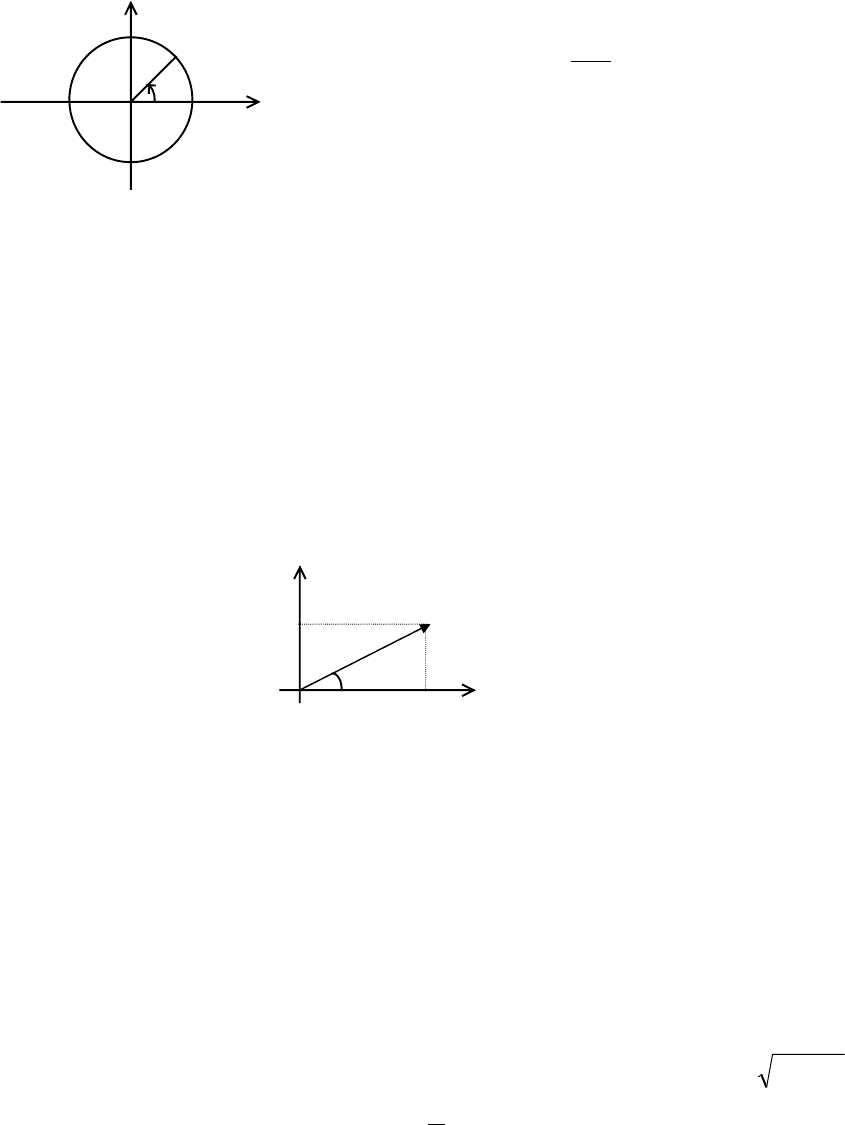
y
M
r
t
0 x
Пусть M(x,y) - любая точка этой
окружности, а t - угол между
радиусом-вектором
MO и осью Ox,
отсчитываемой против часовой
стрелки. Тогда x=rcos t, y=rsin t
(2.2).
Эти уравнения представляют собой параметрические уравнения нашей
окружности. Чтобы точка M(x,y) один раз обошла окружность, t должно
изменяться в пределах:
π
2 t 〈≤0 . Для исключения параметра t из уравнения (2.2),
нужно возвести в квадрат и сложить уравнения (2.2); получим
.
222
ryx =+
1.4.2. Уравнение линии в полярных координатах
Введем на плоскости полярные координаты. выберем на плоскости точку O
(полюс) и выходящий из нее луч Ox; укажем единицу масштаба.
y
M
ρ
ϕ
0 x
Полярными координатами точки M называются два числа: ρ (полярный
радиус) равное расстоянию точки M от полюса O и ϕ (полярный угол) - угол, на
который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом
OM. Точку M обозначают символом
(
)
ϕ
ρ
,
Μ
и обычно считают, что
π
ϕ
ρ
2<0 ,0 ≤+∞<≤ .
Если начало декартовой прямоугольной системы находится в полюсе, а ось
абсцисс совпадает с полярной осью, то очевидна связь между полярными
координатами точки
()
ϕ
ρ
,Μ и ее декартовыми координатами :
()
y,xM
ϕ
ρ
ϕ
ρ
siny ,cosx
=
= (3.1)
Возводя эти уравнения в квадрат и складывая их, получим
22
yx +=
ρ
.
Разделив одно на другое, получим, что
x
y
tg =
ϕ
, а также используя знаки x и y,
определим четверть, в которой находится точка M. Т.е., зная декартовы
координаты точки x и y можно найти ее полярные координаты.
Если Ф(x,y)=0 представляет собой уравнение линии L в декартовой
прямоугольной системе координат Oxy, то достаточно подставить на место x и y
их выражения в полярных координатах (3.1): получим
()
0,
1
=
Φ
ϕ
ρ
, где
использовали обозначение
()
(
)
ϕ
ρ
ϕ
ρ
ϕ
ρ
sin ,cos,
1
Φ
=
Φ .
1.4.3. Пересечение двух линий
Задача о нахождении точек пересечения двух линий , заданных
уравнениями
21
L è L
() ()
0y,x è 0y,x
21
=
Φ=Φ , состоит в нахождении координат точек,
удовлетворяющих каждому из этих уравнений.
Т.е. нужно решить систему уравнений
()
()
=Φ
=Φ
0y,x
0y,x
2
1
Если эта система не имеет решений, то линии
не пересекаются.
21
L è L
Пример. Найти точки пересечения окружностей
.
()
02y1-x è 01yx
2
2
22
=−+=−+
Решаем систему уравнений
()
=−+−
=−+
02y1x
01yx
2
2
22
Вычитая из первого уравнения второе, получим
()
0.= x0,=2x èëè 011xx
2
2
=+−−
Отсюда найдем, что
1y
±
=
. Мы получили две точки пересечения
.
() (
1,0M è 1,0M
21
−
)
1.4.4. Уравнение поверхности и уравнение линии в пространстве
Пусть нам заданы декартова прямоугольная система координат Oxyz и
некоторая поверхность S.
Определение 1. Уравнение
Ф(x,y,z)=0
называется уравнением поверхности S (относительно заданной системы
координат), если этому уравнению удовлетворяют координаты x, y, z любой
точки, лежащей на поверхности S, и не удовлетворяют координаты x, y, z ни
одной точки, не лежащей на поверхности S.
Пример. Уравнение сферы радиуса R>0 с центром в точке
в
декартовой прямоугольной системе координат Oxyz имеет вид
()
0000
z,y,xΜ
()
(
)
(
)
2
2
0
2
0
2
0
Rzzyyxx =−+−+− .
Действительно, точка M(x,y,z) лежит на указанной сфере тогда и только
тогда, когда квадрат расстояния между точками M(x,y,z) и
()
0000
,, zyx
Μ
(
)
(
)
(
)
2
R ðàâåí
2
0
zz
2
0
yy
2
0
xx −+−+−
.
Определение 2. Линия в пространстве есть геометрическое место точек, лежащих
одновременно на двух поверхностях.
Таким образом линия в пространстве рассматривается как линия
пересечения двух поверхностей.
Если
() ()
0z,y,x è 0=z,y,x
21
=
ΦΦ - уравнения двух поверхностей,
пересечением которых является данная линия L, то два уравнения
()
()
=Φ
=Φ
0z,y,x
0z,y,x
2
1
совместно определяют линию L.
Как и в случае плоской линии (п.2) можно линию в пространстве
представить параметрически, задав координаты x, y, z любой точки данной
линии как непрерывные функции некоторого параметра t :
() () ()
tz,ty,tx
χ
ψ
ϕ
=== ,

определенные в некотором промежутке изменения параметра
{
.
}
t
Для отыскания точек пересечения поверхностей и линий следует решить
совместно уравнения, определяющие указанные линии и поверхности.
1.5. Различные виды уравнений прямой на плоскости
1.5.1. Общее уравнение прямой
Уравнение
Ax+By+C=0 (6.1)
с произвольными коэффициентами A, B и C такими, что A и B не равны
одновременно нулю, называется общим уравнением прямой L.
Уравнение (6.1) имеет хотя бы одно решение
, т.е. существует точка
, координаты которой удовлетворяют уравнению (6.1):
00
y ,x
(
000
y,xΜ
)
0CByAx
00
=
+
+
(6.2)
Вычитая из уравнения (6.1) тождество (6.2), получаем уравнение
()
(
)
0yyBxxA
00
=
−
+
− , (6.3)
эквивалентное уравнению (6.1).
Если точка M(x,y) лежит на прямой L, то ее координаты удовлетворяют
уравнению (6.3), векторы
{
}
B,An
=
, перпендикулярный к прямой L и
перпендикулярны и их скалярное произведение
{
000
yy,xx −−=ΜΜ
}
(
)
(
)
00
yyBxxA
−
+
−
равно нулю. Если же точка M(x,y) не лежит на прямой L , то ее координаты не
удовлетворяют уравнению (6.3).
Итак, уравнение (6.3) определяет прямую L, проходящую через точку
(
)
00
y,xΜ и перпендикулярную вектору
{
}
B,An
=
. Этот вектор будем называть
нормальным вектором прямой (6.1).
Замечание. Если два уравнения
0CyBxA è 0CByAx
111
=+
+
=
+
+
определяют
одну и ту же прямую, то существует такое вещественное число t, что справедливы
равенства
CtC ,BtB ,AtA
111
=
=
= .
1.5.2. Уравнение прямой с угловым коэффициентом
y
n
α
0 x
Пусть прямая не параллельна оси
Ox, тогда в уравнении (6.1)
коэффициент
0
≠
Β
. Углом
наклона этой прямой к оси Ox
назовем угол α>0, образованный
прямой с положительным
направлением оси Ox.

Если прямая параллельна оси Ox, то угол наклона α будем считать равным
нулю.
Угловым коэффициентом прямой назовем тангенс угла наклона этой
прямой к оси Ox, k=tgα.
Для прямой, параллельной оси Ox, угловой коэффициент равен 0, а для
прямой, перпендикулярной оси Ox, угловой коэффициент не существует
(
)
∞
=
κ
.
Из уравнения (6.3) и того, что
{
}
B,An
=
- нормальный вектор прямой следует,
что
B
A
tg −==
κα
.
Отсюда получим уравнение прямой с угловым коэффициентом в виде
(
00
xxyy −=−
)
κ
. Если обозначить b
00
kxy
−
=
, то последнее уравнение примет вид
bkxy
+
=
(6.4)
Это уравнение и называется уравнением прямой с угловым коэффициентом.
Здесь k- угловой коэффициент данной прямой, а b - отрезок, отсекаемый данной
прямой на оси Oy, начиная от начала координат (при x=0, y=0).
1.5.3. Уравнение прямой в отрезках
Рассмотрим полное (все коэффициенты A, B и C отличны от нуля)
уравнение прямой
Ax+By+C=0.
Его можно записать в виде (т.к.
0C,0B,0A
≠
≠
≠
)
1
B
C
y
A
C
x
=
−
+
−
и затем положить
A
C
b ,
A
C
a −=−=
. Получим 1
b
y
a
x
=+
.
Последнее уравнение называется уравнением прямой “в отрезках”. Числа a
и b равны соответственно величинам отрезков, отсекаемых прямой на осях Ox и
Oy соответственно.
1.5.4. Каноническое уравнение прямой
Любой ненулевой вектор, параллельный данной прямой, назовем
направляющим вектором этой прямой.
Найдем уравнение прямой, проходящей через данную точку
(
)
000
y,xΜ и
имеющей заданный направляющий вектор
{
}
m,lq
=
.
Точка M(x,y) лежит на указанной прямой тогда и только тогда, когда векторы
{}{}
ml,=q è yy,xx
000
−−=ΜΜ коллинеарны, т.е. когда их координаты
пропорциональны
m
yy
l
xx
00
−
=
−
(6.5)
Это уравнение обычно называют каноническим уравнением прямой.
В уравнении (6.5) одно из чисел l или m может равняться нулю, т.к. это есть
координаты вектора. например, уравнение оси Ox запишется так
0
0y
1
0x
−
=
−
.

1.5.5. Параметрические уравнения прямой
Примем за параметр t величину, стоящую в правой и левой частях
соотношения (6.5),
∞<<
∞
−
t .
Получим x mtyy ,ltx
00
=−
=
− или
+=
+=
mtyy
ltxx
0
0
Это и есть искомые параметрические уравнения прямой.
1.5.6. Угол между двумя прямыми. Условия параллельности и
перпендикулярности двух прямых
1). Пусть прямые L
1
и L
2
заданы общими уравнениями
0CyBxA è 0CyBxA
22222
=
+
+
=
++ .
Задача об определении угла между прямыми сводится к определению угла
между нормальными векторами
{
}
{
}
222111
B,An è B,An
=
=
этих прямых:
2
2
2
2
2
1
2
1
2121
BABA
BBAA
cos
+⋅+
+
=
α
(6.6)
Условие параллельности прямых L
1
и L
2
эквивалентно коллинеарности их
нормальных векторов
21
n è n :
2
1
2
1
B
B
A
A
=
.
Условие перпендикулярности прямых L
1
и L
2
получаем из формулы (6.6)
при cosϕ=0:
0BBAA
2121
=
+
.
2). Если прямые L
1
и L
2
заданы каноническими уравнениями
2
2
2
2
1
1
1
1
m
yy
l
xx
è
m
yy
l
xx
−
=
−
−
=
−
,
то рассматривая их направляющие векторы
{
} {
222111
m,lq è m,lq =
}
=
, аналогично
случаю 1). имеем:
2
2
2
2
2
1
2
1
2121
mlml
mmll
cos
++
+
=
ϕ
(6.7)
Условие параллельности прямых L
1
и L
2
:
2
1
2
1
m
m
l
l
=
.
Условие перпендикулярности прямых L
1
и L
2
:
0mmll
2121
=
+
3). Пусть прямые L
1
и L
2
заданы уравнениями с угловым коэффициентом
2211
bxk=y è bxky
+
+= .
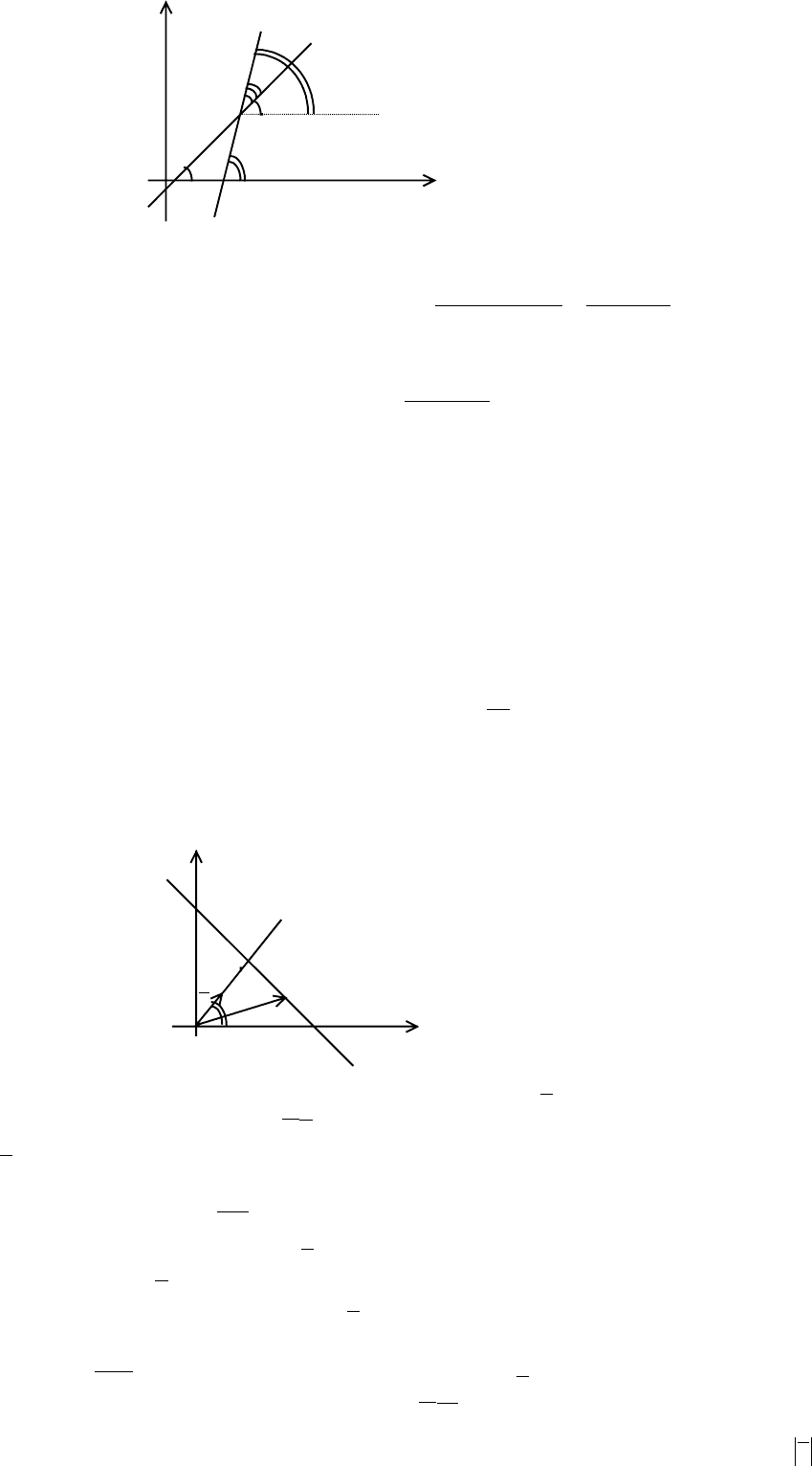
y
L
2
L
1
ϕ
α
1
α
2
α
1
α
2
0 x
Здесь
21
è
α
α
- углы наклона
прямых L
1
и L
2
к оси Ox, а ϕ-
один из углов между этими
прямыми. Из рисунка видно,
что
12
α
α
ϕ
−
=
.
Отсюда
()
21
12
21
12
12
kk1
kk
tgtg1
tgtg
tgtg
⋅+
−
=
⋅+
−
=−=
αα
α
α
ααϕ
.
Т.е. угол между прямыми L
1
и L
2
определяется по формуле:
21
12
kk1
kk
tg
⋅+
−
=
ϕ
(6.8)
Если в этой формуле поменять местами k
1
и k
2
, то формула определит нам
угол между прямыми, смежный к прежнему углу. Т.к. эти два угла в сумме равны
π и их тангенсы отличаются только знаком.
Прямые параллельны, если tgϕ=0, т.е. k
1
=k
2
.
Условие перпендикулярности прямых L
1
и L
2
получим из формулы (6.8),
т.к. tgϕ не существует при
01kk
21
=
+ .
Условие перпендикулярности прямых L
1
и L
2
запишем в виде:
1
2
k
1
k −=
.
1.5.7. Нормированное уравнение прямой. Отклонение точки от прямой
y
L
n
P
n
θ M
0 x
Рассмотрим произвольную
прямую L. Через начало
координат O проведем прямую
n, перпендикулярную L, и
обозначим через P точку
пересечения этих прямых.
На прямой n возьмем единичный вектор n , направление которого совпадает
с направлением отрезка
PO (если точки O и P совпадают, то направление вектора
n выбираем произвольно).
Выразим уравнение прямой L через два параметра:
1) длину p отрезка
PO и
2) угол θ между вектором
n и осью Ox.
Вектор
n - единичный, следовательно его можно записать в виде
{
}
θ
θ
sin , cosn
=
(6.9)
Точка M(x,y) лежит на прямой L тогда и только тогда, когда проекция
вектора
MO на ось, определяемую вектором n , равна p:
pMOðï
n
= . (6.10)
В силу определения 2 скалярного произведения, учитывая, что
1n = имеем:

(
)
MOnMOðï
n
⋅= . (6.11)
Учитывая, что
{
y,xMO =
}
и равенство (6.9), получим
(
)
θθ
sinycosxMOn +=⋅ (6.12)
Из соотношений (6.9), (6.10) и (6.11) получаем, что точка M(x,y) лежит на
прямой L тогда и только тогда, когда ее координаты удовлетворяют уравнению
0psinycosx
=
−
+
θ
θ
(6.13)
Это уравнение называется нормированным уравнением прямой.
Пусть число d обозначает расстояние от точки M до прямой L.
Определение. Отклонением δ точки M от прямой L называется число +d в случае,
когда точка M и начало координат O лежат по разные стороны от прямой L, и
число -d в случае, когда точки M и О лежат по одну сторону от прямой L. Если же
начало координат О лежит на прямой L, положим отклонение равным +d в случае,
когда точка М лежит по ту сторону от прямой L, куда направлен вектор
n , и
равным -d в противоположном случае.
Теорема. Геометрический смысл левой части уравнения (6.13) состоит в том, что
левая часть этого уравнения равна отклонению точки M(x,y) от прямой L,
определяемой уравнением (6.13).
Доказательство.
y
L Q
P
M
n
0 x
Спроектируем точку М на ось,
определяемую вектором
n ,
обозначим эту проекцию Q.
Отклонение δ точки М от прямой L
равно PQ, где PQ обозначает
величину направленного отрезка
QP оси, определяемой вектором n .
Из рисунка видно, что
pOQOPOQPQ
−
=
−
==
δ
, (6.14)
но
MOðïOQ
n
= , а в силу (6.11) и (6.12) получаем
θ
θ
sinycosxOQ
+
=
.
Из последнего равенства и (6.14) имеем
psinycosx
00
−
+
=
θ
θ
δ
.
Отсюда получаем возможность находить расстояние от точки
(
)
000
y,xΜ до
прямой L:
psinycosxd
00
−+=
θθ
.
1.5.8. Приведение общего уравнения прямой к нормированному виду
Пусть нам дано общее уравнение прямой Ax+By+C=0. Требуется привести
его к виду (6.13).
Т.к. эти уравнения должны определять одну и ту же прямую, то найдется
число t такое, что
.ptC,sintB,costA
−
=
=
=
θ
θ
Возводя в квадрат два первых равенства и складывая их, получим
()
22
222
BA
1
= tèëè 1BAt
+
±=+
.
Т.к. по условию задачи p≥0, то из равенства tC=-p заключаем, что знак t
противоположен знаку С.

Таким образом, для приведения общего уравнения прямой 0CByAx
=
+
+ к
нормированному виду следует умножить его на нормирующий множитель
22
BA
1
t
+
±=
, знак которого противоположен знаку С.
Отсюда очевидна формула для вычисления расстояния d от точки
до прямой Ax :
(
000
y,xΜ
)
0CBy =++
22
00
BA
CByAx
d
+
++
=
.
2. Кривые второго порядка
Будем рассматривать линии, уравнения которых в декартовой системе координат
являются алгебраическими уравнениями второй степени, то есть будем рассматривать
алгебраические кривые второго порядка. Будут рассмотрены три вида линий второго порядка:
эллипсы, гиперболы и параболы. Основной целью является ознакомление с важнейшими
геометрическими свойствами указанных линий.
2.1. Эллипс
2.1.1. Определение эллипса и вывод его канонического уравнения
Эллипсом называется геометрическое место точек на плоскости, для которых сумма
расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная
величина.
Y
M(x,y)
r
2
r
1
X
F
2
(-c;0) 0 F
1
(c;0)
Рис.1
Для вывода уравнения
эллипса выберем систему координат
XOY так, чтобы фокусы эллипса F
1
и F
2
лежали на оси абсцисс, а
начало координат делило бы
расстояние между фокусами
пополам (Рис.1). Обозначим
F
1
F
2
=2c. Тогда координаты фокуса
F
1
будут (с;0), а координаты фокуса
F
2
будут (-с;0).
Возьмем произвольную точку М(x,y), лежащую на эллипсе. Соединим точку М с
фокусами F
1
F
2
. Длины отрезков MF
1
и MF
2
обозначим соответственно через r
1
r
2
: МF
1
=r
1
;
MF
2
=r
2
. Числа r
1
и r
2
называются фокальными радиусами точки М эллипса. Учитывая, что
сумма r
1
и r
2
есть величина постоянная (это следует из определения эллипса) обозначим:
r
1
+r
2
=2a, следует 2а>2c или a>c. В противном случае либо не существует точек,
удовлетворяющих поставленным требованиям, либо совокупность этих точек сводится к
отрезку F
1
F
2
.
На основании определения эллипса как геометрического места точек, можно утверждать,
что для всех точек эллипса, и только для них, должно выполняться равенство:
r
1
+r
2
=2a (1)
Определим r
1
и r
2
по формулам расстояния между двумя точками:
()
2
2
1
ycxr +−= (2)
()
2
2
2
yc+xr += (3)
Поставляя найденные значения r
1
и r
2
в уравнение (1), получим:
() ()
2aycxycx
2
2
2
2
=++++− (4)
Уравнение (4) является
уравнением эллипса. Однако полученная форма уравнения
является неудобной для пользования, поэтому обычно уравнение эллипса дается в ином виде.
