Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


Если ({x
n
}∈Б)⇒( {x
n
}∉m). Действительно,
{}()()( ){}()
[
)
.:0
00
AxnnxxNnAçx
nnn
def
n
>⇒≥∈∀∈∃>∀≡∈
Следовательно, найдется по крайней мере один такой элемент x
n
, что
| x
n
|>А. Обратное, вообще говоря, неверно. Неограниченная последовательность
{1, - n} не является бесконечно большой, т.к. при А>1 для всех элементов x
n
с
нечетными номерами неравенство
| x
n
|>А не имеет места.
Определение 5. Последовательность
{x
n
} называется бесконечно малой
последовательностью (
{x
n
}∈δ), если для любого положительного числа ε (сколь
бы малым мы его ни взяли) можно указать номер n
0
такой, что при n ≥ n
0
все
элементы x
n
этой последовательности удовлетворяли неравенству | x
n
|< ε
{}()()(){}()
[]
εεδ
<⇒≥∈∀∈∃>∀≡∈
nnn
def
n
xnnxxNnx
00
:0 .
Так как номер n
0
, вообще говоря, зависит от ε, то часто пишут n
0
=n
0
(ε)
-
ε
0
ε
В незаштрихованной на рисунке области останется лишь конечное число
элементов последовательности
{x
n
}.
4.2.3. Основные теоремы о бесконечно малых последовательностях
Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно
малая последовательность
{}
{
}()
{
}
(
)
δ
β
α
δ
β
δ
α
∈
±
⇒
∈
∧
∈
nnnn
.
Следствие. Алгебраическая сумма любого конечного числа бесконечно малых
последовательностей есть бесконечно малая последовательность.
Теорема 2. Бесконечно малая последовательность ограниченна.
{}(){}()
.m
nn
∈⇒∈
α
δ
α
Теорема 3. Произведение ограниченной последовательности на бесконечно
малую последовательность является бесконечно малой последовательностью
{} {}(){()
.
}
δ
α
δ
α
∈⇒∈∧∈
nnnn
xmx
Следствие. Произведение любого конечного числа бесконечно малых
последовательностей является бесконечно малой последовательностью.
Замечание 1. Частное двух бесконечно малых последовательностей может быть
последовательностью любого типа и даже может не иметь смысла:
1. Если, например,
α
n
= 1/n и β
n
= 1/n, то все элементы последовательности {α
n
/ β
n
} равны 1.
2. Если
α
n
= 1/n, β
n
= 1/n
2
, то {α
n
/ β
n
}∈Б.
3. Если
α
n
= 1/n
2
, β
n
= 1/n, то {α
n
/ β
n
}∈δ.
При определении частного двух последовательностей предполагается, что у
последовательности
{β
n
} все элементы β
n
отличны от нуля, начиная с некоторого
номера.
Теорема 4. Если все элементы бесконечно малой последовательности
{α
n
} равны
одному и тому же числу с, то с=0
{} (
0=⇒
≡=∀∧∈ ccconst
def
nn
αδα
)
.

Теорема 5. Если последовательность {x } является бесконечно большой, то
начиная с некоторого номера n определена последовательность
{1/x }, которая
является бесконечно малой. Если все элементы бесконечно малой
последовательности {α } не равны 0, то последовательность {1/α } является
бесконечно большой.
n
n
n n
{}()()
(
)
{
}
[
]
{}(){}()
./10
/1:
00
Á
xnnNnNnÁx
nnn
nn
∈⇒≠∀∧∈
∈
⇒≥
∈
∀
∈
∃⇒∈
ααδα
δ
4.2.4. Сходящиеся последовательности. Основные определения
Определение 1. Последовательность
{x
n
} называется сходящейся ({x
n
}∈с), если
существует такое действительное число а, что последовательность
{x
n
- а}
является бесконечно малой последовательностью
{}()(){}
[]
.:
δ
∈−∈∃≡∈ axRacx
n
def
n
Замечание. Исходя из этого определения следует, что всякая бесконечно малая
последовательность является сходящейся и имеет своим пределом 0.
Определение 2.
{}()()()( ){}()
[]
.:0
00
εε
<−⇒≥∈∀∈∃>∀∈∃≡∈ axnnxxNnRacx
nnn
def
n
Очевидно, что неравенство
| x
n
- а|<ε эквивалентно неравенствам
-
ε< x
n
-а < ε или а-ε< x
n
< а+ε , которое означает, что некоторый элемент x
n
последовательности { x
n
} принадлежит ε, окрестности числа а, поэтому
определение сходящейся последовательности можно дать следующим образом:
a −ε
a
x
n
a +ε
Определение 3. Последовательность
{x
n
} называется сходящейся, если
существует действительное число а такое, что в любой
ε - окрестности числа а
находятся все элементы последовательности
{x
n
} начиная с некоторого номера.
Число а, фигурирующее в определениях, называется пределом
последовательности
{x
n
}.
Символическая запись существования предела последовательности
{x
n
},
равного а, записывается так: ax
n
n
=
∞→
lim , или {x
n
}→а при n→∞ .
Бесконечно большие последовательности иногда называются
последовательностями, сходящимися к бесконечности, поэтому если
{x
n
}∈Б, то
символически это записывается следующим образом:
lim
= ∞, или {x
∞→n
n
x
n
}→ ∞ при
n
→ ∞.
Если элементы бесконечно большой последовательности начиная с
некоторого номера имеют определенный знак, то говорят, что
{x } сходится к
бесконечности определенного знака
= +∞
n
∞→n
n
xlim
или
lim
= - ∞.
∞→n
n
x
Замечание 1. Из определения 1 сходящейся последовательности вытекает, что
последовательность
{x
n
- а}∈δ. Обозначая элементы этой последовательности
через
α
n
, α
n
= x
n
-а, мы получим, что любой элемент x
n
сходящейся
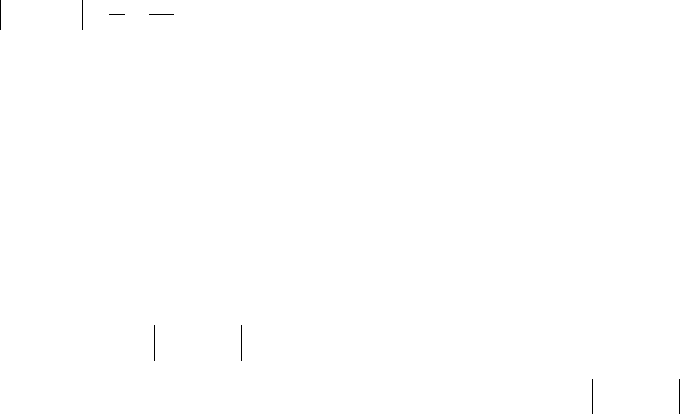
последовательности {x
n
}, имеющей пределом число а, может быть представлен в
виде x
n
=a+α
n
, где α
n -
элемент бесконечно малой последовательности.
Замечание2.
Из определения предела последовательности вытекает, что конечное
число элементов не влияет на сходимость этой последовательности и на величину
ее предела.
Пример. Покажем, что последовательность
{1+ (-1)
n
/n}сходится. Пределом этой
последовательности является число 1. Для доказательства достаточно показать,
что последовательность
{x
n
- а}= {(-1)
n
/n}∈δ. В самом деле, если n ≥ n
0
, то
()
,
11
/1
0
nn
nn <=− поэтому по данному ε>0 следует выбрать номер n
0
такой, чтобы
выполнялось условие 1/n
0
<ε, т.е. n
0
=[1/ε]+1, где [x]- целая часть числа x - т.е.
наибольшее целое число, не превышающее x.
(Например,
[6,187]=6; [-5,87]=-6 ).
В качестве n
0
можно взять и любой номер [1/ε]+к, где к>1.
Определение 4.
Последовательность {x
n
} называется фундаментальной ({x
n
}∈Φ),
если для любого положительного числа
ε найдется номер n
0
такой, что для всех
номеров n , удовлетворяющих условию n
≥ n
0
, и для всех натуральных чисел
р(р=1, 2, . . . ), все элементы x
n
этой последовательности удовлетворяют
неравенству
ε
<−
+ npn
xx
{}()()()(){}()
[
]
εε
<−⇒≥∈∀Ν∈∀Ν∈∃>∀≡Φ∈
+ npnnn
def
n
xxnnxxpnx
00
:0 Сформулируем
без доказательства Критерий Коши о необходимом и достаточном условии
сходимости последовательности.
Теорема. Для того, чтобы последовательность
{x
n
} была сходящейся, необходимо
и достаточно, чтобы она былы фундаментальной.
{
}
(
)
{
}
(
)
.
Φ
∈
⇔
∈
nn
xcx
4.2.5. Основные свойства сходящихся последовательностей
Теорема 1. Сходящаяся последовательность имеет только один предел
{}() (
.limlim
=⇒
=∧
=⇒∈
∞→∞→
baxbxacx
n
n
n
nn
)
Теорема 2. Сходящаяся последовательность ограничена
{}(){}()
.mxcx
nn
∈
⇒∈
Замечание. Обратная теорема не имеет места, ибо ограниченная
последовательность, вообще говоря, может и не быть сходящейся. Так, например,
{x
n
}={1+(-1)
n
}=0, 2, 0, 2, 0, 2, . . . ограниченна, но не является сходящейся.
Действительно, если бы
{x
n
}∈с и
∞→
=
n
n
axlim
, то {x
n
-a}∈δ и {x
n +1
- а}∈δ, тогда и {(x
n
-a)- (x
n +1
- а)} ∈δ (теорема 1,2,3).
Но
{(x
n
-a)- (x
n +1
- а)}={x
n
- x
n +1
} не является бесконечно малой, т.к.
|x
n
- x
n +1
| = 2 для ∀n∈N.
4.2.6. Арифметические свойства сходящихся последовательностей
Теорема 1. Если последовательности
{x
n
} и {y
n
} сходятся, то сумма (разность),
произведение и частное этих последовательностей (частное при условии, что

предел последовательности {y
n
}≠0) есть сходящиеся последовательности,
пределы которых соответственно равны: сумме (разности), произведению и
частному пределов этих последовательностей
()
≠∧==±=±⇒
⇒
=∧
=
∞→∞→∞→
∞→∞→
0lim;lim;lim
limlim
b
b
a
y
x
abyxbayx
byax
n
n
n
nn
n
nn
n
n
n
n
n
4.2.7. Монотонные последовательности
Определение 1. Последовательность
{x
n
} называется невозрастающей
(неубывающей) последовательностью, если каждый последующий член этой
последовательности не больше (не меньше) предыдущего, т.е. если для
∀n∈N
справедливо неравенство x
n
≥ x
n +1
(x
n
≤ x
n +1
). Такие последовательности
называются монотонными последовательностями.
Определение 2.
Если для всех номеров n элементы последовательности {x
n
}
удовлетворяют неравенству x
n
> x
n +1
(x
n
< x
n +1
), то такая последовательность
называется убывающей (возрастающей). Убывающие и возрастающие
последовательности называются строго монотонными.
Замечание. Отметим, что неубывающие и невозрастающие последовательности
ограничены сверху и снизу соответственно своими первыми элементами.
Поэтому неубывающая (невозрастающая) последовательность будет ограничена с
двух сторон, если она ограничена сверху (снизу).
Введем следующие обозначения:
↑ {x
n
} - невозрастающая последовательность {x
n
},
↓ {x
n
} - неубывающая последовательность {x
n
},
↑ {x
n
} - возрастающая последовательность{x
n
},
↓ {x
n
} - убывающая последовательность {x
n
}.
Пример 1. Последовательность
{n,n}=1,1,2,2, . . .n,n, . . . неубывающая
монотонная. Снизу она ограничена первым элементом - “1”, а сверху не
ограничена.
Пример 2. Последовательность
,...
1
,...,
4
3
,
3
2
,
2
1
1 +
=
+
n
n
n
n
возрастающая. Снизу эта
последовательность ограничена своим первым элементом
2
1
, а сверху , например,
своим пределом- единицей, т.е. эта последовательность ограничена.
Теперь докажем основную теорему о сходимости монотонной
последовательности.
Теорема. Если неубывающая (невозрастающая) последовательность ограничена
сверху (снизу), то она сходится.
[ ({x
n
}∈m )∧(↓ {x
n
})]⇒{x
n
}∈ c,
[ ({x
n
}∈m )∧(↑ {x
n
})]⇒{x
n
}∈ c.
В силу замечания, сформулированного выше, неубывающие
(невозрастающие), ограниченные сверху (снизу) последовательности являются
ограниченными с обеих сторон. Поэтому последнюю теорему можно
сформулировать так:

.
{}
{}
{}
{}
cx
x
x
mx
n
n
n
n
∈⇒
↓
↑
∧∈
Замечание 1. Условие ограниченности монотонной последовательности есть
необходимое и достаточное условие ее сходимости.
В самом деле, если монотонная последовательность ограничена, то в силу
доказанной теоремы она сходится.
Если же монотонная последовательность (да и, вообще, любая
последовательность) сходится, то она ограничена (см. теорему 2).
Замечание 2. Если последовательность сходится, то она может и не быть
монотонной. Так, последовательность
{
}
{
}
nx
n
n
/)1(−= сходится и имеет пределом
“0”. Однако эта последовательность не является монотонной, т.к. знаки элементов
этой последовательности чередуются.
4.2.8. Число е
Рассмотрим пример последовательности, для нахождения предела которой
будет использована вышеуказанная теорема (п. 2.7.) о пределе монотонной
последовательности.
Пусть дана последовательность
{
}
(
)
{
}
n
n
nx 11+= , т.е. каждый элемент этой
последовательности
(
n
n
nx 11+=
)
. Покажем, что эта последовательность возрастает
и ограничена сверху.
Используя формулу бинома Ньютона
()
[] []
,
!
)1()...1(
...
!
)1()...1(
...
!3
)2)(1(
!2
)1(
1
33221
nnmmn
nnnn
n
b
n
nnnn
nabba
m
mnnn
ba
nnn
ba
nn
bnaaba
−−−
+++
−−−
+
++
−
−
+
−
++=+
−−
−−−
получим
[]
n
n
nn
nnnnn
n
nnn
n
nn
n
nx
1
!
)1()...2)(1(
...
1
!3
)2)(1(1
!2
)1(1
1
32
−−−−
+
++
−
−
+
−
++=
или
[]
,
...
)1()...2)(1(
!
1
...
)2)(1(
!3
1)1(
!2
1
2
nnnn
nnnnn
nnnn
nnn
nn
nn
x
n
⋅⋅⋅
−−
−
−
++
⋅⋅
−
−
+
⋅
−
++=
или
−
−
−
−++
−
−+
−+=
n
n
nnnnnn
x
n
1
1...
2
1
1
1
!
1
...
2
1
1
1
!3
11
1
!2
1
2
. (1)
Аналогично этому
+
−
+
−
+
+
+
+
−
−
+
−++
+
−
+
−+
+
−+=
+
1
1...
1
1
1
)!1(
1
1
1
1...
1
1
1
!
1
...
1
2
1
1
1
1
!3
1
1
1
1
!2
1
2
1
n
n
nn
n
n
nnnnn
x
n
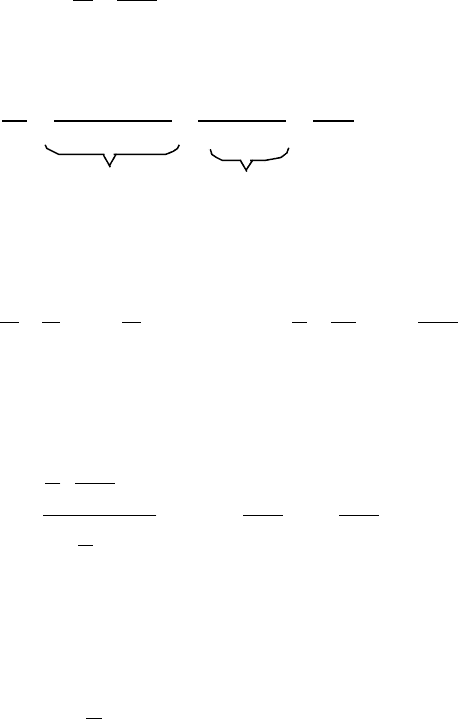
Очевидно, что 1)
+
−<
−
1
11
n
k
n
k
для любого nkk
≤
≤
1 : ;
2) все члены последовательности
{
}
n
x строго положительны;
3) x
n+1
по сравнению с х
n
содержит лишний положительный член.
Поэтому х
n
<x
n+1
и
{
- возрастающая последовательность. Покажем теперь
ограниченность сверху этой последовательности.
}
n
x
Используем неравенство
2 ,
2
1
!
1
1
≥<
−
k
k
k
. (2)
Действительно,
11
1234
1
122 2
1
2
1
kk
k
!......
=
⋅⋅⋅
≤
⋅⋅
=
−
.
k k-1
Учитывая, что каждое выражение в круглых скобках формулы (1) строго меньше
1, и заменяя его поэтому единицей, получим, что
.
2
1
...
2
1
2
1
2
!
1
...
!3
1
!2
1
2
12 −
++++<++++<
n
nn
xèëè
n
x
Суммируя n-1 член убывающей геометрической прогрессии со
знаменателем 1/2, получим
.3
2
1
3
2
1
12
1
2
1
1
2
1
2
1
2
11
1
<−=−+=
−
−
+<
−−
−
nn
n
n
x
Итак, последовательность
возрастает и ограничена сверху.
{}
n
x
По доказанной теореме (п. 2.7.) эта последовательность имеет предел, который
называют числом е.
По определению
n
n
n
e
+=
∞→
1
1lim
.
4.2.9. Предельный переход в неравенствах
Покажем, что неравенства, которым удовлетворяют элементы сходящихся
последовательностей, в пределе переходят в соответствующие неравенства для
пределов этих последовательностей.
Теорема 1. Если элементы сходящейся последовательности
{
}
n
x начиная с
некоторого номера удовлетворяют неравенству
(bx
n
≥ bx
n
≤
), то и предел а этой
последовательности удовлетворяет неравенству
(ba ≥ ba
≤
)
{}()()()
)(
)(
)(
)(
:
00
ba
ba
bx
bx
Nnnnax
n
n
n
≤
≥
⇒
≤
≥
∈∧≥∀∧→
.
Замечание. Если элементы сходящейся последовательности
{
удовлетворяют
строгому неравенству x
}
n
x
n
>b, то предел а этой последовательности может все же
оказаться равным b.

Так, члены последовательности
{
}
{
}
nx
n
1
=
строго положительны )01 >n( , а
предел этой последовательности равен нулю.
Следствие 1.
{}(){}()
[]
()()
)(
)(
)(
)(
:
00
ba
ba
yx
yx
Nnnnbyax
nn
nn
nn
≥
≤
⇒
≥
≤
∈∧≥∀∧→∨→
.
Если элементы x
n
и y
n
сходящихся последовательностей и
{
начиная
с некоторого номера удовлетворяют неравенству
{}
n
x
}
n
y
nn
yx
≤
( ), то их пределы
удовлетворяют такому же неравенству
lim
n
)
n
y
n
yx ≥
lim
n
n
∞→
≥lim(
n
n
y
∞→
lim
n
n
n
xx
∞→∞→
≤
.
Следствие 2. Если все элементы сходящейся последовательности
{
начиная с
некоторого номера находятся на сегменте [a,b], то и ее предел С также находится
на этом сегменте.
}
n
x
{}()()
(
)
(
)
[]
{}
)(
0
bcabxaNnnncx
nn
≤
≤
⇒
≤
≤
∈
∧
≥∀∧→ .
Теорема 2. Пусть последовательности
{
}
n
x и
{
}
n
z cходятся и имеют общий предел
а. Пусть начиная с некоторого номера элементы последовательности
{}
удовлетворяют неравенствам
n
y
nnn
zyx
≤
≤
. Тогда последовательность
{
сходится
и имеет предел а.
}
n
y
4.2.10. Подпоследовательности числовых последовательностей
Пусть x
1
, x
2
,.., x
k
,... некоторая числовая последовательность.
Рассмотрим произвольную возрастающую последовательность целых
положительных чисел n
1
, n
2
,.., n
k
,... и выберем из последовательности
{}
элементы с номерами n
k
x
1
, n
2
,.., n
k
,... . Расположим эти элементы в таком же
порядке, как и числа
. Полученную таким образом числовую
последовательность будем называть подпоследовательностью
последовательности
,...,...,,:
21 k
nnnk
xxxn
{
}
k
x . В частности, сама последовательность может
рассматриваться как подпоследовательность (в этом случае n
k
= k).
Замечание. Очевидно, что для любого номера k справедливо неравенство
n .
Это видно из следующего примера:
k
k
≥
{}
,...,...,,,
321 kk
xxxxx =
{
}
,...20,17,15,10,9,8,3
=
k
n
Если k = 5, то n
k
= 15 и . kn
k
≥
Свойство 1. Если последовательность
{
}
k
x сходится и имеет своим пределом
число а, то и любая подпоследовательность этой последовательности сходится и
имеет пределом число а
{}()
{
}
{
}
(
)
axxax
knk
k
→
∈
∀
⇒→ .
Свойство 2. Если все подпоследовательности данной последовательности
сходятся, то пределы всех этих подпоследовательностей равны одному и тому
же числу а; в частности, к этому же числу сходится и последовательность
{}
k
x
{
}
k
x
{
}
{}
(
)
{
}
(
)
{
}
(
)
{
}
(
)
[
]
axaxcxxx
knnkn
kkk
→
∧
→∀⇒∈∀∧∈∀ .
Свойство 3. Каждая подпоследовательность бесконечно большой
последовательности также будет бесконечно большой
{}()
{
}
(
)
.ÁxÁx
k
nk
∈∀⇒∈
Лемма 1. Из каждой сходящейся последовательности можно выделить
монотонную сходящуюся последовательность.
Замечание. Из каждой бесконечно большой последовательности можно выделить
монотонную бесконечно большую последовательность.
4.2.11. Предельные точки последовательности
Определение 1. Точка x бесконечной прямой называется предельной точкой
последовательности {x
n
}, если в любой ε - окрестности этой точки имеется
бесконечно много элементов последовательности {x
n
}.
Лемма 1. Если x- предельная точка последовательности {x
k
}, то из этой
последовательности можно выделить подпоследовательность {x
nk
}, сходящуюся к
числу x.
Замечание. Справедливо и обратное утверждение. Если из последовательности
{x
k
} можно выделить подпоследовательность, сходящуюся к числу x, то число x
является предельной точкой последовательности {x
k
}. Действительно, в любой ε -
окрестности точки x имеется бесконечно много элементов
подпоследовательности, а стало быть и самой последовательности {x
k
}.
Из леммы 1 следует, что можно дать другое определение предельной точки
последовательности, эквивалентное определению 1.
Определение 2. Точка x бесконечно прямой называется предельной точкой
последовательности {x
k
}, если из этой последовательности можно выделить
подпоследовательность, сходящуюся к x.
Лемма 2. Каждая сходящаяся последовательность имеет только одну предельную
точку, совпадающую с пределом этой последовательности.
Замечание. Если последовательность сходится, то она в силу леммы 2 имеет
только одну предельную точку. Однако, если {x
n
}
не является сходящейся, то она
может иметь несколько предельных точек (и, вообще бесконечно много
предельных точек). Покажем, например, что
{1+(-1)
n
} имеет две предельные
точки.
Действительно,
{1+(-1)
n
}=0,2,0,2,0,2,... имеет две предельные точки 0 и 2,
т.к. подпоследовательности {0}=0,0,0,... и {2}=2,2,2,... этой последовательности
имеют пределами соответственно числа 0 и 2. Других предельных точек у этой
последовательности нет. Действительно, пусть x -любая точка числовой оси,
отличная от точек 0 и 2. Возьмем
ε >0 настолько
-ε 0 ε x-ε x x+ε 2-ε 2 2+ε x
малым, чтобы
ε - окрестности точек 0, x и 2 не пересекались. В ε- окрестностях
точек 0 и 2 содержатся все элементы последовательности и поэтому
ε -
окрестность точки x не может содержать бесконечно много элементов
{1+(-1)
n
} и
поэтому не является предельной точкой этой последовательности.
Теорема. У всякой ограниченной последовательности существует хотя бы одна
предельная точка.
Замечание. Ни одно число x , превосходящее
x
, не является предельной точкой
последовательности {x
n
}, т.е.
x
- наибольшая предельная точка
последовательности {x
n
}.
Пусть x- любое число, превосходящее
x
. Выберем ε>0 настолько малым,
x
′
x
x −ε
x
x
+ε
что x-
ε>
x
.
Так как
{}()(){}
(
)
[
]
,:inf
11
εε
−<≤∈∃>−∀≡= xxxxxxxxx
def
и x
1
∈{x}, правее x
1
лежит конечное число элементов последовательности {x
n
}
или их вовсе нет, т.е. x не является предельной точкой последовательности {x
n
}.
Определение. Наибольшая предельная точка
x
последовательности {x
n
}
называется верхним пределом последовательности и обозначается символом
n
n
xx
0
lim
→
= . Из замечания следует, что у всякой ограниченной последовательности
есть верхний предел.
Аналогично вводится понятие нижнего предела
n
n
xx
∞→
=
lim (как наименьшей
предельной точки последовательности {x
n
}).
Итак, мы доказали следующее утверждение. У всякой ограниченной
последовательности существует верхний и нижний пределы.
Сформулируем без доказательства следующую теорему.
Теорема. Для того, чтобы последовательность {x
n
} была сходящейся, необходимо
и достаточно, чтобы она была ограниченной и чтобы ее верхний и нижний
пределы
xx è совпадали.
Результаты этого пункта приводят к следующей основной теореме Больцано-
Вейерштрасса.
Теорема Больцано-Вейерштрасса. Из любой ограниченной последовательности
можно выделить сходящуюся подпоследовательность.
Доказательство. Так как последовательность {x
n
} ограничена, то она имеет хотя
бы одну предельную точку x. Тогда из этой последовательности можно выделить
подпоследовательность, сходящуюся к точке x (следует из определения 2
предельной точки).
Замечание. Из любой ограниченной последовательности можно выделить
монотонную сходящуюся последовательность.
4.3. Понятие функции. Предел функции. Непрерывность
4.3.1. Определение функции
Определение 1.
Пусть даны два непустых подмножества {x}и {y}множества R.
Если каждому элементу x из {x} ставится в соответствие один элемент y из {y},
то y называется функцией f (отображением) аргумента x. Это записывается в
виде:
(
)
{
}
(
)
{
}
xxxfyxxxfy
∈
=
∈
∀
= , èëè ,
.
Другими словами, с помощью функции y=f(x) подмножество {x} отображается в
подмножестве {y}, поэтому допустима запись
(
)
{
}
., a xxxfx
∈

Подмножество {x} или D(f) называется областью определения функции y,
подмножество {y} или E(f) - множеством ее значений. Аргумент x часто
называют независимой переменной, функцию y -зависимой переменной, а
соответствие между ними- функциональной зависимостью.
Частным значением функции y=f(x) при x=a, a
∈{x} называется то значение y ,
которое соответствует заданному значению x. Оно обозначается через f(a), или
y
|
x=a
.
Функции могут быть заданы аналитически, графически и с помощью
таблиц.
4.3.2. Способы задания функций
Функция задана аналитически , если функциональная зависимость выражена в
виде формулы, которая указывает совокупность тех математических операций,
которые должны быть выполнены, чтобы по данному значению аргумента найти
соответствующее значение функции.
Пример 1. Функция Дирихле
.
()
∉
∈
==
Qx
Qx
xDy
ïðè 0
ïðè 1
Пример 2. (рис.1)
<−
0 ïðè 1 x
x
=
>
==
0 ïðè 0
0 ïðè 1
sgn
x
õ
xy
y
1
-1
Рис.1
Определение 2. Графиком функции y=f(x), x
∈{x} называется геометрическое
место точек на плоскости с координатами (x,f(x)), где x
∈{x}.
Графический способ задания функции, помимо геометрического изображения
функции, заданной уравнением, удобен тогда, когда функцию трудно задать
аналитически. Задать функцию графически - это значит задать ее график.
При табличном способе задания функции рядом с числовым значением
аргумента выписывается соответствующее значение функции. Недостатком
табличного способа задания функции является то, что в таблице могут быть
указаны не все, а лишь отдельные значения аргумента и функции. Особенности
изменения функции при этом могут быть искажены.
4.3.3. Монотонные функции
Пусть функция y=f(x) определена на множестве {x} и точки
x
1
,x
2
∈{x}любые точки, связанные соотношением x
1
< x
2
.
Тогда
() ()()()
() ()()()
()
;ìîíîòîííà
âîçðàñòàåò íå
óáûâàåò íå
2121
2121
xf
xfxfxfxx
xfxfxfxx
def
def
def
≡
≡≥⇒<
≡≤⇒<
