Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

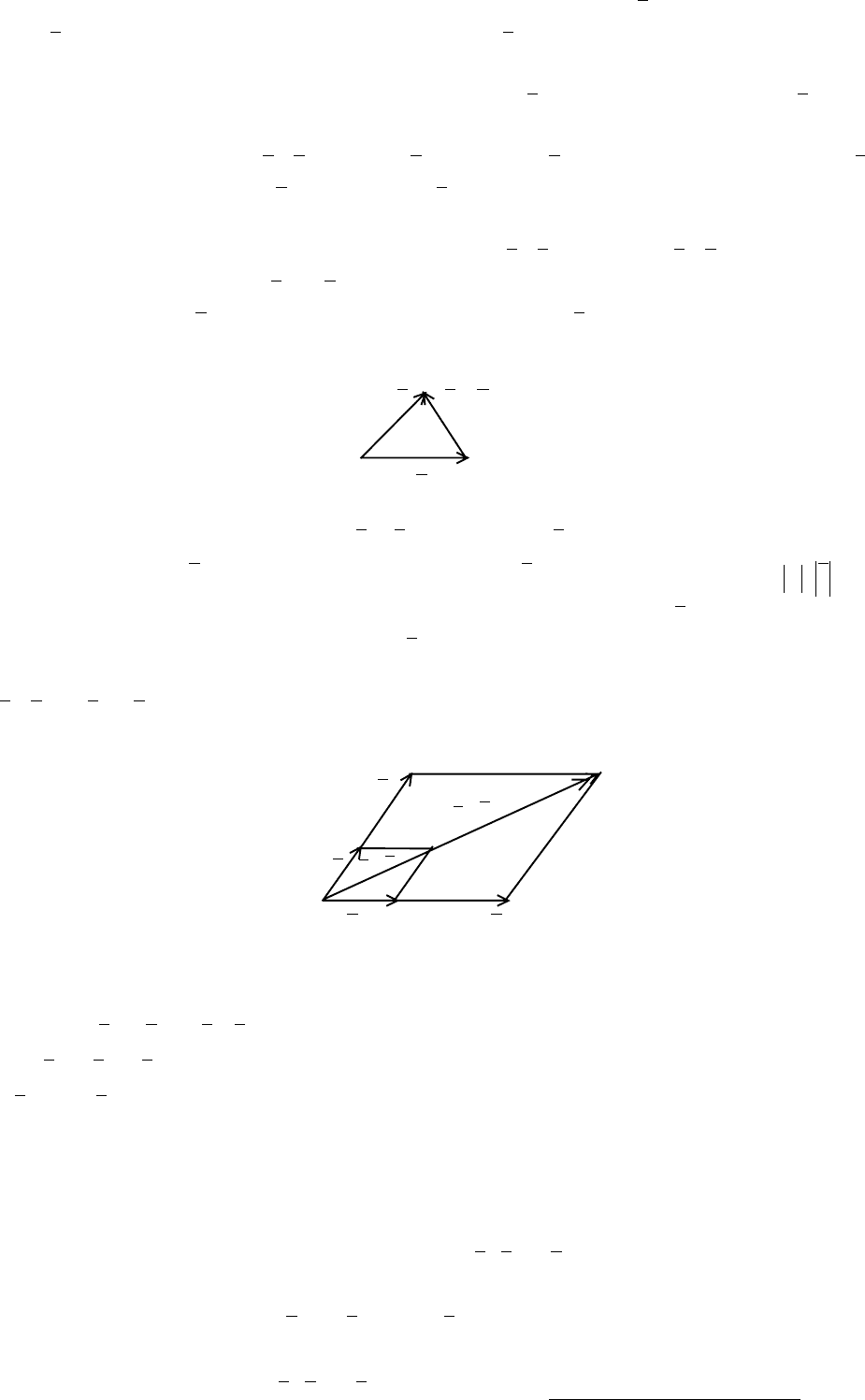
Для доказательства этого свойства определим вектор -a , противоположный
вектору
a , как вектор, коллинеарный вектору a , имеющий с ним одинаковую
длину и противоположное направление.
Взятая по определению 1 сумма вектора
a с таким вектором -a дает
нулевой вектор.
Определение 2. Разностью
ba − вектора a и вектора b называется такой вектор c ,
который в сумме с вектором
b дает вектор a .
Из определения 2 и из правила треугольника (определение 1) сложения
векторов вытекает правило построения разности
ba − : разность ba − приведенных
к общему началу векторов
a и b представляет собой вектор, идущий из конца
вычитаемого вектора
b в конец уменьшаемого вектора a .
a
ab−
0
b
Определение 3. Произведением α⋅a (a ⋅α) вектора a на вещественное число α
называется вектор
b , коллинеарный вектору a , имеющий длину a⋅
α
, и
имеющий направление, совпадающее с направлением вектора
a в случае α>0 и
противоположное направлению вектора
a в случае α<0.
Свойства операции умножения вектора на число:
5.
ba)ba(
ααα
+=+
αa
α()ab+
a
ab+
0
b
αb
При “растяжении” сторон параллелограмма в α раз в силу свойств подобия
диагональ также “растягивается” в α раз, т.е.
(
)
baba +=+
ααα
6.
()
aaa
βαβα
+=+ .
7.
(
)
()
aa
αββα
= .
Последние два свойства очевидны из геометрических соображений.
1.1.3. Понятие линейной зависимости векторов
Линейной комбинацией n векторов
n21
a,,...a,a будем называть сумму
произведений этих векторов на произвольные вещественные числа:
nn2211
a...aa
α
α
α
+
+
+
; (1)
где α
1,
α
2,...
α
n-
любые вещественные числа.
Определение 1. Векторы
n21
a,...,a,a называются линейно зависимыми, если
найдутся такие вещественные числа α
1,
α
2,...,
α
n,
из которых хотя бы одно отлично

от нуля, что линейная комбинация векторов
n21
a,...,a,a с указанными числами
обращается в нуль:
0a...aa
nn2211
=
+
+
+
α
α
α
Векторы
n21
a,...,a,a
не являющиеся линейно зависимыми будем называть
линейно независимыми
.
Приведем другое определение линейно независимых векторов.
Определение 2. Векторы
n21
a,...,a,a называются линейно независимыми, если
равенство нулю их линейной комбинации (1) возможно лишь в случае, когда
числа α
1
=α
2
=,...,=α
n
=0
Из определений 1 и 2 следуют два утверждения:
1. Если хотя бы один из векторов
n21
a,...,a,a
является нулевым, то эти
векторы являются линейно зависимыми.
2. Если среди n векторов какие-либо (n-1) векторов линейно зависимы, то и
все n векторов линейно зависимы.
1.1.4. Линейные комбинации двух векторов
Необходимым и достаточным условием линейной зависимости двух
векторов является их коллинеарность.
Доказательство. 1). Необходимость. Пусть векторы
b è a линейно зависимы.
Докажем их коллинеарность.
По определению линейной зависимости найдутся такие вещественные числа
α и β, хотя бы одно из которых не равно нулю, что справедливо равенство
0ba =+
βα
Пусть β≠0. Тогда
ab
β
α
−= .
Обозначив
β
α
λ
−= ; получим ab
λ
= .
Необходимость доказана.
02). Достаточность. Пусть векторы
a
b
и коллинеарны. Докажем, что они линейно
зависимы. Если хотя бы один из них нулевой, то
a
b
и линейно зависимы.
Если же вектор
a ненулевой, то из коллинеарности векторов a
b
и следует,
что
b=λa т.е.
)
(
ab+− =1λ , ч.т.д. 0
Следствие 1. Если векторы
a
b
и не коллинеарны, то они линейно независимы.
Следствие 2. Среди двух неколлинеарных векторов не может быть нулевого
вектора.
1.1.5. Линейные комбинации трех векторов
Определение. Векторы называются компланарными, если они лежат либо в
одной плоскости, либо в параллельных плоскостях.
Теорема. Необходимым и достаточным условием линейной зависимости трех
векторов является их компланарность.
Доказательство. 1). Необходимость. Пусть три вектора
abc,, линейно зависимы.
Докажем их компланарность.
По определению линейной зависимости найдутся такие вещественные числа
α, β и γ, хотя бы одно из которых отлично от нуля, что

αβγabc++=0.
Пусть γ≠0. Тогда
ca=− −
α
γ
b
β
γ
.
Обозначив λ= −
α
γ
, µ= −
β
γ
, имеем ca=+λµb. Если все три вектора приложены к
общему началу О, то отсюда следует, что вектор
c равен диагонали
параллелограмма, построенного на векторах
λµab и
B C
µb
c
b
0 A
a
λa
Рис. 1
Но это означает, что векторы
abc,, лежат в одной плоскости, т.е.
компланарны.
2). Достаточность. Пусть векторы
ab c, и компланарны. Докажем, что они
линейно зависимы.
Если какая-нибудь пара из указанных трех векторов коллинеарна, то эта
пара линейно зависима и все три вектора
ab c, и линейно зависимы.
Осталось рассмотреть случай, когда в тройке векторов
ab c, и ни одна пара
векторов не коллинеарна.
Перенесем три компланарных вектора
ab c, и на одну плоскость и приведем
их к общему началу О (рис.1). Через конец C вектора
c проведем прямые,
параллельные векторам
a
b
и . Обозначим А точку пересечения прямой,
параллельной вектору
b
с прямой, на которой лежит вектор a , а В - точку
пересечения прямой, параллельной вектору
a , с прямой, на которой лежит
вектор
b
. (Точка пересечения существует, т.к. векторы a
b
и не коллинеарны.)
OBOAC +=
Т.к. вектор
OA коллинеарен ненулевому вектору a , то
aOA
λ
= .
Аналогично
bOB
µ
= , т.е. bac
µλ
+= .
Или
)(
01 =−++ cba
µλ
, ч.т.д.
Следствие 1. Каковы бы ни были неколлинеарные векторы
a и b , для любого
вектора
c , лежащего в одной плоскости с векторами a и b , найдутся такие
вещественные числа λ и µ, что
bac
µλ
+= .
Следствие 2. Если векторы
a , b и c не компланарны, то они линейно
независимы.
1.1.6. Линейная зависимость четырех векторов
Теорема. Любые четыре вектора линейно зависимы.

Доказательство. Исключим случай, когда какая-нибудь тройка из данных
четырех векторов компланарна, т.к. тогда указанная тройка линейно зависима и,
следовательно, все четыре вектора линейно зависимы.
Осталось рассмотреть случай, когда среди четырех векторов
abc d, и , никакая тройка векторов не компланарна.
Приведем все четыре вектора к общему началу О и проведем через конец D
вектораd плоскости, параллельные плоскостям, определяемым парами
векторов
bc ac ab, и .
D
d
С
B E
b
с
0
a
A
OCOBOAd ++= .
cOCbOBaOA
γµλ
=== ,, .
Следовательно,
dab=++λµγc.
Или
)
(
λµγabc d+++−=10, ч.т.д.
Следствие. Каковы бы ни были некомпланарные векторы
ab c, и , для любого
вектора
d найдутся такие вещественные числа α, µ и γ, что справедливо
равенство
dab=++λµγc.
1.1.7. Понятие базиса. Аффинные координаты
Определение 1. Три линейно независимых вектора
ab c, и образуют в
пространстве базис, если любой вектор
d может быть представлен в виде
линейной комбинации векторов ab c, и .
Аналогично определяется базис на плоскости π.
Определение 2. Два лежащих в плоскости π линейно независимых вектора
a
b
и
образуют на этой плоскости базис, если любой лежащий в этой плоскости вектор
с может быть представлен в виде линейной комбинации векторов a
b
и .
Имеют место следующие фундаментальные утверждения:
1). любая тройка некомпланарных векторов
ab c, и образует базис в
пространстве;
2). любая пара лежащих в данной плоскости неколлинеарных векторов
a
b
и
образует базис на этой плоскости.
Теорема. Каждый вектор
d может быть единственным способом разложен по
базису
abc,,:
dab=++λµγc.
Числа λ, µ, γ называются координатами вектора
d относительно базиса abc,,.
Доказательство. Пусть таких разложений два:
dab=++λµγc b и dab=++λµγ
111
c
Вычитая почленно получаем
()
(
)
(
)
λλ µµ γγ−+−+−=
111
0abc.
В силу линейной независимости базисных векторов
abc,,:
λλ µµ
γ
γ
λ
λ
µ
µ
γ
γ
−=
111 11
0 , - = 0, - = 0, или =,= = ,
1
.

Единственность разложения по базису доказана.
Теорема. При сложении двух векторов
dd
1
и
2
их координаты складываются. При
умножении вектора
d
1
на любое число α все его координаты умножаются на это
число.
Доказательство. Пусть
dabc
1111 2 2 2
=++λµγ λµ γ, d = a+ b+ c
2
.
Тогда в силу свойств линейных операций
()
(
)
(
)
dd a b
12 12 12 12
+= + + + + +λλ µµ γγc.
(
)
(
)
(
)
ααλ αµ αγdab
11 1 1
=++c.
В силу единственности разложения по базису теорема доказана.
Аффинные координаты в пространстве определяются заданием базиса
abc,, и некоторой точки О, называемой началом координат.
Аффинными координатами любой точки М называются координаты вектора
OM (относительно базиса c,b,a ).
Свойства базиса и понятие аффинных координат на плоскости аналогичны
случаю пространства.
1.1.8. Проекция вектора на ось
Определение. Проекцией вектора
BAa = на ось U называется величина
направленного отрезка
11
BA
11
BA оси U, где - основания перпендикуляров, опущенных
на ось U из точек A и B соответственно.
B
A
U
′
A
′
B
Теорема 1.8. Проекция вектора
a на ось U равна длине вектора a , умноженной на
косинус ϕ угла наклона вектора
a к оси U.
Доказательство
a B
A ϕ C V
′
A
′
B U
Обозначим через V ось,
проходящую через начало A
вектора
a и имеющую тоже
направление, что и ось U, и
пусть C - проекция B на ось V.
∠BAC=ϕ, = AC.
11
BA
Т.к. по определению пр
и
11
BAa = , то пр
и
ACa
=
.
Но
BAAC = cosϕ= a cosϕ. Следовательно пр
и
ϕ
cosaa = , ч.т.д.
1.1.9. Декартова прямоугольная система координат в пространстве (ДПСК)
ДПСК является частным случаем аффинной системы, отвечающим тройке
взаимно ортогональных и единичных базисных векторов
k,j,i . Принято
направления векторов
k,j,i брать совпадающими с направлением декартовых осей
Ox, Oy, Oz соответственно.

Нами получено, что любой вектор d может быть, причем единственным
способом, разложен по декартову прямоугольному базису (ДПБ)
k,j,i , т.е. для
каждого вектора
d существует единственная тройка чисел X, Y, Z такая, что
kZjYiXd ++= .
Числа X, Y, Z называются декартовыми прямоугольными координатами
(ДПК) вектора
d . Если M- любая точка пространства, то ДПК этой точки
совпадают с ДПК вектора
MO .
Вектор
kZjYiX ++=d будем также записывать в виде
{}
Z,Y,Xd = .
Теорема 1.9. ДПК вектора
d равны прекциям этого вектора на оси OX, OY и OZ
соответственно.
Доказательство
D
d
С
B
k
j
0
i
A
COBOAOd ++= .
kZCO,jYBO,iXAO ===
XOA
=
, т.к. из iXOA = и того,
что
1i = , получаем XOA = .
Но знаки OA и X совпадают,
т.к. когда векторы
i è AO направлены в одну сторону оба числа OA и X
положительны, а в случае когда векторы
i è AO направлены в противоположные
стороны, оба числа OA и X отрицательны. Т.е. OA=X.
Аналогично OB=Y, OC=Z, ч.т.д.
Обозначим α, β, γ углы наклона вектора
d к осям Ox, Oy, Oz
соответственно. Числа cosα, cosβ, cosγ называют направляющими косинусами
вектора
d .
Из теорем 8 и 9 имеем
γβα
cosd= Z,cosd=Y ,cosdX = (1)
Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов его сторон, то из равенств OA=X, OB=Y, OC=Z получим выражение
для длины вектора
d через его координаты:
222
ZYXd ++= (2)
Из формул (1) и (2) имеем:
222222
Z+Y+X
Y
=cos ,
ZYX
X
cos
βα
++
=
,
222
ZYX
Z
cos
++
=
γ
.
Возводя в квадрат и складывая последние равенства получим
1coscoscos
222
=++
γββ
1.2. Скалярное произведение двух векторов
1.2.1. Определение скалярного произведения (СП)
Определение 1. СП двух векторов называется число, равное произведению длин
этих векторов на косинус угла между ними.
Скалярное произведение будем обозначать символом
(
)
ba ⋅ , угол между
векторами
b è a - ϕ.

По определению 1 :
()
ϕ
cosbaba ⋅⋅=⋅ (1)
Можно сформулировать другое определение СП двух векторов,
эквивалентное определению 1.
Из теоремы 1.8 имеем:
ϕ
cosb=bïð
a
(проекция вектора
b на ось вектора a ).
Отсюда получаем Определение 2:
(
)
b•ðaba
a
⋅=⋅ или
(2)
(
)
a•ðbba
b
⋅=⋅
1.2.2. Геометрические свойства СП
Теорема 2.1. Необходимым и достаточным условием ортогональности двух
векторов является равенство нулю их скалярного произведения.
Доказательство. 1) Необходимость. Пусть векторы
b è a ортогональны, ϕ - угол
между ними. Тогда cosϕ=0 и, в силу формулы (1)
(
)
0ba =⋅
2. Достаточность. Пусть
(
)
0ba =⋅ . Докажем, что векторы b è a ортогональны. Если
хотя бы один из векторов
b èëè a является нулевым, то он ортогонален любому
вектору.
Если же векторы
b è a ненулевые, то 0b , 0a 〉〉 , поэтому из равенства
()
0cosbaba =⋅=⋅
ϕ
вытекает, что cosϕ=0, т.е. векторы ортогональны, ч.т.д.
Замечание.
Углом между двумя векторами считаем тот, который не превосходит π. (0 ≤
ϕ ≤π)
Из формулы (1) следует
Теорема 2.2. Два ненулевых вектора
b è a составляют острый (тупой) угол тогда и
только тогда, когда их СП положительно(отрицательно).
1.2.3. Алгебраические свойства СП
1.
(
)
(
)
abba ⋅=⋅
2.
()
(
)
(
)
baba ⋅=⋅
αα
3.
(
)
()
(
)
cbcacba ⋅+⋅=+
4.
()
0aa >⋅ , если a - ненулевой вектор, и
()
, если 0aa =⋅ a - нулевой вектор.
Свойство 1. Следует из формулы (1).
Второе свойство получается из определения 2 (формула 2) скалярного
произведения:
()
()
(
)
(
)
baaðïbaðïbba
bb
⋅=⋅=⋅=
αααα
.
Свойство 3. получаем из свойств линейности проекции вектора на ось
(
)
bðïaðïbaðï
ccc
+=+ и формулы (2):

() ()
(
)
()
()
cbca
bðïcaðïcbðïaðïcbaðïccba
ccccc
⋅+⋅=
=+⋅=+⋅=+⋅=⋅+
Четвертое свойство вытекает из формулы (1):
(
)
2
aaa =⋅ .
1.2.4. Выражение скалярного произведения (СП) в декартовых прямоугольных
координатах (ДПК)
Теорема 2.4. Если два вектора
b è a определены своими ДПК
{
}
111111
Z,Y,XkZjYiXa =++=
{
}
2, 2, 2222
ZYXkZjYiXb =++= ,
то СП этих векторов равно сумме попарных произведений их соответствующих
координат:
(
)
212121
ZZYYXXba ++=⋅ .
Доказательство. По определению 1
(
)
11110cosiiii =⋅⋅=⋅⋅=⋅ ,
также
(
)
(
)
1kk ,1jj =⋅=⋅ .
()
0011
2
cosjiji =⋅⋅=⋅⋅=⋅
π
, также
(
)
(
)
(
)
(
)
(
)
0jkikkjijki =⋅=⋅=⋅=⋅=⋅ .
Используя алгебраические свойства СП имеем
(
)
(
)
(
)
(
)
(
)
(
)
() () () ()
21212121212121
2121212121
ZZYYXXkkZZjkYZikXZkjZY
jjYYijXYkiZXjiYXiiXXba
++=⋅+⋅+⋅+⋅+
+⋅+⋅+⋅+⋅+⋅=⋅
Следствие 1. Необходимым и достаточным условием ортогональности векторов
{}
111
Z,Y,Xa = и
{
222
Z,Y,Xb =
}
является равенство
0ZZYYXX
212121
=
+
+
Следствие 2. Угол ϕ между векторами
b è a определяется по формуле
2
2
2
2
2
2
1
2
1
2
1
2
212121
ZYXZYX
ZZYYXX
cos
++++
+
+
=
ϕ
1.3. Векторное произведение двух векторов
1.3.1. Правые и левые тройки векторов и системы координат
Определение 1. Три вектора называются упорядоченной тройкой (или просто
тройкой), если указано какой из них является первым, какой- вторым и какой-
третьим.
Т.е. запись
cba означает, что первым элементом является вектор a , вторым
-
b , третьим - c .
Определение 2. Тройка некомпланарных векторов
cba называется правой
(левой), если после приведения к общему началу вектор
c располагается по ту
сторону от плоскости, определяемой векторами
b è a , откуда кратчайший поворот
от
b ê a виден совершающимся против часовой стрелки (по часовой стрелке).
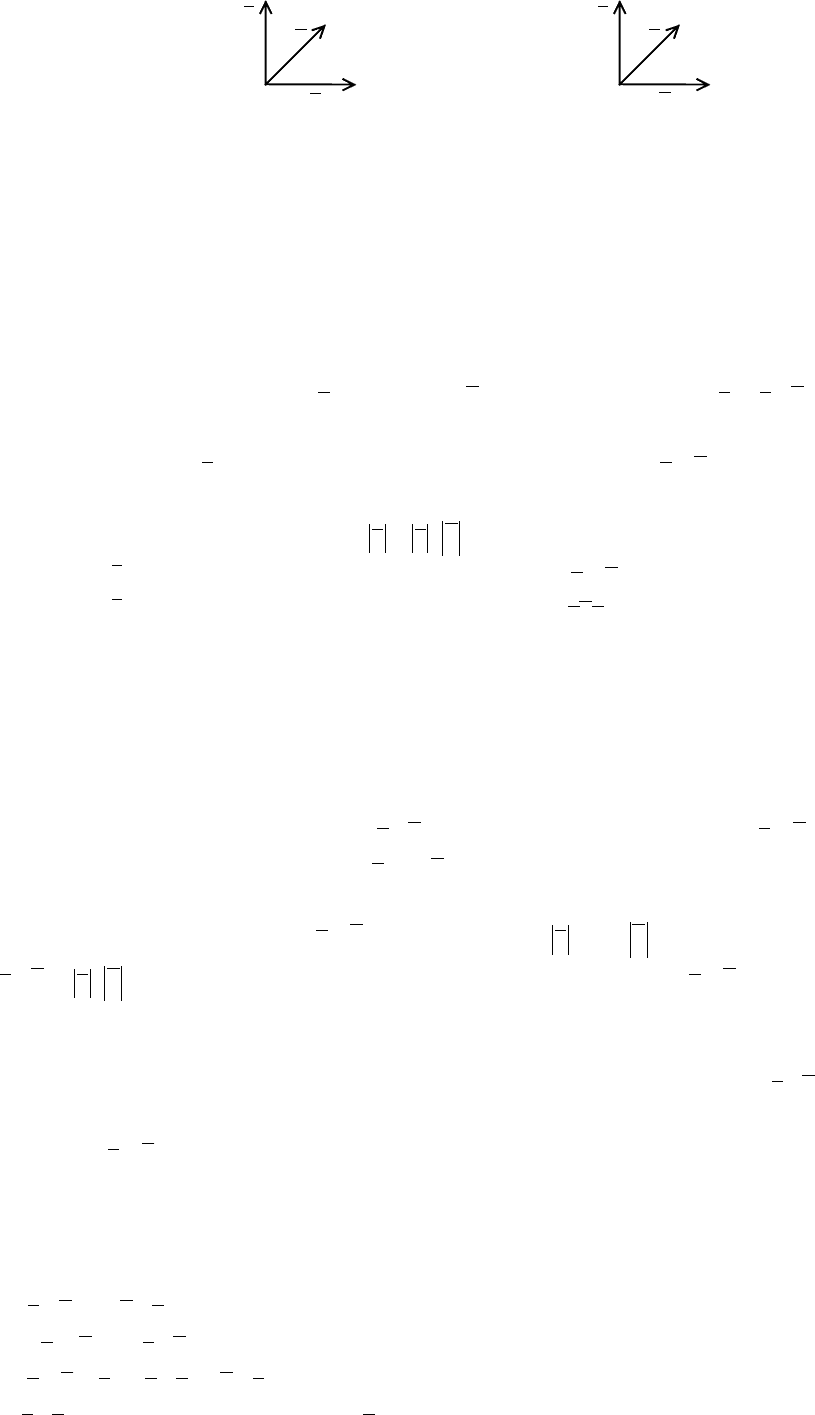
c
b
a
c
a
b
Правая тройка Левая тройка
Определение 3. Аффинная или декартова система координат называется правой
(левой), если три базисных вектора образуют правую (левую) тройку.
В дальнейшем будем рассматривать только правые системы координат.
1.3.2. Векторное произведение двух векторов (ВП)
Определение. ВП вектора
a на вектор b называется вектор
[
]
bac ×= ,
удовлетворяющий трем условиям:
1) длина вектора
c равна произведению длин векторов b è a на синус угла ϕ
между ними:
ϕ
sinbac ⋅⋅= (1)
2) вектор
c ортогонален к каждому из векторов b è a ;
3) вектор
c направлен так, что тройка векторов cba является правой.
1.3.3. Геометрические свойства ВП
Теорема 3.3. Необходимым и достаточным условием коллинеарности двух
векторов является равенство нулю их ВП.
Доказательство. 1). Необходимость вытекает из определения ВП.
2). Достаточность. Пусть
[
]
0ba =× . Докажем, что векторы b è a коллинеарны.
Если хотя бы один из векторов
b èëè a является нулевым, то он коллинеарен
любому вектору.
Если же оба вектора
b è a ненулевые, то 0a > , 0b > и поэтому из равенства
[]
0sinbaba =⋅⋅=×
ϕ
следует, что sinϕ=0, ϕ=0, т.е. векторы b è a коллинеарны, ч.т.д.
Заметим, что так как площадь параллелограмма равна произведению
смежных сторон этого параллелограмма на синус угла между ними, то из
определения ВП (пункт 1) получим, что длина (или модуль) ВП
[
]
ba × равняется
площади параллелограмма, построенного на приведенных к общему началу
векторах
b è a .
1.3.4. Алгебраические свойства векторного произведения (ВП)
Из определения ВП получаем следующие четыре свойства ВП:
1.
[
]
[
]
abba ×−=× ;
2.
()
[
]
[
]
baba ×=×
αα
;
3.
(
)
[
]
[]
[
]
cbcacba ×+×=×+ ;
4.
[
для любого вектора
]
0aa =× a .
1.3.5. Понятие матрицы и определителя второго и третьего порядка
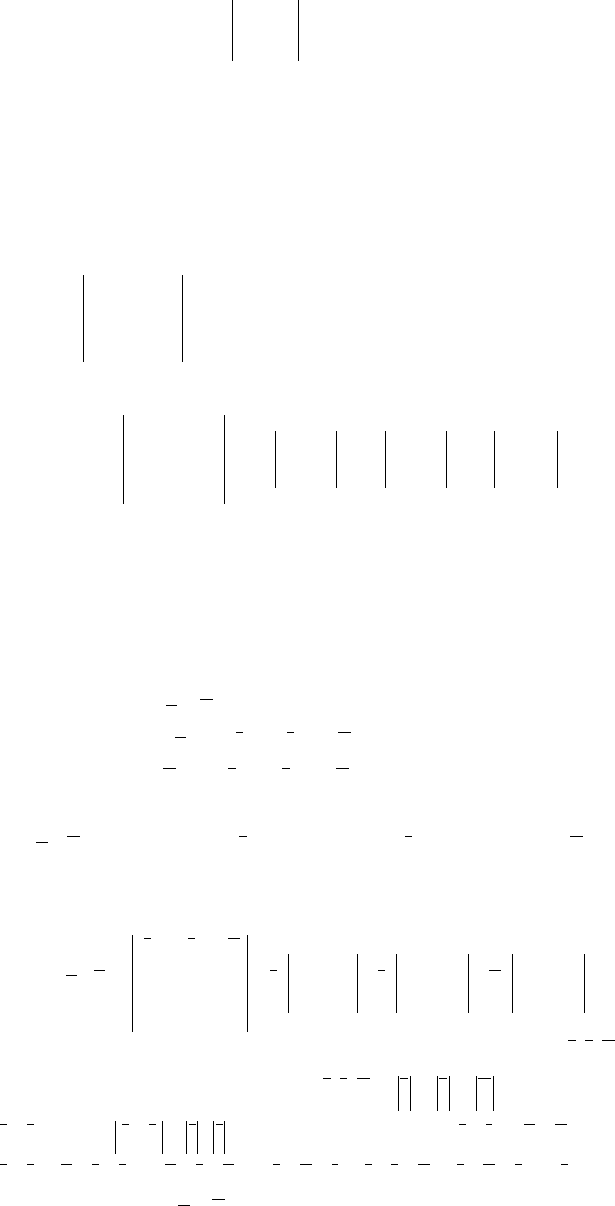
Прямоугольную таблицу из чисел, содержащую m строк и n столбцов
называют матрицей.
Если число строк матрицы совпадает с числом ее столбцов, то матрица
называется квадратной.
Числа, входящие в состав матрицы называют ее элементами.
Рассмотрим квадратную матрицу, состоящую из четырех элементов:
2
2
11
ba
ba
.
Определителем второго порядка, соответствующим этой матрице
называется число, равное
a и обозначаемое символом
1221
bab −
1221
22
11
baba
ba
ba
−=
.
Рассмотрим квадратную матрицу, состоящую из девяти элементов:
333
222
111
cba
cba
cba
.
Определителем третьего порядка, соответствующим этой матрице называется
число, обозначаемое символом ∆ и равное
321321321321321321
333
222
111
bcacababcbacacbcba
cba
cba
cba
−−−++==∆
Последнюю формулу для удобства запоминания можно записать в виде:
33
22
1
33
22
1
33
22
1
333
222
111
ba
ba
c
ca
ca
b
cb
cb
a
cba
cba
cba
⋅+⋅−⋅==∆
.
Такая запись называется разложением определителя ∆ по элементам первой
строки.
1.3.6. Выражение векторного произведения (ВП) в декартовых прямоугольных
координатах (ДПК)
Теорема. Если два вектора
b è a определены своими ДПК
{
}
111111
Z,Y,XkZjYiXa =++=
{
}
222222
Z,Y,XkZjYiXb =++= ,
то их ВП имеет вид
[
]
()
(
)
(
)
kYXYXjXZXZiZYZYba
122112211221
−+−+−=× (1)
Для запоминания этой формулы удобно использовать символ определителя
(см. предыдущий пункт) и переписать ее в виде
[]
22
11
22
11
22
11
222
111
YX
YX
k
ZX
ZX
j
ZY
ZY
i
ZYX
ZYX
kji
ba ⋅+⋅−⋅==×
.
Доказательство теоремы. Учитывая, что базисные векторы
k,j,i взаимно
ортогональны, образуют правую тройку
kji k,j,i == , имеем
[] []
[
]
[
]
[] [] [] [][][]
−=×=×=×−=×−=×=×
=×=×=⋅⋅=⋅=×=×
ijk ,ikj ,jik ,jki ,kij ,kji
0kkjj æå òàê, 00110siniiii ò.ê.0ii
(2)
Перемножая векторно
b è a , получим
