Неверов В.Н., Титов А.Н. Физика низкоразмерных систем

Подождите немного. Документ загружается.

149

Это указывает на выполнение условия

≈

в случае введения примеси Cr в Al.

Следовательно, модель ВСС, согласно которой заряд примеси

∆ равняется

количеству d-электронов атома примеси, подтверждается экспериментально.

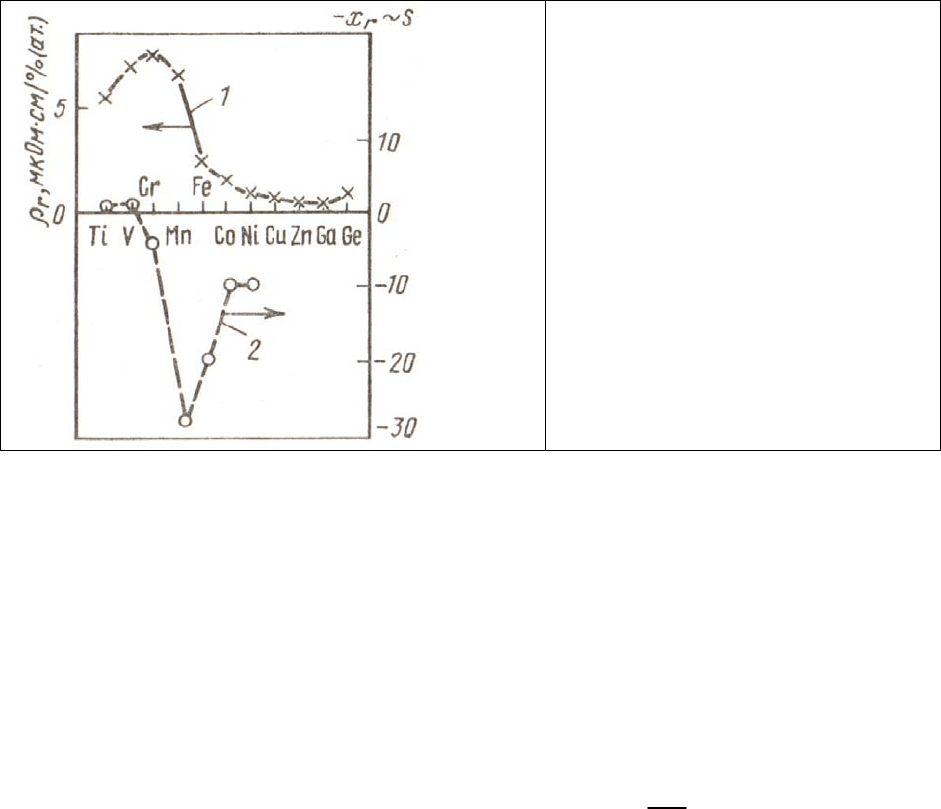
Рис. 3.3. Остаточное

сопротивление (из-за рассеяния на

нейтральной примеси)

, кривая 1

и термоЭДС (кривая 2) в

разбавленных алюминиевых

сплавах. Вместо абсолютного

значения термоЭДС построен

экспериментальный параметр x

S [1.3].

Измерения термоЭДС

S этих сплавов также свидетельствует в пользу теории

ВСС. Действительно, абсолютная примесная термоЭДС должна изменять свой знак в

точке

≈ , поскольку при меньших значениях

носители заряда в полосе ВСС

можно рассматривать как электроны, а при больших – как дырки. Как видно из Рис.3.3.

S изменяет свой знак где-то между V и Cr, т.е. таком значении

∆ , которое

соответствует максимуму

. С другой стороны, как следует из формулы (5.3),

величина

S зависит как от фазового сдвига

, так и от Г. Если предположить, что Г

одинакова для всех сплавов (что является довольно грубым приближением), то

отрицательный экстремум

S должен возникнуть при

= , т.е. при

∆ = 7,5

(см. формулу (2.3)). Если

∆ равно числу d-электронов, то эта ситуация должна

возникнуть для атомов Fe, что как раз и совпадает с результатом, показанным на Рис.

3.3.

Другой вариант проверки модели ВСС состоит в том чтобы измерить одну из

величин, контролирующихся параметром

−

как функцию

. Такие измерения

выполнены для магнитной восприимчивости системы Ag

TiS

в зависимости от

содержания серебра, определяющего концентрацию электронов проводимости в зоне

TiS

и, следовательно, величину

. Они показаны на Рис. 4.3., где точки получены

экспериментально, а линия проведена по формуле (10.3), т.е. по модели ВСС при

значениях параметров:

− = 0,355 эВ, Г = 0,002 эВ.

150

Рис. 4.3. Концентрационная

зависимость восприимчивости

свободных электронов Ag

TiS

. Точки –

эксперимент, линия – подгонка по

формуле (10.3). Значение

определяется из соотношения

)(

2/1 e

WFn

- плотность

состояний зоны проводимости,

)(

2/1 e

- интеграл Ферми степени ½.

Увеличение концентрации электронов

соответствует увеличению заполнения

зоны проводимости и, следовательно,

росту

Таким образом, измерения электронных свойств -

S , электронной

теплоёмкости

c∆

и магнитной восприимчивости

позволяют получить основные

параметры модели ВСС для конкретного материала. Для сплавов на основе алюминия

результаты суммированы в Таблице 1.3.

Видно, что и ширина ВСС-зоны и её положение относительно уровня Ферми

могут изменяться в широких пределах.

3.4. Магнитные примеси и ВСС

Как видно из Таблицы 1.3., большинство изучаемых примесей являются 3d-

металлами. Это не удивительно, поскольку для металлов с меньшим значением

орбитального числа l ширина зоны ВСС столь велика, что локализация становится

незаметна. С другой стороны, известно, что 3d- неспаренные электроны являются

источником магнитного момента иона примеси. Каково же должно быть влияние этого

обстоятельства на форму

зоны ВСС?

Ясно, что из-за взаимодействия с магнитным моментом иона примеси энергия

электронов начнёт зависеть от ориентации их собственного магнитного момента.

Следовательно, единая полоса ВСС расщепится на две, соответствующие разным

.Примесь Г, эВ

(

− ), эВ

Ti 23,4 10.0

V 20,9 6,3

Cr 0,46 ~ 0

Mn 0,36 - 0,04

0,54 ~ 0

Fe 1,17 - 0,43

Co 2,57 - 1,16

Ni 2,0 - 2,11

Таблица 1.3. Значения ширины

зоны ВСС Г и её положение

относительно уровня Ферми

(

−

) для примесей

151

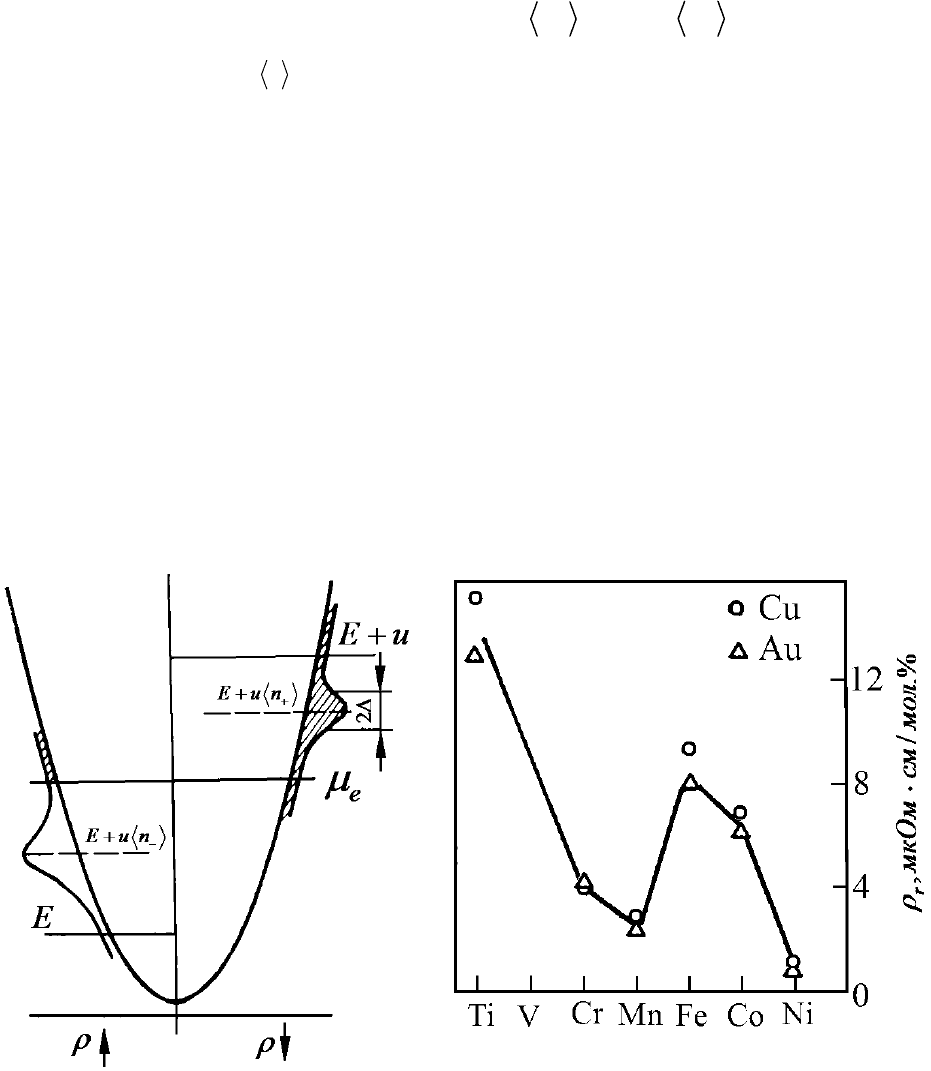
ориентациям спинов электронов, экранирующих ион примеси. Виртуальные d-уровни

шириной

2∆ возникнут [2.3] при энергиях

Eun

−

Eun

, где E = E

, как это

показано на Рис. 5.3, а

nu - энергия обменного взаимодействия примеси с электронами

нижней и верхней подзон. Число электронов на этих уровнях можно подсчитать по

величине незаштрихованной площади под линией

, обозначающей уровень Ферми.

Легко видеть, что расщепление из-за обменного взаимодействия, энергетически выгодно,

поскольку большая часть электронов в нижней подзоне понижает свою энергию, тогда как

повышают свою энергию только электроны верхней позоны, заполнение которой не

может быть больше чем у нижней. Ясно, что максимальный выигрышь в энергии

получается когда нижняя

подзона полностью заполнена, а верхняя полностью пуста. Это

достигается при попадании полосы ВСС точно на уровень Ферми:

= и при условии

превышения обменной энергией величины Г. Последнее означает, что величина

расщепления должна быть больше полуширины полосы ВСС.

Рис. 5.3. Магнитное расщепление

полосы ВСС

Рис. 6.3. Остаточное электросопротивление

разбавленных твёрдых растворов на основе

меди и золота.

Поскольку спиновое расщепление полосы ВСС приводит к формированию двух

полос при разной энергии относительно уровня Ферми, то монотонное увеличение как

концентрации электронов при постоянном значении

∆

, так и

∆

при постоянстве

должно дважды приводить к возможности пересечения уровнем Ферми экстремумов

плотности состояний. Следовательно, должны наблюдаться две аномалии всех свойств –

152

магнитной восприимчивости свободных электронов, электросопротивления, термоЭДС,

теплоёмкости электронной подсистемы и пр. Действительно, как видно из Рис. 6.3., такое

поведение электросопротивления подтверждается экспериментально.

Взаимодействие магнитного момента электронов в спиново-расщеплённых

подзонах ВСС с магнитным моментом примеси приводит к установлению определённой

их взаимной ориентации. Вообще говоря, такая ориентация может быть как

ферромагнитной, когда моменты

ориентированы одинаковым образом, так и

антиферромагнитной, когда моменты направлены в противоположные стороны. Но на

малых расстояниях, как правило, оказывается более выгодной антиферромагнитная

ориентация. Это означает, что наблюдаемый магнитный момент примеси будет частично

скомпенсирован ВСС-электронами. Однако, большая ширина подзон при умеренных

температурах делают этот эффект почти всегда незначительным.

3.5. Эффект Кондо

Кондо рассмотрел рассеяние электронов проводимости на атоме примеси,

окружённом «шубой» ВСС – электронов. Он обнаружил, что важную роль в рассеянии

играет процесс, схематически показанный на Рис. 7.3. Электрон проводимости со спином

противоположным спину ВСС – электрона налетает на примесь, окружённую «шубой»

локализованных электронов. Он не может принять участие в экранировании, поскольку

примесь вместе «шубой

» уже нейтральны, так, что его появление в составе «шубы»

вызовет увеличение энергии U за счёт кулоновского отталкивания. Однако, в результате

взаимодействия с «шубой» он выбивает один из электронов «шубы» на уровень Ферми и

занимает его место, одновременно изменяя ориентацию спина примеси, так, что общий

спин системы сохраняется. В итоге, на уровне

Ферми оказывается электрон с

«опрокинутым» спином. Поскольку направление вылета такого электрона не определено,

то и импульс его также не определён. Следовательно, ему соответствует локализованное

состояние. Вклад одного такого акта рассеяния в общую плотность состояний ничтожно

мал, однако, когда концентрация примеси становится достаточно большой (сравнимой с

общей концентрацией атомов в кристалле),

это приводит к формированию зоны

локализованных состояний непосредственно на уровне Ферми, как это показано на

Рис.8.3.

Поскольку дополнительные состояния возникают непосредственно на уровне

Ферми, то в них попадают электроны, определяющие явления переноса. Ясно, что эффект

может наблюдаться только в том случае, если размытие уровня Ферми, которое

составляет ~ kT оказывается меньше ширины Кондо

-пика (по имени исследователей,

153

описавших возникновение таких состояний, его ещё называют резонансом Абрикосова-

Сула - РАС). Следовательно, РАС наблюдается только ниже некой характерной

температуры, называемой температурой Кондо – T

Кондо

. С параметрами ВСС – состояний

Кондо

связана следующим образом:

ГU

UEE

Кондо

eГUТ

)(

(11.3)

где U – кулоновское отталкивание между двумя электронами, локализованными

на примеси одновременно.

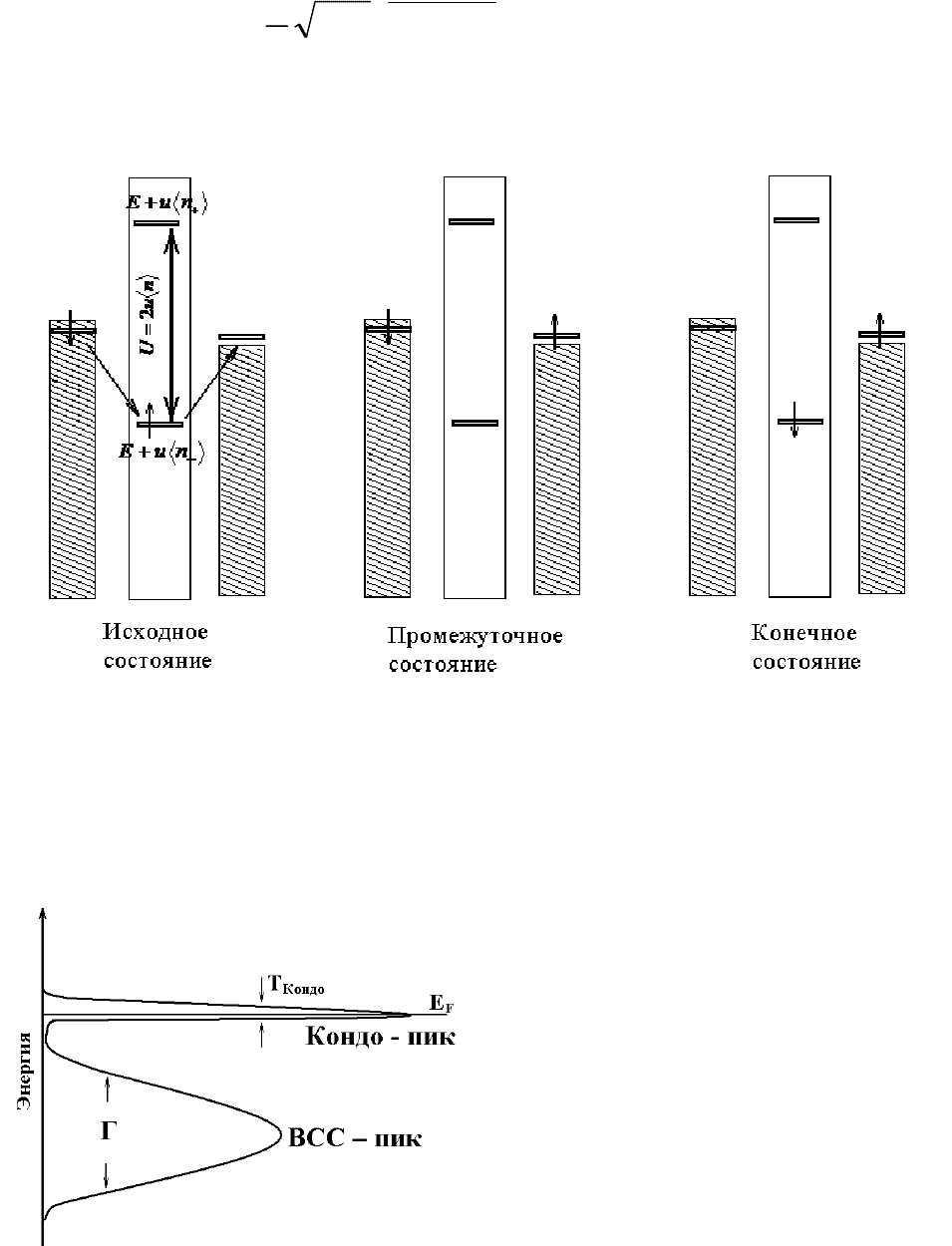
Рис. 7.3. Схема рассеяния электронов проводимости на «шубе» спиново-

поляризованных ВСС – электронов. Заштрихованные столбики обозначают состояния

зоны проводимости, белые – положение ВСС. Электрон со спином «вниз» выбивает

электрон со спином «вверх» и занимает его место в ВСС - «шубе». Экспериментально

наблюдаемым итогом является переворот спина электрона проводимости и примеси. В

случае рассеяния электрона со

спином «вверх» всё остаётся без изменений.

Рис. 8.3. Процесс рассеяния с

переворотом спина, показанный

схематически на Рис. 7.3., приводит к

формированию на уровне Ферми

дополнительного пика плотности

состояний (Кондо – пик или РАС).

154

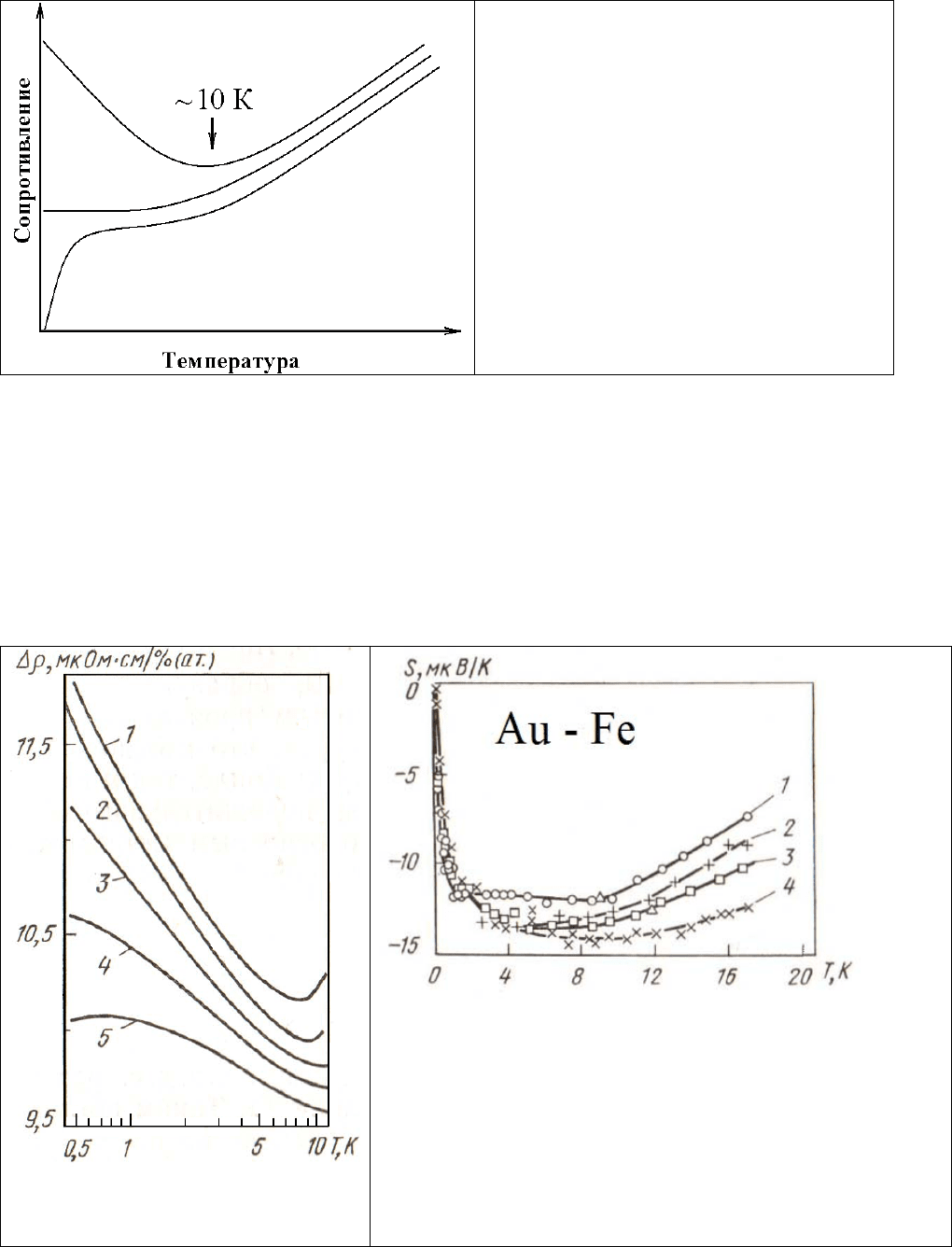
Рис.9.3. Возможные температурные

зависимости сопротивления металлов

при охлаждении.

Нижняя кривая: металл может перейти

в сверхпроводящее состояние.

Средняя кривая: сопротивление

становится постоянным из-з

доминирования рассеяния на

нейтральных примесях.

Верхняя кривая: доминирование Кондо-

рассеяния на увеличивающихся по мере

охлаждения ВСС – «шубах» приводит к

неограниченному росту сопротивления.

Поскольку ясно, что при охлаждении ВСС – «шубы» становятся всё больше, то,

очевидно, что и Кондо – рассеяние должно усиливаться по мере охлаждения ниже Т

кондо

Это обстоятельство позволило объяснить тот факт, что во многих металлах при низких

температурах наблюдается рост сопротивления при охлаждении, Рис. 9.3. Этот результат

казался совершенно загадочным, поскольку вымораживание фононов должно приводить,

да и приводит, к уменьшению сопротивления с охлаждением, Рис.10.3. До Кондо

механизм, способный обеспечить обратное был неизвестен.

Рис. 10.3. Температурные зависимости сопротивления

(слева) и термоЭДС (вверху) сплавов золота,

легированных примесью железа. Содержание железа

растёт от 0,0025 ат.% - кривая 1, до 0, 02 ат.% (кривая

4) и 0,025 ( кривая 5). Уменьшение сопротивления связано

с ослаблением рассеяния на фононах, а рост

сопротивления и термоЭДС связан с формированием

РАС и его усилением при дальнейшем охлаждении. Т

Кондо

составляет ~ 10 К.

155

Итак, электроны, входящие в состав РАС обладают спинами, направленными

противоположно спину инициировавшей их локализацию примеси. При Т < Т

Кондо

ширина

РАС меньше kT и, следовательно, электроны достаточно «усидчивы». Это означает, что

наблюдаемый магнитный момент примеси должен быть уменьшен на величину

суммарного магнитного момента электронов РАС. Вплоть до полной компенсации

момента примеси. В последнем случае примесь оказывается нейтральной (из-за ВСС -

экранировки) и немагнитной (из-за РАС – компенсации магнитного момента). Рассеяние

электронов на такой примеси не зависит от температуры и сопротивление в пределе

низких температур стремится к постоянной величине. Если бы это было не так, то в

пределе низких температур металлическое состояние металла с магнитной примесью было

бы невозможно (верхняя кривая на Рис. 9.3.).

Конкурирующим взаимодействием с эффектом Кондо является РККИ –

взаимодействие (РККИ

– Рудерман-Киттель-Касуйа-Иосида – сокращение от фамилий

авторов, описавших этот механизм). Оно заключается в том, что у электронов,

компенсирующих момент примеси есть свои, следующие от примеси, соседи. И если

устойчива антиферромагнитная ориентация моментов, то момент следующих соседей

должен быть ориентирован так же как у примеси и обратно спину электронов «шубы».

А у

этих соседей есть свои соседи и так далее. Результатом всего этого является

возникновение осцилляций ориентаций спина электронов проводимости, показанные на

Рис. 11.3. Повышение температуры приводит к размыванию осцилляций, а охлаждение,

напротив, делает их более устойчивыми. Следовательно, охлаждение должно приводить к

увеличению эффективного радиуса устойчивости РККИ-осцилляций. Перекрытие хвостов

этих осцилляций

приводит к возникновению взаимодействия между магнитными

примесями и упорядочению магнитных моментов последних. Поскольку в такой ситуации

магнитный момент примеси более не может изменяться вследствие Кондо-рассеяния, то

возникновение магнитного взаимодействия в подсистеме примесей подавляет Кондо-

эффект.

Рис.11.3. Осцилляции спиновой поляризации электронов вокруг магнитной

примеси по модели РККИ.

156

Параметром, определяющим возникновение магнитного порядка является т.н.

температура РККИ, связанная следующим образом с величиной постоянной обменного

взаимодействия

J электронов проводимости с магнитным моментом примеси:

РККИ

(12.3)

W - плотность состояний зоны проводимости на уровне Ферми.

В свою очередь, величина

определяется степенью гибридизации ВСС-уровня с

состояниями зоны проводимости

, имеющими, как правило, s-природу и положения

ВСС-уровня относительно уровня Ферми:

−

(13.3)

Для Т

Кондо

справедливо следующая связь с магнитным взаимодействием

электронов проводимости с магнитной примесью:

Кондо

~exp

()

WE J

⎡

⎤

−

⎢

⎥

⎣

⎦

(14.3)

= - температура Ферми, а

- кратность вырождения магнитного уровня.

Из этих формул следует важный вывод: Т

РККИ

убывает с увеличением E

–

глубины залегания ВСС-уровня под уровнем Ферми, тогда как Т

Кондо

, напротив возрастает

(сравните формулы 11.3, 12.3 и 13.3). Это означает, что если для «победы» РККИ-

взаимодействия более благоприятна d-природа ВСС-состояний, то с точки зрения Кондо-

эффекта более предпочтительны глубоко лежащие f-состояния с большей энергией связи.

Другим фактором, определяющим относительную устойчивость магнитного порядка или

Кондо-эффекта является величина обменной константы

J . Действительно, её увеличение

вызывает экспоненциальный рост Т

Кондо

и только линейный рост Т

РККИ

. Это означает, что

возможна ситуация когда из-за сильного обменного взаимодействия электронов

проводимости с магнитной примесью даже большая концентрация последней не будет

приводить к формированию магнитного порядка, а напротив к установлению

немагнитного состояния с отсутствием магнитного момента даже у исходно магнитной

примеси.

157

Материалы такого рода принято называть концентрированными Кондо –

системами (ККС), а подсистему упорядоченной или неупорядоченной примеси -

немагнитной Кондо – решёткой (НКР).

Типичными примерами ККС могут служить следующие материалы: CeAl

CeCu

, CeCu

, UBe

, UPt

. У всех этих материалов ВСС создаётся за счёт 4f-состояний

лантаноидов и 5f-состояний урана. Заполнение РАС зависит от полного магнитного

момента примеси, который должен быть компенсирован электронами проводимости. При

T ~ 0 заполнение составляет

, т.е. для

=j РАС расположен точно на уровне

Ферми. В соединениях церия шестикратно вырожденный 4f-уровень церия расщепляется

кристаллическим полем на три дублета. Однако, поскольку Т

Кондо

много меньше величины

этого расщепления, то эффективно работает только нижний дублет, так что соединения

церия ведут себя как материалы с

=j , у которых РАС попадает точно на уровень

Ферми. Для этих соединений установлено увеличение плотности состояний на уровне

Ферми в 100 – 1000 раз, эквивалентное такому же увеличению эффективной массы

электронов проводимости.

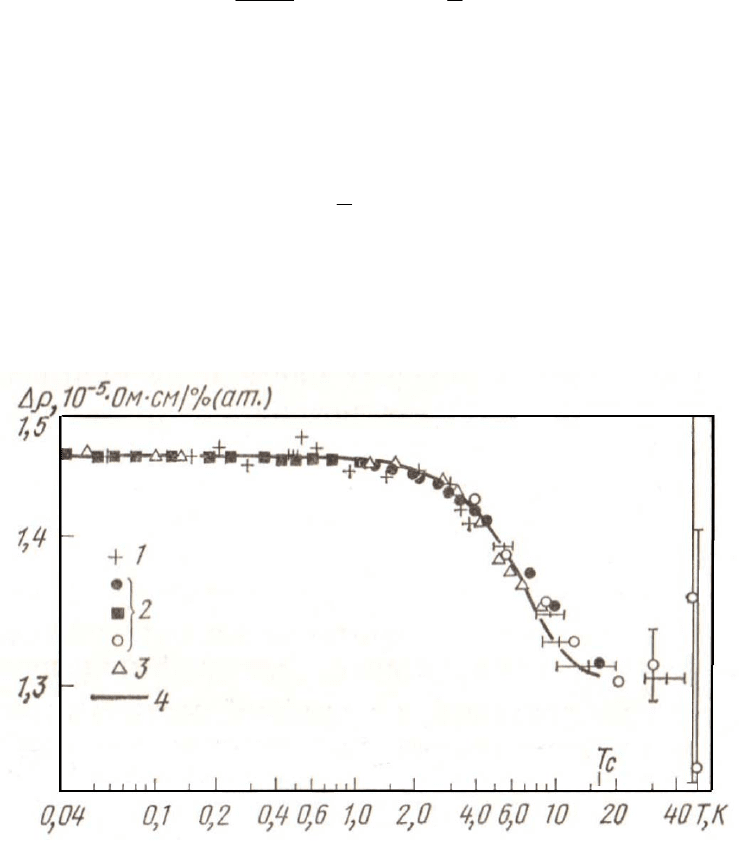
Рис. 12.3. Температурная зависимость сопротивления сплава Cu-Fe,

нормированная на концентрацию примеси железа [1]. Концентрация железа изменяется

в интервале от 6 10

-3

до 6 10

-2

ат.%. Значком Т

обозначена Т

Кондо

. Видно, что в

низкотемпературном пределе сопротивление становится независящим от температуры.

Очевидно, встаёт вопрос: но ведь и формирование «шубы» ВСС-электронов тоже

должно приводить к осцилляциям заряда вокруг примеси, чередующего отрицательно и

положительно заряженные области. А что тогда мешает перекрытию не только спиновых,

158

но и просто зарядовых осцилляций, типа тех, что показаны на Рис.2.3.? И что произойдёт

с электрическими свойствами материала, если такое перекрытие случится? Конечно,

пространственная граница ВСС – «шубы» определяется из условия:

kTE

(15.3)

где под

E понимается энергия взаимодействия электрона с ВСС-примесью в

самой внешней части «шубы». Понижая температуру можно добиться выполнения

условия (15.3) для всё большего количества оболочек, так что осцилляции, порождаемые

различными примесями будут всё протяжённее и, в конце концов, перекроются.

Действительно, такие образования известны под именем «Фриделевских осцилляций», по

имени А.Фриделя, предложившего

модель формирования ВСС-состояний.

Строгое рассмотрение перехода от случая малой концентрации примеси, когда

зарядовые осцилляции затухают до того как встретят друг друга к случаю когда это уже

не так является сложной задачей, уводящей в сторону от основной темы. Можно

порекомендовать обратиться к книге [5.4] (глава «Сильно легированные

полупроводники»). Качественно же дело

сводится к следующему. Выполнить условие

(15.3) можно либо увеличивая концентрацию примеси и уменьшая, тем самым, расстояние

на котором должны быть устойчивы зарядовые осцилляции либо понижая температуру и

увеличивая протяжённость последних. При перекрытии осцилляций электрон в данной

ВСС-«шубе» начинает чувствовать не только влияние «своей» примеси, но и тех, чьи

осцилляции перекрылись

с данной. Следовательно, электронная плотность становится

периодической волной, аналогично плотности электронов регулярной решётки. Это

соответствует формированию т.н. примесной зоны, аналогичной зонам основной решётки.

В этом случае примесь становится нейтральна, так же как и атомы основной решётки.

Рассеяние на нейтральной примеси приводит к сопротивлению, не зависящему от

температуры [5.4]. Действительно, такое поведение

наблюдается экспериментально, см.

Рис 12.3.

3.6. Кондо – решётки

В случае, когда ВСС-состояния образованы d-состояниями примеси,

протяжённость этих орбиталей относительно велика и увеличение концентрации примеси

неизбежно приводит к магнитному порядку вследствие прямого или косвенного

перекрытия d-орбиталей. Если же ВСС-примесь образована f-металлом, то даже в случае,

если такая примесь занимает соседние узлы решётки, перекрытия не наблюдается. Это

связано с

малостью радиуса f-орбиталей, надёжно упакованных под внешними s-, p- и d-