Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

2.8 Exercises 61

27. Apply v =lnu and then v (x, y)=f (x)+g (y) to solve the following

equations:

(a) x

+ y

= u

(b) x

+ y

=(xyu)

28. Apply

√

u = v and v (x, y)=f (x)+g (y) to solve the equation

+ y

=4u.

29. Using v =lnu and v = f (x)+g (y), show that the solution of the

Cauchy problem

+ x

=(xyu)

,u(x, 0) = e

u (x , y)=exp



+ i

√



30. Reduce each of the following equations into canonical form and ﬁnd th e

general solution:

(a) u

+ u

= u,(b)u

+ xu

= y,

+2xy u

= x,(d)u

− yu

− u =1.

31. Find the solution of each of the following equations by the method of

separation of variables:

(a) u

− u

=0, u (0,y)=2e

(b) u

− u

= u, u (x, 0) = 4e

−3x

+ bu

=0, u (x, 0) = αe

βx

where a, b, α and β are constants.

32. Find the solution of the following initial-value systems

(a) u

+3uu

= v − x, v

− cv

=0withu (x, 0) = x and v (x, 0) = x.

(b) u

+2uu

= v − x, v

− cv

=0withu (x, 0) = x and v (x, 0) = x.

62 2 First-Order, Quasi-Linear Equations and Method of Characteristics

33. Solve the following initial-value systems

(a) u

+ uu

= e

−x

v, v

− av

=0withu (x, 0) = x and v (x, 0) = e

(b) u

− 2uu

= v − x, v

+ cv

=0withu (x, 0) = x and v (x, 0) = x.

34. Consider th e Fokker–Planck equation (See Reif (1965)) in statistical me-

chanics to describe the evolution of the probability distribution function

in the form

= u

+(xu)

u (x , 0) = f (x) .

Neglecting the term u

, solve the ﬁrst-order linear equation

− xu

= u with u (x, 0) = f (x) .

Mathematical Models

“Physics can’t exist without mathematics which provides it with the only

language in which it can speak. Thus, services are continuously exchanged

between pure mathematical analysis and phy sics. It is really remarkable

that among works of analysis most useful for physics were those cultivated

for their own b eauty. In exchange, physics, exposing new problems, is as

useful for mathematics as it is a model for an artist.”

Henri Poincar´e

“It is no paradox to say in our most theoretical mod els we may be nearest

to our most practical applications.”

A. N. Whitehead

“... builds models based on data from all levels: gene expression, protein

location in the cell, models of cell function, and computer representations

of organs and organisms.”

E. Pennisi

3.1 Classical Equations

Partial diﬀerential equations arise frequently in formulating fundamental

laws of nature and in the study of a wide variety of physical, chemical,

and biological models. We start with a special type of second-order linear

partial diﬀerential equation for the following reasons. First, second-order

linear equations arise more frequently in a wide variety of applications.

Second, their mathematical treatment is simpler and easier to understand

than that of ﬁrst-order equations in general. Usually, in almost all physical

64 3 Mathematical Models

phenomena (or physical processes), the dependent variable u = u (x, y, z, t)

is a function of three space variables, x, y, z and time variable t.

The three basic types of second-order partial diﬀerential equations are:

(a) The wave equation

− c

+ u

)=0. (3.1.1)

(b) The heat equation

− k (u

+ u

)=0. (3.1.2)

+ u

=0. (3.1.3)

In this section, we list a few more common linear partial diﬀerential equa-

tions of importance in applied mathematics, mathematical physics, and en-

gineering science. Such a list naturally cannot ever be complete. Included

are only equations of most common interest:

(d) The Poisson equation

∇

u = f (x, y, z) . (3.1.4)

(e) The Helmholtz equation

∇

u + λu =0. (3.1.5)

(f) The biharmonic equation

∇

u = ∇



∇



=0. (3.1.6)

(g) The biharmonic wave equation

+ c

∇

u =0. (3.1.7)

(h) The telegraph equation

+ au

+ bu = c

. (3.1.8)

(i) The Schr¨odinger equations in quantum physics

iψ



−





∇

+ V (x, y, z)



ψ, (3.1.9)

∇

Ψ +



[E − V (x, y, z)] Ψ =0. (3.1.10)

(j) The Klein–Gordon equation

u + λ

u =0, (3.1.11)

3.2 The Vibrating String 65

where

∇

≡

∂

∂x

∂

∂y

∂

∂z

, (3.1.12)

is the Laplace operator in rectangular Cartesian coordinates (x, y, z),

 ≡∇

−

∂

∂t

, (3.1.13)

is the d’Alembertian, and in all equations λ, a, b, c, m, E are constants

and h =2π is the Planck constant.

(k) For a compressible ﬂuid ﬂow, Euler’s equations

+(u ·∇) u = −

∇p, ρ

+div(ρu)=0, (3.1.14)

where u =(u, v, w) is the ﬂuid velocity vector, ρ is the ﬂuid density,

and p = p (ρ) is the pressure that relates p and ρ (the constitutive

equation or equation of state).

Many problems in mathematical physics reduce to the solving of partial

diﬀerential equations, in particular, the partial diﬀerential equations listed

above. We will begin our study of these equations by ﬁrst examining in

detail the mathematical models representing physical problems.

3.2 The Vibrating String

One of the most important problems in mathematical physics is the vi-

bration of a stretched string. Simplicity and frequent occurrence in many

branches of mathematical physics make it a classic example i n the theory

of partial diﬀerential equations.

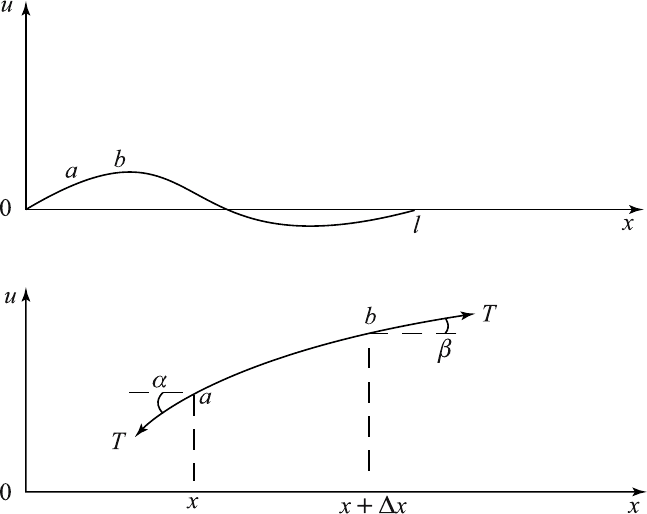
Let us consider a stretched string of length l ﬁxed at the end points. The

problem here is to determine the equation of motion which characterizes

the position u (x, t) of the string at time t after an initial disturbance is

given.

In or der to obtain a simple equation, we make the following assumptions:

1. The string is ﬂexible and elastic, that is the string cannot resist bending

moment and thus the tension in the string is always in the direction of

the tangent to the existing proﬁle of the string.

2. There is no elongation of a single segment of the string and hence, by

Hooke’s law, the tension is constant.

3. The weight of the string is small compared with the tension in the

string.

4. The deﬂection is small compared with the length of the string.

5. The slope of the displaced string at any point is small compared with

unity.

66 3 Mathematical Models

6. There is only pure transverse vibration.

We consider a diﬀerential element of the stri ng. Let T be the tension at the

end points as shown in Figure 3.2.1. The forces acting on the element of

the string in the vertical direction are

T sin β − T sin α.

By Newton’s second law of motion, the resultant force is equal to the

mass times the acceleration. Hence,

T sin β − T sin α = ρδsu

(3.2.1)

where ρ is the line density and δs is the smaller arc length of the string.

Since the slope of the displaced string is small, we have

δs ≃ δx.

Since the angles α and β are small

sin α ≃ tan α, sin β ≃ tan β.

Figure 3.2.1 An Element of a vertically displaced string.

3.3 The Vibrating Membrane 67

Thus, equation (3.2.1) becomes

tan β − tan α =

ρδx

. (3.2.2)

But, from calculus we know that tan α and tan β are the slopes of the string

at x and x + δx:

tan α = u

(x, t)

and

tan β = u

(x + δx, t)

at time t. Equation (3.2.2) may thus be written as

δx

)

x+δx

− (u

)

δx

(x + δx, t) − u

(x, t)] =

In the limit as δx approaches zero, we ﬁnd

= c

(3.2.3)

where c

= T/ρ.Thisiscalledtheone-dimensional wave equation.

If there is an external force f per unit length acting on the string.

Equation (3.2.3) assumes the form

= c

+ F, F = f/ρ, (3.2.4)

where f may be pressure, gravitation, resistance, and so on.

3.3 The Vibrating Membrane

The equation of the vibrating membrane o ccurs in a large number of prob-

lems in applied mathematics and mathematical p hysics. Before we derive

the equation for the vibrating membrane we make certain simplif ying as-

sumptions as in the case of the vibrating string:

1. The membrane is ﬂexible and elastic, that is, the membrane cannot

resist bending moment an d the tension in the membrane is always in

the direction of the tangent to the existing proﬁle of the membrane.

2. There is no elongation of a single segment of the membrane and hence,

by Hooke’s law, the tension is constant.

3. The weight of the membrane is small compared with the tension in the

membrane.

4. The deﬂection is small compared with the minimal diameter of the

membrane.

68 3 Mathematical Models

5. The slope of the displayed membrane at any point is small compared

with unity.

6. There is only pure transverse vibration.

We consider a small element of the membrane. Since the deﬂection and

slope are small, the area of the element is approximately equal to δxδy.If

T is the tensile force per unit length, then the forces acting on the sides of

the element are Tδxand Tδy, as shown in Figure 3.3.1.

The forces acting on the element of the membrane in the vertical direc-

tion are

Tδxsin β − Tδxsin α + Tδysin δ − Tδysin γ.

Since the slopes are small, sines of the angles are approximately equal to

their tangents. Thus, the resultant force becomes

Tδx(tan β − tan α)+Tδy(tan δ − tan γ) .

By Newton’s second law of motion, the resultant force is equal to the

mass times the acceleration. Hence,

Tδx(tan β − tan α)+Tδy(tan δ − tan γ)=ρδAu

(3.3.1)

where ρ is the mass per unit area, δA ≃ δxδy istheareaofthiselement,

and u

is computed at some point in the region under consideration. But

from calculus, we have

Figure 3.3.1 An element of vertically displaced membrane.

3.4 Waves in an Elastic Medium 69

tan α = u

,y)

tan β = u

,y+ δy)

tan γ = u

(x, y

)

tan δ = u

(x + δx, y

)

where x

and x

are the values of x between x and x+δx,andy

and y

are

the valu es of y between y and y + δy. Substitu ting these values in (3.3.1),

we obtain

Tδx[u

,y+ δy) − u

,y)] + Tδy[u

(x + δx, y

) − u

(x, y

)]

= ρδxδyu

Division by ρδxδy yields



,y+ δy) − u

,y)

δy

(x + δx, y

) − u

(x, y

)

δx



= u

(3.3.2)

In the limit as δx approaches zero and δy approaches zero, we ob tain

= c

+ u

) , (3.3.3)

where c

= T/ρ. This equation is called the two-dimensional wave equation.

If there is an external force f per unit area acting on the membrane.

Equation (3.3.3) takes the form

= c

+ u

)+F, (3.3.4)

where F = f/ρ.

3.4 Waves in an Elastic Medium

If a small disturbance is originated at a point in an elastic medium, neigh-

boring particles are set into motion, and the medium is put under a state

of strain. We consider such states of motion to extend in all directions. We

assume that the displacements of the medium are small and that we are

not concerned with translation or rotation of the medium as a whole.

Let the body under investigation be homogeneous and isotropic. Let δV

be a diﬀerential volume of the body, and let the stresses acting on the faces

of the volume be τ

, τ

. The ﬁrst three

stresses are called the normal stresses and the rest are called the shear

stresses. (See Figure 3.4.1).

We shall assume that the stress tensor τ

is symmetric describing the

condition of the rotational equilibrium of the volume element, that is,

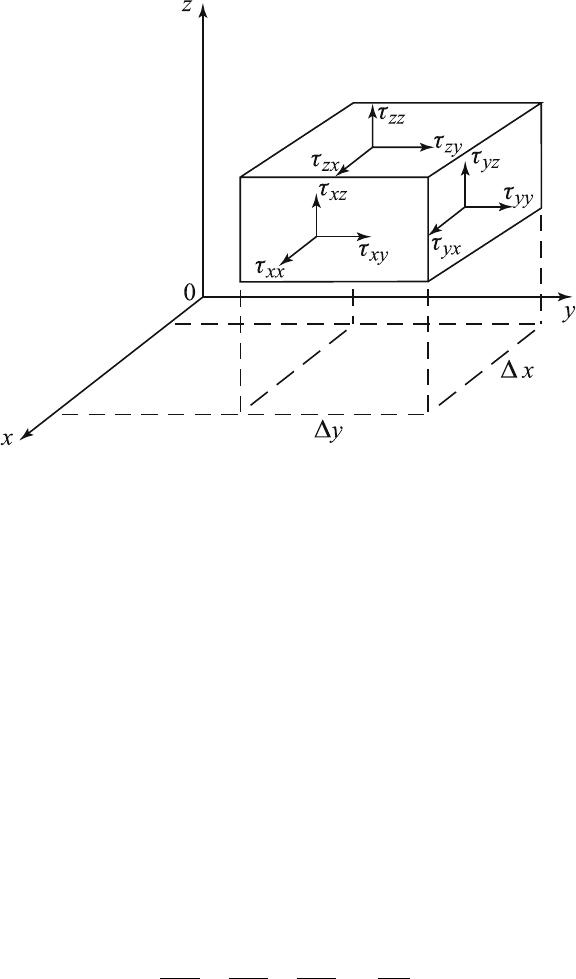
70 3 Mathematical Models

Figure 3.4.1 Volume element of an elastic body.

= τ

,i= j, i, j = x , y, z. (3.4.1)

Neglecting the body forces, the sum of all the forces acting on th e volume

element in the x-direction is

(τ

)

x+δx

− (τ

)

δyδz +

(τ

)

y +δy

− (τ

)

δzδx

(τ

)

z+δz

− (τ

)

δxδy.

By Newton’s l aw of motion this resultant force is equal to the mass times

the acceleration. Thus, we obtain

(τ

)

x+δx

− (τ

)

δyδz +

(τ

)

y +δy

− (τ

)

δzδx

(τ

)

z+δz

− (τ

)

δxδy = ρδxδyδzu

(3.4.2)

where ρ is the density of the b ody and u is the displacement component in

the x-direction. Hence, in the limit as δV approaches zero, we obtain

∂τ

∂x

∂τ

∂y

∂τ

∂z

= ρ

∂

∂t

. (3.4.3)

Similarly, the following two equations corresponding to y and z directions

are obtained: