Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

3.4 Waves in an Elastic Medium 71

∂τ

∂x

∂τ

∂y

∂τ

∂z

= ρ

∂

∂t

, (3.4.4)

∂τ

∂x

∂τ

∂y

∂τ

∂z

= ρ

∂

∂t

, (3.4.5)

where v and w are the displacement components in the y and z d irections

respectively.

We may now deﬁne linear strains [see Sokolnikoﬀ (1956)] as

∂u

∂x

,ε



∂w

∂y

∂v

∂z



∂v

∂y

,ε



∂u

∂z

∂w

∂x



, (3.4.6)

∂w

∂z

,ε



∂v

∂x

∂u

∂y



in which ε

, ε

represent unit elongations and ε

, ε

represent

unit shearing strains.

In the case of an isotropic body, generalized Hooke’s law takes the form

= λθ +2µε

,τ

=2µε

= λθ +2µε

,τ

=2µε

, (3.4.7)

= λθ +2µε

,τ

=2µε

where θ = ε

+ ε

is called the dilatation,andλ and µ are Lame’s

constants.

Expressing stresses in terms of displacements, we obtain

= λθ +2µ

∂u

∂x

= µ



∂v

∂x

∂u

∂y



, (3.4.8)

= µ



∂w

∂x

∂u

∂z



By diﬀerentiating equations (3.4.8), we obtai n

∂τ

∂x

= λ

∂θ

∂x

+2µ

∂

∂x

∂τ

∂y

= µ

∂

∂x∂y

+ µ

∂

∂y

, (3.4.9)

∂τ

∂z

= µ

∂

∂x∂z

+ µ

∂

∂z

Substituting equation (3.4.9) into equation (3.4.3) yields

72 3 Mathematical Models

∂θ

∂x

+ µ



∂

∂x

∂

∂x∂y

∂

∂x∂z



+ µ



∂

∂x

∂

∂y

∂

∂z



= ρ

∂

∂t

(3.4.10)

We note that

∂

∂x

∂

∂x∂y

∂

∂x∂z

∂

∂x



∂u

∂x

∂v

∂y

∂w

∂z



∂θ

∂x

and introduce the notation

△ = ∇

∂

∂x

∂

∂y

∂

∂z

The symbol △ or ∇

is called the Laplace operator. Hence, equation (3.4.10)

becomes

(λ + µ)

∂θ

∂x

+ µ∇

u = ρ

∂

∂t

. (3.4.11)

In a similar manner, we obtain the other two equations which are

(λ + µ)

∂θ

∂y

+ µ∇

v = ρ

∂

∂t

. (3.4.12)

(λ + µ)

∂θ

∂z

+ µ∇

w = ρ

∂

∂t

. (3.4.13)

The set of equations (3.4.11)–(3.4.13) is called the Navier equations of mo-

tion. In vector form, the Navier equations of motion assume the form

(λ + µ)grad divu + µ∇

u = ρ u

, (3.4.14)

where u = ui + vj + w k and θ =divu.

(i) If div u = 0, the general equation becomes

µ∇

u = ρ u

= c

∇

u, (3.4.15)

where c

is called the transverse wave velocity given by



µ/ρ.

This is the case of an equivoluminal wave propagation, since the volume

expansion θ is zero for waves moving with this velocity. Sometimes these

waves are called waves of distortion because the velocity of propagation

depends on µ and ρ; the shear modulus µ characterizes the distortion and

rotation of the volume element.

3.4 Waves in an Elastic Medium 73

(ii) When curl u = 0, the vector identity

curl curl u =graddivu −∇

gives

grad div u = ∇

Then the general equation becomes

(λ +2µ) ∇

u = ρ u

= c

∇

u, (3.4.16)

where c

is called the longitudinal wave velocity given by

λ +2µ

This is the case of irrotational or dilatational wave propagation, since

curl u = 0 describes irrotational motion. Equations (3.4.15) and (3.4.16)

are called the three-dimensional wave equations.

In general, the wave equation may be written as

= c

∇

u, (3.4.17)

where the Laplace operator may be one, two, or three dimensional. The

importance of the wave equation stems from the facts that this type of

equation arises in many physical problems; for example, sound waves in

space, electrical vibration in a conductor, torsional oscillation of a rod,

shallow water waves, linearized supersonic ﬂow in a gas, waves in an elec-

tric transmission line, waves in magnetohydrodynamics, and longitudinal

vibrations of a bar.

To give a more general method of decomposing elastic waves into trans-

verse and longitudinal wave forms, we write the Navier equations of motion

in the form

∇

u +



− c



grad (div u)=u

. (3.4.18)

We now decompose this equation into two vector equations by deﬁning

u = u

+ u

,whereu

and u

satisfy the equations

div u

= 0 and curl u

= 0. (3.4.19ab)

Since u

is deﬁned by (3.4.19a) that is divergenceless, it follows from vector

analysis that there exists a rotation vector ψ

ψ such that

74 3 Mathematical Models

=curlψ

ψ, (3.4.20)

where ψ

ψ is called the vector potential.

On the other hand, u

is irrotational as given by (3.4. 19b), so there

exists a scalar function φ (x,t), called th e scalar potential such that

=gradφ. (3.4.21)

Using (3.4.20) and (3.4.21), we can write

u =curlψ

ψ +gradφ. (3.4.22)

This means that the displacement vector ﬁeld is decomposed into a diver-

genceless vector and irrotati onal vector.

Inserting u = u

+ u

into (3.4.18), taking the divergence of each term

of the resulting equation, and then using (3.4.19a) gives

div

∇

− (u

)

=0. (3.4.23)

It is noted that the curl of the square bracket in (3.4.23) is also zero.

Clearly, any vector whose divergence and curl both vanish is identically a

zero vector. Consequently,

∇

=(u

)

. (3.4.24)

This shows that u

satisﬁes the vector wave equation with the wave velocity

.Sinceu

=gradφ, it is clear that the scalar potential φ also satisﬁes the

wave equation with the same wave speed. All solutions of (3.4.24) represent

longitudinal waves that are irrotational (since ψ

ψ = 0).

Similarly, we substitute u = u

+ u

into (3.4.18), take the curl of the

resulting equation, and use the fact that cur l u

= 0 to obtain

curl

∇

− (u

)

= 0. (3.4.25)

Since the di vergence of the expression inside the square bracket is also zero,

it follows that

∇

=(u

)

. (3.4.26)

This is a vector wave equation for u

whose solutions represent transverse

waves that are irrotational but are accompanied by no change in volume

(equivoluminal, transverse, rotational waves). These waves propagate with

awavevelocityc

We close this section by seeking time-harmonic solutions of (3.4.18) in

the form

u =Re

U (x, y, z) e

iω t

. (3.4.27)

3.5 Conduction of Heat in Solids 75

Invoking (3.4.27) into equation (3.4.18) gives the following equation for

the function U

∇

U +(c

− c

)grad(div U)+ω

U =0. (3.4.28)

Inserting, u = u

+ u

, and using the above method of taking the

divergence and curl of (3.4.28) respectively leads to equation for U

and

as follows

∇

+ k

∇

=0, ∇

+ k

=0, (3.4.29)

where

and k

. (3.4.30)

Equations (3.4.29) are called the reduced wave equations (or the Helmholtz

equations)forU

and U

. Obviously, equations (3.4.29) can also be de-

rived by assuming time-harmonic solutions for u

and u

in the form

⎛

⎝

⎞

⎠

= e

iω t

⎛

⎝

⎞

⎠

, (3.4.31)

and substituting these results into (3.4.24) and (3.4.26) respectively.

3.5 Conduction of Heat in Solids

We consider a domain D

∗

bounded by a closed surface B

∗

.Letu (x, y, z, t)

be the temperature at a point (x, y, z)attimet. If the temperature is not

constant, heat ﬂows from places of higher temperature to places of lower

temperature. Fourier’s law states that the rate of ﬂow is proportional to

the gradient of the temperature. Thus the velocity of the heat ﬂow in an

isotropic body is

v = −Kgradu, (3.5.1)

where K is a constant, called the thermal conductivity of the body.

Let D be an arbitr ary domain bounded by a closed surface B in D

∗

Then the amount of heat leaving D per unit time is



ds,

where v

= v · n is the component of v in the direction of the outer un it

normal n of B. Thus, by Gauss’ theorem (Divergence theorem)

76 3 Mathematical Models



ds =



div (−Kgradu) dx dy dz

= −K



∇

udxdydz. (3.5.2)

But the amount of heat in D is given by



σρu dxdy dz, (3.5.3)

where ρ is the density of the material of the body and σ is its speciﬁc heat.

Assuming that integration and diﬀerentiation are interchangeable, the rate

of decrease of heat in D is

−



σρ

∂u

∂t

dx dy dz. (3.5.4)

Since the rate of decrease of heat in D must be equal to the amount of heat

leaving D per unit time, we have

−



σρu

dx dy dz = −K



∇

udxdydz,

−



σρu

− K∇

dx dy dz =0, (3.5.5)

for an arbitrary D in D

∗

. We assume that the integrand is continuous. If we

suppose that the integrand is not zero at a point (x

)inD, then, by

continuity, the integrand is not zero in a small region surrounding the point

). Continuing in this fashion we extend the region encompassing

D. Hence th e integral must be nonzero. This contradicts (3.5.5). Thus, the

integrand is zero everywhere, that is,

= κ∇

u, (3.5.6)

where κ = K/σρ. This is kn own as the heat equation.

This type of equation appears in a great variety of problems in math-

ematical physics, for example the concentration of diﬀusing material, the

motion of a t idal wave in a long channel, transmission in electrical cables,

and unsteady boundary layers in viscous ﬂuid ﬂows.

3.6 The Gravitational Potential

In this section, we shall derive one of the most well-known equations in the

theory of partial diﬀerential equations, the Laplace equation.

3.6 The Gravitational Potential 77

Figure 3.6.1 Two particles at P and Q.

We consider two particles of masses m and M,atP and Q as shown

in Figure 3.6.1. Let r be the distance between them. Then, according to

Newton’s law of gravitation, a force proportional to the product of their

masses, and inversely proportional to the square of th e distance between

them, is given in the form

F = G

, (3.6.1)

where G is the gravitational constant.

It is customary in potential theory to choose the unit of force so that

G =1.Thus,F becomes

F =

. (3.6.2)

If r represents the vector PQ, the force per unit mass at Q due to the mass

at P may be written as

F =

−mr

= ∇





, (3.6.3)

which is called the intensity of the gravitational ﬁeld of force.

We supp ose that a particle of unit mass moves under the attraction of

the particle of mass m at P from inﬁnity up to Q. The work done by the

force F is

78 3 Mathematical Models



∞

Fdr =



∞

∇





dr =

. (3.6.4)

This is called the potential at Q due to the particle at P . We denote this

V = −

, (3.6.5)

so that the intensity of force at P is

F = ∇





= −∇V. (3.6.6)

We shall now consider a number of masses m

, m

, ..., m

,whose

distances from Q are r

, r

, ..., r

, respectively. Then the force of attraction

per unit mass at Q due to the system is

F =



k=1

∇

= ∇



k=1

. (3.6.7)

The work done by the forces acting on a particle of unit mass is



∞

F · dr =



k=1

= −V. (3.6.8)

Then the potential satisﬁes the equation

∇

V = −∇



k=1

= −



k=1

∇





=0,r

=0. (3.6.9)

In the case of a continuous distribution of mass in some volume R,wehave,

as in Figure 3.6.2.

V (x, y, z)=



ρ (ξ, η,ζ)

dR, (3.6.10)

where r =

(x − ξ)

+(y − η)

+(z − ζ)

and Q is outside the body. It

immediately follows that

∇

V =0. (3.6.11)

This equation is called the Laplace equation, also known as the potential

equation. It appears in many physical problems, such as those of electro-

static potentials, potentials in hydrodynamics, and harmonic potentials in

the theory of elasticity. We observe that the Laplace equation can be viewed

as the special case of the heat and the wave equations when the dependent

variables involved are independent of time.

3.7 Conservation Laws and The Burgers Equation 79

Figure 3.6.2 Continuous Mass Distribution.

3.7 Conservation Laws and The Burgers Equat io n

A conservation law states that the rate of change of the total amount of

material contained in a ﬁxed domain of volume V is equal to the ﬂux of

that material across the closed bounding surface S of the domain. If we

denote the density of the material by ρ (x,t) and the ﬂux vector by q (x,t),

then the conservation law is given by



ρdV = −



(q · n) dS, (3.7.1)

where dV is the volume element and dS is the surface element of the bound-

ary surface S, n denotes the outward unit normal vector to S as shown in

Figure 3.7.1, and the right-hand side measures the outward ﬂu x — hence,

the minus sign is used.

Applying the Gauss divergence theorem and taking

inside the integral

sign, we obtain





∂ρ

∂t

+divq



dV =0. (3.7.2)

This result is true for any arbitrary volume V , and, if the integrand is

continuous, it must vanish everywhere in the domain. Thus, we obtain the

diﬀerential form of the conservation law

+divq =0. (3.7.3)

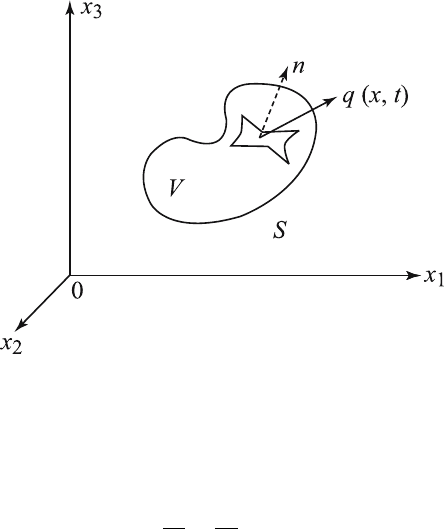
80 3 Mathematical Models

Figure 3.7.1 Volume V of a closed domain bounded by a surface S with surface

element d S and outward normal vector n.

The one-dimensional version of the conservation law (3.7.3) is

∂ρ

∂t

∂q

∂x

=0. (3.7.4)

To investigate the nature of the discontinuous solution or shock waves,

we assume a functional relation q = Q (ρ) and allow a jump discontinuity

for ρ and q. In many physical problems of interest, it would be a better

approximation to assume that q is a function of the density gradient ρ

well as ρ. A simple model is to take

q = Q (ρ) − νρ

, (3.7.5)

where ν is a positive constant. Substituting (3.7.5) into (3.7.4), we obtain

the nonlinear diﬀusion equation

+ c (ρ) ρ

= νρ

, (3.7.6)

where c (ρ)=Q

′

(ρ).

We multiply (3.7.6) by c

′

(ρ) to obtain

+ cc

= νc

′

(ρ) ρ

= ν

− c

′′

(ρ) ρ

. (3.7.7)

If Q (ρ) is a quadratic function in ρ,thenc (ρ) is linear in ρ,andc

′′

(ρ)=0.

Consequently, (3.7.7) becomes

+ cc

= νc

. (3.7.8)