Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

2.5 Method of Characteristics and General Solutions 41

Clearly, it follows by subtracting that

x − y =(z − y)

∂z

∂ζ

,x− z =(y − z)

∂y

∂ζ

Using the values for

∂x

∂ζ

∂z

∂ζ

,and

∂y

∂ζ

in (2.5.35), we obtain

(z − y)

∂u

∂ζ

=(y − z)

∂u

∂x

+(z − x)

∂u

∂y

+(x − y)

∂u

∂z

. (2.5.36)

If u = u (ξ, η) satisﬁes (2.5.31), then

∂u

∂ζ

= 0 and, hence, (2.5.36) reduces

to (2.5.31). This shows that the general solution (2.5.32) satisﬁes equation

(2.5.31).

Example 2.5.5. Find the solution of the equation

u (x + y) u

+ u (x − y) u

= x

+ y

, (2.5.37)

with the Cauchy data u =0ony =2x.

The characteristic equations are

u (x + y)

u (x − y)

+ y

ydx + xdy − udu

xdx − ydy − udu

Consequently,



xy −



= 0 and d





− y

− u





=0. (2.5.38)

These give two integrals

− x

+ y

= C

and 2xy − u

= C

, (2.5.39)

where C

and C

are constants. Hence, the general solution is



− y

− u

, 2xy − u



=0,

where f is an arbitrary function.

Using the Cauchy data in (2.5.39), we obtain 4C

=3C

. Therefore



− x

+ y





2xy − u



Thus, the solution of equation (2.5.37) is given by

=6xy +4



− y



. (2.5.40)

Example 2.5.6. Obtain the solution of the linear equation

− u

=1, (2.5.41)

42 2 First-Order, Quasi-Linear Equations and Method of Characteristics

with the Cauchy data

u (x , 0) = x

The characteristic equations are

−1

. (2.5.42)

Obviously,

= −1and

=1.

Clearly,

x + y = constant = C

and u − x = constant = C

Thus, the general solution is given by

u − x = f (x + y) , (2.5.43)

where f is an arbitrary function.

We now use the Cauchy data to ﬁnd f (x)=x

− x, and hence, the

solution is

u (x , y)=(x + y)

− y. (2.5.44)

The characteristics x + y = C

are drawn in Figure 2.5.1. The value of u

must be given at one point on each characteristic which intersects the line

y = 0 only at one point, as shown in Figure 2.5.1.

Figure 2.5.1 Characteristics of equation (2.5.41).

2.5 Method of Characteristics and General Solutions 43

Example 2.5.7. Obtain the solution of the equation

(y − u) u

+(u − x) u

= x − y, (2.5.45)

with the condition u =0onxy =1.

The characteristic equations for equation (2.5.45) are

y − u

u − x

x − y

. (2.5.46)

The parametric forms of these equations are

= y − u,

= u − x,

= x − y.

These lead to the following equations:

˙x +˙y +˙u = 0 and x ˙x + y ˙y + u ˙u =0, (2.5.47)

where the dot denotes the derivative with respect to t.

Integrating (2.5.47), we obtain

x + y + u =const.=C

and x

+ y

+ u

=const.=C

. (2.5.48)

These equations represent circles.

Using the Cauchy data, we ﬁnd that

=(x + y)

= x

+ y

+2xy = C

+2.

Thus, the integral surface is described by

(x + y + u)

= x

+ y

+ u

+2.

Hence, the solution is given by

u (x , y)=

1 − xy

x + y

. (2.5.49)

Example 2.5.8. Solve the linear equation

+ xu

= u, (2.5.50)

with the Cauchy data

u (x , 0) = x

and u (0,y)=y

. (2.5.51)

The characteristic equations are

44 2 First-Order, Quasi-Linear Equations and Method of Characteristics

dx − dy

y − x

dx + dy

y + x

Solving these equations, we obtain

u =

x − y

= C

(x + y)

u = C

(x + y) ,x

− y

= constant = C.

So the characteristics are rectangular hyperbolas for C>0orC<0.

Thus, the general solution is given by



x + y

− y



or, equivalently,

u (x , y)=(x + y) g



− y



. (2.5.52)

Using the Cauchy data, we ﬁnd that g





= x

,thatis,g (x)=x.

Consequently, the solu tion becomes

u (x , y)=(x + y)



− y



on x

− y

= C>0.

Similarly,

u (x , y)=(x + y)



− x



on y

− x

= C>0.

It follows from these results that u → 0 i n all regions, as x →±y

(or y →±x), and hence, u is continuous across y = ±x which represent

asymptotes of the rectangular hyperbolas x

− y

= C. However, u

and

are not continuous, as y →±x.Forx

− y

= C>0,

=3x

+2xy − y

=(x + y)(3x − y) → 0, as y →−x.

= −3y

− 2xy + x

=(x + y)(x − 3y) → 0, as y →−x.

Hence, both u

and u

are continuous as y →−x. On the other hand,

→ 4x

→−4x

as y → x.

This implies that u

and u

are discontinuous across y = x.

Combining all these results, we conclude that u (x, y) is continuous ev-

erywhere in the (x, t)-plane, and u

, u

are continu ous everywhere in the

(x, t)-plane except on the line y = x. Hence, the partial derivatives u

, u

are discontinuous on y = x. Thus, the development of discontinuities across

characteristics is a signiﬁcant feature of the solutions of partial diﬀerential

equations.

2.5 Method of Characteristics and General Solutions 45

Example 2.5.9. Determine the integral surfaces of the equation



+ u



− y



+ u





− y



u, (2.5.53)

with the data

x + y =0,u=1.

The characteristic equations are

x (y

+ u)

−y (x

+ u)

− y

) u

(2.5.54)

+ u)

−(x

+ u)

− y

)

Consequently,

log (xyu)=logC

xyu = C

From (2.5.54), we obtai n

xdx

+ u)

ydy

−y

+ u)

− y

) u

xdx + ydy − du

whence we ﬁnd that

+ y

− 2u = C

Using the given data, we obtain

= −x

and C

=2x

− 2,

so that

= −2(C

+1).

Thus the integral surface is given by

+ y

− 2u = −2 − 2xyu

2xyu + x

+ y

− 2u +2=0. (2.5.55)

46 2 First-Order, Quasi-Linear Equations and Method of Characteristics

Example 2.5.10. Obtain the solution of the equation

+ yu

= x exp (−u) (2.5.56)

with the data

u =0 on y = x

The characteristic equations are

x exp (−u)

(2.5.57)

= C

We also obtain from (2.5.57) that dx = e

du which can be integrated to

ﬁnd

= x + C

Thus, the general solution is given by



− x,



or, equivalently,

= x + g





. (2.5.58)

Applying the Cauchy data, we obtain g (x)=1− x. Thus, the solution of

(2.5.56) is given by

= x +1−

u =log



x +1−



. (2.5.59)

Example 2.5.11. Solve the initial-value problem

+ uu

= x, u (x, 0) = f (x) , (2.5.60)

where (a) f (x) = 1 and (b) f (x)=x.

The characteristic equations are

d (x + u)

x + u

. (2.5.61)

2.5 Method of Characteristics and General Solutions 47

Integration gives

t = log (x + u) − log C

(u + x) e

−t

= C

Similarly, we get

− x

= C

For case (a), we obtain

1+x = C

and 1 − x

= C

, and hence C

=2C

− C

Thus,



− x



=2(u + x) e

−t

− (u + x)

−2t

u − x =2e

−t

− (u + x) e

−2t

A simple manipulation gives th e solution

u (x , t)=x tanh t + sech t. (2.5.62)

Case (b) is left to the reader as an exercise.

Example 2.5.12. Find the integral surface of the equation

+ u

=1, (2.5.63)

so that the surf ace passes through an initial curve represented parametri-

cally by

x = x

(s) ,y= y

(s) ,u= u

(s) , (2.5.64)

where s is a parameter.

The characteristic equations for the given equations are

which are, in the parametric form,

dτ

= u,

dτ

=1,

dτ

=1, (2.5.65)

48 2 First-Order, Quasi-Linear Equations and Method of Characteristics

where τ is a parameter. Thus the solutions of this parametric system in

general depend on two parameters s and τ. We solve this system (2.5.65)

with the initial data

x (s, 0) = x

(s) ,y(s, 0) = y

(s) ,u(s, 0) = u

(s) .

The solutions of (2.5.65) with the given initial data are

x (s, τ )=

+ τu

(s)+x

(s)

y (s, τ )=τ + y

(s)

u (s, τ )=τ + u

(s)

⎫

⎬

⎭

. (2.5.66)

We choose a particular set of values for the initial data as

x (s, 0) = 2s

,y(s, 0) = 2s, u (s, 0) = 0,s>0.

Therefore, the solutions are given by

x =

+2s

,y= τ +2s, u = τ. (2.5.67)

Eliminating τ and s from (2.5.67) gives the integral surface

(u − y)

+ u

=2x

2u = y ±



4x − y



. (2.5.68)

The solution surface satisfying the data u =0ony

=2x is given by

2u = y −



4x − y



. (2.5.69)

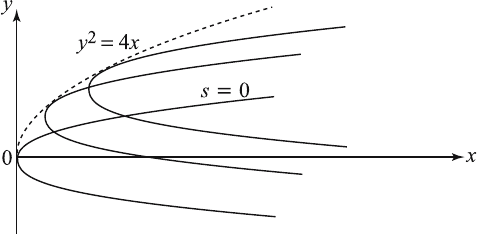
This repr esents the solution surface only when y

< 4x. Thus, the solution

does not exist for y

> 4x and is not diﬀerentiable when y

=4x.Weverify

that y

=4x represents the envelope of the family of characteristics in the

(x, t)-plane given by the τ-eliminant of the ﬁrst two equations in (2.5.67),

that is,

F (x, y, s)=2x − (y − 2s)

− 4s

=0. (2.5.70)

This represents a family of parabolas for diﬀerent values of the parameter

s. Thus, the envelope is obtained by eliminating s from equations

∂F

∂s

and F =0.Thisgivesy

=4x, which is the envelope of the characteristics

for diﬀerent s, as shown in Figure 2.5.2.

2.6 Canonical Forms of First-Order Linear Equations 49

Figure 2.5.2 Dotted curve is the envelope of the characteristics.

2.6 Canonical Forms of First-Order Linear Equations

It is often convenient to transform the more general ﬁrst-order linear partial

diﬀerential equation (2.2.12)

a (x, y) u

+ b (x, y) u

+ c (x, y) u = d (x, y) , (2.6.1)

into a canonical (or standard) form which can be easily integrated to ﬁnd

the general solution of (2.6.1). We use the characteristics of this equation

(2.6.1) to introduce the new transformation by equations

ξ = ξ (x, y) ,η= η (x, y) , (2.6.2)

where ξ and η are once continuously diﬀerentiable and their Jacobian

J (x, y) ≡ ξ

− ξ

is nonzero in a domain of interest so that x and

y can be determined uniq uely from th e system of equations (2.6.2). Thus,

by chain rule,

= u

+ u

= u

+ u

, (2.6.3)

we substitute these partial derivatives (2.6.3) into (2.6.1) to obtain the

equation

+ Bu

+ cu = d, (2.6.4)

where

A = uξ

+ bξ

,B= aη

+ bη

. (2.6.5)

From (2.6.5) we see that B =0ifη is a solution of the ﬁrst-order equation

aη

+ bη

=0. (2.6.6)

This equation has inﬁnitely many solutions. We can obtain one of them

by assigning initial condition on a non-characteristic initial curve and solv-

ing the resulting initial-value problem according to the method described

50 2 First-Order, Quasi-Linear Equations and Method of Characteristics

earlier. Since η (x, y) satisﬁes equation (2.6.6), the level curves η (x, y)=

constant are always characteristic curves of equation (2.6.1). Thus, one set

of the new transformations are the characteristic curves of (2.6.1). The sec-

ond set, ξ (x, y) = constant, can be chosen to be any one parameter family

of smooth curves which are nowhere tangent to the family of the character-

istic curves. We next assert that A = 0 in a neighborhood of some point in

the domain D in which η (x, y) is deﬁned and J =0.For,ifA =0atsome

point of D,thenB = 0 at the same point. Consequently, equations (2.6.5)

would form a system of linear homogeneous equations in a and b, where the

Jacobian J is the determinant of its coeﬃcient matrix . Since J = 0, both a

and b must be zero at that point which contradicts the original assumption

that a and b do not vanish simultaneously. Finally, since B = 0 and A =0

in D, we can divide (2.6.4) by A to obtain the canonical form

+ α (ξ, η) u = β (ξ, η) , (2.6.7)

where α (ξ, η)=

and β (ξ,η)=

Equation (2.6.7) represents an ordinary diﬀerential equation with ξ as

the independent variable and η as a parameter which may be treated as

constant. This equation (2.6.7) is called the canonical for m of equation

(2.6.1) in terms of the coordinates (ξ,η). Generally, the canonical equation

(2.6.7) can easily be integrated and the general solution of (2.6.1) can be

obtained after replacing ξ and η by the original variables x and y.

We close this section by considering some examples that illustrate this

procedure. In practice, it is convenient to choose ξ = ξ (x, y)andη (x, y)=y

or ξ = x and η = η (x, y)sothatJ =0.

Example 2.6.1. Reduce each of the following equations

− u

= u, (2.6.8)

+ u

= x, (2.6.9)

to canonical form, and obtain the general solution.

In (2.6.8), a =1,b = −1, c = −1andd = 0. The characteristic equations

are

−1

Thecharacteristiccurvesareξ = x + y = c

,andwechooseη = y = c

where c

and c

are constants. Consequently, u

= u

and u

= u

+ u

and hence, equation (2.6.8) becomes

= u.

Integrating this equation gives