Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

2.3 Construction of a First-Order Equation 31

solution. Its nature is similar to that of the singular solution of a ﬁrst-order

ordinary diﬀerential equation.

Finally, it is important to note that solutions of a partial diﬀerential

equation are expected to be represented by smooth functions. A function

is called smooth if all of its derivatives exist and are continuous. However,

in general, solutions are not always smooth. A solution which is not ev-

erywhere diﬀerentiable is called a weak solution. The most common weak

solution is t he one that has discontinuities in its ﬁrst partial derivatives

across a curve, so that the solution can be represented by shock waves as

surfaces of discontinuity. In the case of a ﬁrst-order partial diﬀerential equa-

tion, there are discontinuous solutions where z itself and not merely p =

∂z

∂x

and q =

∂z

∂y

are discontinuous. In fact, this kind of discontinuity is usually

known as a shock wave. An important feature of quasi-linear and nonlinear

partial diﬀerential equations is that their solutions may develop disconti-

nuities as they move away from the initial state. We close this section by

considering some examples.

Example 2.3.1. Show that a family of spheres

+ y

+(z − c)

= r

, (2.3.9)

satisﬁes the ﬁrst-order linear partial diﬀerential equation

yp − xq =0. (2.3.10)

Diﬀerentiating the equation (2.3.9) with respect to x and y gives

x + p (z − c)=0 and y + q (z − c)=0.

Eliminating the arbitrary constant c from these equations, we obtain the

ﬁrst-order, partial diﬀerential equation

yp − xq =0.

Example 2.3.2. Show that the family of spheres

(x − a)

+(y − b)

+ z

= r

(2.3.11)

satisﬁes the ﬁrst-order, nonlinear, partial diﬀerential equation



+ q



= r

. (2.3.12)

We diﬀerentiate the equation of the family of spheres with respect to x

and y to obtain

(x − a)+zp=0, (y − b)+zq=0.

Eliminating the two arbitrary constants a and b, we ﬁnd the nonlinear

partial diﬀerential equation

32 2 First-Order, Quasi-Linear Equations and Method of Characteristics



+ q



= r

All surfaces of revolution with the z-axis as the axis of symmetry satisfy

the equation

z = f



+ y



, (2.3.13)

where f is an arbitrary function. Writing u = x

+ y

and diﬀerentiating

(2.3.13) with respect to x and y, respectively, we obtain

p =2xf

′

(u) ,q=2yf

′

(u) .

Eliminating the arbitrary function f (u) from these results, we ﬁnd the

equation

yp − xq =0.

Theorem 2.3.1. If φ = φ (x, y, z)andψ = ψ (x, y, z) are two given func-

tions of x, y,andz and if f (φ, ψ) = 0, where f is an arbitrar y function of φ

and ψ,thenz = z (x, y) satisﬁes a ﬁrst-order, partial diﬀerential equation

∂ (φ, ψ)

∂ (y, z)

+ q

∂ (φ, ψ)

∂ (z, x)

∂ (φ, ψ)

∂ (x, y)

, (2.3.14)

where

∂ (φ, ψ)

∂ (x, y)



. (2.3.15)

Proof. We diﬀerentiate f (φ, ψ) = 0 with respect to x and y respectively

to obtain the following equations:

∂f

∂φ



∂φ

∂x

+ p

∂φ

∂z



∂f

∂ψ



∂ψ

∂x

+ p

∂ψ

∂z



=0, (2.3.16)

∂f

∂φ



∂φ

∂y

+ q

∂φ

∂z



∂f

∂ψ



∂ψ

∂y

+ q

∂ψ

∂z



=0. (2.3.17)

Nontrivial solutions for

∂f

∂φ

and

∂f

∂ψ

can be found if the determinant of

the coeﬃcients of these equations vanishes, that is,



+ pφ

+ pψ

+ qφ

+ qψ



=0. (2.3.18)

Expanding this determinant gives the ﬁrst-order, quasi-linear equation

(2.3.14).

2.4 Geometrical Interpretation of a First-Order Equation 33

2.4 Geometrical Interpretation of a First-Order

Equation

To investigate the geometrical content of a ﬁrst-order, partial diﬀerential

equation, we begin with a general, quasi-lin ear equation

a (x, y, u) u

+ b (x, y, u) u

− c (x, y, u)=0. (2.4.1)

We assume that the possible solution of (2.4.1) in the form u = u (x, y)

or in an implicit form

f (x, y, u) ≡ u (x, y) − u = 0 (2.4.2)

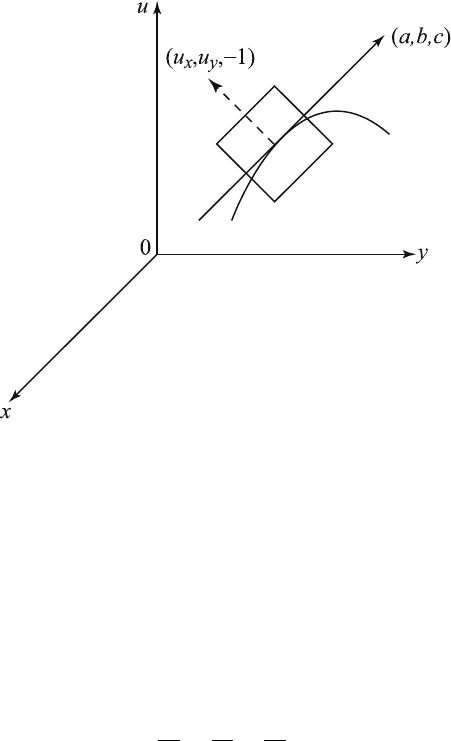
represents a possible solution surface in (x, y, u) space. This is often called

an integral surface of the equation (2.4.1). At any point (x, y, u)onthe

solution surface, the gradient vector ∇f =(f

)=(u

, −1) is

normal to th e solution surface. Clearly, equation (2.4.1) can be written as

the dot product of two vectors

+ bu

− c =(a, b, c) · (u

− 1) = 0. (2.4.3)

This clearly shows that the vector (a, b, c) must be a tangent vector of

the integral surface (2.4.2) at the point (x, y, u), and hence, it determines

a direction ﬁeld called the the characteristic direction or Monge axis.This

direction is of fundamental importance in determining a solution of equation

(2.4.1). To summarize, we have shown that f (x, y, u)=u (x, y) − u =0,

as a surface in the (x, y, u)-space, is a solution of (2.4.1) if and only if the

direction vector ﬁeld (a, b, c) lies in the tangent plane of the integral surface

f (x, y, u) = 0 at each point (x, y, u), where ∇f = 0, as shown in Figure

2.4.1.

Acurvein(x, y, u)-space, whose tangent at every point coincides with

the characteristic direction ﬁeld (a, b, c), is called a characteri stic curve.If

the parametric equations of this characteristic curve are

x = x (t) ,y= y (t) ,u= u (t) , (2.4.4)

then the tangent vector to th is curve is





which must be equal

to (a, b, c). Therefore, the system of ordinary diﬀerential equations of the

characteristic curve is given by

= a (x, y, u) ,

= b (x, y, u) ,

= c (x, y, u) . (2.4.5)

These are called the characteristic equations of the quasi-linear equation

(2.4.1).

34 2 First-Order, Quasi-Linear Equations and Method of Characteristics

Figure 2.4.1 Tangent and normal vector ﬁelds of solution surface a t a point

(x, y, u).

In fact, there are only two independent ordinary diﬀerential equations

in the system (2.4.5); therefore, its solutions consist of a two-parameter

family of curves in (x, y, u)-space.

The projection on u = 0 of a characteristic curve on the (x, t)-plane is

called a characteristic base curve or simply characteristic.

Equivalently, the characteristic equations (2.4.5) in the nonparametric

form are

. (2.4.6)

The typical problem of solving equation (2.4.1) with a prescribed u on

a given plane curve C is equivalent to ﬁnding an integral surface in (x, y, u)

space, satisfying the equation (2.4.1) and containing the three-dimensional

space curve Γ deﬁned by the values of u on C, which is the projection on

u =0ofΓ .

Remark 1. The above geometrical interpretation can be generalized for

higher-order partial diﬀerential equations. However, it is not easy to visu-

alize geometrical arguments that have been described for the case of three

space dimensions.

Remark 2. The geometrical interpretation is more complicated for the case

of nonlinear partial d iﬀerential equations, because the normals to possible

2.5 Method of Characteristics and General Solutions 35

solution surfaces through a point do not lie in a plane. The tangent planes

no longer intersect along one straight line, but instead, they envelope along

a curved surface known as the Monge cone. Any further discussion is beyond

the scope of this book.

We conclude this section by adding an important observation regarding

the nature of the characteristics in the (x, t)-plane. For a quasi-linear equa-

tion, characteristics are determined by the ﬁrst two equations in (2.4.5)

with their slopes

b (x, y, u)

a (x, y, u)

. (2.4.7)

If (2.4.1) is a li near equation, th en a and b are independent of u, and the

characteristics of (2.4.1) ar e plane curves with slopes

b (x, y)

a (x, y)

. (2.4.8)

By integrating this equation, we can determine the characteristics which

represent a one-parameter family of curves in the (x, t)-plane. However, if

a and b are constant, the characteristics of equation (2.4.1) are straight

lines.

2.5 Method of Characteristics and General Solutions

We can use the geometrical interpretation of ﬁrst-order, partial diﬀerential

equations an d the properties of characteristic curves to develop a method

for ﬁnding the general solution of quasi-linear equations. This is usually

referred to as the method of characteristics due to Lagrange. This method

of solution of quasi-linear equations can be described by the following result.

Theorem 2.5.1. The general solution of a ﬁrst-order, quasi-linear partial

diﬀerential equation

a (x, y, u) u

+ b (x, y, u) u

= c (x, y, u) (2.5.1)

f (φ, ψ)=0, (2.5.2)

where f is an arbitrary function of φ (x, y, u)andψ (x, y, u), and φ =

constant = c

and ψ = constant = c

are solution curves of the charac-

teristic equations

. (2.5.3)

The solution curves deﬁned by φ (x, y, u)=c

and ψ (x, y, u)=c

are

called the families of characteri stic curves of equation (2.5.1).

36 2 First-Order, Quasi-Linear Equations and Method of Characteristics

Proof. Since φ (x, y, u)=c

and ψ (x, y, u)=c

satisfy equations (2.5.3),

these equations must be compatible with the equation

dφ = φ

dx + φ

dy + φ

du =0. (2.5.4)

This is equivalent to the equation

aφ

+ bφ

+ cφ

=0. (2.5.5)

Similarly, equation (2.5.3) is also compatible with

aψ

+ bψ

+ cψ

=0. (2.5.6)

We now solve (2.5.5), (2.5.6) for a, b,andc to obtain

∂(φ,ψ)

∂(y,u)

∂(φ,ψ)

∂(u,x)

∂(φ,ψ)

∂(x,y)

. (2.5.7)

It has been shown earlier that f (φ, ψ) = 0 satisﬁes an equation similar to

(2.3.14), that is,

∂ (φ, ψ)

∂ (y, u)

+ q

∂ (φ, ψ)

∂ (u, x)

∂ (φ, ψ)

∂ (x, y)

. (2.5.8)

Substituting, (2.5.7) in (2.5.8), we ﬁnd that f (φ, ψ) = 0 is a solution of

(2.5.1). This completes the proof.

Note that an analytical method has been used to prove Theorem 2.5.1.

Alternatively, a geometrical argument can be used to prove this theorem.

The geometrical method of proof is left to the reader as an exercise.

Many problems in applied mathematics, science, an d engineering involve

partial diﬀerential equations. We seldom try to ﬁnd or discuss the properties

of a solution to these equations in its most general form. In most cases of

interest, we deal with those solutions of partial diﬀerential equations which

satisfy certain supplementary conditions. In the case of a ﬁrst-order partial

diﬀerential equation, we determine the speciﬁc solution by formulating an

initial-value problem or a Cauchy problem.

Theorem 2.5.2. (The Cauchy Problem for a First-Order Partial Diﬀeren-

tial Equation). Supp ose that C is a given curve in the (x, y)-plane with its

parametric equations

x = x

(t) ,y= y

(t) , (2.5.9)

where t belongs to an interval I ⊂ R, and the derivatives x

′

(t)andy

′

(t)are

piecewise continuous functions, such that (x

′

)

+(y

′

)

= 0. Also, suppose

that u = u

(t) is a given function on the curve C. Then, there exists a

solution u = u (x, y) of the equation

2.5 Method of Characteristics and General Solutions 37

F (x, y, u, u

) = 0 (2.5.10)

in a domain D of R

containing the curve C for all t ∈ I, and the solution

u (x , y) satisﬁes the given initial data, that is,

u (x

(t) ,y

(t)) = u

(t) (2.5.11)

for all values of t ∈ I.

In short, the Cauchy problem is to determine a solution of equation

(2.5.10) in a neighborhood of C, such that the solution u = u (x, y) takes a

prescribed value u

(t)onC.ThecurveC is called the initial curve of the

problem, and u

(t) is called the initial data. Equation (2.5.11) is called the

initial condition of the problem.

The solution of the Cauchy problem also deals with such questions as

the conditions on the fun ctions F , x

(t), y

(t), and u

(t) under which a

solution exists and is unique.

We next discuss a method for solving a Cauchy problem for the ﬁrst-

order, quasi-linear equation (2.5.1). We ﬁrst observe that geometrically

x = x

(t), y = y

(t), and u = u

(t) represent an initial curve Γ in

(x, y, u)-space. The curve C, on which the Cauchy data is prescribed, is

the projection of Γ on the (x, y)-plane. We now present a p recise formula-

tion of the Cauchy problem for the ﬁrst-order, quasi-linear equation (2.5.1).

Theorem 2.5.3. (The Cauchy Problem for a Quasi-linear Equation). Sup-

pose that x

(t), y

(t), and u

(t) are continuously diﬀerentiable functions

of t in a closed interval, 0 ≤ t ≤ 1, and that a, b,andc are functions of

x, y,andu with continuous ﬁrst-order partial derivatives with respect to

their arguments in some domain D of (x, y, u)-space containing the initial

curve

Γ : x = x

(t) ,y= y

(t) ,u= u

(t) , (2.5.12)

where 0 ≤ t ≤ 1, and satisfying the condition

′

(t) a (x

(t) ,y

(t) ,u

(t)) − x

′

(t) b (x

(t) ,y

(t) ,u

(t)) =0. (2.5.13)

Then there exists a uni que solution u = u (x, y) of the quasi-linear equation

(2.5.1) in the neighborhood of C : x = x

(t), y = y

(t), and the solution

satisﬁes the initial condition

(t)=u (x

(t) ,y

(t)) , for 0 ≤ t ≤ 1. (2.5.14)

Note: The cond ition (2.5.13) excludes the possibility that C could be a

characteristic.

Example 2.5.1. Find the general solution of the ﬁrst-order linear partial

diﬀerential equation.

38 2 First-Order, Quasi-Linear Equations and Method of Characteristics

+ yu

= u. (2.5.15)

The characteristic curves of this equation are the solutions of the char-

acteristic equations

. (2.5.16)

This system of equations gives the integral surfaces

φ =

= C

and ψ =

= C

where C

and C

are arbitrary constants. Thus, the general solution of

(2.5.15) is





=0, (2.5.17)

where f is an arbitrary function. This general solution can also be written

u (x , y)=xg





, (2.5.18)

where g is an arbitrary function.

Example 2.5.2. Obtain the general solution of the linear Euler equation

+ yu

= nu. (2.5.19)

The integral surfaces are the solutions of the characteristic equations

. (2.5.20)

From these equations, we get

= C

where C

and C

are arbitrary constants. Hence, the general solution of

(2.5.19) is





=0. (2.5.21)

This can also be written as

= g





u (x , y)=x





. (2.5.22)

This shows that the solution u (x, y) is a homogeneous function of x and y

of degree n.

2.5 Method of Characteristics and General Solutions 39

Example 2.5.3. Find the general solution of the linear equation

+ y

=(x + y) u. (2.5.23)

The characteristic equations associated with (2.5.23) are

(x + y) u

. (2.5.24)

From the ﬁrst two of these equations, we ﬁnd

−1

− y

−1

= C

, (2.5.25)

where C

is an arbitrary constant.

It follows from (2.5.24) that

dx − dy

− y

(x + y) u

d (x − y)

x − y

This gives

x − y

= C

, (2.5.26)

where C

is a constant. Furthermore, (2.5.25) and (2.5.26) also give

= C

, (2.5.27)

where C

is a constant.

Thus, the general solution (2.5.23) is given by



x − y



=0, (2.5.28)

where f is an arbitrar y function. This general solution representing the

integral surface can also be written as

u (x , y)=xy g



x − y



, (2.5.29)

where g is an arbitrary function, or, equivalently,

u (x , y)=xy h



x − y



, (2.5.30)

where h is an arbitrary function.

40 2 First-Order, Quasi-Linear Equations and Method of Characteristics

Example 2.5.4. Show that the general solution of the linear equation

(y − z) u

+(z − x) u

+(x − y) u

= 0 (2.5.31)

u (x , y, z)=f



x + y + z, x

+ y

+ z



, (2.5.32)

where f is an arbitrary function.

The characteristic curves satisfy the characteristic equations

y − z

z − x

x − y

(2.5.33)

du =0,dx+ dy + dz =0,xdx+ ydy + zdz =0.

Integration of these equations gives

u = C

,x+ y + z = C

, and x

+ y

+ z

= C

where C

, C

and C

are arbitrary constants.

Thus, the general solution can be written in terms of an arbitrary func-

tion f in the form

u (x , y, z)=f



x + y + z, x

+ y

+ z



We next verify that this is a general solution by introducing three inde-

pendent variables ξ,η,ζ deﬁned in terms of x, y,andz as

ξ = x + y + z, η = x

+ y

+ z

, and ζ = y + z, (2.5.34)

where ζ is an arbitrary combination of y and z. Clearly the general solution

becomes

u = f (ξ, η) ,

and hence,

= u

∂x

∂ζ

+ u

∂y

∂ζ

+ u

∂z

∂ζ

. (2.5.35)

It follows from (2.5.34) that

∂x

∂ζ

∂y

∂ζ

∂z

∂ζ

, 0=2



∂x

∂ζ

+ y

∂y

∂ζ

+ z

∂z

∂ζ



∂y

∂ζ

∂z

∂ζ

=1.

It follows from the ﬁrst and the third results that

∂x

∂ζ

= −1 and, therefore,

x = y

∂y

∂ζ

+ z

∂z

∂ζ

,y= y

∂y

∂ζ

+ y

∂z

∂ζ

,z= z

∂y

∂ζ

+ z

∂z

∂ζ