Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

4.3 Equations with Constant Coeﬃcients 101

ξ = x, η = x − (B/C) y. (4.3.8)

Under this transformation, equation (4.3.5) reduces to the canonical form

ξη

= D

∗

+ E

∗

+ F

∗

u + G

∗

(ξ,η) , (4.3.9)

where D

∗

, E

∗

,andF

∗

are constants.

The canonical form of the Euler equation (4.3.6) is

ξη

=0. (4.3.10)

Integrating this equation gives the general solution

u = φ (ξ)+ψ (η)=φ (y − λ

,x)+ψ (y − λ

,x) , (4.3.11)

where φ and ψ are arbitrary functions, and λ

and λ

are given by (4.3.3).

(B) Parabolic Type

When B

− 4AC = 0, the equation is of parabolic type, in which case

only one real family of characteristics exists. From equation (4.3.4), we ﬁnd

that

= λ

=(B/2A) ,

so that the single family of characteristics is given by

y =(B/2A) x + c

where c

is an integrati on constant. Thus, we have

ξ = y − (B/2A) x, η = hy + kx, (4.3.12)

where η is chosen arbitrarily such that the Jacobian of the transformation

is not zero, and h and k are constants.

With the proper choice of the constants h and k in the transformation

(4.3.12), equation (4.3.5) reduces to

ηη

= D

+ E

+ F

u + G

(ξ,η) , (4.3.13)

where D

, E

,andF

are constants.

If B = 0, we can see at once from the relation

− 4AC =0,

that C or A vanishes. The given equation is then already in the canonical

form. Similarly, in the other cases when A or C vanishes, B vanishes. The

given equation is is then also in canonical form.

The canonical form of the Euler equation (4.3.6) is

ηη

=0. (4.3.14)

102 4 Classiﬁcation of Second-Order Linear Equations

Integrating twice gives the general solution

u = φ (ξ)+ηψ(ξ) , (4.3.15)

where ξ and η are given by (4.3.12). Choosing h =1,k = 0 and λ =





for simplicity, the general solution of the Euler equation in the parabolic

case is

u = φ (y − λx)+yψ(y − λx) . (4.3.16)

When B

− 4AC < 0, the equation is of elliptic type. In this case, the

characteristics are complex conjugates.

The characteristic equations yield

y = λ

x + c

,y= λ

x + c

, (4.3.17)

where λ

and λ

are complex numbers. Accordingly, c

and c

are allowed

to take on complex values. Thus,

ξ = y − (a + ib) x, η = y − (a − ib) x, (4.3.18)

where λ

1,2

= a +

ib in which a and b are real constants, and

a =

, and b =



4AC − B

Introduce the new variables

α =

(ξ + η)=y − ax, β =

(ξ − η)=−bx. (4.3.19)

Application of this transformation readily reduces equation (4.3.5) to the

canonical form

αα

+ u

ββ

= D

+ E

+ F

u + G

(α, β) , (4.3.20)

where D

, E

, F

are constants.

We note that B

− AC < 0, so neither A nor C is zero.

In this elliptic case, the Euler equation (4.3.6) gives the complex char-

acteristics (4.3.18) which are

ξ =(y − ax) − ibx, η =(y − ax)+ibx =

ξ. (4.3.21)

Consequently, the E ul er equation becomes

ξξ

=0, (4.3.22)

with the general solution

u = φ (ξ)+ψ





. (4.3.23)

The appearance of complex arguments in the general solution (4.3.23) is a

general feature of elliptic equations.

4.3 Equations with Constant Coeﬃcients 103

Example 4.3.1. Consider the equation

4 u

+5u

+ u

=2.

Since A =4,B =5,C =1,andB

− 4AC =9> 0, the equation is

hyperb oli c. Thus, the characteristic equations take the form

=1,

and hence, the characteristics are

y = x + c

,y=(x/4) + c

The linear transformation

ξ = y − x, η = y − (x/4) ,

therefore reduces the given equ ation to the canonical form

ξη

−

This is the ﬁrst canonical form.

The second canonical form may be obtained by the transformation

α = ξ + η, β = ξ − η,

in the form

αα

− u

ββ

−

Example 4.3.2. The equation

− 4 u

+4u

= e

is parabolic since A =1,B = −4, C =4,andB

− 4AC =0.Thus,we

have from equation (4.3.12)

ξ = y +2x, η = y,

in which η is chosen arbitrarily. By means of this mapping, the equation

transforms into

ηη

Example 4.3.3. Consider the equation

+ u

=0.

104 4 Classiﬁcation of Second-Order Linear Equations

Since A =1,B =1,C =1,andB

− 4AC = −3 < 0, the equation is

elliptic.

We have

1,2

B +

√

− 4AC

√

and hence,

ξ = y −



+ i

√



x, η = y −



− i

√



Introducing the new variables

α =

(ξ + η)=y −

x, β =

(ξ − η)=−

√

the given equation is then transformed into canonical form

αα

+ u

ββ

√

Example 4.3.4. Consider the wave equation

− c

=0,cis constant.

Since A = −c

, B =0,C =1,andB

− 4AC =4c

> 0, the wave

equation is hyperbolic everywhere. According to (4.2.4), the equation of

characteristics is

−c





+1=0,

− c

=0.

Therefore,

x + ct = ξ = constant,x− ct = η = constant.

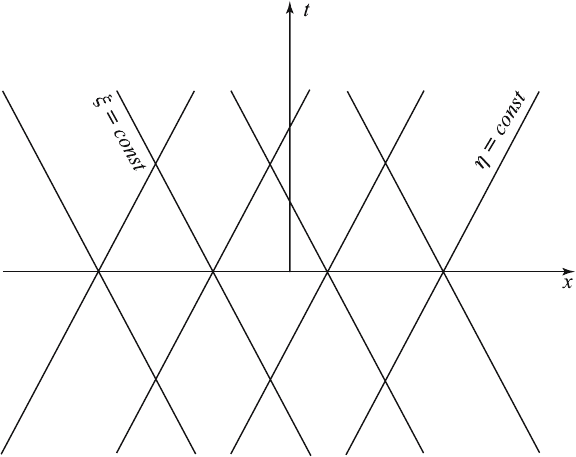
Thus, the characteristics are straight lines, which are shown in Figure 4.3.1.

The characteristics form a natural set of coordinates for the hyperbolic

equation.

In terms of new coordinates ξ and η deﬁned above, we obtain

= u

ξξ

+2u

ξη

+ u

ηη

= c

ξξ

− 2u

ξη

+ u

ηη

) ,

so that the wave equation becomes

4.3 Equations with Constant Coeﬃcients 105

Figure 4.3.1 Characteristics for the wave equation.

−4c

ξη

=0.

Since c =0,wehave

ξη

=0.

Integrating with respect to ξ, we obtain

= ψ

(η) .

where ψ

is the arbitrar y function of η. Integrating with respect to η,we

obtain

u (ξ ,η)=



(η) dη + φ (ξ) .

If we set ψ (η)=

(η) dη, the general solution becomes

u (ξ ,η)=φ (ξ)+ψ (η) ,

which is, in terms of the original variables x and t,

u (x , t)=φ (x + ct)+ψ (x − ct) ,

provided φ and ψ are arbitrary but twice diﬀerentiable functions.

106 4 Classiﬁcation of Second-Order Linear Equations

Note that φ is constant on “wavefronts” x = −ct + ξ that travel toward

decreasing x as t increases, whereas ψ isconstantonwavefrontsx = ct + η

that travel toward increasing x as t increases. Thus, any general solution

can be expressed as the sum of two waves, one traveling to the right with

constant velocity c and the other traveling to the left with the same velocity

Example 4.3.5. Find the characteristic equat ions and characteristics, and

then reduce the equations



sech



=0, (4.3.24ab)

to the canonical forms.

In equation (4.3.24a), A =1,B = 0 and C = −sech

x. Hence,

− 4AC = 4 sech

x>0.

Hence, the equation is hyperbolic. The characteristic equations are

B +

√

− 4AC

sech

Integration gives

+ tanh x = constant.

Hence,

ξ = y + tanh x, η = y − tanh x.

Using these characteristic coordinates, the given equation can be trans-

formed into the canonical form

ξη

(η − ξ)

4 − (ξ − η)

− u

) . (4.3.25)

In equation (4.3.24b), A =1,B = 0 and C = sech

x. Hence,

− 4AC =+

i sech

Integrating gives

+ i tanh x = constant.

Thus,

ξ = y + i tanh x, η = y − i tanh x.

The new real variables α and β are

4.4 General Solutions 107

α =

(ξ + η)=y, β =

(ξ − η) = tanh x.

In terms of these new variables, equation (4.3.24b) can be transformed into

the canonical form

αα

+ u

ββ

2β

1 − β

, |β| < 1. (4.3.26)

Example 4.3.6. Consider the equation

+ (2 cosecy) u



cosec



=0. (4.3.27)

In this case, A =1,B = 2 cosecy and C = cosec

y. Hence, B

− 4AC =0,

and

= cosec y.

The characteristic curves are therefore given by

ξ = x +cosy and η = y.

Using these variables, the canonical form of (4.3.27) is

ηη



sin

η cos η



. (4.3.28)

4.4 General Solutions

In general, it is not so simple to determine the general solution of a given

equation. Sometimes further simpliﬁcation of the canonical form of an equa-

tion may yield the general solution. If the canonical form of the equation

is simple, then the general solution can be immediately ascertained.

Example 4.4.1. Find the general solution of

+2xy u

+ y

=0.

In Example 4.2.2, using the transformation ξ = y/x, η = y, this equation

was reduced to the canonical form

ηη

=0, for y =0.

Integrating twice with respect to η, we obtain

u (ξ ,η)=ηf (ξ)+g (ξ) ,

where f (ξ)andg (ξ) are arbitrary functions. In terms of the independent

variables x and y,wehave

u (x , y)=yf





+ g





108 4 Classiﬁcation of Second-Order Linear Equations

Example 4.4.2. Determine the general solution of

4 u

+5u

+ u

=2.

Using the transformation ξ = y − x, η = y − (x/4), the canonical form of

this equation is (see Example 4.3.1)

ξη

−

By means of the substitution v = u

, the preceding equation reduces to

v −

This can be easily integrated by separating the variables. Integrating with

respect to ξ,wehave

v =

(ξ/3)

F (η) .

Integrating with respect to η, we obtain

u (ξ ,η)=

η +

g (η) e

ξ/3

+ f (ξ) ,

where f (ξ)andg (η) are arbitrary functions. The general solution of the

given equation becomes

u (x , y)=



y −





y −



(y −x)

+ f (y − x) .

Example 4.4.3. Obtain the general solution of

3 u

+10u

+3u

=0.

Since B

−4AC =64> 0, the equation is hyperbolic. Thus, from equation

(4.3.2), the characteristics are

y =3x + c

,y=

x + c

Using the transformations

ξ = y − 3x, η = y −

the given equation can be reduced to the form





ξη

=0.

4.4 General Solutions 109

Hence, we obtain

ξη

=0.

Integration yields

u (ξ ,η)=f (ξ)+g (η) .

In terms of the original variables, the general solution is

u (x , y)=f (y − 3x)+g



y −



Example 4.4.4. Find the general solution of the following equations

+3yu

+3u

=0,y=0, (4.4.1)

+2u

+ u

=0, (4.4.2)

+2u

+5u

+ u

=0. (4.4.3)

In equation (4.4.1), A = y, B =3y, C =0,D =3,E = F = G =0.

Hence B

− 4AC =9y

> 0 and the equation is hyperbolic for all points

(x, y)withy = 0. Consequently, the characteristic equations are

B +

√

− 4AC

3y +

=3, 0.

Integrating gives

y = c

and y =3x + c

Thecharacteristiccurvesare

ξ = y and η = y − 3x.

In terms of these variables, the canonical form of (4.4.1) is

ξu

ξη

+ u

=0.

Writing v = u

and using the integrating factor gives

v = u

C (η) ,

where C (η) is an arbitrary function.

Integrating again with respect to η gives

u (ξ ,η)=



C (η) dη + g (ξ)=

f (η)+g (ξ) ,

where f and g are arbitrary functions. Finally, in terms of the original

variables, the general solution i s

110 4 Classiﬁcation of Second-Order Linear Equations

u (x , y)=

f (y − 3x)+g (y) . (4.4.4)

Equation (4.4.2) has coeﬃcients A =1,B =2,C =1,D = E = F =

G = 0. Hence, B

−4AC = 0, the equation is parabolic. The characteristic

equation is

=1,

and the characteristics are

ξ = y − x = c

and η = y.

Using these variables, equation (4.4.2) takes the canonical form

ηη

=0.

Integrating twice gives the general solution

u (ξ ,η)=ηf(ξ)+g (ξ) ,

where f and g are arbitrary functions.

In terms of x and y, this solution becomes

u (x , y)=yf(y − x)+g (y − x) . (4.4.5)

The coeﬃcients of equation (4.4.3) ar e A =1,B =2,C =5,E =1,

F = G = 0 and hence B

− 4AC = −16 < 0, equation (4.4.3) is elliptic.

The characteristic equations are

=(1+

2i) .

The characteristics are

y =(1−2i) x + c

,y=(1+2i) x + c

and hence,

ξ = y − (1 − 2i) x, η = y − (1 + 2i) x,

and new real variables α and β are

α =

(ξ + η)=y − x, η =

(ξ − η)=2x.

The canonical form is given by

αα

+ u

ββ

− 2 u

) . (4.4.6)

It is not easy to ﬁnd a general solution of (4.4.6).