Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


8.6 Bessel’s Equation and Bessel’s Function 291
J
−n
(x)=
∞
k=n
(−1)
k
x
2k−n
2
2k−n
k! Γ (−n + k +1)
.
=(−1)
n
∞
k=0
(−1)
k
x
2k+n
2
2k+n
k! Γ (n + k +1)
.
=(−1)
n
J
n
(x) . (8.6.15)
This shows that J
−n
is not independent of J
n
, and therefore, a second
linearly independent solution is required.
A number of distinct irregular solutions are discussed in the literature,
but the one most commonly used, as defined by Watson (1966), is
Y
ν
(x)=
(cos νπ) J
ν
(x) − J
−ν
(x)
sin νπ
. (8.6.16)
For nonintegral ν, it is obvious that Y
ν
(x), being a linear combination of
J
ν
(x)andJ
−ν
(x), is linearly independent of J
ν
(x). When ν is a nonneg-
ative integer n, Y
ν
(x) is indeterminate. But
Y
n
(x) = lim
ν→n
Y
ν
(x)
exists and is a solution of the Bessel equation. Moreover, it is linearly in-
dependent of J
n
(x). (For an extended treatment, see Watson (1966)). The
function Y
ν
(x) is called the Bessel function of the second kind of order ν.
Thus, the general solution of the Bessel equation is
y (x)=c
1
J
ν
(x)+c
2
Y
ν
(x) , for ν ≥ 0. (8.6.17)
Like elementary functions, the Bessel functions are tabu lated (see Jah nke
et al. (1960)). For illustration, the functions J
0
, J
1
, Y
0
and Y
1
are plotted
for small values of x in Figure 8.6.1.
It should be noted that J
ν
(x)forν ≥ 0andJ
−ν
(x) for a positive
integer ν are finite at the origin, but J
−ν
(x) for nonintegral ν and Y
ν
(x)
for ν ≥ 0 approach infinity as x tends to zero.
Some of the useful recurrence relations are
J
ν−1
(x)+J
ν+1
(x)=
2ν
x
J
ν
(x) , (8.6.18)
νJ
ν
(x)+xJ
′
ν
(x)=xJ
ν−1
(x) , (8.6.19)
J
ν−1
(x) − J
ν+1
(x)=2J
′
ν
(x) , (8.6.20)
νJ
ν
(x) − xJ
′
ν
(x)=xJ
ν+1
(x) , (8.6.21)
d
dx
[x
ν
J
ν
(x)] = x
ν
J
ν−1
(x) , (8.6.22)
d
dx
x
−ν
J
ν
(x)
!
= −x
−ν
J
ν+1
(x) . (8.6.23)
All of these relations also hold true for Y
ν
(x).
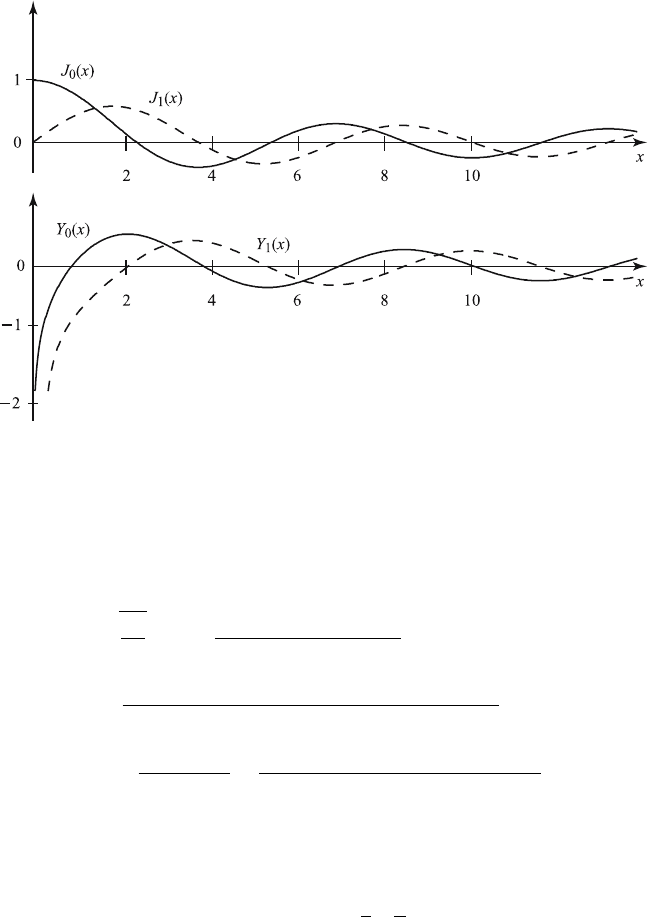
292 8 Eigenvalue Problems and Special Functions
Figure 8.6.1 Graphs of J
ν
(x) and Y
ν
(x).
For |x|≫1and|x|≫ν, the asymptotic expansion of J
ν
(x)is
J
ν−1
(x) ∼
2
πx
/
1 −
4ν
2
− 1
2
4ν
2
− 3
2
2! (8x)
2
+
4ν
2
− 1
2
4ν
2
− 3
2
4ν
2
− 5
2
4ν
2
− 7
2
4! (8x)
4
− ...
0
cos φ
−
/
4ν
2
− 1
2
8x
−
4ν
2
− 1
2
4ν
2
− 3
2
4ν
2
− 5
2
3! (8x)
3
+ ...
0
sin φ
(8.6.24)
where
φ = x −
ν +
1
2
π
2
.
For |x|≫1and|x|≫ν, the asymptotic expansion of Y
ν
(x)is
8.6 Bessel’s Equation and Bessel’s Function 293
Y
ν
(x) ∼
2
πx
/
1 −
4ν
2
− 1
2
4ν
2
− 3
2
2! (8x)
2
+
4ν
2
− 1
2
4ν
2
− 3
2
4ν
2
− 5
2
4ν
2
− 7
2
4! (8x)
4
− ...
0
sin φ
+
/
4ν
2
− 1
2
8x
−
4ν
2
− 1
2
4ν
2
− 3
2
4ν
2
− 5
2
3! (8x)
3
+ ...
0
cos φ
.
(8.6.25)
When ν =+
(1/2), Bessel’s f unction may be expressed in the form
J
1
2
(x)=
2
πx
sin x, (8.6.26)
J
−
1
2
(x)=
2
πx
cos x. (8.6.27)
The Bessel fun ctions which satisfy the condition
J
ν
(ak
m
)+hJ
′
ν
(ak
m
)=0,h,a= constant, (8.6.28)
are orthogonal to each other with respect to the weight function x,thatis,
for the nonnegative integer ν, the orthogonal relation is
a
0
xJ
ν
(xk
n
) J
ν
(xk
m
) dx =0,n= m. (8.6.29)
When n = m,wehavethenorm
J
ν
(xk
m
)
2
=
a
0
x [J
ν
(xk
m
)]
2
dx
=
1
2k
2
m
(
a
2
k
2
m
[J
′
ν
(ak
m
)]
2
+
a
2
k
2
m
− ν
2
[J
ν
(ak
m
)]
2
)
,
(8.6.30)
where k
m
are the roots of (8.6.28).
We now give a particular example of the eigenfunction expansion the-
orem discussed in Sections 8.4 and 8.5. Assume a formal expansion of the
function f (x)definedin0≤ x ≤ a in the form
f (x)=
∞
m=1
a
m
J
ν
(xk
m
) , (8.6.31)
where the summation is taken over all the positive roots k
1
, k
2
, k
3
, ...,
of equation (8.6.28). Multiplying (8.6.31) by xJ
ν
(xk
n
), integrating, and
utilizing (8.6.30), we obtain
294 8 Eigenvalue Problems and Special Functions
a
0
xf (x) J
ν
(xk
m
) dx = a
m
a
0
x [J
ν
(xk
m
)]
2
dx
=
a
m
2k
2
m
(
a
2
k
2
m
[J
′
ν
(ak
m
)]
2
+
a
2
k
2
m
− ν
2
[J
ν
(ak
m
)]
2
)
. (8.6.32)
Thus, we have the following theorem:
Theorem 8.6.1. If
b
m
=
a
0
xf (x) J
ν
(xk
m
) dx (8.6.33)
then the expansion (8.6.31) of f (x) takes the form
f (x)=
∞
m=1
2k
2
m
b
m
J
ν
(xk
m
)
k
2
m
[J
′
ν
(ak
m
)]
2
+(a
2
k
2
m
− ν
2
)[J
ν
(ak
m
)]
2
. (8.6.34)
In particular, when h =0in (8.6.28), that is, when k
m
are the positive
roots of J
ν
(ak
m
)=0, then (8.6.34) becomes
f (x)=
2
a
2
∞
m=1
b
m
J
ν
(xk
m
)
k
2
m
[J
′
ν
(ak
m
)]
2
=
2
a
2
∞
m=1
b
m
J
ν
(xk
m
)
[J
ν+1
(ak
m
)]
2
. (8.6.35)
These expansions are known as the Bessel–Fourier series for f (x). They
are generated by Sturm–Liouville problems involving the Bessel equation,
and arise from problems associated with partial differential equations.
Closely related to Bessel’s functions are Hankel’s functions of the first
and second kind, defined by
H
(1)
ν
(x)=J
ν
(x)+iY
ν
(x) ,H
(2)
ν
(x)=J
ν
(x) − iY
ν
(x) , (8.6.36)
respectively, where i =
√
−1.
Other closely related functions are the modified Bessel functions. Con-
sider Bessel’s equation containing a parameter λ,namely,
x
2
y
′′
+ xy
′
+
λ
2
x
2
− ν
2
y =0. (8.6.37)
The general solution of this equation is
y (x)=c
1
J
ν
(λx)+c
2
Y
ν
(λx) .
If λ = i,then
y (x)=c
1
J
ν
(ix)+c
2
Y
ν
(ix) .
We write

8.7 Adjoint Forms and Lagrange Identity 295
J
ν
(ix)=
∞
k=0
(−1)
k
(ix)
2k+ν
2
2k+ν
k! Γ (ν + k +1)
= i
ν
I
ν
(x) ,
where
I
ν
(x)=
∞
k=0
x
2k+ν
2
2k+ν
k! Γ (ν + k +1)
, (8.6.38)
I
ν
(x) is called the modified Bessel function of the first kind of order ν.
As in the case of J
ν
and J
−ν
, I
ν
and I
−ν
(which is defined in a similar
manner) are linearly independent solutions except when ν is an integer.
Consequently, we define the modified Bessel function of the second kind of
order ν by
K
ν
(x)=
π
2
I
−ν
(x) − I
ν
(x)
sin νπ
. (8.6.39)
Thus, we obtain the general solution of the modified Bessel equation
x
2
y
′′
+ xy
′
−
x
2
+ ν
2
y = 0 (8.6.40)
in the form
y (x)=c
1
I
ν
(x)+c
2
K
ν
(x) . (8.6.41)
We should note that
I
ν
(0) =
⎧
⎨
⎩
1,ν=0
0,ν>0
(8.6.42)
and that K
ν
approaches infinity as x → 0.
For a detailed treatment of Bessel and related functions, refer to Wat-
son’s (1966) Theory of Bessel Functions.
The eigenvalue problems which involve Bessel’s functions will be de-
scribed in Section 8.8 on singular Sturm–Liouville systems.
8.7 Adjoint Forms and Lagrange Identity
Self-adjoint equations play a very important role in many areas of applied
mathematics and mathematical physics. Here we will give a brief account
of self-adjoint operators and the Lagrange identity.
We consider the equation
L [y]=a
0
(x) y
′′
+ a
1
(x) y
′
+ a
2
(x) y =0

296 8 Eigenvalue Problems and Special Functions
definedonanintervalI. Integrating z (x) L [y] by parts from a to x,we
have
x
a
zL[y] dx =
(za
0
) y
′
− (za
0
)
′
y +(za
1
) y
!
x
a
+
x
a
(za
0
)
′′
− (za
1
)
′
+(za
2
)
!
ydx. (8.7.1)
Now, if we define the second-order operator L
∗
by
L
∗
[z]=(za
0
)
′′
− (za
1
)
′
+(za
2
)=a
0
z
′′
(2a
′
0
− a
1
) z
′
+(a
′′
0
− a
′
1
+ a
2
) z
the relation (8.7.1) takes the form
x
a
(zL[y] − yL
∗
[z]) dx =[a
0
(y
′
z − yz
′
)+(a
1
− a
′
0
) yz ]
x
a
. (8.7.2)
The operator L
∗
is called the adjoint operator correspondin g to the operator
L. It can be readily verified that the adjoint of L
∗
is L itself. If L and L
∗
are
the same, L is said to be self-adjoint. The necessary and sufficient condition
for this is that
a
1
=2a
′
0
− a
1
,a
2
= a
′′
0
− a
′
1
+ a
2
,
which is satisfied if
a
1
= a
′
0
.
Thus, if L i s self-adjoint, we have
L (y)=a
0
y
′′
+ a
′
0
y
′
+ a
2
y
=(a
0
y
′
)
′
+ a
2
(x) y. (8.7.3)
In general, L [y] is not self-adjoint. But if we let
h (x)=
1
a
0
exp
x
a
1
(t)
a
0
(t)
dt
(8.7.4)
then h (x) L [y] is self-adjoint. Thus, any second-order linear differential
equation
a
0
(x) y
′′
+ a
1
(x) y
′
+ a
2
(x) y = 0 (8.7.5)
can be made self-adjoint. Multiplying by h (x) given by equation (8.7.4),
equation (8.7.5) is transformed into the self-adjoint form
d
dx
p (x)
dy
dx
+ q (x) y =0, (8.7.6)
8.8 Singular Sturm–Liouville Systems 297
where
p (x)=exp
x
a
1
(t)
a
0
(t)
dt
,q(x)=
a
2
a
0
exp
x
a
1
(t)
a
0
(t)
dt
. (8.7.7)
For example, the self-adjoint form of the Legendre equation
1 − x
2
y
′′
− 2xy
′
+ n (n +1)y =0
is
d
dx
1 − x
2
dy
dx
+ n (n +1)y =0, (8.7.8)
and the self-adjoint form of the Bessel equation
x
2
y
′′
+ xy
′
+
x
2
− ν
2
y =0
is
d
dx
x
dy
dx
+
x −
ν
2
x
y =0. (8.7.9)
Now, if we differentiate both sides of equation (8.7.2), we obtain
zL[y] − yL
∗
[z]=
d
dx
[a
0
(y
′
z − yz
′
)+(a
1
− a
′
0
) yz ] (8.7.10)
which is known as the Lagrange identity for the operator L.
If we consider the integral from a to b of equation (8.7.2), we obtain
Green’s identity
b
a
(zL[y] − yL
∗
[z]) dx =[a
0
(y
′
z − yz
′
)+(a
1
− a
′
0
) yz ]
b
a
. (8.7.11)
When L is self-adjoint, this relation becomes
b
a
(zL[y] − yL [z]) dx =[a
0
(y
′
z − yz
′
)]
b
a
. (8.7.12)
8.8 Singular Sturm–Liouville Systems
A Sturm–Liouville equation is called singular when it is given on a semi-
infinite or infinite interval, or when the coefficient p (x)ors (x) vanishes, or
when one of the coefficients becomes infinite at one end or both ends of a
finite interval. A singular Sturm–Liouville equation together with appropri-
ate linear homogeneous end conditions is called a singular Sturm–Liouville
(SSL) system. The condition s i mposed in this case are not like the sepa-
rated boundary end conditions in the regular Sturm–Liouville system. The
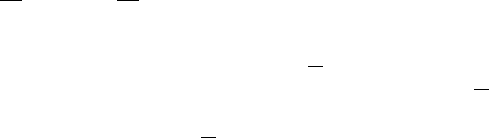
298 8 Eigenvalue Problems and Special Functions
condition that is often necessary to pr escribe is the boundedness of the
function y (x) at the singular end point. To exhibit this, let us consider a
problem with a singularity at the end point x = a. By the relation (8.7.12),
for any twice continuously differentiable functions y (x)andz (x), we have
on (a, b)
b
a+ε
{zL[y] − yL [z]}dx = p (b)[y
′
(b) z (b) − y (b) z
′
(b)]
−p (a + ε)[y
′
(a + ε) z (a + ε) − y (a + ε) z
′
(a + ε)] ,
where ε is a small positive number. If the conditions
lim
x→a+
p (x)[y
′
(x) z (x) − y (x) z
′
(x)]=0, (8.8.1)
p (b)[y
′
(b) z (b) − y (b) z
′
(b)]=0, (8.8.2)
are imposed on y and z, it follows that
b
a
{zL[y] − yL [z]}dx =0. (8.8.3)
For example, when p (a) = 0, the relations (8.8.1) and (8.8.2) are replaced
by the conditions
1. y (x)andy
′
(x) are finite as x → a
2. b
1
y (b)+b
2
y
′
(b)=0.
Thus, we say that the singular Sturm–Liouville system is self-adjoint,if
any functions y (x)andz (x) that satisfy the end conditions satisfy
b
a
{zL[y] − yL [z]}dx =0.
Example 8.8.1. Consider the singular Sturm–Liouville system involving Leg-
endre’s equation
d
dx
1 − x
2
dy
dx
+ λy =0, −1 <x<1,
with the conditions that y and y
′
are finite as x → +
1.
In this case, p (x)=1−x
2
and s (x) = 1, and p (x) vanishes at x =+
1.
The Legendre functions of the first kind, P
n
(x), n =0, 1, 2,..., are the
eigenfunctions which are finite as x → +
1. The corresponding eigenvalues
are λ
n
= n (n +1) for n =0, 1, 2,.... We observe here that the singu-
lar Sturm–Liouville system has infinitely many real eigenvalues, and the
eigenfunctions P
n
(x) are orthogonal to each other.
Example 8.8.2. Another example of a singular Sturm–Liouville system is
the Bessel equat ion for fixed ν

8.8 Singular Sturm–Liouville Systems 299
d
dx
x
dy
dx
+
λx−
ν
2
x
y =0, 0 <x<a,
with the end conditions that y (a)=0andy and y
′
are finite as x → 0+.
Here p (x)=x, q (x)=−
ν
2
x
,ands (x)=x.Nowp (0) = 0, q (x) becomes
infinite as x → 0+, and s (0) = 0; therefore, the system is singular. If λ = k
2
,
the eigenfunction s of the system are the Bessel functions of the first kind of
order ν, namely J
ν
(k
n
x), n =1, 2, 3,...,wherek
n
a is the nth zero of J
ν
.
The Bessel function J
ν
and its derivative are both finite as x → 0+. The
eigenvalu es are λ
n
= k
2
n
. Thus, the system has infinitely many eigenvalues,
and the eigenfunctions are orthogonal to each other with respect to the
weight function s (x)=x.
In the preceding examples, we have seen that the eigenfunctions are
orthogonal with respect to the weight function s (x). In general, the eigen-
functions of a singular Sturm–Liouville system are orthogonal if they are
square-integrable with respect to the weight function s (x)=x.
Theorem 8.8.1. The square-integrable eigenfunctions corresponding to dis-
tinct eigenvalues of a singular Sturm–Liouville system are orthogonal with
respect to the weight function s (x).
Proof. Proceeding as in Theorem 8.2.1, we arrive at
(λ
j
− λ
k
)
b
a
sφ
j
φ
k
dx = p (b)
φ
j
(b) φ
′
k
(b) − φ
′
j
(b) φ
k
(b)
!
−p (a)
φ
j
(a) φ
′
k
(a) − φ
′
j
(a) φ
k
(a)
!
.
Suppose the boundary term vanishes, as in the case mentioned earlier, where
p (a)=0,y and y
′
are finite as x → a, and at the other end b
1
y (b)+
b
2
y
′
(b) = 0. Then, we have
(λ
j
− λ
k
)
b
a
sφ
j
φ
k
dx =0.
This integral exists by virtue of (8.3.2). Thus, for distinct eigenvalues λ
j
=
λ
k
, the square-integrable functions φ
j
and φ
k
are orthogonal with respect
to the weight function s (x).
Example 8.8.3. Consider the singular Sturm–Liou ville system involving the
Hermite equation
u
′′
− 2xu
′
+ λu =0, −∞ <x<∞, (8.8.4)
which is not self-adj oint.
If we l et y (x)=e
−x
2
/2
u (x), the Hermite equation takes the self-adjoint
form
y
′′
+
1 − x
2
+ λ
!
y =0, −∞ <x<∞.
300 8 Eigenvalue Problems and Special Functions
Here p =1,q (x)=1− x
2
, s = 1. The eigenvalues are λ
n
=2n for
nonnegative integers n, and the corresponding eigenfunctions are φ
n
(x)=
e
−x
2
/2
H
n
(x), where H
n
(x) are the Hermite polynomials which are so-
lutions of the Hermite equation (8.8.4) (See Magnus and Oberhettinger
(1949)).
Now, we impose the end conditions that y tends to zero as x → +
∞.
This is satisfied because H
n
(x) are polynomials in x and in fact x
n
e
−x
2
/2
→
0asx → +
∞.Sinceφ
n
(x) are square-integrable, we have
∞
−∞
H
m
(x) H
n
(x) e
−x
2
dx =0,m= n.
Example 8.8.4. Consider the problem of the transverse vibration of a thin
elastic circular membrane
u
tt
= c
2
u
rr
+
1
r
u
r
,r<1,t>0,
u (r, 0) = f (r) ,u
t
(r, 0) = 0, 0 ≤ r ≤ 1, (8.8.5)
u (1,t)=0, lim
r→0
u (r, t) < ∞,t≥ 0.
We seek a nontrivial separable solution in the f orm
u (r, t)=R (r) T (t) .
Substituting this in the wave equation yields
R
′′
+(1/r) R
′
R
=
1
c
2
T
′′
T
= −α
2
,
where α is a positive constant. The negative sign in front of α
2
is chosen to
obtain the solution periodic in time. Thus, we have
rR
′′
+ R
′
+ α
2
rR =0,T
′′
+ α
2
c
2
T =0.
The solution T (t) is therefore given by
T (t)=A cos (αct)+B sin (αct) .
Next, it is required to determine the solution R (r) of the following
singular Sturm–Liouville system
d
dr
r
dR
dr
+ α
2
rR =0, (8.8.6)
R (1) = 0, lim
r→0
R (r) < ∞. (8.8.7)
We note that in this case, p = r which vanishes at r = 0. The condition on
the boundedness of the function R (r) is obtained from the fact that
lim
r→0
u (r, t) = lim
r→0
R (r) T (t) < ∞
