Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

8.2 Eigenvalues and Eigenfunctions 281

Theorem 8.2.7. An eigenfunction of a regular Sturm–Liouville system is

unique except for a constant factor.

Proof.Letφ

(x)andφ

(x) be eigenfunctions corresponding to an eigen-

value λ. Then, according to Abel’s formula (8.2.16), we have

p (x) W (x; φ

,φ

) = constant,p(x) > 0,

where W is the Wronskian. Thus, if W vanishes at a point in [a, b], it must

vanish for all x ∈ [a, b].

Since φ

and φ

satisfy the end condition at x = a,wehave

(a)+a

′

(a)=0,

(a)+a

′

(a)=0.

Since a

and a

are not both zero, we have



(a) φ

′

(a)

(a) φ

′

(a)



= W (a; φ

,φ

)=0.

Therefore, W (x; φ

) = 0 for all x ∈ [a, b], which is a suﬃcient condition

for the linear dependence of two functions φ

and φ

. Hence, φ

(x)diﬀers

from φ

(x) only by a constant factor.

Theorem 8.2.5 states that all eigenvalues of a regular Sturm–Liouville

system are real, but it does not guarantee that any eigenvalue exists. How-

ever, it can be proved that a self-adjoint regular Sturm–Liou ville system

has a denumerably inﬁnite number of eigenvalues. To illustrate this, we

consider the followin g example.

Example 8.2.1. Consider the Sturm–Liouville system

′′

+ λy =0, 0 ≤ x ≤ 1,

y (0) = 0,y(1) + hy

′

(1) = 0,h>0 a constant.

Here p =1,q =0,s = 1. The solution of the Sturm–Liouville equation

y (x)=A cos

√

λx+ B sin

√

λx.

Since y (0) = 0, gives A =0,wehave

y (x)=B sin

√

λx.

Applying the second end condition, we have

sin

√

λ + h

√

λ cos

√

λ =0,B=0

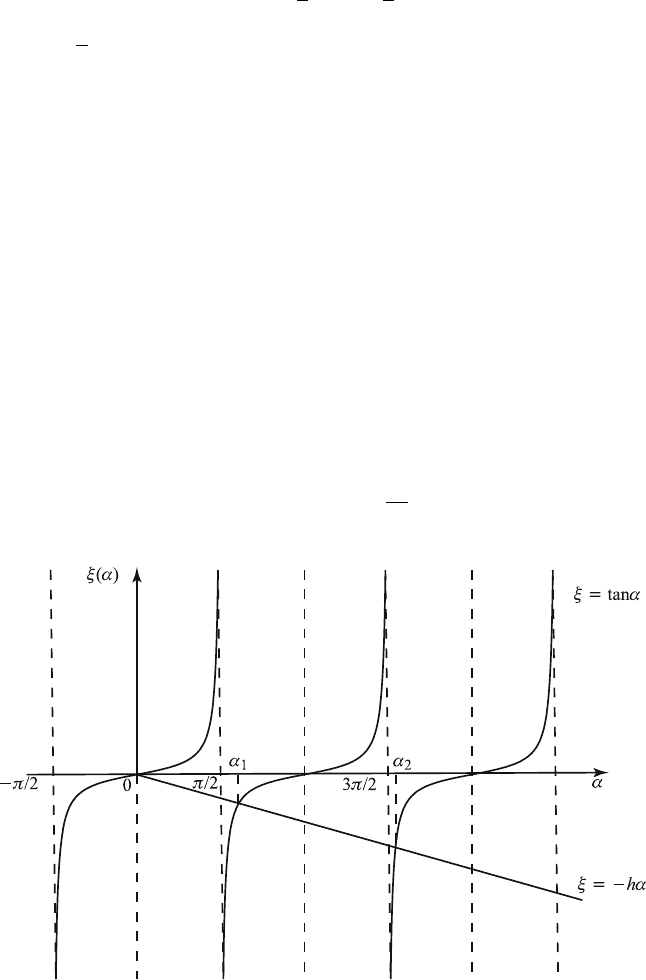
282 8 Eigenvalue Problems and Special Functions

which can be rewritten as

tan

√

λ = −h

√

λ.

If α =

√

λ is introduced in this equation, we have

tan α = −hα.

This equation does not possess an explicit solution. Thus, we determine

the solution graphically by plotting the functions ξ = tan α and ξ = −hα

against α, as shown in Figure 8.2.1. The roots are given by the intersection

of two curves, and as is evident from the graph, there are inﬁnitely many

roots α

for n =1, 2, 3,.... To each root α

, th ere corresponds an eigenvalue

= α

,n=1, 2, 3,....

Thus, there exists an ordered sequence of eigenvalues

<λ

<...

with

lim

n→∞

= ∞.

The corresponding eigenfunctions are sin



√



Figure 8.2.1 Intersection of ξ =tanα and ξ = −hα.

8.3 Eigenfunction Expansions 283

Theorem 8.2.8. A self-adjoint regular Sturm –Liouville system has an in-

ﬁnite sequence of real eigenvalues

<λ

<...

with

lim

n→∞

= ∞.

For each n the corresponding eigenfunction φ

(x), uniquely determined up

to a constant factor, has exactly n zeros in the interval (a, b).

Proof of this theorem can be found in the book by Myint-U (1978).

8.3 Eigenfunction Expansions

A real-valued function φ (x) is said to be square-integrable with respect to

a weight function ρ (x) > 0,if,onanintervalI,



(x) ρ (x) dx < +∞. (8.3.1)

An immediate consequence of this deﬁnition is the Schwarz inequality





φ (x) ψ (x) ρ (x) dx



≤



(x) ρ (x) dx



(x) ρ (x) dx (8.3.2)

for square-integrable functions φ (x)andψ (x).

Let {φ

(x)}, for positive integers n, be an orthogonal set of square-

integrable functions with a positive weight function ρ (x)onaninterval

I.Letf (x) be a given function that can be represented by a uniformly

convergent series of the form

f (x)=

∞



n=1

(x) , (8.3.3)

where the coeﬃcients c

are constants. Now multiplying both sides of (8.3.3)

by φ

(x) ρ (x) and integrating term by term over the interval I (uniform

convergence of the series is a suﬃcient condition for this), we obtain



f (x) φ

(x) ρ (x) dx =

∞



n=1



(x) φ

(x) ρ (x) dx,

and hence, for n = m,



f (x) φ

(x) ρ (x) dx = c



(x) ρ (x) dx.

284 8 Eigenvalue Problems and Special Functions

Thus,

fφ

ρdx

. (8.3.4)

Hence, we have the following theorem:

Theorem 8.3.1. If f is represented by a uniformly convergent series

f (x)=

∞



n=1

(x)

on an interval I, where φ

are square-integrable functions orthogonal with

respect to a positive weight function ρ (x), then c

are determined by

fφ

ρdx

Example 8.3.1. The Legendre polynomials P

(x) are orthogonal with re-

spect to the weight function ρ (x)=1on(−1, 1). If we assume that f (x)

can be represented by the Fourier–Legendre series

f (x)=

∞



n=1

(x)

then, c

are given by

−1

f (x) P

(x) dx

−1

(x) dx



2n +1





−1

f (x) P

(x) dx.

In the above discussion, we assumed that the given function f (x)is

represented by a uniformly convergent series. This is rather restrictive, and

we will show in the following section that f (x) can be represented by a

mean-square convergent series.

8.4 Convergence in the Mean

Let {φ

} be the set of square-integrable functions or thogon al with respect

to a weight function ρ (x)on[a, b]. Let

(x)=



k=1

(x)

8.4 Convergence in the Mean 285

be the nth partial sum of the series

∞



k=1

(x).

Let f be a square-integrable function. The sequence {s

} is said to

converge in the mean to f (x) on the interval I with respect to the weight

function ρ (x)if

lim

n→+∞



[f (x) − s

(x)]

ρ (x) dx =0. (8.4.1)

We shall now seek the coeﬃcients c

such that s

(x) represents the

best approximation to f (x) in the sense of least squares, that is, we seek

to minimize the integral

E (c



[f (x) − s

(x)]

ρ (x) dx



ρdx− 2



k=1



fφ

ρdx+



k=1



ρdx. (8.4.2)

This is an extremal prob lem. A necessary condition on the c

for E to

be minimum is that the ﬁrst partial derivatives of E wi th respect to these

coeﬃcients vanish. Thus, diﬀerentiating (8.4.2) with respect to c

, we obtain

∂E

∂c

= −2



fφ

ρdx+2c



ρdx = 0 (8.4.3)

and hence,

fφ

ρdx

. (8.4.4)

Now if we complete the square, the right side of (8.4.2) becomes

E =



ρdx+



k=1



ρdx



−

fφ

ρdx



−



k=1



fφ

ρdx



ρdx

The right side shows that E is a minimum if and only if c

is given by

(8.4.4). Therefore, this choice of c

yields the best approximation to f (x)

in the sense of least squares.

For series convergent in the mean to f (x), we conventionally write

f (x) ∼

∞



k=1

(x) ,

where the coeﬃcients c

are the generalized Fourier coeﬃcients and the

seriesisthegeneralized Fourier series. This series may or may not be point-

wise or uniformly convergent.

286 8 Eigenvalue Problems and Special Functions

8.5 Completeness and Parseval’s Equality

Substituting the Fourier coeﬃcients (8.4.4) into (8.4.2), we obtain





f (x) −



k=1

(x)



ρ (x) dx =



ρdx−



k=1



ρdx.

Since the left side is nonnegative, we have



k=1



ρdx ≤



ρdx. (8.5.1)

The integral on the right side is ﬁnite, and hence, th e series on the left side

is bounded above for any n.Thus,asn →∞, the inequality (8.5.1) may

be wri tten as

∞



k=1



ρdx ≤



ρdx. (8.5.2)

This is called Bessel’s inequality.

If the series converges in the mean to f (x), that is,

lim

n→∞





f (x) −



k=1

(x)



ρ (x) dx =0,

then, it follows from the above derivation that

∞



k=1



ρdx =



ρdx

which is called Parseval’s equality. Sometimes it is known as the complete-

ness relation. Thus, when every continuous square-integrable function f (x)

can be expanded into an inﬁnite series

f (x)=

∞



k=1

(x) ,

the sequence of continuous square-integrable functions {φ

} orthogonal

with respect to the weight function ρ is said to be complete.

Next we state the following theorem:

Theorem 8.5.1. The eigenfunctions of any regular Sturm–Li ouville sys-

tem are complete in the space of functions that are piecewise continuous

on the interval [a, b] with respect to the weight function s (x). Moreover ,

any piecewise smooth function on [a, b] that satisﬁes the end conditions of

8.5 Completeness and Parseval’s Equality 287

the regular Sturm–Liouville system can be expanded in an absolutely and

uniformly convergent series

f (x)=

∞



k=1

(x) ,

where c

are given by



fφ

s (x) dx



s (x) dx.

Proof of a more general theorem can be found in Coddington and Levinson

(1955).

Example 8.5.1. Consider a cylindrical wire of length l whose surface is per-

fectly insulated against the ﬂow of heat. The end l = 0 is maintained at the

zero degree temperature, while the other end rad iates freely into the sur-

rounding medium of zero degree temperature. Let the initial temperature

distribution in the wire be f (x). Find the temperature distribution u (x, t).

The initial boundary-value problem is

= ku

, 0 <x<l, t>0, (8.5.3)

u (x , 0) = f (x) , 0 <x≤ l, (8.5.4)

u (0,t)=0,t>0, (8.5.5)

hu(l, t)+u

′

(l, t)=0,t>0,h>0. (8.5.6)

By the method of separation of variables, we assume a nontrivial solu-

tion in the form

u (x , t)=X (x) T (t)

and substituting it in the heat equation, we obtain

′′

+ λX =0,T

′

+ kλT =0,

where λ>0 is a separation constant. The solution of the latter equation is

T (t)=Ce

−kλt

(8.5.7)

where C is an arbitrary constant. The former equation has to be solved

subject to the boundary conditions

X (0) = 0,hX(l)+X

′

(l)=0.

This is a Sturm–Liouville system which gives the solution with X (0) = 0

X (x)=B sin

√

λx, (8.5.8)

288 8 Eigenvalue Problems and Special Functions

where B is a constant to be determined.

Application of the second end condition (8.5.6) yields

h sin

√

λl+

√

λ cos

√

λl =0 for B =0

which can be rewritten as

tan

√

λl = −

√

λ/h.

If α =

√

λl is introduced in the preceding equation, we have

tan α = −aα,

where a =(1/hl). As in Example 8.2.1, there exists a sequence of eigenval-

ues

<λ

<...

with lim

n→∞

= ∞. The corresponding eigenfunctions are sin

√

x,and

hence,

(x)=B

sin



x. (8.5.9)

Therefore, combining (8.5.7) with C = C

and (8.5.9), the solution takes

the form

(x, t)=a

−kλ

sin



x, a

= B

which satisﬁes the heat equation and the boundary conditions. Since the

heat equation is linear and homogeneous, we form the series solution

u (x , t)=

∞



n=1

−kλ

sin



x, (8.5.10)

which is also a solution, provided it converges and is twice diﬀerentiable

with respect to x and once d iﬀerentiable with respect to t. According to

Theorem 8.2.1, the eigenfunctions sin

√

x form an orthogonal system

over the interval (0,l). Application of the initial condition yields

u (x , 0) = f (x) ∼

∞



n=1

sin



If we assume that f is a piecewise smooth function on [a, b],then,byTheo-

rem 8.5.1, we can expand f (x) in terms of the eigenfunctions, and formally

write

f (x)=

∞



n=1

sin



where the coeﬃcient a

is given by



f (x)sin



xdx



sin



xdx.

With this value of a

, the temperature distribution is given by (8.5.10).

8.6 Bessel’s Equation and Bessel’s Function 289

8.6 Bessel’s Equation and Bessel’s Function

Bessel’s equation frequently occurs in problems of applied mathematics and

mathematical physics involving cylindrical symmetry.

The standard form of Bessel’s equation is given by

′′

+ xy

′



− ν



y =0, (8.6.1)

where ν is a nonnegative real number. We shall ﬁrst restrict our attention

to x>0. Since x = 0 is the regular singu lar point, a solution is taken in

accordance with the Frobenius method to be

y (x)=

∞



n=0

s+n

, (8.6.2)

where the index s is to be determined. Substitution of th is series into equa-

tion (8.6.1) then yields



− ν



(s +1)

− ν

s+1

∞



n=2

(s + n)

− ν

+ a

n−2

)

s+n

=0. (8.6.3)

The requirement that the coeﬃcient of x

vanish leads to the initial equation



− ν



=0, (8.6.4)

from which it follows that s =+

ν for arbitrary a

= 0. Since the leading

term in the series (8.6.2) is a

, it is clear that for ν>0 the solution of

Bessel’s equation corresponding to the choice s = ν vanishes at the origin,

whereas the solu tion corresponding to s = −ν is inﬁnite at that point.

We consider ﬁrst the regular solution of Bessel’s equation, that is, the

solution corresponding to the choice s = ν. The vanishing of the coeﬃcient

of x

s+1

in equation (8.6.3) requires that

(2ν +1)a

=0, (8.6.5)

whichinturnimpliesthata

=0(sinceν ≥ 0). From th e requirement that

the coeﬃcient of x

s+n

in equation (8.6.3) be zero, we obtain the two-term

recurrence relation

= −

n−2

n (2ν + n)

. (8.6.6)

Since a

= 0, it is obvious that a

=0forn =3, 5, 7,.... The remaining

coeﬃcients are given by

(−1)

k!(ν + k)(ν + k − 1) ...(ν +1)

(8.6.7)

290 8 Eigenvalue Problems and Special Functions

for k =1, 2, 3,.... This relation may also be written as

(−1)

Γ (ν +1)a

2k+ν

k!Γ (ν + k +1)

,k=1, 2,..., (8.6.8)

where Γ (α) is the gamma function, whose properties are described in the

Appendix.

Hence, the regular solution of Bessel’s equation takes the form

y (x)=a

∞



k=0

(−1)

Γ (ν +1)

2k+ν

k!Γ (ν + k +1)

2k+ν

. (8.6.9)

It is customary to choose

Γ (ν +1)

(8.6.10)

and to denote the corresponding solution by J

(x). This solution, called

the Bessel function of the ﬁrst kind of order ν, is therefore given by

(x)=

∞



k=0

(−1)

2k+ν

k! Γ (ν + k +1)

. (8.6.11)

To determine the irregular solution of the Bessel equation for s = −ν,

we proceed as above. In this way, we obtain as the analogue of equation

(8.6.5) the relation

(−2ν +1)a

from which it follows, without loss of generality, that a

= 0. Using the

recurrence relation

= −

n−2

n (n − 2ν)

,n≥ 2 (8.6.12)

we obtain the irregular solution of the Bessel function of the ﬁrst kind of

order −ν as

−ν

(x)=

∞



k=0

(−1)

2k−ν

k! Γ (−ν + k +1)

. (8.6.13)

It can be easily proved that, if ν is not an integer, J

and J

−ν

converge

for all values of x, and are linearly independent. Thus, the general solution

of the Bessel equation for nonintegral ν is

y (x)=c

(x)+c

−ν

(x) . (8.6.14)

If ν is an integer, say ν = n, then from equation (8.6.13), noting that,

when gamma functions in the coeﬃcients of the ﬁ rst n terms become inﬁ-

nite, the coeﬃcients become zero, hence we have