Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

26 1. Continuous Population Models for Single Species

that the period of the growing unstable solution is approximately 4T .Thisisleftasan

exercise (Exercise 6).

In fact, the experimentally observed period is of the order of two to three times the

estimated delay time. The model here for carbon dioxide in the blood is a simple one

and to make detailed quantitative comparison with the actual process that takes place

is not really justiﬁed. It does, however, clearly show how a delay model can arise in a

genuine physiological context and produce oscillatory behaviour such as is observed in

Cheyne–Stokes respiration.

The problem of periodic breathing that we have just discussed has also been studied

in some detail by Fowler and Kalamangalam (2000; see other references there). They

put forward a very different explanation for the disease. They suggest that the dynamics

of the system are determined by the interaction between the carbon dioxide in the differ-

ent compartments of the body and that, in fact, the production is more or less irrelevant.

They show that the respiratory system is subject to an oscillatory instability when, as

with patients with heart failure, the cardiac output is severely reduced. They further

show that the cycle time is approximately twice the brain arterial delay and show that

this is consistent with recent observational studies on patients with cardiac problems.

They go further and include variable cardiac response to blood gas levels, which in turn

introduces variable delays, and show that this has a stabilising effect. An important as-

pect of their work is the extensive discussion they give of the physiological implications

of parameter variation in their model.

There are many fascinating and challenging modelling problems associated with

breathing; see, for example, the book of articles edited by Benchetrit et al. (1987). Also,

periodic breathing is not restricted to pathologies of the heart and brain. See also the

book by Hoppensteadt and Peskin (1992) for other physiological examples.

Regulation of Haematopoiesis

The second example we consider brieﬂy has certain similarities to the last and so we

do not go through the analysis in as much detail. It is concerned with the regulation of

haematopoiesis, the formation of blood cell elements in the body. For example, white

and red blood cells, platelets and so on are produced in the bone marrow from where

they enter the blood stream. When the level of oxygen in the blood decreases this leads

to a release of a substance which in turn causes an increase in the release of the blood

elements from the marrow. There is thus a feedback from the blood to the bone marrow.

Abnormalities in the feedback system are considered major suspects in causing periodic

haematological diseases in general and this one is no exception. Further details of the

process and the model we discuss are given in Mackey and Glass (1977) and Glass and

Mackey (1979).

Let c(t) be the concentration of cells (the population species) in the circulating

blood; the units of c are, say, cells/mm

. We assume that the cells are lost at a rate pro-

portional to their concentration, that is, like gc, where the parameter g has dimensions

(day)

−1

. After the reduction in cells in the blood stream there is about a 6-day delay

before the marrow releases further cells to replenish the deﬁciency. We thus assume

that the ﬂux λ of cells into the blood stream depends on the cell concentration at an

earlier time, namely, c(t −T ),whereT is the delay. Such assumptions suggest a model

1.5 Delay Models in Physiology: Periodic Dynamic Diseases 27

equation of the form

dc(t)

= λ(c(t − T )) − gc(t). (1.42)

Mackey and Glass (1977) proposed two possible forms for the function λ(c(t − T)).

The one we consider gives

λa

c(t − T )

(t − T )

− gc, (1.43)

where λ, a, m, g and T are positive constants. This equation can be analysed in the same

way as (1.28) above (Exercise 5). The procedure is to nondimensionalise it, look for the

steady state, investigate the linear stability and determine the conditions for instability.

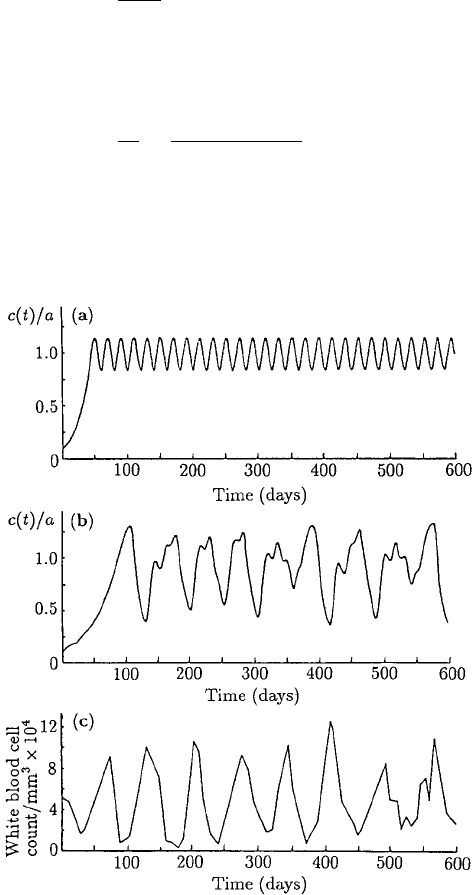
Figure 1.15. (a) Numerical solution of (1.43), the model for haematopoiesis (regulation of blood cells) with

parameter values g = 0.1day

−1

, λ = 0.2day

−1

, m = 10, and delay T = 6 days. The low amplitude

oscillation has a period of about 20 days. (b) The numerical simulation with parameter values as in (a) except

for an increase in the delay to T = 20 days. Note the aperiodic behaviour of the solution. (c) Circulating

blood count of a 12-year-old girl suffering from chronic leukaemia. The rough period of the oscillation is

about 72 days. (Redrawn from Mackey and Glass 1977).

28 1. Continuous Population Models for Single Species

Near the bifurcation values of the parameters which initiate an oscillatory growing so-

lution a perturbation analysis provides an estimate for the period of the ensuing limit

cycle behaviour. Figures 1.15(a) and (b) show the numerical simulation of (1.43) for

two values of the delay time T and parameters in the range for which the steady state is

unstable.

One manifestation of leukaemia is the periodic oscillations observed in, for exam-

ple, the white cell count. Figure 1.15(c) is an example from a 12-year-old patient with

chronic myelogenous leukaemia. Although the overall character is quasi-periodic, it is

in fact aperiodic. Note the comparison between Figures 1.15(b) and (c).

The qualitative change in the solution behaviour as the delay is increased is indica-

tive of what is now referred to as chaos. We discuss this concept in more detail in the

following chapter. Basically chaos is when the solution pattern is not repetitive in any

regular way. A working deﬁnition of chaos is aperiodic behaviour in a deterministic

system which depends intimately on the initial conditions: very small changes in the

initial conditions can give rise to major differences in the solution at later times. An

indication of periodic behaviour and of the onset of chaos can be obtained from the plot

of c(t −T ) against c(t) for various values of the parameters. Figure 1.16 shows a series

of bifurcating periodic solutions of (1.43) as the parameter m increases.

The behaviour in Figure 1.16(a), where the phase plane trajectory is a simple closed

curve, implies the solution is a simple periodic solution. For example, if we start at P

say, the solution trajectory moves round the curve and eventually returns to P after a

ﬁnite time. In other words if c(t) = c

at time t

, c(t) is again equal to c

when time t

increases by the period: Figure 1.15(a) is a typical solution c(t) as a function of time in

this situation. If we now look at Figure 1.16(b) it looks a bit like a double loop trajectory

of the kind in (a); you have to go round twice to return to where you started. A typical

solution here is like that shown in Figure 1.17(a).

The solutions c(t) implied by Figure 1.16 illustrate a common and important feature

of many model systems, namely, different periodic solution behaviour as a parameter

passes through speciﬁc bifurcation values; here it is the Hill coefﬁcient m in (1.43).

Referring now to Figure 1.17(b), if you start at P the solution ﬁrst decreases with

time and then increases as you move along the trajectory of the ﬁrst, inner, loop. Now

when c(t) reaches Q, instead of going round the same loop past P again it moves onto

the outer loop through R. It eventually goes through P again after the second circuit. As

before the solution is still periodic of course, but its appearance is like a mixture of two

solutions of the type in Figure 1.15(a) but with different periods and amplitudes. As m

increases, the phase plane trajectories become progressively more complex suggesting

quite complex solution behaviour for c(t). For the case in Figure 1.16(e) the solution

undergoes very many loops before it possibly returns to its starting point. In fact it never

does! The solutions in such cases are not periodic although they have a quasi-periodic

appearance. This is an example of chaotic behaviour.

Figure 1.15(b) is a solution of (1.43) which exhibits this chaotic behaviour while

Figure 1.15(c) shows the dynamic behaviour of the white cell count in the circulating

blood of a leukaemia patient. Although Figures 1.15(b) and (c) exhibit similar aperiodic

behaviour, it is dangerous to presume that this model is therefore the one governing

white cell behaviour in leukaemia patients. However, what this modelling exercise has

demonstrated, among other things, is that delay can play a signiﬁcant role in physiologi-

1.5 Delay Models in Physiology: Periodic Dynamic Diseases 29

Figure 1.16. Numerical solutions of bifurcating periodic solutions of the model for haematopoiesis given by

(1.43) with γ = a = 1, λ = 2, T = 2, and a range of m from m = 7tom = 20. Note the progression from

a simple periodic solution, as indicated by (a), to the complex chaotic behaviour indicated by (e). For larger

m, regular periodic solutions again emerge prior to another chaotic range as in (i).Seetextforadetailed

explanation. (Reproduced with permission from Mackey and Milton 1988)

cal pattern disruption. In turn this suggests that a deﬁciency in bone marrow cell produc-

tion could account for the erratic behaviour in the white cell count. So although such a

model can highlight important questions for a medical physiologist to ask, for it to be of

practical use it is essential that close interdisciplinary collaboration is maintained so that

realism is retained in making suggestions and drawing conclusions, however plausible

they may be.

30 1. Continuous Population Models for Single Species

(b)(a)

c(t)

c(t − T )

Figure 1.17. (a) Qualitative solution for c(t) when the parameters in the differential delay equation (1.28)

have a phase plane trajectory as in (b), namely, the case in Figure 1.13(b).

The numerical simulations of this differential delay model (1.43), which is clearly

illustrative of a whole class, indicates a cascading sequence of bifurcating periodic solu-

tions which become chaotic. The sequence then passes through a coherent periodic stage

and again becomes chaotic and so on as a parameter in the model itself passes through

successive bifurcating values. As we said, this behaviour arises in a different context in

the following chapter on discrete models where it is discussed in some detail: periodic

doubling can be shown analytically. This phenomenon of cascading period doubling

leading to chaos with chaotic regimes separated by coherent period doubling is often a

fractal structure. We discuss such a fractal in the next chapter and fractals in other con-

texts later in Chapter 14. The existence of this kind of sequential bifurcating behaviour

in such model equations is of considerable potential importance in its biomedical im-

plications: see, for example, the book edited by Othmer et al. (1993), most chapters of

which deal with real medical and physiological examples of oscillatory phenomena.

1.6 Harvesting a Single Natural Population

It is clearly necessary to develop an ecologically acceptable strategy for harvesting any

renewable resource be it animals, ﬁsh, plants, or whatever. We also usually want the

maximum sustainable yield with the minimum effort. The inclusion of economic factors

in population models of renewable resources is increasing and these introduce impor-

tant constraints: see, for example, the seminal books by Clark (1976b, 1985, 1990). The

book by Kot (2001) has a chapter on harvest models and optimal control theory. The re-

view article by Plant and Mangel (1987) is concerned with insect pest management. The

model we describe here is a simple logistic one with the inclusion of a harvesting con-

tribution: it was discussed by Beddington and May (1977). Although it is a particularly

simple one it brings out several interesting and important points which more sophisti-

cated models must also take into account. Rotenberg (1987) also considered the logistic

model with harvesting, with a view to making the model more quantitative. He also

examined the effects of certain stochastic parameters on possible population extinction.

Most species have a growth rate, depending on the population, which more or less

maintains a constant population equal to the environment’s carrying capacity K .That

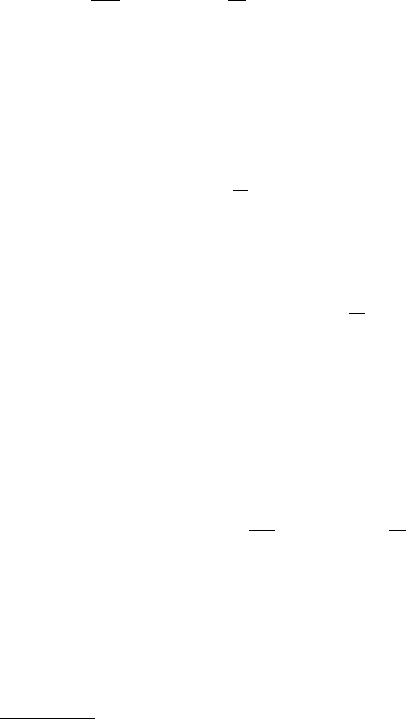
1.6 Harvesting a Single Natural Population 31

is, the growth and death rates are about equal. Harvesting the species affects the mor-

tality rate and, if it is not excessive, the population adjusts and settles down to a new

equilibrium state N

< K . The modelling problem is how to maximise the sustained

yield by determining the population growth dynamics so as to ﬁx the harvesting rate

which keeps the population at its maximum growth rate.

We discuss here a basic model which consists of the logistic population model (1.2)

in which the mortality rate is enhanced, as a result of harvesting, by a term linearly

proportional to N ; namely,

= rN



1 −



− EN = f (N). (1.44)

Here r, K and E are positive constants and EN is the harvesting yield per unit time

with E a measure of the effort expended. K and r are the natural carrying capacity and

the linear per capita growth rate respectively. The new nonzero steady state from (1.44)

(E) = K



1 −



> 0ifE < r (1.45)

which gives a yield

Y (E) = EN

(E) = EK



1 −



. (1.46)

Clearly if the harvesting effort is sufﬁciently large so that it is greater than the linear

growth rate when the population is low, the species will die out. That is, if E > r the

only realistic steady state is N = 0. If E < r (which was possibly not the case, for

example, with whaling in the early 1970’s) the maximum sustained yield and the new

harvesting steady state are, from (1.46) and (1.45),

= Y (E)|

E=r/2

, N

. (1.47)

Does an analysis of the dynamic behavior tell us anything different from the naive, and

often used, steady state analysis just given here?

Figure 1.18 illustrates the growth rate f (N) in (1.44) as a function of N for various

efforts E. Linearising (1.44) about N

(E) gives

(

N − N

)

≈ f



(

(E)

)(

N − N

)

= (E −r)

(

N − N

)

, (1.48)

which shows linear stability if E < r: arrows indicate stability or instability in Fig-

ure 1.18.

We can consider the dynamic aspects of the process by determining the time scale

of the recovery after harvesting. If E = 0 then, from (1.44), the recovery time T =

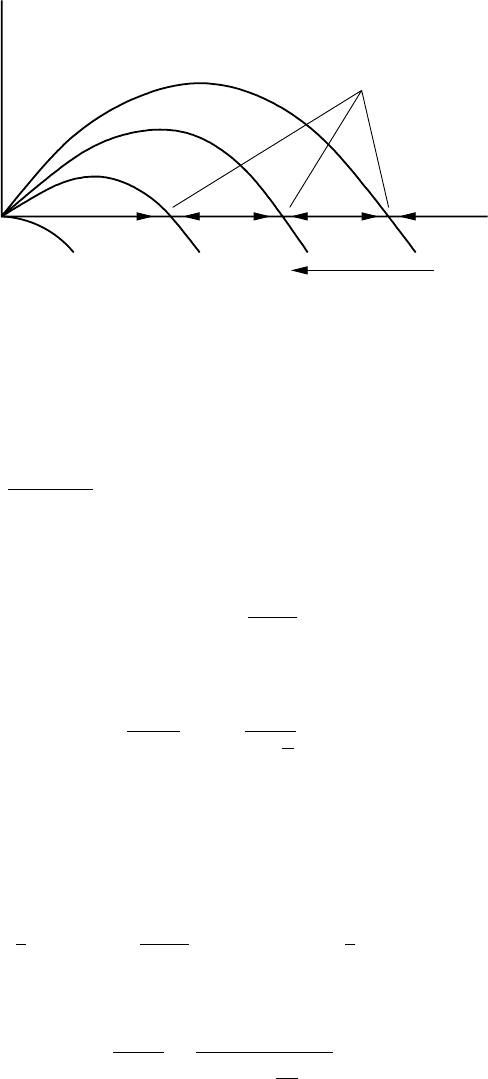
32 1. Continuous Population Models for Single Species

f (N)

E > r

E < r

increasing E

(E)

Figure 1.18. Growth function f (N) for the logistic model with harvesting according to (1.44). Note how the

positive steady state decreases with increasing E, eventually tending to zero as E → r.

O(1/r), namely, the timescale of the reproductive growth. This is the order of magni-

tude of the recovery time of N to its carrying capacity K after a small perturbation from

K since, for N(t) − K small and N

(0) = K, (1.48) shows

d(N − K)

≈−r(N − K ) ⇒ N(t) − K ∝ e

−rt

If E = 0, with 0 < E < r, then the recovery time in a harvesting situation, from (1.48),

(E) = O



r − E



and so

(E)

(0)

= O



1 −



. (1.49)

Thus for a ﬁxed r,alargerE increases the recovery time since T

(E)/T

(0) increases

with E.WhenE = r/2, the value giving the maximum sustained yield Y

, T

(E) =

O(2T

(0)).

The usual deﬁnition of a recovery time is the time to decrease a perturbation from

equilibrium by a factor e. Then, on a linear basis,

(0) =

, T

(E) =

r − E

⇒ T



E =



= 2T

(0). (1.50)

Since it is the yield Y that is recorded, if we solve (1.46) for E in terms of Y we have

(Y )

(0)

1 ±



1 −



1/2

(1.51)

1.6 Harvesting a Single Natural Population 33

(a) (b)

(Y )

(0)

−

Y/Y

K/2 N

(E)

rN(1−N/K )

Y =EN

Y =EK(1−E/r)

=EN

(E)

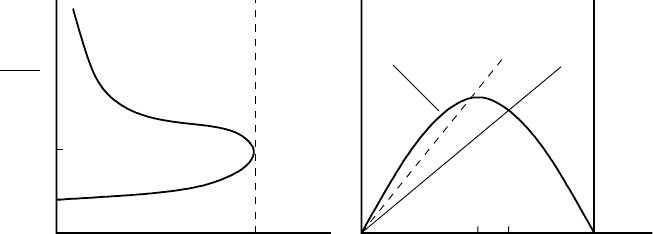
Figure 1.19. (a) Ratio of the recovery times as a function of the yield for the logistic growth model, with

yield proportional to the population: equation (1.44). (b) Graphical method for determining the steady state

yield Y for the harvested logistic model (1.44).

which is sketched in Figure 1.19(a) where L

and L

−

denote the positive and negative

roots of (1.51). It is clearly advantageous to stay on the L

branch and potentially

disastrous to get onto the L

−

one. Let us now see what determines the branch.

Suppose we start harvesting with a small effort E; then, as is clear from Fig-

ure 1.19(b), the equilibrium population N

(E) is close to K and N

(E)>K/2, the

equilibrium population for the maximum yield Y

. The recovery time ratio T

(E)/

(0) from (1.50) is then approximately 1. So increasing E, and hence the yield, we

are on branch L

.AsE increases further, N

(E) decreases towards K /2, the value

for the maximum sustained yield Y

and we reach the point A in Figure 1.19(a) when

(E) = K /2. As E is increased further, N

(E)<K/2 and the recovery time is

further increased but with a decreasing yield; we are now on the L

−

branch.

We can now see what an optimal harvesting strategy could be, at least from this

deterministic point of view. An effort E should be made which keeps the equilibrium

population density N

(E)>K/2, but as close as possible to K /2, the value for the

maximum sustained yield. The closer to K /2, however, the more delicate the situation

becomes since we might inadvertently move onto branch L

−

in Figure 1.19(a). At this

stage, when N

(E) is close to K/2, a stochastic analysis should be carried out; this

was done by Beddington and May (1977). Stochastic elements of course reduce the

predictability of the catch. In fact, with this model, they decrease the average yield for

a given effort.

Before leaving this model, we can see how it is difﬁcult to use models such as these

for determining a maximum yield in practice. Often a maximum yield is only found in

practice when attempts have been made to obtain an even greater yield. If the model

here were valid such a scenario could be catastrophic, since if one moves onto the upper

branch the reduction in effort might not be sufﬁcient to move onto the bottom curve. So

even without a stochastic analysis we can see how random variations could play havoc

with the concept of a maximum sustainable yield.

As an alternative harvesting resource strategy suppose we harvest with a constant

yield Y

as our goal, a model studied by Brauer and Sanchez (1975). The model equation

34 1. Continuous Population Models for Single Species

(a) (b)

rK/4

rN(1 − N/K)

f (N)

increasing

)

Figure 1.20. (a) Equilibrium states for the logistic growth harvested with a constant yield Y

: equation (1.52).

(b)Growthrate f (N ) in (1.52) as the yield Y

increases.

is then

= rN



1 −



−Y

= f (N;r, K, Y

). (1.52)

Figure 1.20(a) shows the graphical way of determining the steady states as Y

varies. It

is trivial to ﬁnd the equilibria analytically of course, but often the behavioural traits

as a parameter varies are more obvious from a ﬁgure, such as here. If 0 < Y

rK/4 = Y

, the maximum sustainable yield here, there are two positive steady states

), N

)>N

) which from Figure 1.20(b) are respectively unstable and sta-

ble. As Y

→ rK/4, the maximum sustainable yield of the previous model is even more

sensitive to ﬂuctuations since if a perturbation from N

takes N to a value N < N

the

mechanism then drives N to zero; see Figure 1.20(b). Not only that, N → 0inaﬁnite

time since for small enough N, (1.52) becomes dN/dt ≈−Y

and so for any starting

at t

, N(t) ≈ N

−Y

(t −t

) and N(t) = 0whent = t

+ N

For easy comparison with the constant effort model we evaluate the equivalent

recovery time ratio T

)/T

(0). The recovery time T

) is only relevant to the

stable equilibrium N

) which from (1.52) is

) =



1 +



1 −



1/2



, Y

< rK/4.

The linearised form of (1.52) is then

d(N − N

))

≈ (N − N

)



∂ f

∂ N



)

=−(N − N

) r



1 −



1/2

1.6 Harvesting a Single Natural Population 35

Thus

)

(0)



1 −



1/2

, Y

(1.53)

which shows that T

)/T

(0) →∞as Y

→ Y

. This model is thus a much more

sensitive one and, as a harvesting strategy, is not really adequate.

One conclusion from this modelling exercise is that a constant effort rather than a

constant yield harvesting strategy is less potentially catastrophic. It also calls into ques-

tion, even with this simple model, the ﬁshing laws, for example, which regulate catches.

A more realistic model, on the lines described here, should take into account the eco-

nomic costs of harvesting and other factors. This implies a feedback mechanism which

can be a stabilising factor; see Clark (1976b, 1985, 1990). With the unpredictability

of the real world it is probably essential to include feedback. Nevertheless such sim-

ple models can pose highly relevant ecological and long term ﬁnancial questions which

have to be considered in any more realistic and more sophisticated model.

The problems of sustainable harvesting of renewable resources are crucially im-

portant, whether it is in ﬁsheries, forestry management or any other renewable resource

which depends on the maintenance of a reproductive surplus in a population. In the

above very simple example we saw how it is possible to move onto a catastrophic path

if we do not have sufﬁcient information such as knowing, a priori, what the maximum

sustainable yield can be. The basic concept of a sustainable resource depends on a re-

productive surplus being maintained under a variety of circumstances many of which

are difﬁcult to quantify. With the difﬁculty of obtaining accurate data it makes it even

more difﬁcult to produce a workable model system on which to base decisions. Ludwig

and his colleagues (Ludwig 1993, 1994, 1995, 1996a, 1996b, Ludwig et al. 1993, 1997

and other references given in these) persuasively argue the case for a more sophisticated

and realistic modelling in which stochastic elements play a crucial role. Numerous real

case studies are discussed which highlight potentially serious problems with overly sim-

ple models. They demonstrate the importance of assessing the possibility of population

extinction because of, among other things, uncertainty about crucial parameters, small

stochastic elements and the effect of rare catastrophes. For anyone seriously considering

working in the ecological ﬁeld of harvesting of renewable resources these papers should

be required reading. The book by Getz and Haight (1989) gives a good survey of the

ﬁeld of population harvesting and resource management in diverse areas. It discusses

numerous mathematical models and applications to speciﬁc case studies for which ﬁeld

data are available. The book edited by Levin (1994, Parts V and VI)) contains arti-

cles which are also particularly relevant. The book by Hilborn and Mangel (1997) is

also relevant: it confronts models with data and discusses numerous practical case stud-

ies which require a probabilistic approach. They provide the necessary statistics and

probability background necessary for the study of the various models. The 1990’s have

witnessed several population collapses of what were hitherto thought of as sustainable

resources, such as cod in the north Atlantic and what looks like being another with

salmon in the north east Paciﬁc coast to mention but two. Sadly even when the scien-

tiﬁc knowledge is available as to a future catastrophe, politics and short term economics

prevent its implementation.