Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

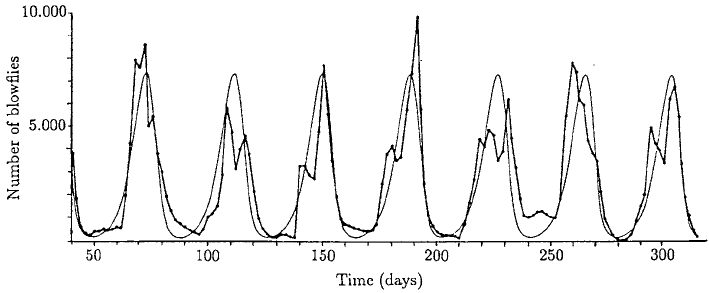
16 1. Continuous Population Models for Single Species

observed the population of ﬂies which were maintained under carefully regulated tem-

perature and food control. He observed a regular basic periodic oscillation of about 35

to 40 days. Applying (1.12) to the experimental arrangement, K is set by the food level

available. T , the delay, is approximately the time for a larva to mature into an adult.

Then the only unknown parameter is r, the intrinsic rate of population increase. Fig-

ure 1.12 illustrates the comparison with the data for rT = 2.1 for which the period

is about 4.54T . If we take the observed period as 40 days this gives a delay of about

9 days; the actual delay is closer to 11 days. The model implies that if K is doubled

nothing changes from a time periodic point of view since it can be scaled out by writing

N/K for N; this lack of change with K is what was observed.

It is encouraging that such a simple model as (1.12) should give such reasonable

results. This is some justiﬁcation for using delay models to study the dynamics of sin-

gle populations which exhibit periodic behaviour. It is important, however, not to be too

easily convinced as to the validity or reasonableness of a model simply because some

solutions agree even quantitatively well with the data; this is a phenomenon, or rather a

pitfall, we encounter repeatedly later in the book particularly when we discuss models

for generating biological pattern and form in Chapter 2 to Chapter 6, Volume II. From

the experimental data reproduced in Figure 1.12 we see a persistent ‘second burst’ fea-

ture that the solutions of (1.12) do not mimic. Also the difference between the calculated

delay of 9 days and the actual 11 days is really too large. Gurney et al. (1980) inves-

tigated this problem with a more elaborate delay model which agrees even better with

the data, including the two bursts of reproductive activity observed; see also the book

by Nisbet and Gurney (1982) where this problem is discussed fully as a case study.

Another example of the application of this model (1.12) to extant data is given

by May (1981) who considers the lemming population in the Churchill area of Canada.

There is approximately a 4-year period where, in this case the gestation time is T = 0.72

year. The vole population in the Scottish Highlands, investigated by Stirzaker (1975)

using a delay equation model, also undergoes a cycle of just under 4 years, which is

again approximately 4T where here the gestation time is T = 0.75 year. In this model

the effect of predation is incorporated into the single equation for the vole population.

Figure 1.12. Comparison of Nicholson’s (1957) experimental data for the population of the Australian sheep-

blowﬂy and the model solution from (1.12) with rT = 2.1. (From May 1975).

1.4 Delay Population Models: Periodic Solutions 17

The article by Myers and Krebs (1974) discusses population cycles in rodents in general:

they usually have 3 to 4 year cycles.

Not all periodic population behaviour can be treated quite so easily. One such ex-

ample which is particularly dramatic is the 13- and 17-year cycle exhibited by a species

of locusts; that is, their emergences are synchronized to 13 or 17 years.

It should perhaps be mentioned here that single (nondelay) differential equation

models for population growth without delay, that is, like dN/dt = f (N), cannot exhibit

limit cycle behaviour. We can see this immediately as follows. Suppose this equation

has a periodic solution with period T ;thatis,N(t + T ) = N(t). Multiply the equation

by dN/dt and integrate from t to t + T to get



t+T





dt =



t+T

f (N)



N(t+T )

N(t)

f (N) dN

= 0

since N(t + T ) = N(t). But the left-hand integral is positive since (dN/dt)

cannot

be identically zero, so we have a contradiction. So, the single scalar equation dN/dt =

f (N) cannot have periodic solutions.

1.4 Linear Analysis of Delay Population Models: Periodic Solutions

We saw in the last section how the delay differential equation model (1.12) was capable

of generating limit cycle periodic solutions. One indication of their existence is if the

steady state is unstable by growing oscillations, although this is certainly not conclusive.

We consider here the linearisation of (1.12) about the equilibrium states N = 0and

N = K . Small perturbations from N = 0 satisfy dN/dt ≈ rN, which shows that

N = 0 is unstable with exponential growth. We thus need only consider perturbations

about the steady state N = K .

It is again expedient to nondimensionalise the model equation (1.12) by writing

∗

(t) =

N(t)

, t

∗

= rt, T

∗

= rT, (1.14)

where the asterisk denotes dimensionless quantities. Then (1.12) becomes, on dropping

the asterisks for notational simplicity, but keeping in mind that we are now dealing with

nondimensional quantities,

dN(t)

= N(t)

[

1 − N(t − T )

]

. (1.15)

Linearising about the steady state, N = 1, by writing

18 1. Continuous Population Models for Single Species

N(t) = 1 +n(t) ⇒

dn(t)

≈−n(t − T ). (1.16)

We look for solutions for n(t) in the form

n(t) = ce

λt

⇒ λ =−e

−λT

, (1.17)

from (1.16), where c is a constant and the eigenvalues λ are solutions of the second of

(1.17), a transcendental equation in which T > 0.

It is not easy to ﬁnd the analytical solutions of (1.17). However, all we really want

to know from a stability point of view is whether there are any solutions with Re λ>0

which from the ﬁrst of (1.17) implies instability since in this case n(t) grows exponen-

tially with time.

Set λ = µ + iω. There is a real number µ

such that all solutions λ of the second

of (1.17) satisfy Re λ<µ

. To see this take the modulus to get |λ |=e

−µT

and so, if

|λ |→∞then e

−µT

→∞which requires µ →−∞. Thus there must be a number

that bounds Re λ from above. If we introduce z = 1/λ and w(z) = 1 +ze

−T/z

then

w(z) has an essential singularity at z = 0. So by Picard’s theorem, in the neighbourhood

of z = 0,w(z) = 0 has inﬁnitely many complex roots. Thus there are inﬁnitely many

roots λ.

We now take the real and imaginary parts of the transcendental equation in (1.17),

namely,

µ =−e

−µT

cos ωT,ω= e

−µT

sin ωT, (1.18)

and determine the range of T such that µ<0. That is, we want to ﬁnd the conditions

such that the upper limit µ

on µ is negative. Let us ﬁrst dispense with the simple case

where λ isreal;thatis,ω = 0. From (1.18), ω = 0 satisﬁes the second equation and the

ﬁrst becomes µ =−e

−µT

. This has no positive roots µ>0sincee

−µT

> 0forallµT

or as can be seen on sketching each side of the equation as a function of µ and noting

that they can only intersect with T > 0ifµ<0.

Consider now ω = 0. From (1.18) if ω is a solution then so is −ω, so we can

consider ω>0 without any loss of generality. From the ﬁrst of (1.18), µ<0 requires

ωT <π/2since−e

−µT

< 0forallµT . In principle (1.18) deﬁnes µ(T ), ω(T ).

We are interested in the value of T when µ(T ) ﬁrst crosses from µ<0toµ>0.

As T increases from zero µ = 0ﬁrstwhenωT = π/2. From (1.18) we see that if

µ = 0 the second equation gives as the only relevant solution ω = 1 occurring at

T = π/2. Since this is the ﬁrst zero of µ as T increases, this gives the bifurcating value

T = T

= π/2. Another way of deriving this is to show, from (1.18), that the gradient

of µ(T )at µ = 0, namely, (∂µ/∂T )

T =π/2

> 0. Anticipating the result of the following

analysis that ω<1forT >π/2, note in passing that (∂ω/∂T )

T =π/2

< 0. So we have

0 < T <

(1.19)

as the condition on T for stability.

1.4 Delay Population Models: Periodic Solutions 19

Returning now to dimensional quantities we thus have that the steady state N(t) =

K is stable if 0 < rT <π/2 and unstable for rT >π/2. In the latter case we expect

the solution to exhibit stable limit cycle behaviour. The critical value rT = π/2isthe

bifurcation value, that is, the value of the parameter, rT here, where the character of the

solutions of (1.12) changes abruptly, or bifurcates, from a stable steady state to a time-

varying solution. The effect of delay in models is usually to increase the potential for

instability. Here as T is increased beyond the bifurcation value T

= π/2r, the steady

state becomes unstable.

Near the bifurcation value we can get a ﬁrst estimate of the period of the bifurcating

oscillatory solution as follows. Consider the dimensionless form (1.15) and let

T = T

+ε =

+ε, 0 <ε 1. (1.20)

The solution λ = µ + iω, of (1.18), with the largest Re λ when T = π/2isµ = 0,

ω = 1. For ε small we expect µ and ω to differ from µ = 0andω = 1alsobysmall

quantities so let

µ = δ, ω = 1 +σ, 0 <δ 1, |σ |1, (1.21)

where δ and σ are to be determined. Substituting these into the second of (1.18) and

expanding for small δ, σ and ε gives

1 +σ = exp



−δ



+ε



sin



(

1 +σ

)



+ε



⇒ σ ≈−

πδ

to ﬁrst order, while the ﬁrst of (1.18) gives

δ =−exp



−δ



+ε



cos



(

1 +σ

)



+ε



⇒ δ ≈ ε +

πσ

Thus on solving these simultaneously

δ ≈

1 +

,σ≈−

επ



1 +



, (1.22)

and hence, near the bifurcation, the ﬁrst of (1.17) with (1.16) gives

N(t) = 1 +Re {c exp [δt +i(1 +σ)t]}

≈ 1 +Re



c exp



εt

1 +



exp





1 −

επ

2(1 +



(1.23)

This shows that the instability is by growing oscillations with period

2π

1 −

επ

2(1+

)

≈ 2π

20 1. Continuous Population Models for Single Species

to O(1) for small ε.Indimensional termsthisis2π/r and, since to O(1), rT = π/2,

the period of oscillation is then 4T as we expected from the intuitive arguments above.

From the numerical results for limit cycles quoted above the solution with rT = 1.6

had period 4.03T . With rT = π/2 + ε = 1.6, this gives ε ≈ 0.029 so the dimensional

period to O(ε) is obtained from the last equation as

2π

1 −

επ





≈ 4.05T,

which compares well with the numerical computed value of 4.03T .WhenrT = 2.1

this gives ε ≈ 0.53 and corresponding period 5.26T which is to be compared with the

computed period of 4.54T .Thisε is too large for the above ﬁrst order analysis to hold

(ε

is not negligible compared with ε); a more accurate result would be obtained if the

analysis were carried out to second order.

The natural appearance of a ‘slow time’ εt in N(t) in (1.23) suggests that a full

nonlinear solution near the bifurcation value rT = π/2 is amenable to a two-time

asymptotic procedure to obtain the (uniformly valid in time) solution. This can in fact be

done; see, for example, Murray’s (1984) book on asymptotic methods for a pedagogical

description of such techniques and how to use them.

The subject of delay or functional differential equations is now rather large. An

introductory mathematical book on the subject is Driver’s (1977). The book by Mac-

Donald (1979) is solely concerned with time lags in biological models. Although the

qualitative properties of such delay equation models for population growth dynamics

and nonlinear analytical solutions near bifurcation can often be determined, in general

numerical methods have to be used to get useful quantitative results.

A very useful technique for determining the necessary conditions for stability of

the solutions of linear delay equations is given by van den Driessche and Zou (1998)

and which we now give: it is a Liapunov function technique (for example, Jordan and

Smith 1999) which gives an estimate for the stability parameter space. Equation (1.16)

above is a special case of the general equation

= ay(t) + by(t −τ), t > 0, (1.24)

where τ is the delay and a and b are constant parameters. We could, of course, carry out

an equivalent analysis as we did on (1.16) and get the necessary and sufﬁcient conditions

for stability and thereby determine the parameter space where the steady state is stable.

If y

is a steady state L[y(t)] is a Liapunov function if L[y(t)] > 0forally(t) = y

L[y(t)]=0fory(t) = y

(that is, L positive deﬁnite) and dL[y(t)]/dt < 0forall

y(t) = y

. If such a function can be found then y

is globally asymptotically stable

and no closed solution orbits are possible. Such a Liapunov function can be found for

(1.24); it is given by

L[y(t)]=y

(t) +|b |



t−τ

(s) ds, (1.25)

where y(t) is a solution of (1.24).

1.5 Delay Models in Physiology: Periodic Dynamic Diseases 21

We have to show that it is indeed a Liapunov function. Certainly L > 0forall

y = 0andL = 0wheny(t) = y

= 0. Furthermore

= 2y(t)

+|b |[y

(t) − y

(t − τ)]

= 2ay

(t) +2|b |y(t)y(t − τ) +|b |[y

(t) − y

(t −τ)]

≤ 2ay

(t) +|b |[y

(t) + y

(t − τ)]+|b |[y

(t) − y

(t −τ)]

= 2(a +|b |)y

(t)

≤ 0, for a < −|b |.

(1.26)

So, L[y(t)] satisﬁes all the conditions of a Liapunov function and so the steady state

= 0 is globally stable for all a < −|b | which gives the parameter space where

y = 0 is stable—and not just linearly stable. If a full stability analysis is carried out as

we did for (1.16) the stability domain is actually larger but not markedly so; they are

both, however, of the same broad general shape.

1.5 Delay Models in Physiology: Periodic Dynamic Diseases

There are many acute physiological diseases where the initial symptoms are manifested

by an alteration or irregularity in a control system which is normally periodic, or by

the onset of an oscillation in a hitherto nonoscillatory process. Such physiological peri-

odic diseases have been termed dynamical diseases by Glass and Mackey (1979) who

have made a particular study of several important physiological examples. The sym-

posium proceedings of a meeting speciﬁcally devoted to temporal disorders in human

oscillatory systems edited by Rensing et al. (1987) is particularly apposite to the ma-

terial and modelling in this section, as is the nontechnical intuitive book by Glass and

Mackey (1988) (which has many applications) and that edited by Othmer et al. (1993).

Other examples are discussed by Mackey and Milton (1990) and Milton and Mackey

(1989). Here we discuss two speciﬁc examples which have been modelled, analysed and

related to experimental observations by Mackey and Glass (1977). The review article

on dynamic diseases by Mackey and Milton (1988) is of direct relevance to the mate-

rial discussed here; it also describes some examples drawn from neurophysiology. The

book by Keener and Sneyd (1998) has other examples. Although the second model we

consider is concerned with populations of cells, the ﬁrst does not relate to any popula-

tion species but rather to the concentration of a gas. It does, however, ﬁt naturally here

since it is a scalar delay differential equation model the analysis for which is directly

applicable to the second problem. It is also interesting in its own right.

Cheyne–Stokes Respiration

The ﬁrst example, Cheyne–Stokes respiration, is a human respiratory ailment mani-

fested by an alteration in the regular breathing pattern. Here the amplitude of the breath-

ing pattern, directly related to the breath volume—the ventilation V —regularly waxes

and wanes with each period separated by periods of apnea, that is where the volume per

22 1. Continuous Population Models for Single Species

Figure 1.13. A spirogram of the breathing pattern of a 29-year-old man with Cheyne–Stokes respiration. The

typical waxing and waning of the volume of breath is interspersed with periods of low ventilation levels; this

is apneic breathing. (Redrawn with permission from Mackey and Glass 1977)

breath is exceedingly low. Figure 1.13 is typical of spirograms of those suffering from

Cheyne–Stokes respiration.

We ﬁrst need a few physiological facts for our model. The level of arterial carbon

dioxide (CO

), c(t) say, is monitored by receptors which in turn determine the level of

ventilation. It is believed that these CO

-sensitive receptors are situated in the brainstem

so there is an inherent time lag, T say, in the overall control system for breathing levels.

It is known that the ventilation response curve to CO

is sigmoidal in form. We assume

the dependence of the ventilation V on c to be adequately described by what is called a

Hill function, of the form

V = V

max

(t − T )

, (1.27)

where V

max

is the maximum ventilation possible and the parameter a and the Hill co-

efﬁcient m are positive constants which are determined from experimental data. (We

discuss the biological relevance of Hill functions and how they arise later in Chapter 6.)

We assume the removal of CO

from the blood is proportional to the product of the

ventilation and the level of CO

in the blood.

Let p be the constant production rate of CO

in the body. The dynamics of the CO

level is then modelled by

dc(t)

= p −bVc(t) = p −bV

max

c(t)

(t − T )

, (1.28)

where b is a positive parameter which is also determined from experimental data. The

delay time T is the time between the oxygenation of the blood in the lungs and moni-

toring by the chemoreceptors in the brainstem. This ﬁrst order differential-delay model

exhibits, as we shall see, the qualitative features of both normal and abnormal breathing.

As a ﬁrst step in analysing (1.28) we introduce the nondimensional quantities

x =

, t

∗

, T

∗

,α=

abV

max

, V

∗

max

(1.29)

1.5 Delay Models in Physiology: Periodic Dynamic Diseases 23

and the model equation becomes



(t) = 1 −αx(t)

(t − T )

1 + x

(t − T )

= 1 −αxV

(

x(t − T )

)

, (1.30)

where for notational simplicity we have omitted the asterisks on t and T .

As before we get an indication of the dynamic behaviour of solutions by investigat-

ing the linear stability of the steady state x

given from (1.30) by

1 = α

m+1

1 + x

= αx

(

)

= αx

, (1.31)

where V

, deﬁned by the last equation, is the dimensionless steady state ventilation.

A simple plot of 1/αx

and V (x

) as functions of x

shows there is a unique positive

steady state. If we now consider small perturbations about the steady state x

we write

u = x − x

and consider |u | small. Substituting into (1.30) and retaining only linear

terms we get, using (1.31),



=−αV

u − αx



u(t − T ), (1.32)

where V



= dV(x

)/dx

is positive. As in the last section we look for solutions in the

form

u(t) ∝ e

λt

⇒ λ =−αV

−αx



−λT

. (1.33)

If the solution λ with the largest real part is negative, then the steady state is stable.

Since here we are concerned with the oscillatory nature of the disease we are interested

in parameter ranges where the steady state is unstable and, in particular, unstable by

growing oscillations in anticipation of limit cycle behaviour. So, as before, we must

determine the bifurcation values of the parameters such that Re λ = 0.

Set λ = µ + iω. In the same way as in the last section it is easy to show that a

real number µ

exists such that for all solutions λ of (1.33), Re λ<µ

and also that

no real positive solution exists. For notational simplicity let us write the transcendental

equation (1.33) as

λ =−A − Be

−λT

, A = αV

> 0, B = αx



> 0. (1.34)

Equating real and imaginary parts gives

µ =−A − Be

−µT

cos ωT,ω= Be

−µT

sin ωT. (1.35)

Simultaneous solutions of these give µ and ω in terms of A, B and T : we cannot de-

termine them explicitly of course as we saw in Section 1.4. The bifurcation we are

interested in is when µ = 0 so we consider the parameter ranges which admit such a

solution. With µ = 0 the last equations give, with s = ωT ,

24 1. Continuous Population Models for Single Species

cot s =−

, ⇒

< s

<π (1.36)

for all ﬁnite AT > 0wheres

is a solution. We can see that such a solution s

exists

on sketching cot s and −AT/s as functions of s. There are of course other solutions

of this equation in the ranges [(2m + 1)π/2,(m + 1)π] for m = 1, 2,... but we

need only consider the smallest positive solution s

since that gives the bifurcation for

the smallest critical T > 0. We now have to determine the parameter ranges so that

with µ = 0ands

substituted back into (1.35) a solution exists. That is, what are the

restrictions on A, B and T so that

0 =−A − B cos s

, s

= BT sin s

are consistent? These imply

BT =



(

)



1/2

. (1.37)

If B, A and T , which determine s

, are such that the last equality cannot hold then no

solution with µ = 0 exists.

Since A and B are positive, the solution is stable in the limiting case T = 0since

then Re λ = µ =−A − B < 0. Now consider (1.35) and increase T from T = 0. From

the last equation and (1.36) a solution with µ = 0 cannot exist if

BT <



(

)



1/2

cot s

=−AT,

< s

<π

(1.38)

and, from continuity arguments from T = 0wemusthaveµ<0. So the bifurcation

condition which just gives µ = 0 is (1.37). Or, put in another way, if (1.38) holds, the

steady state solution of (1.30) is linearly, and in fact globally, stable. In terms of the

original dimensionless variables from (1.34) the conditions are thus

αx



T <



(

αV

)



1/2

cot s

=−αV

(1.39)

If we now have A and B ﬁxed, a bifurcation value T

is given by the ﬁrst of (1.38) with

an equality sign in the inequality.

Actual parameter values for normal humans have been obtained by Mackey and

Glass (1977). The concentration of gas in blood is measured in terms of the partial

pressure it sustains and so it is measured in mmHg (that is, in torr). Relevant to the

dimensional system (1.28), they estimated

= 40 mmHg p = 6 mmHg/min, V

= 7 litre/min,



= 4 litre/min mmHg, T = 0.25 min.

(1.40)

1.5 Delay Models in Physiology: Periodic Dynamic Diseases 25

From (1.31), which deﬁnes the dimensionless steady state, we have αV

= 1/x

.So,

with (1.39) in mind, we have, using (1.40) and the nondimensionalisation (1.29),

αV

T =

dimensional

= 0.0375.

The solution of the second of (1.39) with such a small right-hand side is s

≈ π/2and

so s

 αV

T which means that the inequality for stability from the ﬁrst of (1.39) is

approximately, but quite accurately,



2αx

. (1.41)

So, if the gradient of the ventilation at the steady state becomes too large the steady

state becomes unstable and limit cycle periodic behaviour ensues. With the values in

(1.40) the critical dimensional V



= 7.44 litre/min mmHg. The gradient increases with

the Hill coefﬁcient m in (1.27). Other parameters can of course also initiate periodic

behaviour; all we require is that (1.41) is violated.

In dimensional terms we can determine values for m and a in the expression (1.27)

for the ventilation, which result in instability by using (1.41) with (1.29) and V

from

(1.31). Figures 1.14(a) and (b) show the dimensional results of numerical simulations

of (1.28) with two values for V



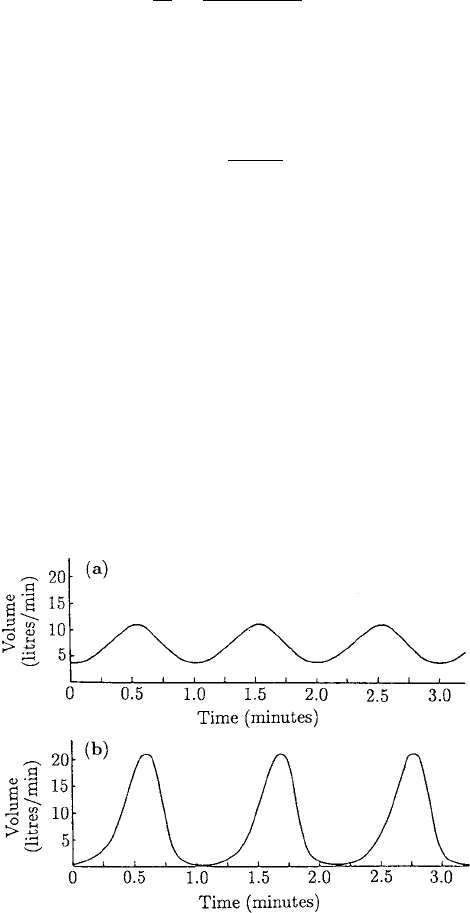
Note that the period of oscillation in both solutions in Figure 1.14 is about 1 minute,

which is 4T where T = 0.25 min is the estimate for delay given in (1.40). This is as we

would now expect from the analysis in the last section. A perturbation analysis in the

vicinity of the bifurcation state in a similar way to that given in the last section shows

Figure 1.14. (a) The solution behaviour of the model equation (1.30) presented in dimensional terms for



= 7.7 litre/min mmHg. (b) The solution behaviour for V



= 10.01 litre/min mmHg. Note the pronounced

apneic regions, that is where the ventilation is very low: this should be compared with the spirogram in

Figure 1.10. (Redrawn from Glass and Mackey 1979).