Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

xx Contents, Volume II

2.9 Nonexistence of Spatial Patterns in Reaction Diffusion Systems:

General and Particular Results

3. Animal Coat Patterns and Other Practical Applications of Reaction

Diffusion Mechanisms

3.1 Mammalian Coat Patterns—‘How the Leopard Got Its Spots’

3.2 Teratologies: Examples of Animal Coat Pattern Abnormalities

3.3 A Pattern Formation Mechanism for Butterﬂy Wing Patterns

3.4 Modelling Hair Patterns in a Whorl in Acetabularia

4. Pattern Formation on Growing Domains: Alligators and Snakes

4.1 Stripe Pattern Formation in the Alligator: Experiments

4.2 Modelling Concepts: Determining the Time of Stripe Formation

4.3 Stripes and Shadow Stripes on the Alligator

4.4 Spatial Patterning of Teeth Primordia in the Alligator:

Background and Relevance

4.5 Biology of Tooth Initiation

4.6 Modelling Tooth Primordium Initiation: Background

4.7 Model Mechanism for Alligator Teeth Patterning

4.8 Results and Comparison with Experimental Data

4.9 Prediction Experiments

4.10 Concluding Remarks on Alligator Tooth Spatial Patterning

4.11 Pigmentation Pattern Formation on Snakes

4.12 Cell-Chemotaxis Model Mechanism

4.13 Simple and Complex Snake Pattern Elements

4.14 Propagating Pattern Generation with the Cell-Chemotaxis System

5. Bacterial Patterns and Chemotaxis

5.1 Background and Experimental Results

5.2 Model Mechanism for E. coli in the Semi-Solid Experiments

5.3 Liquid Phase Model: Intuitive Analysis of Pattern Formation

5.4 Interpretation of the Analytical Results and Numerical Solutions

5.5 Semi-Solid Phase Model Mechanism for S. typhimurium

5.6 Linear Analysis of the Basic Semi-Solid Model

5.7 Brief Outline and Results of the Nonlinear Analysis

5.8 Simulation Results, Parameter Spaces, Basic Patterns

5.9 Numerical Results with Initial Conditions from the Experiments

5.10 Swarm Ring Patterns with the Semi-Solid Phase Model Mechanism

5.11 Branching Patterns in Bacillus subtilis

6. Mechanical Theory for Generating Pattern and Form in Development

6.1 Introduction, Motivation and Background Biology

6.2 Mechanical Model for Mesenchymal Morphogenesis

6.3 Linear Analysis, Dispersion Relation and Pattern

Formation Potential

Contents, Volume II xxi

6.4 Simple Mechanical Models Which Generate Spatial Patterns with

Complex Dispersion Relations

6.5 Periodic Patterns of Feather Germs

6.6 Cartilage Condensation in Limb Morphogenesis

and Morphogenetic Rules

6.7 Embryonic Fingerprint Formation

6.8 Mechanochemical Model for the Epidermis

6.9 Formation of Microvilli

6.10 Complex Pattern Formation and Tissue Interaction Models

7. Evolution, Morphogenetic Laws, Developmental Constraints and

Teratologies

7.1 Evolution and Morphogenesis

7.2 Evolution and Morphogenetic Rules in Cartilage Formation in the

Vertebrate Limb

7.3 Teratologies (Monsters)

7.4 Developmental Constraints, Morphogenetic Rules and

the Consequences for Evolution

8. A Mechanical Theory of Vascular Network Formation

8.1 Biological Background and Motivation

8.2 Cell–Extracellular Matrix Interactions for Vasculogenesis

8.3 Parameter Values

8.4 Analysis of the Model Equations

8.5 Network Patterns: Numerical Simulations and Conclusions

9. Epidermal Wound Healing

9.1 Brief History of Wound Healing

9.2 Biological Background: Epidermal Wounds

9.3 Model for Epidermal Wound Healing

9.4 Nondimensional Form, Linear Stability and Parameter Values

9.5 Numerical Solution for the Epidermal Wound Repair Model

9.6 Travelling Wave Solutions for the Epidermal Model

9.7 Clinical Implications of the Epidermal Wound Model

9.8 Mechanisms of Epidermal Repair in Embryos

9.9 Actin Alignment in Embryonic Wounds: A Mechanical Model

9.10 Mechanical Model with Stress Alignment of the Actin

Filaments in Two Dimensions

10. Dermal Wound Healing

10.1 Background and Motivation—General and Biological

10.2 Logic of Wound Healing and Initial Models

10.3 Brief Review of Subsequent Developments

10.4 Model for Fibroblast-Driven Wound Healing: Residual Strain and

Tissue Remodelling

xxii Contents, Volume II

10.5 Solutions of the Model Equation Solutions and Comparison with

Experiment

10.6 Wound Healing Model of Cook (1995)

10.7 Matrix Secretion and Degradation

10.8 Cell Movement in an Oriented Environment

10.9 Model System for Dermal Wound Healing with Tissue Structure

10.10 One-Dimensional Model for the Structure of Pathological Scars

10.11 Open Problems in Wound Healing

10.12 Concluding Remarks on Wound Healing

11. Growth and Control of Brain Tumours

11.1 Medical Background

11.2 Basic Mathematical Model of Glioma Growth and Invasion

11.3 Tumour Spread In Vitro: Parameter Estimation

11.4 Tumour Invasion in the Rat Brain

11.5 Tumour Invasion in the Human Brain

11.6 Modelling Treatment Scenarios: General Comments

11.7 Modelling Tumour Resection (Removal) in Homogeneous Tissue

11.8 Analytical Solution for Tumour Recurrence After Resection

11.9 Modelling Surgical Resection with Brain Tissue Heterogeneity

11.10 Modelling the Effect of Chemotherapy on Tumour Growth

11.11 Modeling Tumour Polyclonality and Cell Mutation

12. Neural Models of Pattern Formation

12.1 Spatial Patterning in Neural Firing with a

Simple Activation–Inhibition Model

12.2 A Mechanism for Stripe Formation in the Visual Cortex

12.3 A Model for the Brain Mechanism Underlying Visual

Hallucination Patterns

12.4 Neural Activity Model for Shell Patterns

12.5 Shamanism and Rock Art

13. Geographic Spread and Control of Epidemics

13.1 Simple Model for the Spatial Spread of an Epidemic

13.2 Spread of the Black Death in Europe 1347–1350

13.3 Brief History of Rabies: Facts and Myths

13.4 The Spatial Spread of Rabies Among Foxes I: Background and

Simple Model

13.5 Spatial Spread of Rabies Among Foxes II:

Three-Species (SIR) Model

13.6 Control Strategy Based on Wave Propagation into a

Non-epidemic Region: Estimate of Width of a Rabies Barrier

13.7 Analytic Approximation for the Width of the Rabies

Control Break

Contents, Volume II xxiii

13.8 Two-Dimensional Epizootic Fronts and Effects of Variable Fox

Densitics: Quantitative Predictions for a Rabies Outbreak

in England

13.9 Effect of Fox Immunity on Spatial Spread of Rabies

14. Wolf Territoriality, Wolf–Deer Interaction and Survival

14.1 Introduction and Wolf Ecology

14.2 Models for Wolf Pack Territory Formation: Single Pack—Home Range

Model

14.3 Multi-Wolf Pack Territorial Model

14.4 Wolf–Deer Predator–Prey Model

14.5 Concluding Remarks on Wolf Territoriality and Deer Survival

14.6 Coyote Home Range Patterns

14.7 Chippewa and Sioux Intertribal Conﬂict c1750–1850

Appendix

A. General Results for the Laplacian Operator in Bounded Domains

Bibliography

Index

This page intentionally left blank

1. Continuous Population Models for

Single Species

The increasing study of realistic and practically useful mathematical models in popula-

tion biology, whether we are dealing with a human population with or without its age

distribution, population of an endangered species, bacterial or viral growth and so on, is

a reﬂection of their use in helping to understand the dynamic processes involved and in

making practical predictions. The study of population change has a very long history:

in 1202 an exercise in an arithmetic book written by Leonardo of Pisa involved building

a mathematical model for a growing rabbit population; we discuss it later in Chapter 2.

Ecology, basically the study of the interrelationship between species and their environ-

ment, in such areas as predator–prey and competition interactions, renewable resource

management, evolution of pesticide resistant strains, ecological and genetically engi-

neered control of pests, multi-species societies, plant–herbivore systems and so on is

now an enormous ﬁeld. The continually expanding list of applications is extensive as

are the number of books on various aspects

of the ﬁeld. There are also highly prac-

tical applications of single-species models in the biomedical sciences; in Section 1.5

we discuss two examples of these which arise in physiology. Here, and in the follow-

ing three chapters, we consider some deterministic models by way of an introduction

to the ﬁeld. The excellent books by Hastings (1997) and Kot (2001) are speciﬁcally

on ecological modelling. Elementary introductions are also given in the textbooks by

Edelstein-Keshet (1988) and Hoppensteadt and Peskin (1992).

1.1 Continuous Growth Models

Single-species models are of relevance to laboratory studies in particular but, in the real

world, can reﬂect a telescoping of effects which inﬂuence the population dynamics. Let

N(t) be the population of the species at time t, then the rate of change

= births − deaths +migration, (1.1)

Kingsland (1995) gives a fascinating historical and highly readable account of some of the major ideas

introduced in the 20th century and of some of the scientists involved together with vignettes on how their

egos, often inﬂated, affected the progress of the ﬁeld.

2 1. Continuous Population Models for Single Species

Table 1.1.

Mid 17th Early 19th

Date Century Century 1918–1927 1960 1974 1987 2000 2050 2100

Population

in billions 0.5 1 2 3 4 5 6.3 10 11.2

is a conservation equation for the population. The form of the various terms on the right-

hand side of (1.1) necessitates modelling the situation with which we are concerned. The

simplest model has no migration and the birth and death terms are proportional to N .

That is,

= bN − dN ⇒ N(t) = N

(b−d)t

where b, d are positive constants and the initial population N(0) = N

. Thus if b > d

the population grows exponentially while if b < d it dies out. This approach, due to

Malthus

in 1798, is fairly unrealistic. However, if we consider the past and predicted

growth estimates for the total world population from the 17th to 21st centuries it is

perhaps less unrealistic, as seen in Table 1.1 (United Nations median projections for the

21st century). Since 1900 it has grown exponentially.

Notwithstanding such growth, many demographers now fret about whether or not

there will be enough people in the future! In 1975 about 18% of the world population

lived in countries where the fertility rate was at or below replacement level (approxi-

mately 2.1 children per woman) while in 1997 it was 44% with 67% predicted (United

Nations) by 2015. Later in Chapter 4 we discuss in detail how to calculate a survival

reproductive level. In 1970 there were 10 countries below replacement fertility levels

while by 1995 there were 51 and by 2015 it is estimated that 88 of the approximately

180 countries in the world will join the group with less than replacement fertility. To

mark the 20th anniversary of the World Health Organisation their report (1992) on hu-

man reproduction gave some interesting estimates for the world, such as 100 million

acts of sexual intercourse every day which resulted in 910,000 conceptions and 356,000

cases of sexually transmitted diseases. They estimate that 300 million couples do not

want any more children but lack family planning services. Of the 910,000 conceptions

every day about half are unplanned. There are 150,000 abortions every day, a third in

unsafe conditions resulting in 500 deaths.

One of the reasons for this digression is to highlight the problems of modelling such

population problems. It is difﬁcult to make long term, or even relatively short term,

predictions unless we know sufﬁcient facts to incorporate in the model to make it a

reliable predictor although general trends can in themselves be useful even if ultimately

Malthus’ essay, ﬁrst published anonymously, was immensely inﬂuential (on Charles Darwin, for example,

who ﬁrst read it in 1838), but also roused much wrath in various quarters for much of the following century. He

said in effect that unbounded population growth would be controlled by war, pestilence or famine. After the

carnage of the First World War his predictions were again brought to the fore and widely discussed. Malthus,

who married at 38, spent much of his life as an English country parson who, by all accounts, was a happy

family man who thoroughly enjoyed life.

1.1 Continuous Growth Models 3

quantitatively wrong. There is no doubt, however, that, in spite of widespread available

contraception, sterilisation being the most commonly used method (female sterilisation

accounting for 26% of the total with male sterilisation accounting for 10%), enforced

size of families, local famines, new diseases, increasing nonreplacement fertility rates

and so on, the world population continues to increase alarmingly.

In the long run of course there must be some adjustment to such exponential growth.

Verhulst (1838, 1845) proposed that a self-limiting process should operate when a pop-

ulation becomes too large. He suggested

= rN(1 − N/K ), (1.2)

where r and K are positive constants. This he called logistic growth in a population. In

this model the per capita birth rate is r(1 − N/K ); that is, it is dependent on N.The

constant K is the carrying capacity of the environment, which is usually determined by

the available sustaining resources.

There are two steady states or equilibrium states for (1.2), namely, N = 0andN =

K,thatis,wheredN/dt = 0. N = 0 is unstable since linearization about it (that is,

is neglected compared with N)givesdN/dt ≈ rN,andsoN grows exponentially

from any small initial value. The other equilibrium N = K is stable: linearization about

it (that is, (N − K)

is neglected compared with | N − K |)givesd(N − K )/dt ≈

−r(N − K ) and so N → K as t →∞. The carrying capacity K determines the

size of the stable steady state population while r is a measure of the rate at which it is

reached; that is, it is a measure of the dynamics: we could incorporate it in the time by

a transformation from t to rt. Thus 1/r is a representative timescale of the response of

the model to any change in the population.

If N(0) = N

the solution of (1.2) is

N(t) =



K + N

(

−1

)



→ K as t →∞, (1.3)

and is illustrated in Figure 1.1. From (1.2), if N

< K, N(t) simply increases mono-

tonically to K while if N

> K it decreases monotonically to K . In the former case

there is a qualitative difference depending on whether N

> K/2orN

< K/2; with

< K/2 the form has a typical sigmoid character, which is commonly observed.

In the case where N

> K this would imply that the per capita birth rate is negative!

Of course all it is really saying is that in (1.1) the births plus immigration are less than

the deaths plus emigration. The point about (1.2) is that it is more like a metaphor for

a class of population models with density-dependent regulatory mechanisms—a kind

of compensating effect of overcrowding—and must not be taken too literally as the

equation governing the population dynamics. In spite of its limitations, from time to

time, it has been rediscovered and widely hyped as some universal law of population

growth.

One example is in the 1925 book by the biologist Pearl (1925). Kingsland

(1995) describes the episode in fascinating detail: Pearl toured the country pushing his

As late as 1985 I heard it put forward, with missionary zeal, as a universal law by Dr. Jonas Salk (of polio

vaccine renown) in a major lecture he gave at the University of Utah.

4 1. Continuous Population Models for Single Species

t, time

N(t)

Figure 1.1. Logistic population growth. Note the qualitative difference for the two cases N

< K/2and

K > N

> K/2.

theory. He certainly conﬁrmed Charles Darwin’s maxim: ‘Great is the power of steady

misinterpretation.’ The main point about the logistic form is that it is a particularly

convenient form to take when seeking qualitative dynamic behaviour in populations

in which N = 0 is an unstable steady state and N(t) tends to a ﬁnite positive stable

steady state. The logistic form will occur in a variety of different contexts throughout the

book primarily because of its algebraic simplicity and because it provides a preliminary

qualitative idea of what can occur with more realistic forms.

It is instructive to try to understand why the logistic form was accepted since it high-

lights an important point in modelling in the biomedical sciences. The logistic growth

form in (1.3) has three parameters, N

, K and r with which to assign to compare with

actual data. These were used by Pearl (1925) to ﬁt the census population data for various

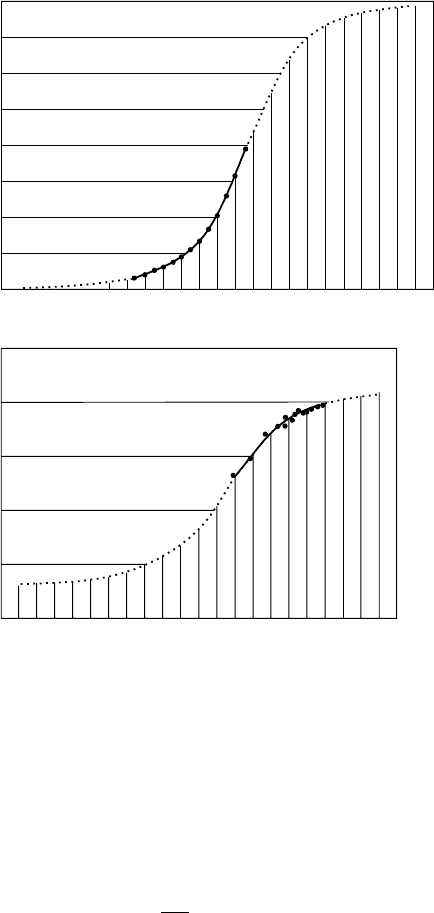
countries including the United States, Sweden and France for various periods. Figure 1.2

shows the results for France and the U.S. If we look at the U.S. data there is a good ﬁt

for the population roughly from 1790 until about 1910; here the lower part of the curve

is ﬁtted. However, the rest of the curve is nowhere near the actual population data. The

same holds for France but the data were ﬁtted to the upper part of the curve but even

there the subsequent population growth prediction is wrong. The main point is not that

the predictions are so inaccurate but rather that curve ﬁtting only part of the data, and

particularly the part which does not cover the major part of the growth curve makes

comparison with data and future predictions extremely unreliable. Of course, we could

produce an algebraic expression with a few more parameters (and derive some differ-

ential equation for which it is the solution) and do a better job but then all we would be

doing would be curve ﬁtting without increasing our understanding of the actual mech-

anism governing the phenomenon. The motivation for modelling such as we discuss in

this book is to further our understanding of the underlying processes since it is only in

this way that we can make justiﬁable predictions.

1.1 Continuous Growth Models 5

50 50 50 50 507525 25 25 25 2575 75 75 751500 1600 1700 1800 1900 2000

POPULATION IN MILLIONS

France

YEAR

(b)

YEAR

(a)

1700 604020 80 1800 21002000190020 20 2040 40 4060 60 6080 80 80

POPULATION IN MILLIONS

200

175

150

125

100

U.S.

asymptote ≈197

asymptote ≈0

asymptote ≈42.6

asymptote ≈6.6

Figure 1.2. Logistic population growth (1.3) used to ﬁt the census data for the population of (a)theU.S.and

(b) France. The data determine the parameters only over a small part of the growth curve. (Redrawn from

Pearl 1925)

In general if we consider a population to be governed by

= f (N), (1.4)

where typically f (N) is a nonlinear function of N then the equilibrium solutions N

∗

are solutions of f (N ) = 0 and are linearly stable to small perturbations if f



∗

)<0,

and unstable if f



∗

)>0. This is clear from linearising about N

∗

by writing

n(t) ≈ N(t) − N

∗

, |n(t) |1