Морозов В.Г., Фетисов Ю.К. Молекулярная физика. Курс физики. Часть 1
Подождите немного. Документ загружается.


Q < 0
A
η =
Q
A
,
Q ≥ 0
η
η = 1
p
V T U
p = p(V, T ), U = U(V, T ).
p =
M
µ
RT
V
,
U =
i
2
M
µ
RT.

p V T U
p V
V p p T
V T
C
1
(p
1
, V
1
) C
2
(p
2
, V
2
)
p V
p = p(V )
p V
V
V
1
V
2
dV
p
p
1
p
2
C
1
C
2
0
δA = p dV
1 → 2
A
1→2
=
V
2
Z
V
1
p(V ) dV.
V
1
C
1
C
2
V
2
A
1→2
p = p(V )
C
1
C
2
V = const
p = const T = const
T
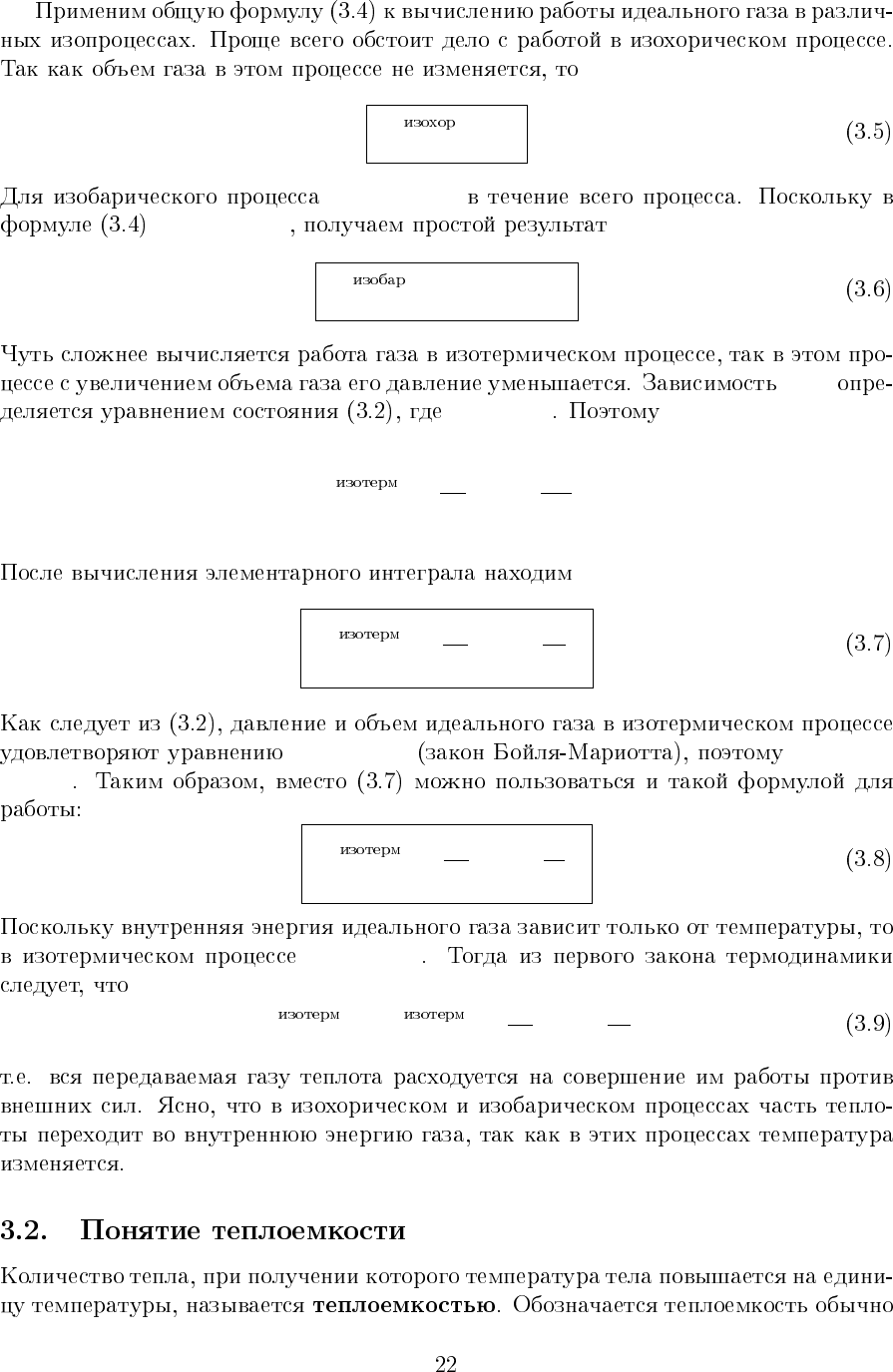
A
( )
1→2
= 0.
p = p
1
= p
2
p(V ) = const
A
( )
1→2
= p (V
2
− V
1
) .
p(V )
T = const
A
( )
1→2
=
M
µ
RT
V
2
Z
V
1
dV
V
.
A
( )
1→2
=
M
µ
RT ln
V
2
V
1
.
pV = const (V
2
/V
1
) =
(p
1
/p
2
)
A
( )
1→2
=
M
µ
RT ln
p
1
p
2
.
U = const
Q
( )
1→2
= A
( )
1→2
=
M
µ
RT ln
V
2
V
1
,

C
δQ T T + dT
C =
δQ
dT
.
0 ∞
δQ = 0
C = 0
dT = 0 T = const
δQ
1
T
1
T
1
+ dT
δQ
2
T
2
T
2
+ dT
C
v
C
p
C
v
=
δQ
dT
V
, C
p
=
δQ
dT
p
.
V p
δA = 0
δQ = dU
C
v
=
∂U
∂T
V
.
C
v
U = U(V, T ) f(x, y)
x y (∂f/∂x)
y
x
y
(∂f/∂y)
x

C
p
c
/ ·
/ ·
C
v
C
p
V
C
v
C
v
=
i
2
R.
C
p
dV
dT
δQ = dU + p dV,
δQ
dU dV
p = const dT
(δQ/dT )
p
C
p
=
∂U
∂T
p
+ p
∂V
∂T
p
.
∂U
∂T
p
=
∂U
∂T
V
= C
v
.
ν = M/µ C C = νC
C

V = RT/p (∂V/∂T )
p
= R/p
C
p
= C
v
+ R ,
C
v
C
p
=
i + 2
2
R.
γ =
C
p
C
v
.
γ =
i + 2
i
.
γ
γ
i
i = 3
γ = 5/3 ≈ 1, 667
n = 3
n = 2
n = 1
i = 7 γ = 9/7 ≈ 1, 286

T,
o
C γ
H
2
O
2
Br
2
I
2
NH
3
C
2
H
6
γ
1, 667
γ 1, 286 I
2
Br
2
γ
H
2
O
2
HI γ
H
2
O
2
HI
i = 5 γ = 7/5 = 1, 4
H
2
O
2
HI I
2
γ
γ = 1, 286
NH
3
4 × 3 = 12
i = 18 γ = 20/18 ≈ 1, 11
γ = 1, 31
γ = 8/6 ≈ 1, 333

γ
i > 3 γ 1, 667
i γ
kT
E
n
= (n + 1/2)~ω n = 0, 1, 2, . . .
ω
~ = h/2π = 1, 05 · 10
−34
· h
2π n = 0 E
0
∆E = ~ω
∆E
ω
(3/2)kT
T kT ~ω
kT ~ω

kT
ω
T
v
=
~ω
k
T ≥ T
v
T T
v
T
v
≈ 6000
H
2
T
r
r
T
v
T
r
≈ 175
T
r
T 0 T
r
T
v
3R/2
5R/2
7R/2
C
v
C
p
C
v
v

V p T
δQ = 0
δA = −dU.
δA
δA
A
( )
1→2
= U
1
− U
2
,
U
1
U
2
U = U(T ) = C
v
T
A
( )
1→2
= C
v
(T
1
− T
2
)
A
( )
1→2
> 0 T
2
< T
1
A
( )
1→2
< 0 T
2
> T
1
δA = p dV
p dV + C
v
dT = 0.
p
ν = M/µ
p = RT/V
C
v
T R/C
v
γ − 1
(γ − 1)
dV
V
+
dT
T
= 0,
