Морозов А.В. Домашняя работа по алгебре за 7 класс
Подождите немного. Документ загружается.

181
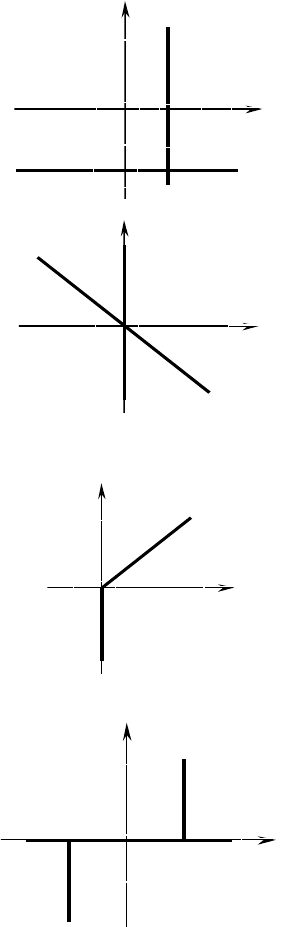
№1257.
а) (x – 20)(y + 3) = 0; x = 2; y = – 3.
x
y
O
2
−
3
б) x
2
+ xy = 0, x(y + x) = 0, x = 0; y = – x.
x
y
O
№1258.
а) y + ⎮y⎮ = x; при 0≥y ⎮y⎮ = y; y = 0,5x;
при y < 0 ⎮y⎮ = –y; x = 0.
x
y
O
б) y = x⎮y⎮; при y < 0 ⎮y⎮ = y; x = 1;
при y < 0 ⎮y⎮ = –y; x = –1. при y = 0 x = ⎯ любое.
x
y
O
182
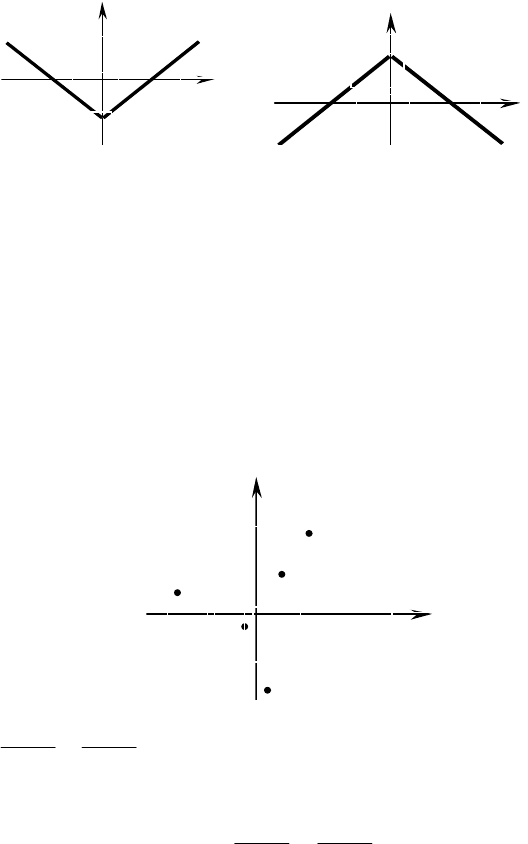
№1259.
а) y = ⎮x⎮ – 3; б) y = 4 – ⎮x⎮;
⎩
⎨
⎧
<−−
≥−
=
.0 при ,3
0 при ,3
xx
xx
y
⎩
⎨
⎧
<+
≥−
=
.0 при ,4
0 при ,4
xx
xx
y
x
y
O
−
3
x
y
O
4
№1260.
Поиск этого числа будем проводить следующим образом: выпишем квад-
раты всех четных чисел от 2 до 20: 4; 16; 36; 64; 100; 144; 196; 256; 324; 400.
После разделим эти числа на 2: 2; 8; 18; 32; 50; 72; 98; 128; 162; 200. Полу-
ченные числа умножим на 3 (если среди результатов найдется куб нату-
рального числа, то соответсвующее число из второго дейсвия и будет реше-
нием): 6; 24; 54; 96; 150; 216; 294; 384; 486; 600. Число 216 есть 6
2
, т.е.
искомое число 72. Ответ: 72.
№1261.
Число 96 заканчивается цифрой 6, а, значит, 96
7
заканчивается цифрой 6.
Число 22 заканчивается цифрой 2, а, значит, 25
5
заканчивается цифрой 2.
Число 48 заканчивается цифрой 8 = 2
3
, а, значит, последняя цифра числа 48
6
совпадает с 8
6
= 2
18
= (2
9
)
2
= 512
2
. Т.к число 512 заканчивается на 2, то 512
2
заканчивается на 4. 6 – 2 – 450, а, значит, число 96
7
– 22
5
– 48
6
заканчивает-
ся цифрой 0, т.е. делится на 10.
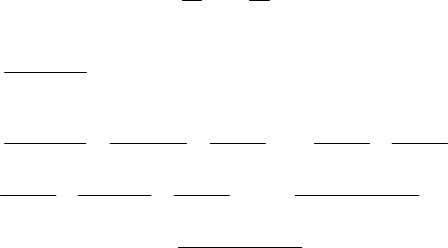
№1262.
M
A
С
B
D
x
y
O
№1263.
10
11
10 1
10 1
+
+
?
11
12
10 1
10 1
;
+
+
⏐(10
11
+ 1)(10
12
+ 1);
(10
10 +
1)(10
12 +
1) ? (10
11 +
1)
2
; 10
22 +
10
10 +
10
12 +
1 ? 10
22 +
2⋅10
11 +
1;
10
10 +
10
12
? 2⋅10
11
; 10
10 +
10⋅10
11
? 2⋅10
11
;
10
10
>0, 10⋅10
11
>2⋅10
11
, значит,
10
11
10 1
10 1
+
+
>
11
12
10 1
10 1
+
+
.
183
№1264.
2x
2
+ 2y
2
= x
2
+ 2xy + y
2
+ x
2
– 2xy + y
2
= (x + y)
2
+ (x – y)
2
.
№1265.
5a
2
– 6ab + 5b
2
= 5a
2
– 10ab + 5b
2
+ 4ab = 5(a – b)
2
+ 4ab.
а) Рассмотрим выражение 5a
2
– 6ab + 5b
2
. Пусть ab<0 (т.е. a и b разных зна-
ков). Тогда 5a
2
>0, –6ab>0, 5b
2
>0, значит, 5a
2
– 6ab + 5b
2
>0.
б) Рассмотрим выражение 5(a – b)
2
+ 4ab. Пусть ab>0 (т.е. a и b одного зна-
ка). Тогда 5(a – b)
2
>0, 4ab>0, значит, 5(a – b)
2
+ 4ab>0.
Учитывая, что два рассмотренных равенства тождественно равны, получа-
ем 5a
2
– 6ab + 5b
2
>0, если a ≠ 0 или b ≠ 0.
№1266.
(x –3)(x–5)+2 = x
2
– 3x –5x + 25 + 2 = x
2
– 8x + 16 +11 = (x – 4)
2
+ 11.
Т.к.
0)4(
2
≥−x , 11> 0, то (x –4
2
) + 11> 0.
№1267.
а) x
8
+ x
4
–2 = (x
8
–1) +(x
4
–1) = (x
4
–1)(x
4
+ 1) + (x
4
– 1) = (x
4
–1)(x
4
+ 1 + 1) =
= (x
4
+2)(x
4
– 1).
б) a
5
– a
2
– a – 1 = (a
5
–a) – (a
2
+1) = a(a
4
–1) – (a
2
+ 1) = a(a
2
+ 1)(a
2
– 1) –
– (a
2
+1) = (a
2
+ 1)(a
3
–a –1).
в) n
4
+ 4 = n
4
+ 4n
2
+ 4 – 4n
2
= (n
2
+2) – (2n)
2
= (n
2
+2n +2)( n
2
–2n +2).
г) n
4
+ n
2
+ 1 = n
4
+2n
2
+ 1 – n
2
= (n
2
+ 1)
2
– n
2
= (n
2
+ n +1)(n
2
–n +1).
№1268.
p – 1 = (p – 1)(p +1).
Простое число p всегда нечетное, если p>3. Отсюда следует, что
(p – 1) и (p + 1) последовательные четные числа, причем одно из них делит-
ся на 4. Значит, (p – 1)(p +1) кратно 2 ⋅ 4 = 8. Рассмотрим 4 числа (p – 1), p и
(p + 1). Одно из них всегда делится на 3, но p ⎯ простое и p>3,
значит либо
(p – 1), либо (p + 1) кратно 3. Значит, (p – 1)(p +1) кратно 8 ⋅ 3 = 24. Отсюда
получаем, что p
2
– 1 делится на 24.
№1269.
Пусть наши числа a – 2; a – 1; a; a + 1; 3≥a .
(a – 2)
2
+ (a – 1)
2
+ a
2
+ (a + 1)
2
+ (a + 2)
2
= a
2
– 4a + 4 + a
2
–2a + 1 + a
2
+ a
2
+
+ 2a + 1 + a
2
+ 4a + 4 = 5a
2
+ 10.
1) Пусть a ⎯ четное, тогда a
2
= 4n, где n ⎯ некоторое натуральное число.
5a
2
+ 10 = 20n +10 = 10(2n +1) = 5(4n + 2) = 2(10n +5).
Мы представили 5a
2
+ 10 в виде произведения двух натуральных чисел. В
любом из трех случаев одно из них четное, а другое нечетное. Значит, если
a ⎯ четное число, то 5a
2
+ 10 не есть квадрат некоторого натурального
числа.
2) Пусть a ⎯ нечетное, тогда a
2
= 2n + 1, где n ⎯ некоторое натуральное
число. 5a
2
+ 10 = 10k + 15 = 5(2k + 3).
Мы представили 5a
2
+ 10 в виде произведения двух натуральных чисел.
Значит 2n + 3 = 5, n = 1. 5a
2
+ 10 = 25; 5a
2
= 15; a
2
= 3.
Натурального числа, квадрат которого равен трем, не существует, следова-
тельно, если a ⎯ нечетное число, то 5a
2
+ 10 не есть квадрат некоторого
натурального числа.
184
3) Если a ⎯ натуральное число, не четное, не нечетное одновременно, то
сумма квадратов пяти последовательных натуральных чисел не квадрат на-
турального числа.
№1270.
Пусть a ⎯ число не кратное трем. a
2
– 1 = (a – 1)( a + 1).
Т.к. a не кратно 3, то либо (a – 1), либо (a+1) кратно 3, значит a
2
– 1 кратно
трем.
№1271.
(2 + 1)(2
2
+ 1)(2
4
+ 1)(2
8
+ 1)(2
16
+ 1)(2
32
+ 1) =
= (2 – 1)(2 + 1)(2
2
+ 1)(2
4
+ 1)(2
8
+ 1)(2
16
+ 1)(2
32
+ 1) = 2
64
– 1
№1272.
x
2
– y
2
= 30.
Рассмотрим
0≥x , 0≥y из – за того, что x
2
= ( – x)
2
, y
2
= ( – y)
2
.
1) Пусть x = 2n, y = 2k. x
2
– y
2
= 4(n
2
– k
2
) = 30; 2(n
2
– k
2
) = 15.
Четное число равно нечетному, чего быть не может.
2) Пусть x = 2n + 1, y = 2k + 1.
x
2
– y
2
= (2n + 1)
2
– (2k + 1)
2
= 4(n
2
+ n – k
2
– k) = 30; 2(n
2
+ n – k
2
– k) = 15.
Четное число равно нечетному, чего быть не может.
3) Пусть x = 2n + 1, y = 2k.
x
2
– y
2
= (2n + 1)
2
– 4k
2
= 4n
2
+ 4n + 1 – 4k
2
= 4(n
2
+ n – k
2
) + 1 = 30.
4(n
2
+ n – k
2
) = 29.
Четное число равно нечетному, чего быть не может.
4) Пусть x = 2n, y = 2k + 1;
x
2
– y
2
= 4n
2
– (2k + 1)
2
= 4n
2
– 4k
2
– 4k – 1 = 4(n
2
– k
2
– k) = 31.
Четное число равно нечетному, чего быть не может.
Значит, уравнение x
2
– y
2
= 30 не имеет целых корней.
№1273.
a ⋅ 19
3
+ b ⋅ 19
2
+ с ⋅ 19 + d = 1; a ⋅ 62
3
+ b ⋅ 62
2
+ с ⋅ 62 + d = 2;
Пусть a, b, с, d ⎯ целые числа. Условия a = 0 и b = 0 не могут быть выпол-
нены одновременно, т.к. решения системы
{
19 1
62 2
cd ;
cd ;
+=
+=
есть числа
1
43
c,=
24
43
d,=
т.е. не целые. Значит, можно вы-
разить из первого уравнения 19
2
(19a + b) = 1 − d − 19c, а из второго
2
262
62
62
dc
.
ab
−−
=
+
Преобразуем последнюю формулу:
2
262
62
62
dc
ab
−−
==
+
119
62
dc
ab
−−
+
+
143
62
c
ab
−
=
+
2
19
19
62
ab
ab
+
+
+
143
62
c
ab
−
=
+
2
62
19
62
ab
ab
+
=−
+
2
43 19
62
a
ab
⋅⋅
+
+
143
62
c
ab
−
=
+
19
2
+
2
143(19 )
62
ac
.
ab
−⋅+
+
Отсюда следует:
2
22
143(19 )
62 19
62
ac
.
ab
−⋅+
−=
+
62
2
− 19
2
= (62 − 19)(62 + 19) = 43 ⋅ 81.

185
Значит, получаем:
2
143(19 )
43 81
62
ac
.
ab
−⋅+
⋅=
+
Таким образом
2
2
143(19 ) 1
81(62 ) (19 ).
43 43
ac
ab ac
−⋅+
+= = − ⋅+
Перенесем скобку в левую часть равенства:
81(62a + b) + (19
2
⋅ a + c) =
1
43
.
Мы нашли, что с помощью операций сложения и умножения на число над
целыми числами получено дробное число, чего быть не может. Значит, та-
ких коэффициентов a, b, с, d не существует.
№1274.
2
x
z
y
+
=
.
x
4
+2x
3
z−2xz
3
−z
4
−4x
2
y
2
+4y
2
z
2
=x
4
+2x
3
z − 2xz
3
− z
4
− x
2
(x + z)
2
+ z
2
x + z
2
=
= x
4
+ 2x
3
z − 2xz
3
− z
4
− x
2
(x
2
+ 2xz + z
2
)+ z
2
(z
2
+ 2xz + x
2
) =
x
4
+ 2x
3
z − 2xz
3
− x
4
− 2x
3
z − z
2
x
2
+ x
2
z
2
+ 2xz
3
+ z
4
= 0.
№1275.
p
2
+2q
2
= 1; 2q
2
= p
2
-1; 2q
2
= (p-1)(p+1).
p≠2, т.к. четное число не может быть равно нечетному.
1) При p>2 p — нечетное, значит, (p-1)(p+1) — четные, причемодно из них
делится на 4. Т.е. (p-1)(p+1) кратно 8. Значит 2p
2
кратно 8. Отсюда следует,
что q = 2. 8 = p
2
– 1; p
2
= 9; p = 3.
№1276.
5x
3
– 32x
2
+ 75x – 71 = a(x – 2)
3
+ b(x – 2)
2
+ d
Пусть y = x – 2, тогда x = y + 2.
ay
3
+ by
2
+ cy + d = 5(y + 2)
3
– 32(y + 2)
2
+ 75(y + 2) – 71 =
= 5(y
3
+ 6y
2
+ 12y + 8) – 32(y
2
+ 4y + 4) + 75(y + 2) – 71 =
= 5y
3
+30y
2
+60y+40–32y
2
–128y–128+75y+150–71 = 5y
3
– 2y
2
+ 7y – 9.
Ответ: a = 5; b = – 2; c = 7; d = – 7.
№1277.
y = x + 1 ⇒ x = y – 1.
3x
3
+ 7x
2
+ 9x + 6 = 3(y – 1)
3
+ 7(y – 1)
2
+ 9(y – 1) + 6 =
= 3(y
3
– 3y
2
+ 3y – 1) + 7(y
2
– 2y + 1) + 9(y – 1) + 6 =
= 3y
2
– 9y
2
+ 9y – 3 + 7y
2
– 14y + 7 + 9y – 9 + 6 = 3y
3
– 2y
2
– 4y + 1.
Ответ: a = 3; b = – 2; c = – 4; d = 1.
№1278.
Т. к. x, y –натуральные, то y может быть равнятся 1,2.
1) Пусть y = 1. 3x + 7y = 3x + 7 = 23; 3x = 16;
x =
3
16
– не натуральное число.
2) Пусть y = 2. 3x + 7y = 3x + 14 = 23; 3x = 9; x = 3.
Ответ: (3,2).
186
№1279.
а)
1
1
8
x
y;
yz ;
zx ;
−=−
⎧
⎪
−
=−
⎨
+=
⎪
⎩
{
2
8
x
z;
zx ;
−=−
+=
; 2x = 6; x = 3;
3 – y = – 1; y = 4; z + 3 = 8; z = 5. Ответ: (3;4;5).
б)
3
6
1
x
y;
yz ;
zx ;
+=−
⎧
⎪
+=
⎨
+=
⎪
⎩
3
6
1
x
y;
yz ;
zx ;
+=−
⎧
⎪
−−=−
⎨
+=
⎪
⎩
{
9
1
x
z;
zx ;
−
=−
+=
2x = – 8; x = – 4;
– 4 + y = – 3; y = 1; z – 4 = 1; z = 5; Ответ: ( – 4;1;5).
№1280.
Пользуясь таблицами на форзацах книги, находим, что это число
729 = 27
2
= 9
3
. Других таких чисел нет. Ответ: 729.
№1281.
Пусть a и b искомые числа. Т. к. их наибольший общий делитель 24 , то a =
24n, b = 24k, где n и k взаимно простые числа.
a + b = 24n + 24k = 24(n + k); 24(n + k) = 168; n + k = 7;
Значит, возможны случаи: n=1 и k=6; n=2 и k=5; n=3 и k=4; n=4 и k=3; n=5
и
k = 2; n = 6 и k = 1. a = 24; b = 144; a = 48; b = 120; a = 72; b = 96; a = 96;
b = 72; a = 120; b = 48; a = 144; b = 24.
№1282.
x + z = 26; x = 3 и y = 23; x = 23 и y = 3;
x = 7 и y = 19; x = 19 и y = 7; x = 13 и y = 13.
№1283.
1ч 7мин = 67мин; 1ч 16мин = 76мин; 18км/ч =
18км
60с
= 0,3км/мин.
По ровной дороге мотоциклист ехал
12
40мин.
03
,
=
Значит в гору и под гору
он ехал туда 67 – 40 = 27мин, обратно 76 – 40 = 36мин.
В гору Под гору
S,км t, мин
v,
мин
км
S, км t, мин
v,
мин
км
Туда 3 x
1
1
3
x
6 y
1
1
6
y
Обратно 6 x
2
2
6
x
3 y
2
2
3
y
11
22
12
12
27
36
36
63
x
y;
x
y;
;
xx
;
yy
+=
⎧
⎪
+=
⎪
⎪
=
⎨
⎪
⎪
=
⎪
⎩
27
11
36
22
2
21
1
2
2
x
y;
x
y;
xx;
y
y;
+=
⎧
⎪
+=
⎪
=
⎨
⎪
⎪
=
⎩
11
1
1
27
236
2
x
y;
y
x
;
+=
⎧
⎪
⎨
+=
⎪
⎩
{
11
11
27
472
xy ;
x
y;
+=
−−=−
187
– 3x
1
= – 45; x
1
= 15; y
1
= 27 – 15 = 12.
Значит, туда в гору мотоциклист ехал 15мин = 0,25ч, под гору 12мин = 0,2ч.
1
1
33
12км/ч
025
v
x,
== =
,
2
1
66
30км/ч
02
v
y,
== = .
Ответ: 12км/ч; 30км/ч.
№1284.
Пусть сейчас x лет брату, y лет сестре.
{
22( 2);
85( 8);
xy
xy
−= −
−= −
{
22 4
8540
xy;
x
y;
−= −
−+ =− +
6 = – 3y + 36; 3y = 30; y = 16.
Значит сестре 10 лет.
x = 2(y – 2) + 2 = 2(10 – 2) + 2 = 18. Значит, брату 18 лет.
Ответ: 18 лет, 10 лет.
№1285.
Пусть x ⎯ скорость автобуса, y ⎯ скорость автомобиля. Реально они ехали
1ч 30 мин = 90 мин. Если бы автобус выехал на 1ч 15 мин раньше, то он бы
ехал 90 – 15 + 75 =150 мин; Если бы автомобиль выехал на 15 мин позже, то
он бы ехал 90 – 15 – 15 = 60 мин.
{
90 90 180
150 60 180
x
y;
x
y;
+=
+=
2 ( 2)
52 6
xy ;
xy;
⎧+ = ⋅−
⎨
+=
⎩
{
22 4
52 6
x
y;
x
y;
−
−=−
+=
3x = 2; x =
3
2
; y = 2 − x = 2 −
3
2
= .
3
4
Значит, скорость автобуса
2
3
км/мин =
2
3
⋅
60 км
ч
= 40 км / час, скорость ав-
томобиля
4
3
км/мин =
4
3
⋅
60 км
ч
= 80 км / час.
Ответ: 40 км/час; 80 км/час.
№1286.
Пусть x ⎯ скорость велосипедиста, y ⎯скорость второго автобуса; значит,
скорость первого автобуса 1
5
7
y =
12
7
y. С первым автобусом велосипедист
встретился через 1ч 20 мин = 1
1
3
ч =
4
3
ч, со вторым через 2 ч.
4412
100 3 7
337
2 2 100
x
y;
xy ;
⎧
⎪
+⋅ = ⋅⋅
⎨
⎪
+=
⎩
{
28 48 2100
2 2 100
x
y;
xy ;
+=
+=
7 12 525
50 ( 12)
xy ;
xy ;
+=
⎧
⎨
+= ⋅−
⎩
{
7 12 525
12 12 600
xy ;
x
y;
+=
−− =−
− 5x = −75; x = 15.
Значит, скорость велосипедиста 15 км/час.
Ответ: 15 км/час.
№1287.
Пусть s ⎯расстояние между пунктами A и B, x
⎯
скорость всадника, у ⎯
скорость пешехода. Всадник двигался 1ч 40 мин = 100 мин.
188
2 100 ;
50 ;
22
;
sx
s
s
x
y
ss
x
y
⎧
⎪
=
⎪
⎪
+=
⎨
⎪
+−
⎪
=
⎪
⎩
50;
50 50 ;
22
;
s
x
s
y
ss
x
xyy
⎧
=
⎪
⎪
⎪
+=
⎨
⎪
⎪
+=−
⎪
⎩
50;
100;
22
50 100 ;
s
x
s
y
x
y
⎧
=
⎪
⎪
⎪
=
⎨
⎪
⎪
+= −
⎪
⎩
150
;
1 100
;
11
25;
xs
ys
xy
⎧
=
⎪
⎪
⎪
=
⎨
⎪
⎪
+=
⎪
⎩
50 100
25;
ss
+=
50 + 100 = 25s; s =6; x = 6; x = ;
50
6
50
=
s
6
100 100
s
y;==
Значит, расстояние между A и B 6 км,
скорость всадника
6
50
км/мин =
660 км
50 ч
⋅
= 7,2 км/ч,
скорость пешехода
6
100
км/мин =
660 км
100 ч
⋅
= 3,6 км/ч.
Ответ: 6 км; 7,2 км/ч; 3,6 км/ч.
№1288.
1) Тонна только что добытого угля содержит сухой массы
1т⋅
100 2
098 т
100
%%
,
%
−
=
.
2) Пусть x ⎯ масса угля после двух недель пребывания на воздухе. Тогда
масса воды в угле с одной стороны равна х ⎯ 0,98, с другой
12
012
100
%
x
,x.
%
⋅=
x − 0,98 = 0,12х; 0,88х = 0,98; x =
49
44
.
Значит, масса угля
49
44
т. Масса воды в угле
49 49 49 49 1 1 49 25 22 147
098 т.
44 44 50 2 22 25 2 550 1100
,
⎛−
⎞
− =−= − =⋅ =
⎜
⎟
⎠
⎝
Ответ:
147
1100
т.
№1289.
Пусть х ⎯ скорость ходьбы братьев, s ⎯ расстояние от школы до дома, y ⎯
скорость бега, t ⎯ время, которое первый брат бегал.
15
2
615 ;
215;
2
x
s
xt
s
t
xx
x
tty x
⎧
−−
⎪
⎪
+= ++
⎨
⎪
=−⋅
⎪
⎩
615 15 ;
2
30 ;
2
t
t
t
xty
⎧
=
+− −
⎪
⎪
⎨
⎛⎞
⎪
+=
⎜⎟
⎪
⎝⎠
⎩
12;
30
2
;
t
t
y
xt
=
⎧
⎪
+
⎨
⎪
=
⎩
12
30
6
3
12
y
x
+
=
= .
Значит, скорость бега в 3 раза больше скорости ходьбы.
Ответ: 3.
189
