Морозов А.В. Домашняя работа по алгебре за 7 класс
Подождите немного. Документ загружается.

141
№1105.
x + 2x = 18, 3x = 18, x = 6. Ответ: (3; 3).
№1106.
Подставим x и y в уравнение: a⋅2 + 2 ⋅ 1 = 8, 2a + 2 = 8, 2a = 6, a = 3.
Т.е. 3x + 2y = 8.
№1107.
а) 2c(c – 4)
2
– c
2
(2c – 10) = 2c(c
2
– 8c + 16) – 2c
3
+ 10c
2
=
= 2c
3
– 16c
2
+ 32c – 2c
3
+ 10c
2
= –6c
2
+ 32c = 2c(–3c + 16);
при c = 0,2, 2c(–3c + 16) = 2 ⋅ 0,2(–3 ⋅ 0,2 + 16) = 0,4 ⋅ 15,4 = 6,16
б) (a – 4b)(4b + a) = a
2
– 16b
2
;
при a = 1,2; b = –0,6, a
2
– 16b
2
= 1,44 – 16 ⋅ 0,36 = 1,44 – 5,76 = –4,32.
№1108.
а) 1+a–a
2
– a
3
= (1 + a) – a
2
(1 + a) = (1 – a
2
)(1 + a)=(1–a)(1 + a)(1 + a);
б) 8–b
3
+4b–2b
2
=(2–b)(4+2b + b
2
) + 2b(2 – b)=(2–b)(4 + 2b + b
2
+ 2b) =
= (2 – b)(4 + 4b + b
2
) = (2 – b)(2 + b)
2
= (2 – b)(2 + b)(2 + b).
40. График линейного уравнения с двумя переменными
№1109.
3x + 4y = 12;
а) A(4; 1), т.к. 3 ⋅ 4 + 4 ⋅ 1 = 12 + 4 = 16 ≠ 12 , то A ∉ графику;
б) B(1; 3), т.к. 3 ⋅ 1 + 4 ⋅ 3 = 3 + 12 = 15 ≠ 12 , то B ∉ графику;
в) C(–6; –7,5), т.к. 3 ⋅ (–6) + 4 ⋅ (–7,5) = –48 ≠ 12 , то C ∉ графику;
г) D(0; 3), т.к. 3 ⋅ 0 + 4 ⋅ 3 = 12, то D ∈ графику.
№1110.
x – 2y = 4;
а) A(6; 1), т.к. 6 – 2 ⋅ 1 = 4, то A ∈ графику;
б) B(–6; –5), т.к. –6 – 2 ⋅ (–5) = 4 , то B ∈ графику;
в) C(0; –3), т.к. 0 – 2 ⋅ (–2) = 4, то C ∈ графику;
г) D(–1; 3), т.к. –1 – 2 ⋅ 3 = –7 ≠ 4, то D ∉ графику.
№1111.
3x – y = –5, т.к. 3 ⋅ (–1) – 2 = –5, то P ∈ графику;
–x + 10y = 21, т.к. –(–1) + 10 ⋅ 2 = 21, то P ∈ графику;
11x + 21y = 31, т.к. 11 ⋅ (–1) + 21 ⋅ 2 = 31, то P ∈ графику.
№1112.
а) 2x – y = 6
y = 2x – 6
x 0 3
y –6 0
–
6
3
x
y
0
y
= 2
x
–6
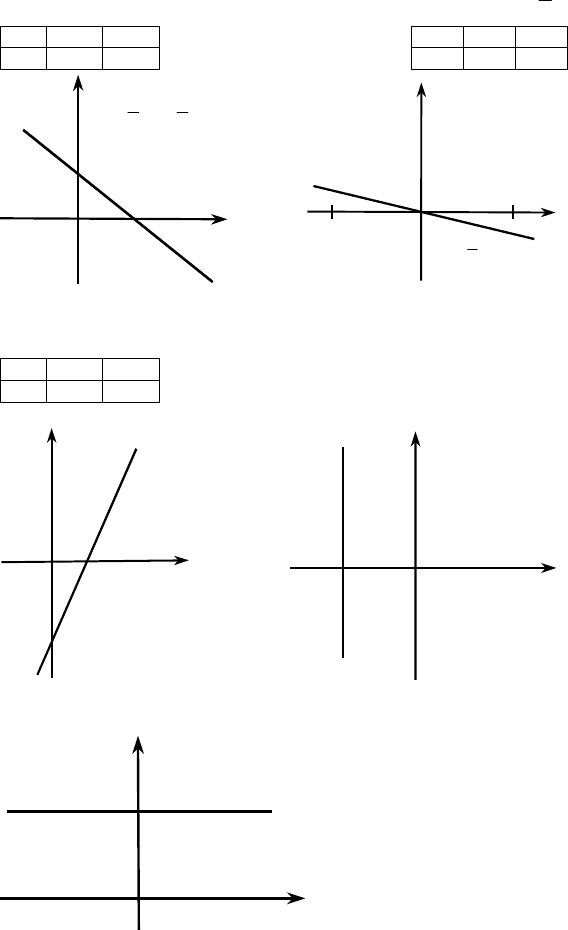
142
б) 1,5x + 2y = 3, y = –0,75x + 1,5; в) x + 6y = 0, 6y = –x, y = –
6
1
x;
x 0 2 x 0 6
y 1,5 0 y 0 –1
y
= –
4
3
x
+
2
1
1
1
,
5
2
x
y
0
–
6
y
= –
6
1
x
x
y
0
6
г) 0,5y – x = –1, 0,5y = x – 1, д)1,2x = –4,8, x = –4;
y = 2x – 2;
x 0 1
y –2 0
y
= 2
x
– 2
x
y
0
x
= –4
–
4
x
y
0
е) 1,5 y = 6, y = 4.
y
= 4
4
x
y
0
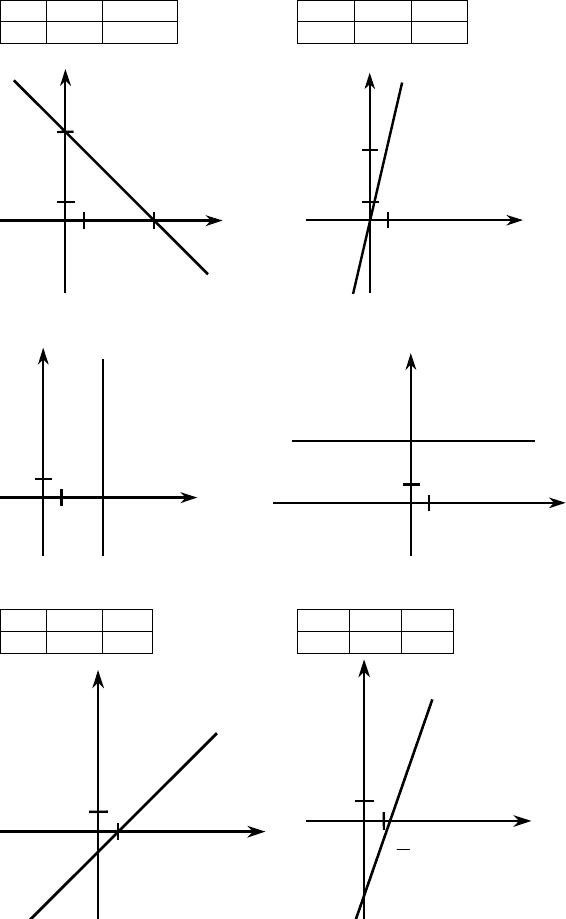
143
1113.
а) x + y = 5, y = 5 – x; б) y – 4x = 0; y = 4x;
x 0 5 x 0 1
y 5 0 y 0 4
1
1
5
x
y
0
5
4
1
1
x
y
0
в) 1,6x = 4,8; x = 3; г) 0,5y = 1,5; y = 3.
3
1
1
x
y
0
3
1
1
x
y
0
№1114.
а) x – y – 1 = 0; y = x – 1; б) 3x = y + 4; y = 3x – 4;
x 0 1 x 0 4/3
y –1 0 y –4 0
–
1
1
1
x
y
0
–
4
1
1
x
y
0
3
4
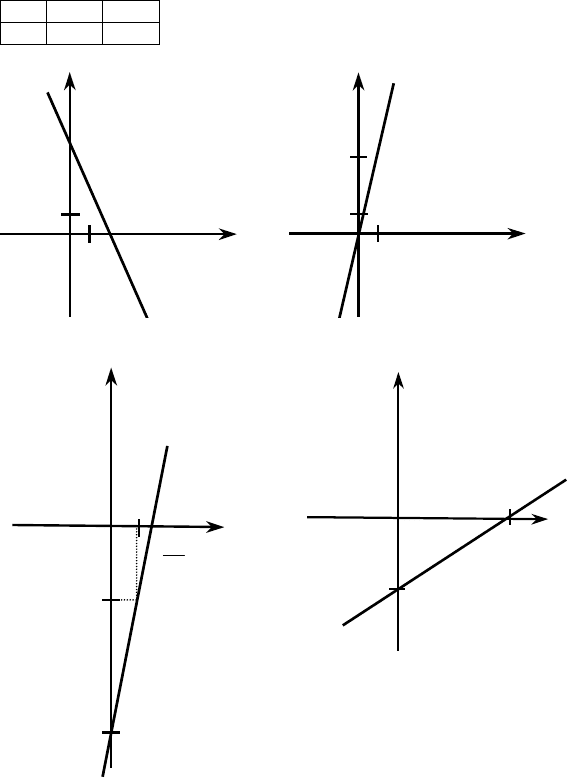
144
в) 2(x – y) + 3y = 4; г) (x + y) – (x – y) = 4;
2x – 2y + 3y = 4; y = 4 – 2x; 2y = 4; y = 2.
x 0 2
y 4 0
2
4
1
1
x
y
0
4
1
1
x
y
0
№1115. №1116.
–
20
21
16
4
–
7,4
3
x
y
0
11
–
8,8
x
y
0
Ответ: y = –8,8.
Ответ: y = –7,4.
№1117.
а) 12x – 8y = 25: y = 1,5x – 3 ⋅ 125.
Так как k = 1,5 > 0, то график проходит в I и III координатных четвертях.
Т.к. при x = 0 y = –3 ⋅ 125 < 0, то график проходит в IV четверти.
Ответ: I, III, IV.

145
б) 1,5y = 150: Так как график параллелен оси Оx и y > 0 для всех x, то гра-
фик проходит в I и II координатных четвертях.
Ответ: I, II.
в) 0,2x = 43: Так как график параллелен оси Оy и x > 0 для всех y, то график
проходит в I и IV координатных четвертях.
Ответ: I, IV.
№1118.
а)
16 18
0
812
xx−−
−=
, 3(16 – x) – 2(18 – x) = 0, 48–3x – 36 + 2x = 0, x = 12;
б)
15 2 1
10
28
xx−+
−+=
, 4(x – 15) – (2x + 1) + 8 = 0,
4x – 60 – 2x + 1 – 8 = 0, 2x = 67, x = 33,5.
№1119.
а) a(a – 4) – (a + 4)
2
= a
2
– 4a –a
2
– 8a – 16 = –12a – 16,
при a = –
4
1
1
: –12a – 16 = –12
1
1
4
⎛⎞
−
⎜⎟
⎝⎠
– 16 = 15 – 16 = –1;
б) (2a – 5)
2
–4(a – 1)(3 + a) = 4a
2
– 20a + 25 – 4(a
2
+ 3a – a– 3) =
= 4a
2
– 20a + 25 – 4a
2
–8a + 12 = –28a + 37,
при a =
1
12
: –28a + 37 = –28
1
12
+ 37 =
7337 104
33
−+⋅
= .
41. Системы линейных уравнений с двумя переменными
№1120.
а)
{
31 4
23 1 2–
+=
⋅=
{
44
52
=
≠
не решение; б)
{
224
22 2 2
+=
⋅
−=
{
44
22
=
=
решение.
№1121.
а)
{
33 ( 1) 8
73 2( 1) 23
–⋅+ =
⋅−⋅− =
{
88
23 23
=
=
решение; б)
{
1235
32(1)1
−+ ⋅ =
+
⋅− =
{
55
11
=
=
решение.
№1122.
а)
{
7
34 0
xy
:
xy
=−
+
=
{
347
3( 3) 44 0
−= −
⋅− + ⋅ =
{
33
70
−
=−
≠
(–3; 4) не решение
{
267
3 ( 2) 4 ( 6) 0
−=−−
⋅− + ⋅− =
{
213
30 0
−
≠−
−≠
(–2; –6) не решение
{
437
3( 4) 43 0
−=−
⋅− + ⋅ =
{
44
00
−=−
=
(–4; 3) решение
б)
{
30
54
xy
:
xy
−=
−
=−
{
3( 3) 4 0
5( 3) 4 4
⋅− − =
⋅− − =−
{
13 0
19 4
−≠
−
≠−
(–3; 4) не решение
{
3( 2) ( 6) 0
5( 2) ( 6) 4
⋅− −− =
⋅− −− =−
{
00
44
=
−=−
(–2; –6) решение
{
3( 4) 3 0
5( 4) 3 4
⋅− − =
⋅− − =−
{
15 0
23 4
−≠
−≠−
(–4; 3) не решение
146
№1123.
а)
{
40
5
xy
xy
−=
+=
б)
{
3
26
xy
xy
+=
−=−
№1124.
а)
{
1
1
1
39
3
3
yx
xy
xy
yx
=−
⎧
⎪
−=
⇒
⎨
+=
=−
⎪
⎩
y = x – 1
1
3
3
yx=−
x 0 1 x 0 9
y –1 0 y 3 0
2
3
1
–
1
x
y
0
3
9
Ответ: (3; 2).
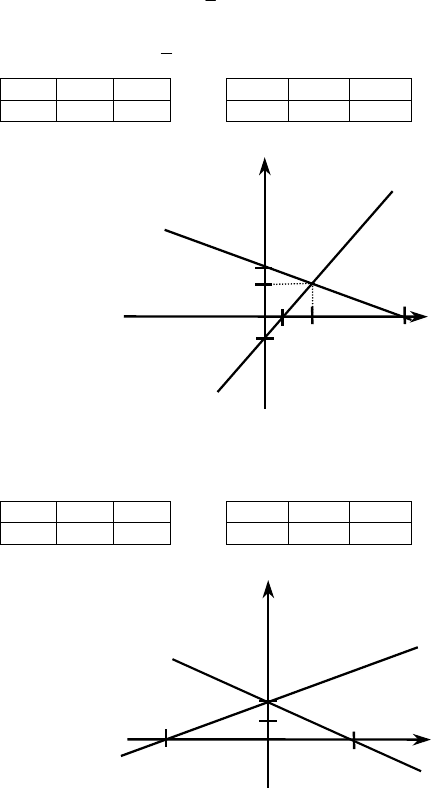
б)
{{
24 205
2510 204
x
yy,x
x
yy,x
+= =−
⇒
−+ = =+
у = 2 – 0,5х у = 2 + 0,4х
x 0 4 x 0 –5
y 2 0 y 2 0
2
4
–
5
x
y
0
1
Ответ: (2; 2)
147
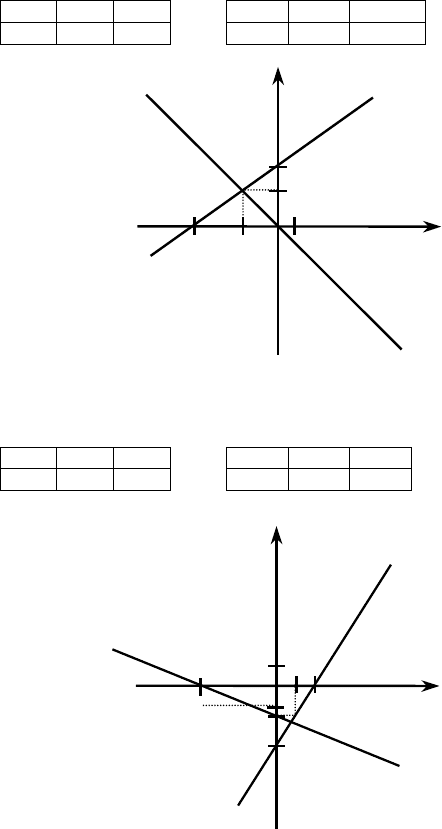
в)
{{
0
3414 07535
xy y x
x
yy,x,
+= =−
−+ = = +
у = –х у = 0,75х + 3,5
x 0 1 x 0 –14/3
y 0 –1 y 3,5 0
–
14/3
–
2
3
,
5
1
x
y
0
2
Ответ: (– 2; 2)
г)
{{
32 6 153
310 12 1203
xy y,x
x
yy,,x
−= = −
+=− =−−
у = 1,5х – 3 у = –1,2 – 0,3х
x 0 2 x 0 –4
y –3 0 y –1/2 0
–
1,2
–
41
2
x
y
0
1
–
3
–
1,5
Ответ: (1; –1,5)
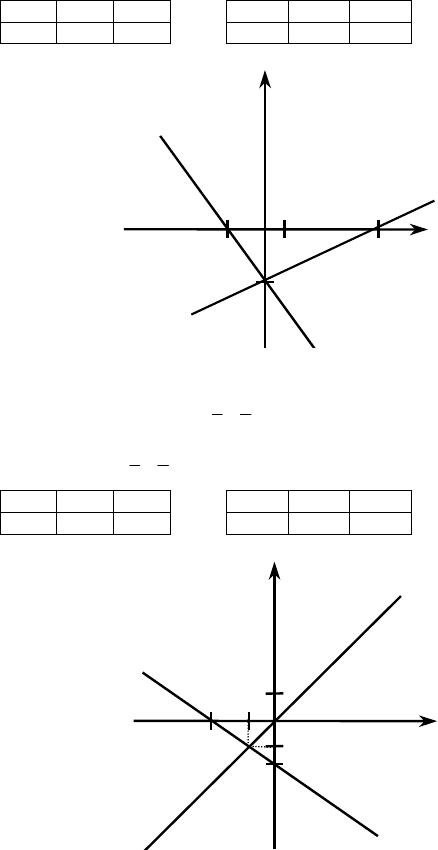
148
№1125.
а)
{{
26 053
32 6 315
xy y,x
x
yy,x
−= = −
+=− =−−
у = 0,5х – 3 у = –3 – 1,5х
x 0 6 x 0 –2
y –3 0 y –3 0
x
y
0
1
–
3
6
–
2
Ответ: (0; 3)
б)
{
0
52
23 5
33
yx
xy
xy
yx
=
⎧
⎪
−=
⎨
+=−
=− −
⎪
⎩
у = х
52
33
yx=− −
x 0 1 x 0 –2,5
y 0 1 y –5/3 0
1
–
2,5
x
y
0
–
1
–
5/3
–
1
Ответ: (–1; –1)

149
№1126.
а)
{
412
33
yx
yx
−=
+
=−
3025
1
3
y,
x
y
=+
⎧
⎪
⎨
=− −
⎪
⎩
Т.к. 0,25 ≠ –
1
3
, то графики пересекаются, а, значит, решение одно.
б)
{
30
36
yx
yx
−=
−
=
3
1
2
3
yx
yx
=
⎧
⎪
⎨
=+
⎪
⎩
Т.к. 3 ≠
1
3
, то графики пересекаются, а, значит, решение одно.
в)
{
15 1
32 2
,x
xy
=
−+ =−
2
3
215
x
y,x
⎧
⎪
=
⎨
⎪
=− +
⎩
Графики этих функций пересекаются, а, значит, решение одно.
г)
{
23
05
xy
y,x
+=
=−
{
15 05
05
y, ,x
y,x
=−
=−
Т.к. –0,5 ≠ –0,5; 1,5 ≠ 0, то графики пересекаются, а, значит, решений нет.
д)
{
2113
6224
x
y
yx
=−
=−
{
2113
2113
x
y
x
y
=−
=−
Т.к. два эти уравнения совпадают, то решений бесконечно много.
е)
{
28
410
xy
xy
−+ =
+=
{
405
25 025
y,x
y, ,x
=+
=−
Т.к. 0,5≠–0,25, то графики этих функций пересекаются, а, значит, решение одно.
№1127.
а)
{
61
210 3
xy
xy
=−
−
=
{
61
515
xy
x
y,
=−
=+
Т.к. 6 ≠ 5, то графики этих функций пересекаются, а, значит, решение одно.
б)
{
54
60
xy
xy
+=
+−=
{
45
6
yx
yx
=−
=−
Т.к. –5≠–1, то графики этих функций пересекаются, а, значит, решение одно.
в)
{
12 3 5
624 10
xy
yx
−=
−
=−
{
24 6 10
62410
xy
yx
−=
−+ =
Т.к. два эти уравнения совпадают, то решений бесконечно много.
№1128.
а)
{
35
3915
xy
xy
−=
−
=
, x – 3y = 5; (5; 0); (11; 2); (8; 1) — решения системы.
б)
{
15 05
23 1
,y x ,
xy
+=−
+=−
, 2x + 3y = –1;
1
0
3
;
⎛⎞
−
⎜⎟
⎝⎠
; (1; –1);
1
0
2
;
⎛⎞
−
⎜⎟
⎝⎠
— решения системы.

150
№1129.
а)
23 1
3
42
xx
x
−+
−=
, 2x – 3 – 12x = 2(x + 1), 2x – 12x – 2x = 2 + 3,
12x = –5, x = –
5
12
;
б)
31
6
35
x
x−
=−
, 6 ⋅ 15 = 5(3x – 1) – 3x, 90 = 15x – 5 – 3x,
12x = 95, x =
95 11
7
12 12
=
.
№1130.
а) (5c
2
– c + 8)(2x – 3) – 16 = 10c
3
– 15c
2
– 2c
2
+ 6c + 16c – 24 – 16 =
= 10c
3
– 17c
2
+ 24c – 40;
б) 18m
3
–(3m–4)(6m
2
+m–2)=18m
3
–(18m
3
+ 3m
2
– 6m – 24m
2
– 4m + 8) =
= –3m
2
+ 6m + 24m
2
+ 4m – 8 = 21m
2
+ 10m – 8.
№1131.
а) a
3
+a
2
–x
2
a–x
2
=a
2
(a + 1) – x
2
(a + 1) = (a
2
– x
2
)(a+1)=(a–x)(a+x)(a + 1);
б) b
3
+b
2
c – 9b–9c=b
2
(b + c)–9(b + c)=(b
2
– 9)(b+c)=(b – 3)(b+3)(b + c).
§ 16. Решение систем линейных уравнений
42. Способ подстановки
№1132.
а)
{
1
5216
yx
xy
=−
+
=
, 5x + 2(x – 1) = 16, 5x + 2x – 2 = 16,
7x = 18, x =
18 4
2
77
= , y =
44
211
77
−= .
Ответ:
44
21
77
;
⎛⎞
⎜⎟
⎝⎠
.
б)
{
2
32110
xy
xy
=−
−
−=
, 3(2 – y) – 2y – 11 = 0, 5y = –5, y = –1, x = 2 – (–1) = 3.
Ответ: (3; –1).
№1133.
а)
{
21
67
yx
xy
−=
−
=
, y = 2x + 1, 6x – (2x + 1) = 7,
6x – 2x – 1 = 7, 4x = 8, x = 2, тогда y = 2 ⋅ 2 + 1 = 5.
Ответ: (2; 5).
б)
{
7313
25
xy
xy
−
=
−=
, x = 2y + 5, 7(2y + 5) – 3y = 13,
14y + 35 – 3y = 13, 11y = –22, y = –2, значит, x = 2 ⋅ (–2) + 5 = 1;
Ответ: (1; –2).
