Morling K. Geometric and Engineering Drawing
Подождите немного. Документ загружается.

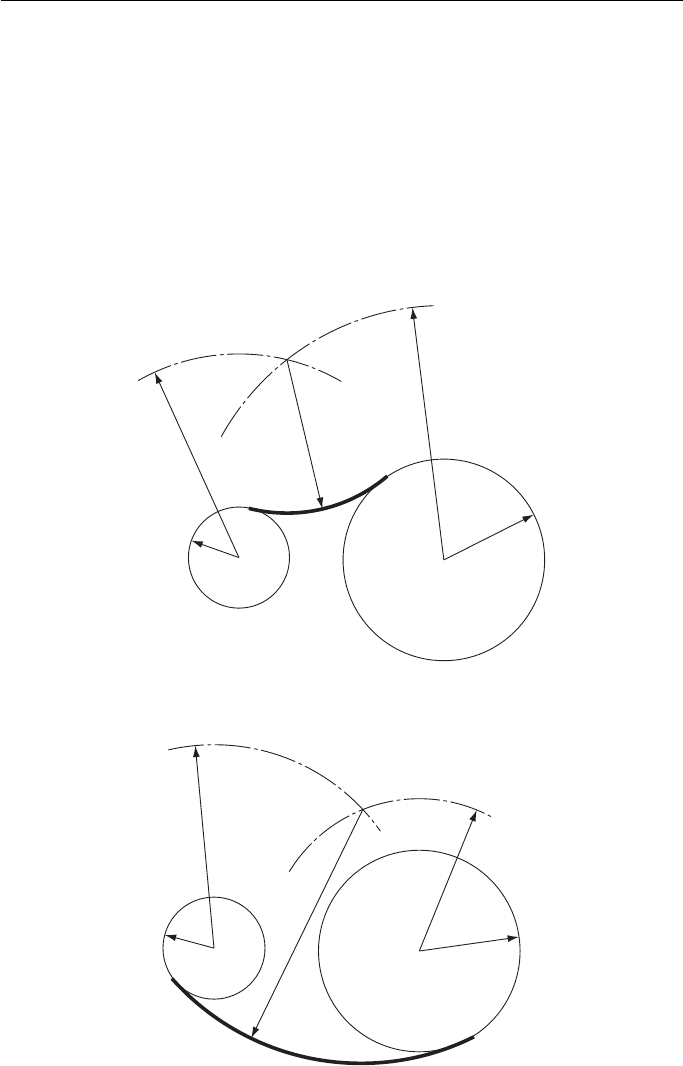
Geometric and Engineering Drawing94
To find the centre of an arc, radius R , which blends with two circles, centres
A and B, radii r
1
and r
2
, respectively.
There are two possible centres, shown in Figs. 8.6 and 8.7 .
If an arc, radius R , is to blend with a circle, radius r , the centre of the arc must
be distance R from the circumference and hence R r ( Fig. 8.6 ) or R r ( Fig. 8.7 )
from the centre of the circle.
With centre A, radius R r
1
, draw an arc.
With centre B, radius R r
2
, draw an arc to intersect the first arc in O.
O is the required centre.
B
O
A
R + r
2
R + r
1
R
r
2
r
1
Figure 8.6
O
A
R – r
1
R – r
2
B
r
1
r
2
R
Figure 8.7
The Blending of Lines and Curves 95
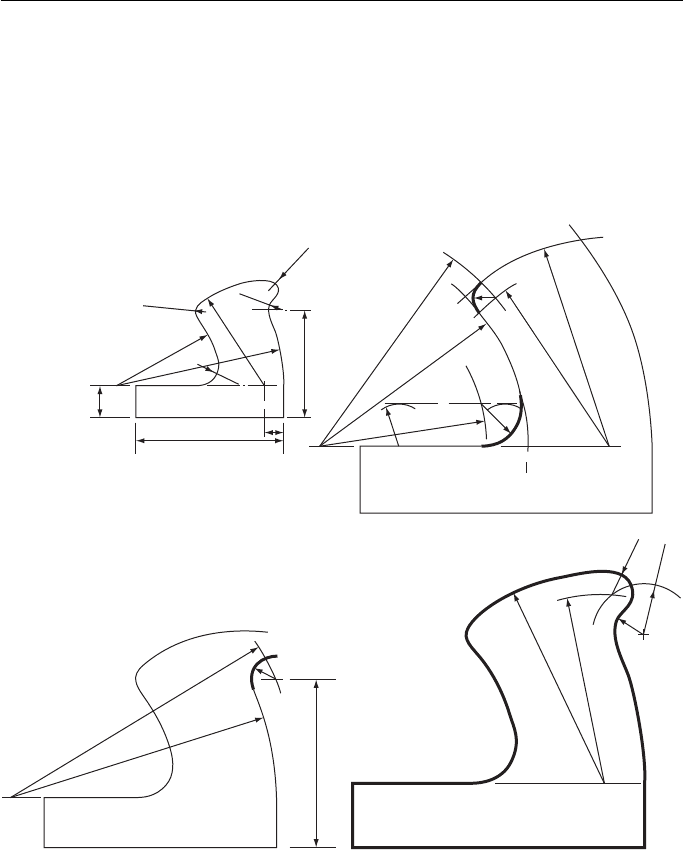
The alternative construction is:
With centre A, radius R – r
1
, draw an arc.
With centre B, radius R – r
2
, draw an arc to intersect the first arc in O.
O is the required centre.
These seven constructions will enable you to blend radii in all the conditions that
you are likely to meet (Figure 8.8) .
5 R
7 R
5 R
70
50
5
7
7 + 5
7
50
50 – 5
10
10
50 – 10
10 R
Dimensions in mm
scale 1:2
10
80 + 7
80
50
50 + 5
50
50 R
80 R
50 R
15
5
Stage 1
Stage 2 Stage 3
50
50 – 5
Figure 8.8 The outline of a plane handle drawn in three stages to show how the radii are
blended.
The construction lines have been left off each successive stage for clarity but if
you are answering a similar question during an examination, leave all the construc-
tion lines showing. If you do not, the examiner may assume that you found the cen-
tres by trial and error and you will lose the majority of the marks.
There are three more constructions that are included in the blending of lines and
curves and these are shown below.
Geometric and Engineering Drawing96
To join two parallel lines with two equal radii, the sum of which equals the
distance between the lines ( Fig. 8.9 ).
Draw the centre line between the parallel lines.
From a point A, drop a perpendicular to meet the centre line in O
1
.
With centre O
1
, radius O
1
A, draw an arc to meet the centre line in B.
Produce AB to meet the other parallel line in C.
From C erect a perpendicular to meet the centre line in O
2
.
With centre O
2
, radius O
2
C, draw the arc BC.
O
2
O
1
B
C
A
Figure 8.9
A
C
B
r
r
O
1
O
2
Figure 8.10
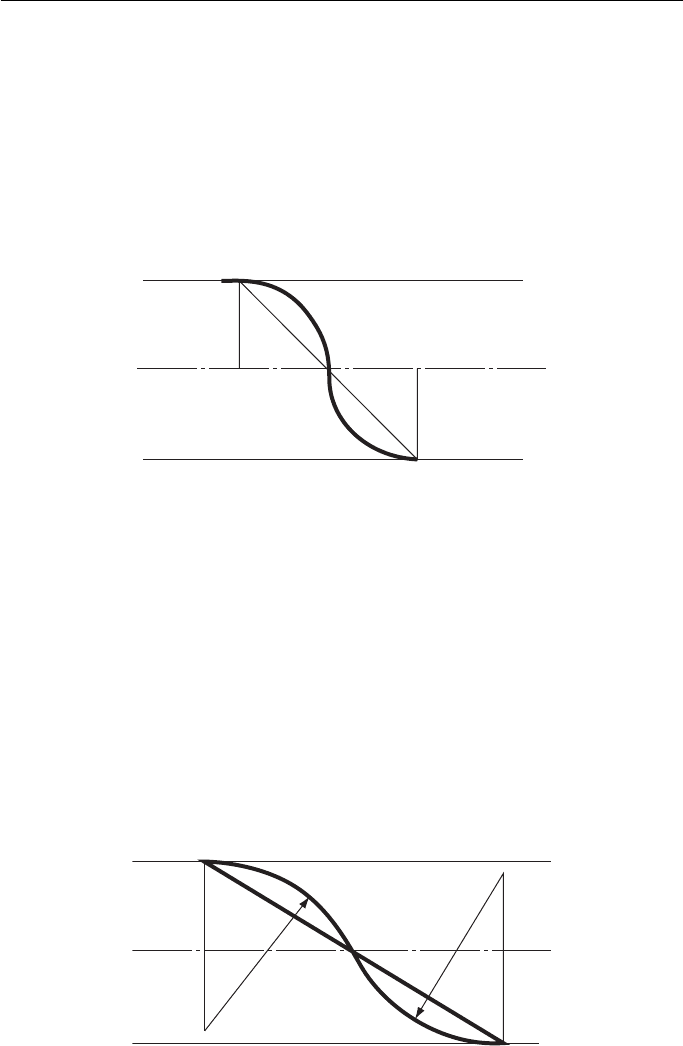
To join two parallel lines with two equal radii, r , the sum of which is greater
than the distance between the lines ( Fig. 8.10 ).
Draw the centre line between the parallel lines.
From a point A, drop a perpendicular and on it mark off AO
1
r .
Draw the centre line between the parallel lines.
From a point A, drop a perpendicular and on it mark off AO
1
r.
With centre O
1
, radius r , draw an arc to meet the centre line in B.
Produce AB to meet the other parallel line in C.
From C erect a perpendicular CO
2
r.
With centre O
2
, radius r , draw the arc BC.
The Blending of Lines and Curves 97
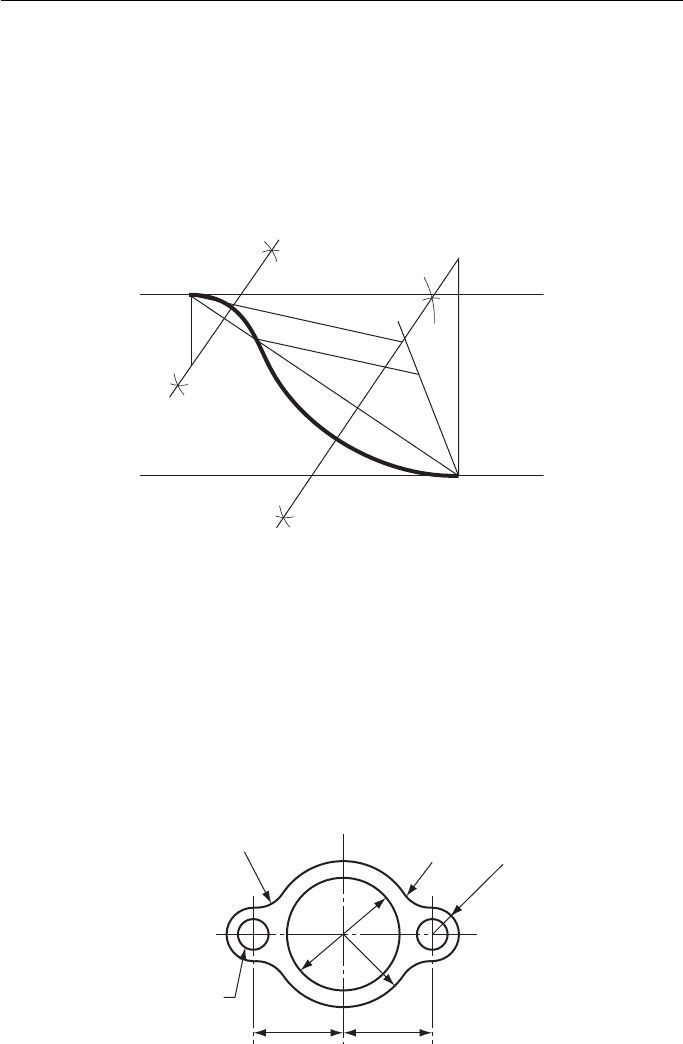
To join two parallel lines with two unequal radii (e.g. in the ratio of 3:1) given
the ends of the curve A and B ( Fig. 8.11 ).
Join AB and divide into the required ratio, AC:CB 1:3.
Perpendicularly bisect AC to meet the perpendicular from A in O
1
.
With centre O
1
, radius O
1
A, draw the arc AC.
Perpendicularly bisect CB to meet the perpendicular from B in O
2
.
With centre O
2
and radius O
2
B, draw the arc CB.
O
2
O
1
C
A
B
Figure 8.11
72
2-
φ25
holes
Dimensions in mm
72
R58
R33
R33
R21
φ88
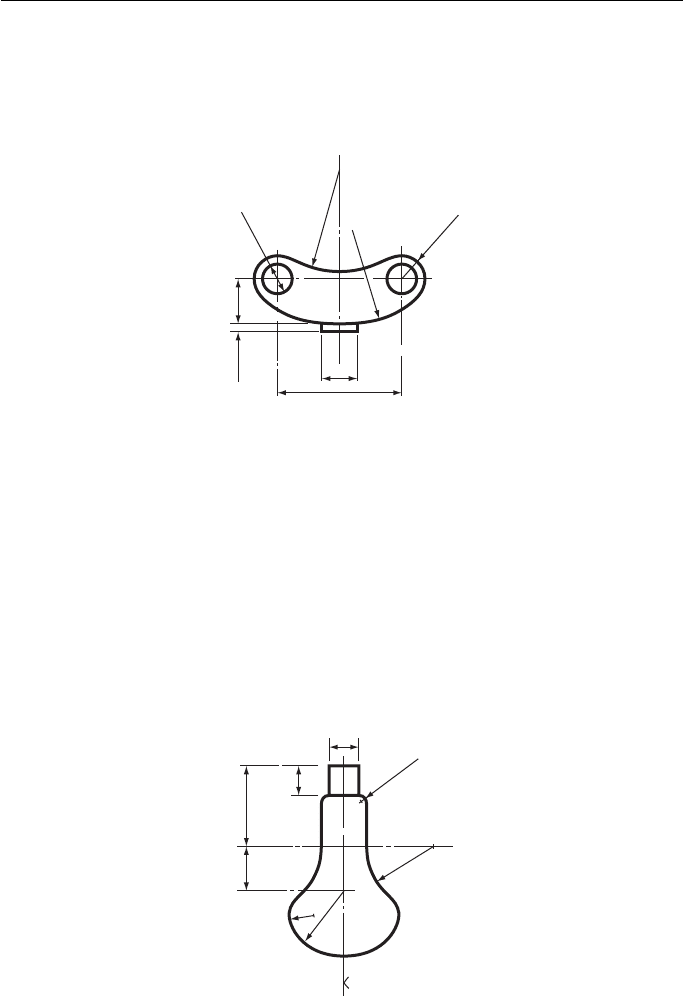
Figure 1
Exercise 8
(All questions originally set in imperial units.)
1. Figure 1 shows an exhaust pipe gasket. Draw the given view full size and show any con-
structions used in making your drawing. Do not dimension your drawing.
Southern Regional Examinations Board
Geometric and Engineering Drawing98
24
R6
R48
R48
R18
21
6033
Dimensions in mm
AB
Figure 3
Dimensions in mm
50
12
R9
R38
R40
φ 12
318
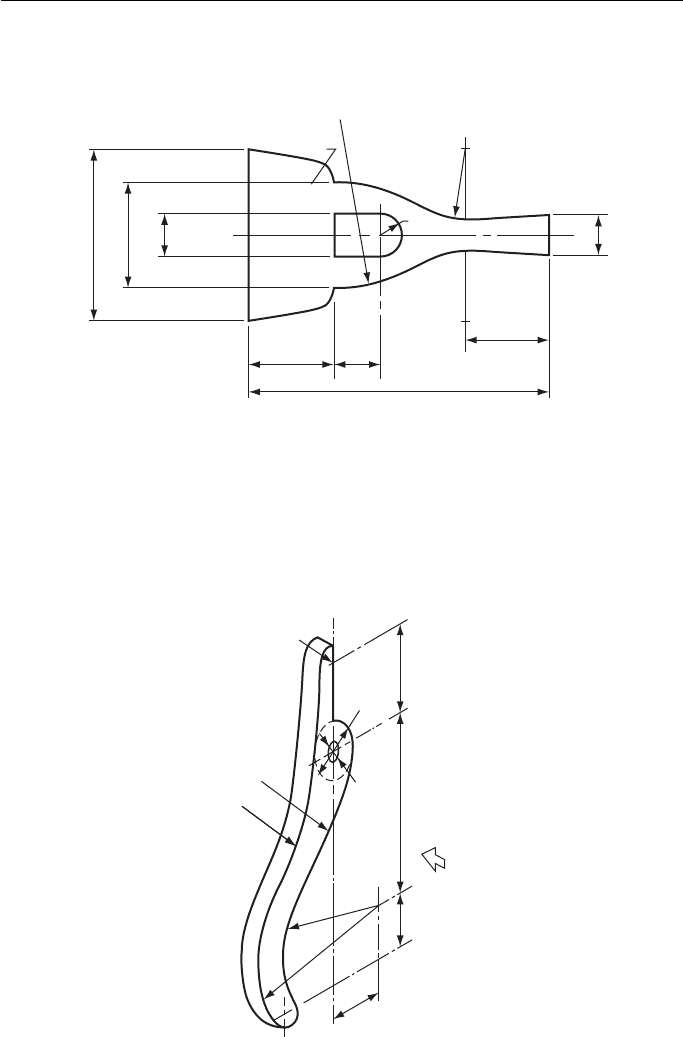
Figure 2
3. Figure 3 shows the outline of an electric lamp.
Important – Construction lines must be visible, showing clearly how you obtained the cen-
tres of the arcs and the exact positions of the junctions between arcs and straight lines.
Part 1. Draw the shape, full size .
Part 2 . Line AB is to be increased to 28 mm. Construct a scale and using this scale draw
the left half or right half of the shape, increasing all other dimensions proportionally.
Southern Regional Examinations Board
2. Figure 2 is an elevation of the turning handle of a can opener. Draw this view, twice full
size, showing clearly the method of establishing the centres of the arcs.
East Anglian Examinations Board
The Blending of Lines and Curves 99
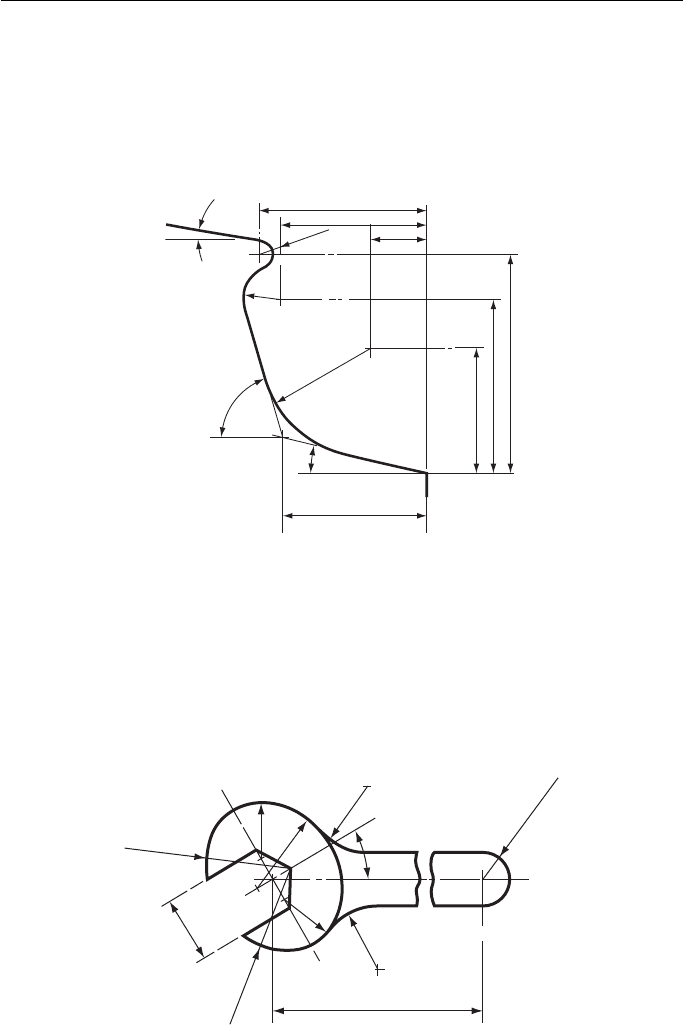
5. Figure 5 shows one half of a pair of pliers. Draw, full size, a front elevation looking from A.
Your constructions for finding the centres of the arcs must be shown.
South-East Regional Examinations Board
Dimensions in mm
178
50
25
29
R12
R12
R82
R50
50
24
62
100
Figure 4
Dimensions in mm
R9
36
R60
R60
R72
φ 24
φ 12
R42
81
33
33
A
Figure 5
4. Figure 4 shows a garden hoe. Draw this given view, full size, and show any construction
lines used in making the drawing. Do not dimension the drawing.
Southern Regional Examinations Board
Geometric and Engineering Drawing100
6. Figure 6 shows the design for the profile of a sea wall. Draw the profile of the sea wall to a
scale of 10 mm 2 m. Measure in metres the dimensions A, B, C and D and insert these on
your drawing. In order to do this you should construct an open divided scale of 10 mm 2 m
to show units of 1 m .
Constructions for obtaining the centres of the radii must be clearly shown.
Metropolitan Regional Examinations Board
200
Dimensions in mm
40
30°
R38
R15
R38
R38
R50
R50
R50
R32
Figure 7
7. Details of a spanner for a hexagonal nut are shown in Fig. 7 . Draw this outline showing
clearly all constructions. Scale: full size.
Oxford Local Examinations
Dimensions in mm
7
C
8
A
B
D
10
15°
74°
8°
R5
R2
R1
Figure 6
The Blending of Lines and Curves 101
Dimensions in mm
140
68
R 150
R 150
R24
R20
R60
R88
R38
R88
R38
26 26
50 5044
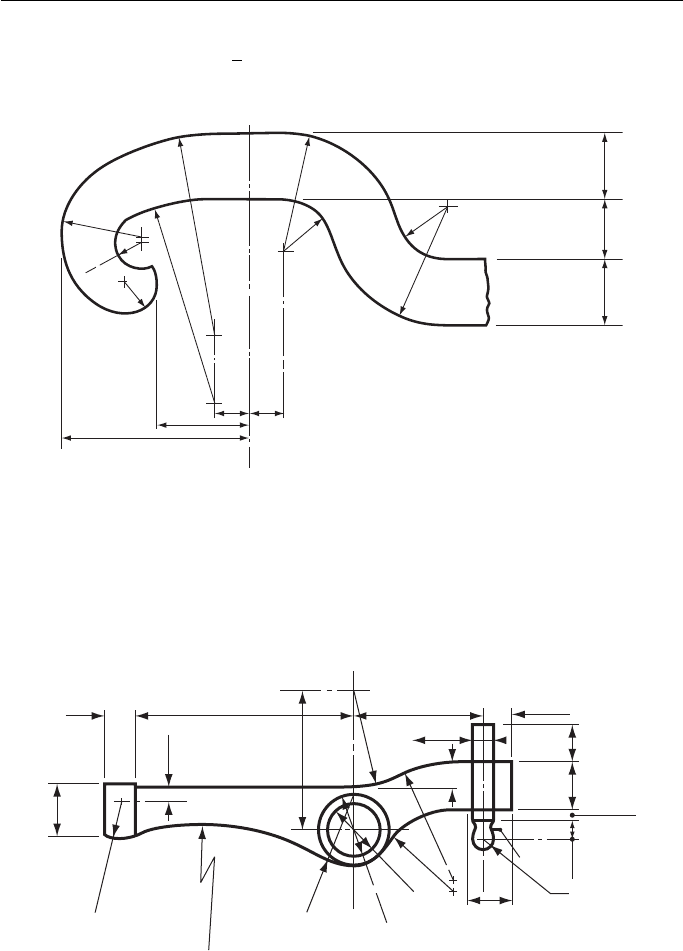
Figure 8
Dimensions in mm
R57
R19
R 21.5
R32
φ 18
φ 14
R25
R 9.5
12.5
7.5
6.5
9.5
3
5
10
12.5
65
57 35
3
38
R3
φ 6.5
Figure 9
8. The end of the lever for a safety valve is shown in Fig. 8 . Draw this view, showing clearly
all construction lines. Scale:
1
2
full size.
Oxford Local Examinations
9. Draw, to a scale of 2:1, the front elevation of a rocker arm as illustrated in Fig. 9 .
Oxford Local Examinations
This page intentionally left blank
Geometric and Engineering Drawing. DOI:
© 2010 Elsevier Ltd. All rights reserved.2010
10.1016/B978-0-08-096768-4.00009-7
Loci
Definition
A locus (plural loci ) is the path traced out by a point that moves under given definite
conditions.
You may not have been aware of it, but you have met loci many times before.
One of the most common loci is that of a point that moves so that its distance from
another fixed point remains constant: this produces a circle. Another locus that you
know is that of a point that moves so that its distance from a line remains constant:
this produces parallel lines.
Problems on loci can take several different forms. One important practical appli-
cation is finding the path traced out by points on mechanisms. This may be done
simply to see if there is sufficient clearance around a mechanism or, with further
knowledge beyond the scope of this book, to determine the velocity and hence the
forces acting upon a component.
There are very few rules to learn about loci; it is mainly a subject for common
sense. A locus is formed by continuous movement and you have to ‘ stop ’ the move-
ment several times and find and plot the position of the point that you are interested
in. Take, for instance, the case of the man who was too lazy to put wedges under his
ladder. The inevitable happened and the ladder slipped. The path that the feet of the
man took is shown in Fig. 9.1 .
The top of the ladder slips from T to T
9
. The motion of the top of the ladder has
been stopped at T
1
, T
2
, T
3
, etc., and, since the length of the ladder remains constant,
the corresponding positions of the bottom of the ladder, B
1
, B
2
, B
3
, etc., can be
found. The positions of the ladder, T
1
B
1
, T
2
B
2
, T
3
B
3
, etc., are drawn and the posi-
tion of the man ’ s feet, 1, 2, 3, etc., are marked. The points are joined together with
a smooth curve. It is interesting to note that the man hits the ground at right angles
(assuming that he remains on the ladder). The resulting jar often causes serious
injury and is one of the reasons for using chocks.
Another simple example is the locus of the end of a bureau door stay ( Fig. 9.2 ).
This type of stay is also often used on wardrobe doors. Its function is to allow the
door to open to a certain point, and then to support the door in that position.
The stay, of course, has two ends and the locus on one end is easily found: it is an
arc whose centre is the hinge. The other end of the stay is allowed to slide through
the pin but it is not allowed to move off it. As the end of the stay moves along the arc,
its movement is stopped several times and the position of the other end of the stay is
marked. These points are joined together with a smooth curve. Obviously the designer
of such a bureau would have to plot this locus before deciding the depth of the bureau.
9
