Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics
Подождите немного. Документ загружается.


where z is the amount of CO, in kmol, present in the exiting mixture for each kmol of CO
entering the reactor.
Accordingly, there are two unknowns: z and the temperature of the exiting stream. To
solve a problem with two unknowns requires two equations. One is provided by an energy
equation. If the exiting gas mixture is in equilibrium, the other equation is provided by the
equilibrium constant, Eq. 14.35. The temperature of the products may then be called the
equilibrium flame temperature. The equilibrium constant used to evaluate the equilibrium
flame temperature would be determined with respect to
Although only the dissociation of CO
2
has been discussed, other products of combustion
may dissociate, for example
When there are many dissociation reactions, the study of chemical equilibrium is facilitated
by the use of computers to solve the simultaneous equations that result. Simultaneous reac-
tions are considered in Sec. 14.4.4. The following example illustrates how the equilibrium
flame temperature is determined when one dissociation reaction occurs.
N
2
S
d
2N
N
2
S
d
2H
O
2
S
d
2O
H
2
O
S
d
OH
1
2
H
2
H
2
O
S
d
H
2
1
2
O
2
CO
2
S
d
CO
1
2
O
2
.
696 Chapter 14 Chemical and Phase Equilibrium
equilibrium flame
temperature
EXAMPLE 14.6 Determining the Equilibrium Flame Temperature
Carbon monoxide at 25C, 1 atm enters a well-insulated reactor and reacts with the theoretical amount of air entering at the
same temperature and pressure. An equilibrium mixture of CO
2
, CO, O
2
, and N
2
exits the reactor at a pressure of 1 atm. For
steady-state operation and negligible effects of kinetic and potential energy, determine the composition and temperature of the
exiting mixture in K.
SOLUTION
Known: Carbon monoxide at 25C, 1 atm reacts with the theoretical amount of air at 25C, 1 atm to form an equilibrium
mixture of CO
2
, CO, O
2
, and N
2
at temperature T and a pressure of 1 atm.
Find: Determine the composition and temperature of the exiting mixture.
Schematic and Given Data:
Air
25°C, 1 atm
Insulation
(CO
2
, CO, O
2
, N
2
)
T, 1 atm
CO
25°C, 1 atm
Figure E14.6
Assumptions:
1. The control volume shown on the accompany-
ing sketch by a dashed line operates at steady state
with and negligible effects of
kinetic and potential energy.
2. The entering gases are modeled as ideal gases.
3. The exiting mixture is an ideal gas mixture at
equilibrium.
Q
#
cv
0, W
#
cv
0,

14.4 Further Examples of the Use of the Equilibrium Constant 697
Analysis: The overall reaction is the same as in the solution to Example 14.4
By assumption 3, the exiting mixture is an equilibrium mixture. The equilibrium constant expression developed in the solu-
tion to Example 14.4 is
(a)
Since p 1 atm, Eq. (a) reduces to
(b)
This equation involves two unknowns: z and the temperature T of the exiting equilibrium mixture.
Another equation involving the two unknowns is obtained from the energy rate balance, Eq. 13.12b, which reduces with
assumption 1 to
(c)
where
and
The enthalpy of formation terms set to zero are those for oxygen and nitrogen. Since the reactants enter at 25C, the corre-
sponding terms also vanish. Collecting and rearranging, we get
(d)
Equations (b) and (d) are simultaneous equations involving the unknowns z and T. When solved iteratively using tabular data,
the results are z 0.125 and T 2399 K, as can be verified. The composition of the equilibrium mixture, in kmol per kmol
of CO entering the reactor, is then 0.125CO, 0.0625O
2
, 0.875CO
2
, 1.88N
2
.
z 1¢h
2
CO
z
2
1¢h2
O
2
11 z2 1¢h2
CO
2
1.881¢h2
N
2
11 z231h°
f
2
CO
2
1h°
f
2
CO
4 0
¢h
h
P
z1h°
f
¢h2
CO
z
2
1h°
f
0
¢h2
O
2
11 z2 1h°
f
¢h2
CO
2
1.881h°
f
0
¢h2
N
2
h
R
1h°
f
¢h
0
2
CO
1
2
1h°
f
0
¢h
0
2
O
2
1.881h°
f
0
¢h
0
2
N
2
h
R
h
P
K1T 2
z
11 z2
a
z
5.76 z
b
1
2
K1T 2
z1z
22
1
2
11 z2
a
p
p
ref
15.76 z2
2
b
1
2
CO
1
2
O
2
1.88N
2
S z CO
z
2
O
2
11 z2 CO
2
1.88N
2
As illustrated by Example 14.7, the equation solver and property retrieval features of
Interactive Thermodynamics: IT allow the equilibrium flame temperature and composition
to be determined without the iteration required when using table data.
EXAMPLE 14.7 Determining the Equilibrium Flame Temperature Using Software
Solve Example 14.6 using Interactive Thermodynamics: IT and plot equilibrium flame temperature and z, the amount of CO
present in the exiting mixture, each versus pressure ranging from 1 to 10 atm.
SOLUTION
Known: See Example 14.6.

698 Chapter 14 Chemical and Phase Equilibrium
Find: Using IT, plot the equilibrium flame temperature and the amount of CO present in the exiting mixture of Example 14.6,
each versus pressure ranging from 1 to 10 atm.
Assumptions: See Example 14.6.
Analysis: Equation (a) of Example 14.6 provides the point of departure for the IT solution
(a)
For a given pressure, this expression involves two unknowns: z and T.
Also, from Example 14.6, we use the energy balance, Eq. (c)
(c)
where
and
where the subscripts R and P denote reactants and products, respectively, and z denotes the amount of CO in the products, in
kmol per kmol of CO entering.
With pressure known, Eqs. (a) and (c) can be solved for T and z using the following IT code. Choosing SI from the Units
menu and amount of substance in moles, and letting hCO_R denote the specific enthalpy of CO in the reactants, and so on,
we have
// Given data
TR = 25 + 273.15 // K
p = 1 // atm
pref = 1 // atm
// Evaluating the equilibrium constant using Eq. (a)
K = ((z * (z/2)
^
0.5) / (1 – z)) * ((p / pref) / ((5.76 + z) / 2))
^
0.5
// Energy balance: Eq. (c)
hR = hP
hR = hCO_R + (1/2) * hO2_R + 1.88 * hN2_R
hP = z * hCO_P + (z / 2) * hO2_P + (1 – z) * hCO2_P + 1.88 * hN2_P
hCO_R = h_T(“CO”,TR)
hO2_R = h_T(“O2”,TR)
hN2_R = h_T(“N2”,TR)
hCO_P = h_T(“CO”,T)
hO2_P = h_T(“O2”,T)
hCO2_P = h_T(“CO2”,T)
hN2_P = h_T(“N2”,T)
/* To obtain data for the equilibrium constant use the Lookup Table
option under the Edit menu. Load the file “eqco2.lut”. Data for
CO2 CO + 1/2 O2 from Table A-27 are stored in the look-up table
as T in column 1 and log10(K) in column 2. To retrieve the data use
*/
log(K) = lookupval(eqco2,1,T,2)
Obtain a solution for p 1 using the Solve button. To ensure rapid convergence, restrict T and K to positive values, and set
a lower limit of 0.001 and an upper limit of 0.999 for z. The results are T 2399 K and z 0.1249, which agree with the
values obtained in Example 14.6.
S
d
h
P
z1h
CO
2
P
1z
22 1h
O
2
2
P
11 z2 1h
CO
2
2
P
1.881h
N
2
2
P
h
R
1h
CO
2
R
1
2
1h
O
2
2
R
1.881h
N
2
2
R
h
R
h
P
K1T 2
z1z
22
1
2
11 z2
c
p
p
ref
15.76 z2
2
d
1
2
❶
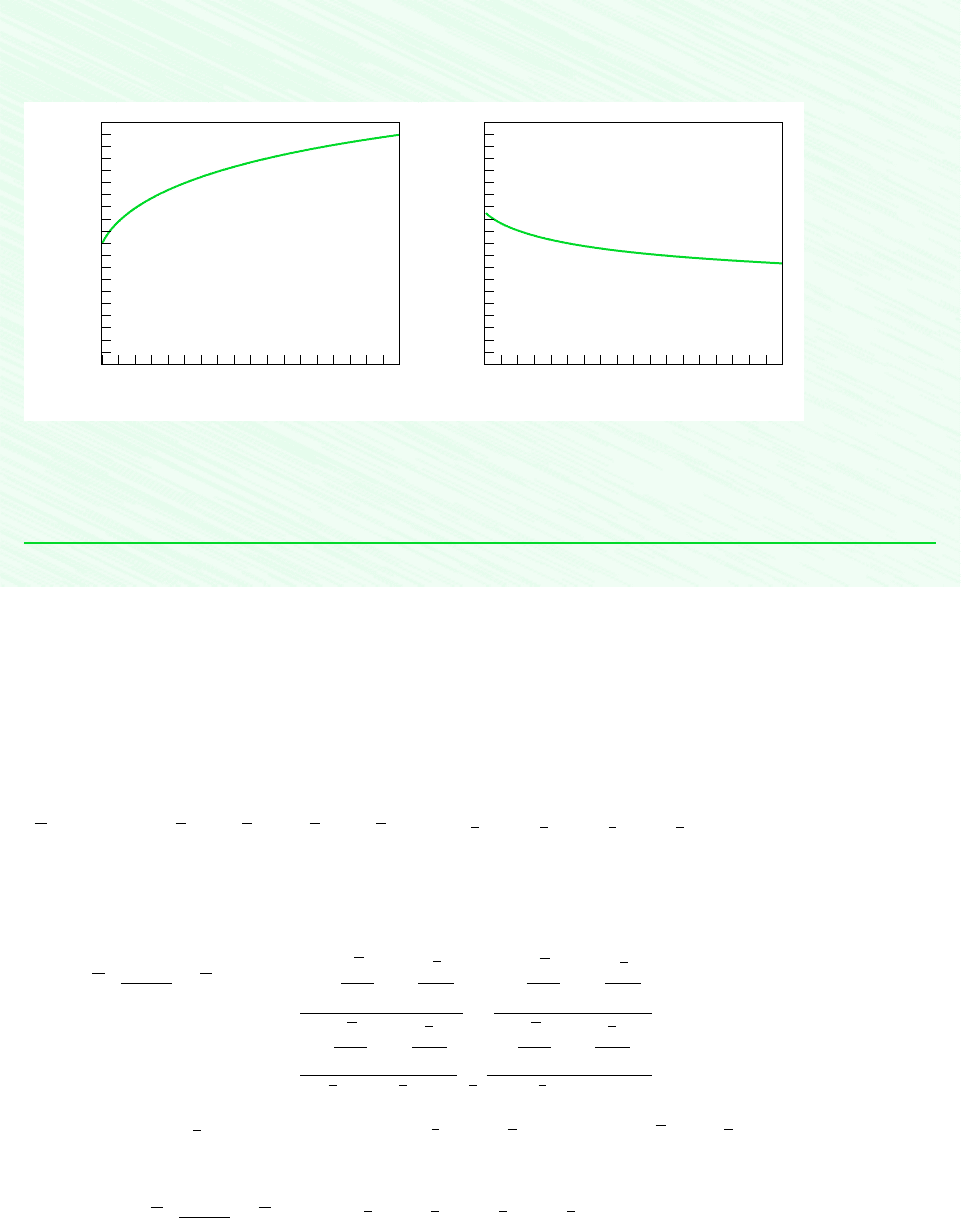
14.4 Further Examples of the Use of the Equilibrium Constant 699
Now, use the Explore button and sweep p from 1 to 10 atm in steps of 0.01. Using the Graph button, construct the
following plots:
T (K)
2500
2450
2400
2350
2300
24681013579
p (atm)
z
0.2
0.15
0.1
0.05
0
24681013579
p (atm)
Figure E14.7
From Fig. E14.7, we see that as pressure increases more CO is oxidized to CO
2
(z decreases) and temperature increases.
Similar files are included in IT for each of the reactions in Table A-27.
❶
14.4.2 Van’t Hoff Equation
The dependence of the equilibrium constant on temperature exhibited by the values of
Table A-27 follows from Eq. 14.31. An alternative way to express this dependence is given
by the van’t Hoff equation, Eq. 14.43b.
The development of this equation begins by introducing Eq. 14.29b into Eq. 14.31 to
obtain on rearrangement
(14.41)
Each of the specific enthalpies and entropies in this equation depends on temperature alone.
Differentiating with respect to temperature
From the definition of (T ) (Eq. 6.20), we have Moreover,
Accordingly, each of the underlined terms in the above equation vanishes identically, leaving
(14.42)RT
d ln K
dT
R ln K 1n
C
s °
C
n
D
s °
D
n
A
s °
A
n
B
s °
B
2
dh
dT c
p
.d s °
dT c
p
T.s °
1n
C
s °
C
n
D
s °
D
n
A
s °
A
n
B
s °
B
2
n
A
a
d h
A
dT
T
d s °
A
dT
b n
B
a
d h
B
dT
T
d s °
B
dT
bd
RT
d ln K
dT
R ln K cn
C
a
d
h
C
dT
T
d
s °
C
dT
b n
D
a
d h
D
dT
T
d s °
D
dT
b
RT ln K 31n
C
h
C
n
D
h
D
n
A
h
A
n
B
h
B
2 T 1n
C
s °
C
n
D
s °
D
n
A
s °
A
n
B
s °
B
24
Using Eq. 14.41 to evaluate the second term on the left and simplifying the resulting ex-
pression, Eq. 14.42 becomes
(14.43a)
or, expressed more concisely
(14.43b)
which is the van’t Hoff equation.
In Eq. 14.43b, H is the enthalpy of reaction at temperature T. The van’t Hoff equation
shows that when H is negative (exothermic reaction), K decreases with temperature, whereas
for H positive (endothermic reaction), K increases with temperature.
The enthalpy of reaction H is often very nearly constant over a rather wide interval of
temperature. In such cases, Eq. 14.43b can be integrated to yield
(14.44)
where K
1
and K
2
denote the equilibrium constants at temperatures T
1
and T
2
, respectively.
This equation shows that ln K is linear in 1T. Accordingly, plots of ln K versus 1T can be
used to determine H from experimental equilibrium composition data. Alternatively, the
equilibrium constant can be determined using enthalpy data.
14.4.3 Ionization
The methods developed for determining the equilibrium composition of a reactive ideal gas
mixture can be applied to systems involving ionized gases, also known as plasmas. In pre-
vious sections we considered the chemical equilibrium of systems where dissociation is a
factor. For example, the dissociation reaction of diatomic nitrogen
can occur at elevated temperatures. At still higher temperatures, ionization may take place
according to
(14.45)
That is, a nitrogen atom loses an electron, yielding a singly ionized nitrogen atom N
and a
free electron e
. Further heating can result in the loss of additional electrons until all elec-
trons have been removed from the atom.
For some cases of practical interest, it is reasonable to think of the neutral atoms,
positive ions, and electrons as forming an ideal gas mixture. With this idealization, ion-
ization equilibrium can be treated in the same manner as the chemical equilibrium of re-
acting ideal gas mixtures. The change in the Gibbs function for the equilibrium ioniza-
tion reaction required to evaluate the ionization-equilibrium constant can be calculated as
a function of temperature by using the procedures of statistical thermodynamics. In
general, the extent of ionization increases as the temperature is raised and the pressure is
lowered.
Example 14.8 illustrates the analysis of ionization equilibrium.
N
S
d
N
e
N
2
S
d
2N
ln
K
2
K
1
¢H
R
a
1
T
2
1
T
1
b
d ln K
dT
¢H
RT
2
d ln K
dT
1n
C
h
C
n
D
h
D
n
A
h
A
n
B
h
B
2
RT
2
700 Chapter 14 Chemical and Phase Equilibrium
van’t Hoff equation

14.4 Further Examples of the Use of the Equilibrium Constant 701
EXAMPLE 14.8 Considering Ionization Equilibrium
Consider an equilibrium mixture at 2000K consisting of Cs, Cs
, and e
, where Cs denotes neutral cesium atoms, Cs
singly
ionized cesium ions, and e
free electrons. The ionization-equilibrium constant at this temperature for
is K 15.63. Determine the pressure, in atmospheres, if the ionization of Cs is 95% complete, and plot percent completion
of ionization versus pressure ranging from 0 to 10 atm.
SOLUTION
Known: An equilibrium mixture of Cs, Cs
,e
is at 2000K. The value of the equilibrium constant at this temperature is
known.
Find: Determine the pressure of the mixture if the ionization of Cs is 95% complete. Plot percent completion versus pressure.
Assumption: Equilibrium can be treated in this case using ideal gas mixture equilibrium considerations.
Analysis: The ionization of cesium to form a mixture of Cs, Cs
, and e
is described by
where z denotes the extent of ionization, ranging from 0 to 1. The total number of moles of mixture n is
At equilibrium, we have so Eq. 14.35 takes the form
Solving for the ratio pp
ref
and introducing the known value of K
For p
ref
1 atm and z 0.95 (95%), p 1.69 atm. Using an equation-solver and plotting package, the following plot can
be constructed:
p
p
ref
115.632 a
1 z
2
z
2
b
K
1z2
1z2
11 z2
c
p
p
ref
11 z2
d
11 1
a
z
2
1 z
2
b a
p
p
ref
b
Cs
S
d
Cs
e
,
n 11 z2 z z 1 z
Cs S 11 z2Cs z
Cs
ze
Cs
S
d
Cs
e
z (%)
100
95
90
85
80
75
70
0246810
p (atm)
Figure E14.8
Figure E14.8 shows that ionization tends to occur to a lesser extent as pressure is raised. Ionization also tends to occur to
a greater extent as temperature is raised at fixed pressure.

14.4.4 Simultaneous Reactions
Let us return to the discussion of Sec. 14.2 and consider the possibility of more than one re-
action among the substances present within a system. For the present application, the closed
system is assumed to contain a mixture of eight components A, B, C, D, E, L, M, and N,
subject to two independent reactions
(14.24)
(14.46)
As in Sec. 14.2, component E is inert. Also, note that component A has been taken as com-
mon to both reactions but with a possibly different stoichiometric coefficient ( is not nec-
essarily equal to ).
The stoichiometric coefficients of the above equations do not correspond to the numbers
of moles of the respective components present within the system, but changes in the amounts
of the components are related to the stoichiometric coefficients by
(14.25a)
following from Eq. 14.24, and
(14.47a)
following from Eq. 14.46. Introducing a proportionality factor d
1
, Eqs. 14.25a may be rep-
resented by
(14.25b)
Similarly, with the proportionality factor d
2
, Eqs. 14.47a may be represented by
(14.47b)
Component A is involved in both reactions, so the total change in A is given by
(14.48)
Also, we have dn
E
0 because component E is inert.
For the system under present consideration, Eq. 14.10 is
(14.49)
Introducing the above expressions giving the changes in the n’s, this becomes
(14.50)
Since the two reactions are independent, d
1
and d
2
can be independently varied. Accord-
ingly, when dG]
T,p
0, the terms in parentheses must be zero and two equations of reaction
equilibrium result, one corresponding to each of the foregoing reactions
(14.26b)
(14.51)
n
A¿
m
A
n
L
m
L
n
M
m
M
n
N
m
N
n
A
m
A
n
B
m
B
n
C
m
C
n
D
m
D
ee
1n
A¿
m
A
n
L
m
L
n
M
m
M
n
N
m
N
2 de
2
dG4
T,p
1n
A
m
A
n
B
m
B
n
C
m
C
n
D
m
D
2 de
1
m
E
dn
E
m
L
dn
L
m
M
dn
M
m
N
dn
N
dG4
T,p
m
A
dn
A
m
B
dn
B
m
C
dn
C
m
D
dn
D
dn
A
n
A
de
1
n
A¿
de
2
dn
M
n
M
de
2
,
dn
N
n
N
de
2
dn
A
n
A¿
de
2
,
dn
L
n
L
de
2
e
dn
C
n
C
de
1
,
dn
D
n
D
de
1
dn
A
n
A
de
1
,
dn
B
n
B
de
1
e
dn
A
n
A¿
dn
L
n
L
dn
M
n
M
dn
N
n
N
dn
A
n
A
dn
B
n
B
dn
C
n
C
dn
D
n
D
n
A
n
A¿
122
n
A¿
A n
L
L
S
d
n
M
M n
N
N
112
n
A
A n
B
B
S
d
n
C
C n
D
D
702 Chapter 14 Chemical and Phase Equilibrium

14.4 Further Examples of the Use of the Equilibrium Constant 703
The first of these equations is exactly the same as that obtained in Sec. 14.2. For the case
of reacting ideal gas mixtures, this equation can be expressed as
(14.52)
Similarly, Eq. 14.51 can be expressed as
(14.53)
In each of these equations, the G term is evaluated as the change in Gibbs function for the
respective reaction, regarding each reactant and product as separate at temperature T and a
pressure of 1 atm.
From Eq. 14.52 follows the equilibrium constant
(14.54)
and from Eq. 14.53 follows
(14.55)
The equilibrium constants K
1
and K
2
can be determined from Table A-27 or a similar com-
pilation. The mole fractions appearing in these expressions must be evaluated by consider-
ing all the substances present within the system, including the inert substance E. Each mole
fraction has the form y
i
n
i
n, where n
i
is the amount of component i in the equilibrium
mixture and
(14.56)
The n’s appearing in Eq. 14.56 can be expressed in terms of two unknown variables through
application of the conservation of mass principle to the various chemical species present.
Accordingly, for a specified temperature and pressure, Eqs. 14.54 and 14.55 give two
equations in two unknowns. The composition of the system at equilibrium can be
determined by solving these equations simultaneously. This procedure is illustrated by
Example 14.9.
The procedure discussed in this section can be extended to systems involving several
simultaneous independent reactions. The number of simultaneous equilibrium constant ex-
pressions that results equals the number of independent reactions. As these equations are non-
linear and require simultaneous solution, the use of a computer is usually required.
n n
A
n
B
n
C
n
D
n
E
n
L
n
M
n
N
K
2
y
n
M
M
y
n
N
N
y
n
A¿
A
y
n
L
L
a
p
p
ref
b
n
M
n
N
n
A¿
n
L
K
1
y
n
C
C
y
n
D
D
y
n
A
A
y
n
B
B
a
p
p
ref
b
n
C
n
D
n
A
n
B
a
¢G
°
RT
b
2
ln c
y
n
M
M
y
n
N
N
y
n
A¿
A
y
n
L
L
a
p
p
ref
b
n
M
n
N
n
A¿
n
L
d
a
¢G°
RT
b
1
ln c
y
n
C
C
y
n
D
D
y
n
A
A
y
n
B
B
a
p
p
ref
b
n
C
n
D
n
A
n
B
d
EXAMPLE 14.9 Considering Equilibrium with Simultaneous Reactions
As a result of heating, a system consisting initially of 1 kmol of CO
2
, kmol of O
2
, and kmol of N
2
forms an equilibrium
mixture of CO
2
, CO, O
2
,N
2
, and NO at 3000 K, 1 atm. Determine the composition of the equilibrium mixture.
SOLUTION
Known: A system consisting of specified amounts of CO
2
,O
2
, and N
2
is heated to 3000 K, 1 atm, forming an equilibrium
mixture of CO
2
, CO, O
2
,N
2
, and NO.
1
2
1
2
704 Chapter 14 Chemical and Phase Equilibrium
Find: Determine the equilibrium composition.
Assumption: The final mixture is an equilibrium mixture of ideal gases.
Analysis: The overall reaction has the form
Applying conservation of mass to carbon, oxygen, and nitrogen, the five unknown coefficients can be expressed in terms of
any two of the coefficients. Selecting a and b as the unknowns, the following balanced equation results:
The total number of moles n in the mixture formed by the products is
At equilibrium, two independent reactions relate the components of the product mixture:
1.
2.
For the first of these reactions, the form taken by the equilibrium constant when p 1 atm is
Similarly, the equilibrium constant for the second of the reactions is
At 3000 K, Table A-27 provides log
10
K
1
0.485 and log
10
K
2
0.913, giving K
1
0.3273 and K
2
0.1222.
Accordingly, the two equations that must be solved simultaneously for the two unknowns a and b are
The solution is a 0.3745, b 0.0675, as can be verified. The composition of the equilibrium mixture, in kmol per kmol
of CO
2
present initially, is then 0.3745CO, 0.0675NO, 0.6255CO
2
, 0.6535O
2
, 0.4663N
2
.
If high enough temperatures are attained, nitrogen can combine with oxygen to form components such as nitric oxide.
Even trace amounts of oxides of nitrogen in products of combustion can be a source of air pollution.
0.3273
a
1 a
a
1 a b
4 a
b
1
2
,
0.1222
2b
311 a b2 11 b24
1
2
K
2
b
3
1
2
11 a b24
1
2
3
1
2
11 b24
1
2
c
1
14 a2
2
d
11
21
2
2b
311 a b2 11 b24
1
2
K
1
a3
1
2
11 a b24
1
2
11 a2
c
1
14 a2
2
d
11
21
a
1 a
a
1 a b
4 a
b
1
2
1
2
O
2
1
2
N
2
S
d
NO
CO
2
S
d
CO
1
2
O
2
n a b 11 a2
1
2
11 a b2
1
2
11 b2
4 a
2
1
CO
2
1
2
O
2
1
2
N
2
S a CO bNO 11 a2 CO
2
1
2
11 a b2 O
2
1
2
11 b2N
2
1 CO
2
1
2
O
2
1
2
N
2
S a CO bNO c CO
2
d O
2
eN
2
❶
PHASE EQUILIBRIUM
In this part of the chapter the equilibrium condition dG]
T, p
0 introduced in Sec. 14.1
is used to study the equilibrium of multicomponent, multiphase, nonreacting systems. The
discussion begins with the elementary case of equilibrium between two phases of a pure
substance and then turns to the general case of several components present in several
phases.
❶

14.5 Equilibrium Between Two Phases of a Pure Substance 705
Clapeyron equation
14.5 Equilibrium Between Two Phases of a
Pure Substance
Consider the case of a system consisting of two phases of a pure substance at equilibrium.
Since the system is at equilibrium, each phase is at the same temperature and pressure. The
Gibbs function for the system is
(14.57)
where the primes and denote phases 1 and 2, respectively.
Forming the differential of G at fixed T and p
(14.58)
Since the total amount of the pure substance remains constant, an increase in the amount
present in one of the phases must be compensated by an equivalent decrease in the amount
present in the other phase. Thus, we have dndn, and Eq. 14.58 becomes
At equilibrium, dG]
T,p
0, so
(14.59)
At equilibrium, the molar Gibbs functions of the phases are equal.
CLAPEYRON EQUATION. Equation 14.59 can be used to derive the Clapeyron equation, ob-
tained by other means in Sec. 11.4. For two phases at equilibrium, variations in pressure are
uniquely related to variations in temperature: p p
sat
(T ); thus, differentiation of Eq. 14.59
with respect to temperature gives
With Eqs. 11.30 and 11.31, this becomes
Or on rearrangement
This can be expressed alternatively by noting that, with Eq. 14.59 becomes
or
(14.60)
Combining results, the Clapeyron equation is obtained
(14.61)
Applications of the Clapeyron equation are provided in Chap. 11.
dp
sat
dT
1
T
a
h– h¿
v– v¿
b
s– s¿
h– h¿
T
h
¿ T s¿ h– T s–
g h T s,
dp
sat
dT
s– s¿
v– v¿
s¿ v¿
dp
sat
dT
s– v–
dp
sat
dT
0g
¿
0T
b
p
0g
¿
0p
b
T
dp
sat
dT
0g
–
0T
b
p
0g
–
0p
b
T
dp
sat
dT
g
¿ g–
dG4
T,p
1g¿ g– 2 dn¿
dG4
T, p
g¿ dn¿ g– dn–
G n¿g
¿ 1T, p2 n–g– 1T, p2
