Мироновский Л.А. Моделирование линейных систем Учебное пособие
Подождите немного. Документ загружается.

81
Подчеркнем, что метод интегрирующего множителя позволил
получить аналитическое описание фазовых траекторий, хотя ис-
ходное дифференциальное уравнение не интегрируется в элемен-
тарных функциях.
на рис. 3.13, г приведены четыре фазовые траектории для ма-
ятника с трением, описываемого уравнением
0
01 0 0, sin , .xx x x++ = =
они получены при запуске модели маятника из положения
покоя с начальной скоростью
0
1234,,,.x =
два первых случая
отвечают колебательному движению без переворота, два дру-
гих – движению с одним и двумя переворотами.
Пример 4. нелинейное дифференциальное уравнение второго
порядка вида
2
10()x x xxµ+ - +=
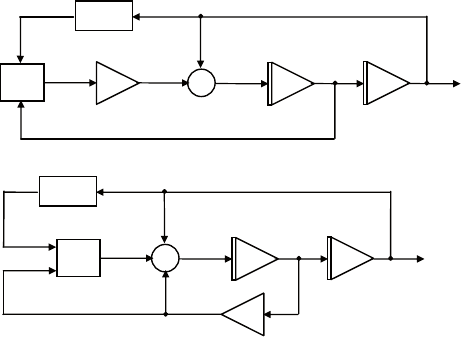
называется уравнением Ван-дер-Поля. два варианта его схемы
моделирования приведены на рис. 3.14, а, б.
каждая из схем содержит два интегратора, блок перемноже-
ния (помечен крестиком) и функциональный блок для реализа-
ции функции
2
1.x -
Рис. 3.14. Моделирование уравнения Ван-дер-Поля
Í
s
s
Í
s
s
2
1x -
x
x
´
´
2
1x -
б)
а)
82
схемы получены методом кельвина для следующих вариан-
тов записи исходного уравнения:
22
1( ), .x x xx x xx xxµ µµ=- - - =- + -
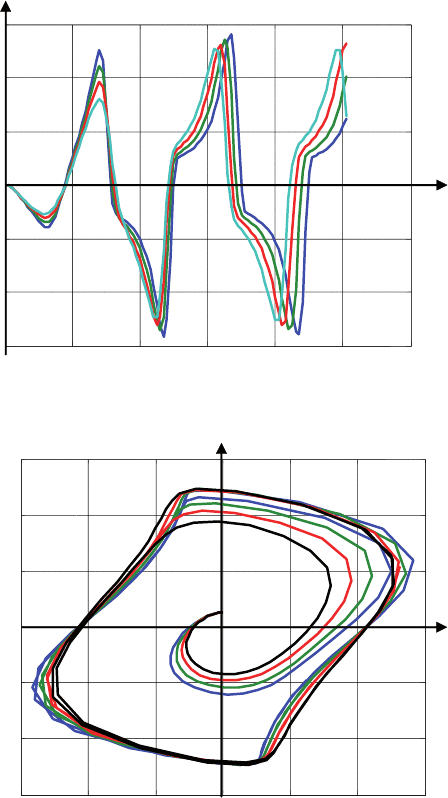
Рис. 3.15. Решения уравнения Ван-дер-Поля
s
s
Í
U
Рис. 3.16. Фазовый портрет
s s s
s
s
s
x
t

83
вид решений x(t) уравнения ван-дер-Поля при разных значе-
ниях параметра µ приведен на рис. 3.15, а на рис. 3.16 показана
траектория решения на фазовой плоскости
( , ).xx
на последнем
рисунке хорошо виден предельный цикл, соответствующий уста-
новившемуся режиму работы.
3.4. Моделирование системы дифференциальных
уравнений
наряду с дифференциальным уравнением вида (3.6) часто ис-
пользуют описание моделируемых объектов с помощью системы
дифференциальных уравнений первого порядка
11 0
01, () , , ,
i i in n i i
x ax a x x x i n= ++ = =
…
(3.9)
где x
i
– так называемые переменные состояния; a
ij
– постоянные
коэффициенты.
Матричная запись системы (3.9) имеет вид
0
, (0) ,==X AX X X
(3.10)
где Х – вектор-столбец с компонентами x
1
, …, x
n
; X
0
– вектор на-
чальных условий; A – квадратная матрица с элементами a
ij
.
например, при моделировании летательного аппарата состав-
ляющими вектора X могут быть текущие координаты самолета и
скорости их изменения, тогда матрица А будет характеризовать
динамику самолета.
если в матричном уравнении (3.10) отразить наличие вход-
ного и выходного сигналов, то получим стандартное описание в
пространстве состояний
,,uy=+ =X AX b cX
(3.11)
или в более подробной записи
1 11 1 1 1 1
1
1
d
..............
d
...
... ... ... , [ ... ] ... .
...
n
n
n n nn n n n
x a ax b x
u yc c
t
x a ax b x
éù é ùéù éù éù
êú ê úêú êú êú
êú ê úêú êú êú
= +=
êú ê úêú êú êú
êú ê úêú êú êú
ëû ë ûëû ëû ëû
квадратная матрица А, входящая в это описание, характери-
зует внутреннюю структуру системы и ее собственную динамику
(свободное движение), а матрицы b и c – структуру ее входного и
выходного устройств.
84
Матричному уравнению (3.11) соответствует блок-схема, со-
держащая блок интеграторов, блок сумматоров и блоки матрич-
ных усилителей (рис. 3.17).
для моделирования систем (3.9) или (3.11) методом кельвина
достаточно составить схемы для каждого уравнения отдельно и
соединить их между собой.
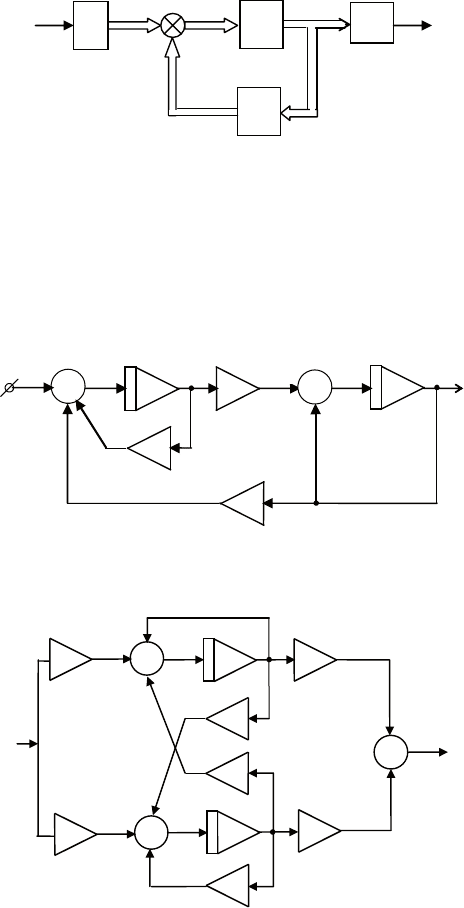
Рис. 3.17. Реализация системы в пространстве состояний
Z
C
D
®
V
9
CV
®
ò
Рис. 3.18. Схема моделирования для примера 5
Z
s
Z
s
s
Рис. 3.19. Схема моделирования для примера 6
Z
V
s
s
s
s
85
Пример 5. схема моделирования системы из двух дифферен-
циальных уравнений
1 1 2 2 12
32 5 6,y y y y yy= - + =- -
имеет вид, показанный на рис. 3.18. она содержит два интегра-
тора, два сумматора и три усилителя.
Пример 6. на рис. 3.19 показана схема моделирования объек-
та второго порядка, задаваемого уравнениями
1 24 5
25
3 18 2
, [ ].uy
é ù éù
--
ê ú êú
= +=
ê ú êú
--
ë û ëû
XX X
схема составлена непосредственно по уравнениям, она вклю-
чает два интегратора, три сумматора и семь усилителей для
умножения на постоянные коэффициенты (по числу неединич-
ных элементов матриц).
3.5. Эквивалентные схемы моделирования
Метод кельвина позволяет строить схемы моделирования
для линейных и нелинейных дифференциальных уравнений, а
также для систем таких уравнений. соответствующая методика
проста и достаточно универсальна. однако это не единственный
метод моделирования.
Фактически для каждого дифференциального уравнения
можно составить много схем, имеющих разную структуру – па-
раллельную, последовательную, цепную и др. с математической
точки зрения они будут эквивалентными, однако их технические
характеристики – сложность, вычислительная устойчивость,
удобство реализации – могут существенно различаться.
Поясним это на примере линейного дифференциального урав-
нения третьего порядка
210
0.yayayay+++=
(3.12)
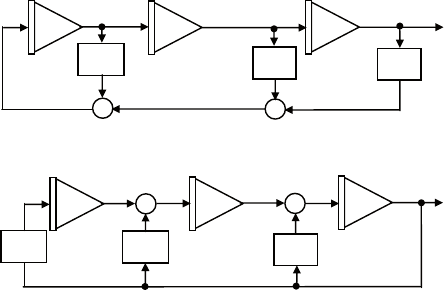
на рис. 3.20 приведены два варианта схемы моделирования
этого уравнения.
Первая из них построена по методу кельвина, вторая схема
представляет собой зеркальное отображение первой. она имеет
те же элементы и коэффициенты, но отличается направлением
прохождения сигналов, это так называемая дуальная схема.
86
чтобы доказать эквивалентность обеих схем, найдем диффе-
ренциальное уравнение для второй из них. обозначим выходные
сигналы интеграторов этой схемы через
123
,,xxx
и выпишем
дифференциальные уравнения для каждого интегратора:
1 2 21 2 3 11 3 01
, ,.x x ax x x ax x ax= - = - =-
(3.13)
исключим из этих уравнений переменные
23
,,xx
для чего
дважды дифференцируем первое уравнение с учетом двух других:
1 21 11 3
1 21 11 01
0
,
.
xaxaxx
xaxaxax
++=
+++=
(3.14)
Поскольку
1
,xy=
последнее уравнение совпадает с уравнени-
ем (3.12), следовательно, обе схемы эквивалентны и при установ-
ке согласованных начальных условий дадут один и тот же выход-
ной сигнал.
обозначим начальные условия исходного уравнения через
000
,,yyy
. тогда согласованные начальные условия схемы, при-
веденной на рис. 3.20, б, рассчитываются по формулам:
10 0 20 0 2 0 30 0 2 0 1 0
,, ,x y x yayx yayay= =+ =+ +
которые вытекают из уравнений (3.13), (3.14) при
0.t =
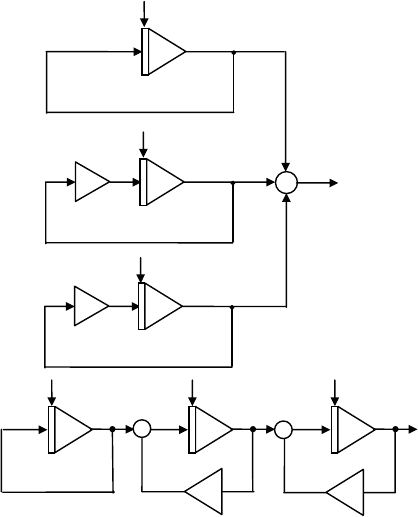
два других варианта моделирования дифференциального
уравнения (3.12) – параллельная и последовательная схемы – по-
казаны на рис. 3.21.
Рис. 3.20. Дуальные схемы
s¸
s¸
s¸
Z
sB
sB
sB
Y
Í
Z
Y
y
y
б)
а)
87
они отвечают случаю, когда исходное дифференциальное
уравнение (3.12) имеет вид
4 60y yy y+ +- =
с начальными условиями
00 0
3 4 14, ,.yy y= =- =
корни характеристического полинома в этом случае веще-
ственны
12 3
123,,,pp p= =- =-
им соответствует решение
23
() .
ttt
yt e e e
--
=+ +
в параллельной схеме (рис. 3.21, а) каждое из слагаемых ре-
шения формируется отдельной схемой и результаты складыва-
ются.
в последовательной схеме (рис. 3.21, б) на выходах интеграто-
ров будут сигналы
Рис. 3.21. Параллельная (а) и последовательная (б) схемы
для уравнения (3.12)
U
F
U
F
s
s
U
F
s
s
Z
Í
Í
Ë
s
s
б)
а)
88
2 23
12
12 4,, .
t tt ttt
x ex ee yee e
- --
= = + =+ +
таким образом, обе схемы (рис. 3.21) при указанных началь-
ных условиях эквивалентны в смысле равенства их выходных
сигналов.
кроме четырех приведенных вариантов схем моделирования
дифференциального уравнения (3.12) можно предложить и дру-
гие, например параллельно-последовательные, цепные и т. д.
определенную проблему при этом составляет пересчет началь-
ных условий при переходе от одной эквивалентной схемы к дру-
гой. на практике лучше выбирать наиболее простую схему, либо
схему, отвечающую физическому смыслу задачи.
Пример 7. Построим эквивалентные схемы моделирования
для системы, рассмотренной в примере 6. она описывается урав-
нениями
11 2
2 12
12
24 5
3 18 2
25
,
,
.
x x xu
x x xu
yx x
=- + -
=- - +
=+
(3.15)
схема моделирования, построенная непосредственно по этим
уравнениям, приведена на рис. 3.19.
чтобы получить другие варианты схем, перейдем к диффе-
ренциальному уравнению второго порядка относительно пере-
менной у. дважды продифференцируем последнее из уравнений
(3.15), подставляя в него вместо
12
,xx
правые части двух первых
уравнений:
12
12
12
25
17 42
143 348
,
,
.
yx x
y xx
y x xu
=+
=- -
=-+
домножив первое уравнение на 90, второе – на 19 и сложив
с третьим:
19 90 ,y y yu++=
(3.16)
получим дифференциальное уравнение второго порядка, описы-
вающее исходную систему. схема его моделирования методом
кельвина показана на рис. 3.22, а.
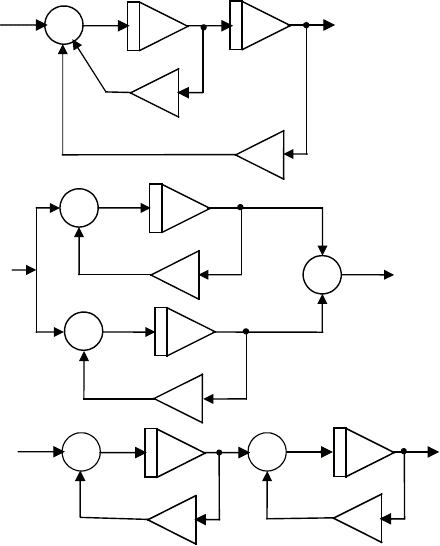
на рис. 3.22, б приведен параллельный вариант схемы моде-
лирования этого уравнения. найдем дифференциальное урав-
89
нение для ее выходного сигнала. он определяется равенством
12
,yy y=-
где выражения для
1
y
и
2
y
имеют вид
1 12 2
9 10,.yuy yu y=- =-
дважды продифференцировав равенство для у с учетом этих
выражений, получим
12
12
12
9 10
81 100
,
,
.
yy y
yy y
y y yu
=-
=- +
=- - +
домножим первое уравнение на 90, второе – на 19 и сложим
их с третьим. результатом будет уравнение (3.16), что доказыва-
ет эквивалентность двух первых схем (см. рис. 3.22, а, б).
Рис. 3.22. Три варианта схемы для примера 7
V
s
s
V
s
s
Z
s
Z
Z
Z
V
s
s
Z
б)
а)
в)
90
Аналогичный анализ последовательного варианта схемы, по-
казанной на рис. 3.22, в, также приводит к уравнению (3.16).
таким образом, все три приведенных варианта эквивалентны.
каждый из них требует всего два умножения на постоянные ко-
эффициенты в отличие от исходной схемы (см. рис. 3.19), тре-
бующей семь умножений. они более просты и удобны для моде-
лирования, чем исходный.
Задачи и упражнения
1. определить, при каких значениях а и при каких началь-
ных условиях решение уравнения
0x ax x+ +=
имеет вид:
а) x = sint, б) x = cost, в) х = e
t
,
г) х = e
–t
, д) х = e
3t
, е) х = e
t/3
.
2. в чем заключается метод кельвина (метод понижения про-
изводной)? Пользуясь этим методом, составить схемы моделиро-
вания для всех вариантов п. 1.
3. Привести схемы моделирования в SIMULINK следующих
дифференциальных уравнений:
а)
00
9 0 1 0;,,xx x x+= = =
б)
00
0 5 0 1, sin , .x x x xx+ + = ==
4. используя метод кельвина, составить схемы моделирова-
ния следующих дифференциальных уравнений:
а)
10 0 0 0 15;, () ()x xx-= = =
б)
0 0 1;, () ()x xx x= = =-
в)
2 7 8 0 10 0 5 0 3;, () , () , ()xxx x x x+ + =- =- =- =
г)
54
0 0 0 0 0 0 0 20
() ()
, () () () () , () .x xxxx x= ==== =-
5. схема моделирования представляет собой кольцо из трех
интеграторов с единичными коэффициентами и одинаковыми
начальными условиями. найти моделируемое дифференциаль-
ное уравнение и его аналитическое решение.
6. Процесс нагревания теплоизолированного стержня описы-
вается системой дифференциальных уравнений
210000 1
1 21 0 0 0 0
0 1 21 0 0 0
0 0 1 21 0 0
0001 21 0
00001 1 0
.u
é ù éù
-
ê ú êú
ê ú êú
-
ê ú êú
ê ú êú
-
ê ú êú
=+
ê ú êú
-
ê ú êú
ê ú êú
-
ê ú êú
ê ú êú
-
ê ú êú
ë û ëû
XX
