Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

12 2

.T T y T y ky ku+ +=

 

решая это дифференциальное уравнение, можно найти реак-

цию следящей системы на любое входное воз-

действие.

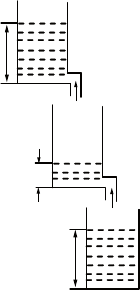
Резервуары с жидкостью. рассмотрим за-

дачу о протекании жидкости через три сооб-

щающихся сосуда (рис. 2.5). обозначим уров-

ни жидкости в сосудах через x

(t), x

(t)

и будем считать, что в начальный момент вре-

мени жидкость была только в первом сосуде,

т. е. х

(0) = m, х

(0) = х

(0) = 0. очевидно, что

с течением времени х

будет убывать, а х

–

возрастать. Уровень х

сначала будет расти, а

затем, начиная с некоторого момента времени

, уменьшаться.

Полагая скорость вытекания жидкости

пропорциональной ее количеству, получаем,

что процесс может быть описан системой трех дифференциаль-

ных уравнений

1 11 1

2 11 22 2

3 22 3

0 0

, () ,

, () .

x kx x m

x kx kx x

x kx x

=- =



(2.7)

Левые части уравнений (2.7) соответствуют скоростям изме-

нения уровней жидкости в сосудах, положительные и отрица-

тельные слагаемые в правых частях уравнений характеризуют

количество прироста и убыли жидкости. например, слагаемое

во втором уравнении отражает приток жидкости во второй

сосуд из первого, а слагаемое –k

отражает ее вытекание из

второго сосуда в третий.

Уравнения (2.7) можно переписать в матричной форме

11 1

212 2

3 23

0 00

00 0

, () .

xk x m

xkk x

x kx

éùé ùéù éù

êúê úêú êú

=- =

êúê úêú êú

ëûë ûëû ëû



(2.8)

эту модель можно усложнить, учитывая возможность по-

полнения жидкости в первом сосуде и вытекания ее из третьего

сосуда.

Рис. 2.5. Три

резервуара









Приведенные примеры показывают, что математические мо-

дели в виде линейных дифференциальных уравнений естествен-

ным образом возникают в различных прикладных областях. они

относятся к числу стандартных средств описания физических и

технических объектов и процессов.

следующий этап моделирования связан с аналитическим или

численным решением дифференциальных уравнений. общих

методов решения нелинейных дифференциальных уравнений не

существует. остановимся на аналитических методах решения

линейных дифференциальных уравнений.

2.3. Решение линейных дифференциальных уравнений

2.3.1. Свойства линейных дифференциальных уравнений

дифференциальное уравнение вида

1 10

() ( )

() () () () ()

xtax t axtaxtft

+ ++ + =…

(2.9)

называется линейным дифференциальным уравнением n-го по-

рядка с постоянными коэффициентами. если возмущающая

функция f(t) равна нулю, то уравнение называется о дн о р о д -

н ы м, в противном случае – н е о д н о ро д ны м . решением урав-

нения (2.9) является любая функция х(t), удовлетворяющая

ему. для каждого уравнения (2.9) существует целый класс таких

функций.

отметим три свойства решений линейного однородного диф-

ференциального уравнения

1 10

() ( )

x a x ax ax

+ ++ + =…

(2.10)

Свойство 1. если х

(t) и х

(t) – два решения уравнения (2.10),

то функция х

(t) = с

(t) + с

(t), где с

и с

– любые постоян-

ные коэффициенты, также является решением уравнения (2.10).

это свойство в технике известно как принцип суперпозиции для

однородных систем.

Свойство 2. существует n различных линейно независимых

решений уравнения (2.10).

Свойство 3. общее решение уравнения (2.10) имеет вид х

(t) =

= с

(t) + … + с

(t), где х

(t), …, х

(t) – линейно независимые

решения уравнения (2.10); с

, …, с

– произвольные коэффици-

енты.

отметим теперь два свойства неоднородного уравнения (2.9).

Свойство 4. общее решение уравнения (2.9) равно сумме

какого-либо частного решения х

(t) и общего решения соответ-

ствующего однородного уравнения х

(t)

х(t) = х

(t) + х

(t) = с

(t) + … + с

(t) + х

(t).

Свойство 5. если х

(t) и х

(t) – решения уравнения (2.9) с пра-

выми частями f

(t) и f

(t) соответственно, то х

(t) + х

(t) будет

решением уравнения

1 1 0 12

() ( )

() () () () () ().

xtax t axtaxtftft

+ ++ + = +…

это свойство является принципом суперпозиции для неодно-

родных систем.

таким образом, общее решение дифференциального урав-

нения n-го порядка зависит от n произвольных постоянных х

= х(t, с

, …, с

)

Придавая постоянным с

, …, с

числовые значе-

ния, будем получать различные частные решения дифференци-

ального уравнения.

Пример 1. Уравнение малых колебаний математического ма-

ятника

0xx+=

 

(2.11)

имеет решение x = sint. в самом деле, подставляя x = sint и

sinxt=-

 

в уравнение, получим тождество. Аналогично показы-

вается, что x = соst также является решением этого уравнения.

согласно свойству 1 функция х(t) = с

sint + с

cost будет реше-

нием уравнения (2.11) при любых с

и с

. эта формула определя-

ет общее решение.

для выбора конкретного решения необходимы дополнитель-

ные условия. найдем, например, решение уравнения (2.11), про-

ходящее через точку

01(),x =

03().x =



Подставляя эти значения

в общее решение, получим

1212

1 0 03 0 0sin cos , cos sin .cccc=+=-

отсюда с

= 3, с

= 1, т. е. искомое решение имеет вид х = 3sint +

+ cost.

в случае уравнения порядка n нужно задать n дополнитель-

ных условий. обычно ими являются значения решения и его

производных в некоторые моменты времени. если все n усло-

вий относятся к одному моменту времени, то они называются

начальными условиями. задача решения дифференциально-

го уравнения с начальными условиями известна как задача

коши. зная общее решение уравнения и начальные условия

00 0

()

( ), ( ), ..., ( ),

xt x t x t

легко найти постоянные с

, …, с

, по-

добно тому, как это было сделано в примере 1.

кроме задачи коши часто рассматривают краевую задачу,

когда заданы значения решения и его производных в различные

моменты времени. например, для уравнения (2.11) можно за-

дать

01 2 1() , ( /) .xxπ= =-

тогда постоянные с

и с

находятся из

соотношений

12 1

1 0 01

sin cos , sin cos ,cc c

ππ

= + -= +

откуда с

= –1, с

= 1, и решение имеет вид х(t) = – sint + cost.

2.3.2. Решение однородного дифференциального уравнения

рассмотрим аналитические методы решения линейного диф-

ференциального уравнения n-го порядка. одним из наиболее

распространенных является метод, основанный на нахождении

корней характеристического полинома.

Пусть дано однородное линейное дифференциальное уравне-

ние с постоянными коэффициентами (2.10) и начальными усло-

виями

01 1

0 0 0

()

( ) , ( ) , ..., ( ) .

xxxx x x

== =



будем искать решение в виде

xe=

. Подставив

xe=

уравнение (2.10) и сократив на

получим характеристиче-

ское уравнение

1 10

p a p ap a

+ +¼+ + =

(2.12)

если р

, …, р

– корни этого уравнения и среди них нет крат-

ных, то общее решение уравнения (2.10) согласно свойству 3

имеет вид

() .

pt pt

xt ce c e= ++…

(2.13)

таким образом, для получения аналитического решения тре-

буется:

– записать характеристическое уравнение;

– определить его корни p

, …, p

;

– найти общее решение уравнения (2.13);

– используя начальные условия, определить значения коэф-

фициентов с

, …, с

наибольшую трудность в этой процедуре вызывает нахожде-

ние корней характеристического уравнения, так как при п > 4 не

существует формул для их определения.

Пример 2 (простые вещественные корни). дано уравнение

40.xx-=



выписываем характеристическое уравнение: р

– 4 = 0.

его корни р

= 2, р

= –2, поэтому общее решение представляет со-

бой сумму двух экспонент:

() .

xt ce ce

если среди корней характеристического уравнения имеются

кратные корни, то соответствующее слагаемое в общем решении

умножается на полином

c ct ct

+ +¼+

где k – кратность

корня.

Пример 3 (кратные вещественные корни). найдем аналитиче-

ское решение дифференциального уравнения

4520y yyy+++=

  

с начальными условиями у

= 1, у

= y

= 0.

среди корней характеристического уравнения

4 5 20ppp+ + +=

имеются два одинаковых корня р

= р

= –1, p

= –2. в этом случае общее решение записывается в виде

12 3

() ( ) .

yt c cte c e

=+ +

для определения произвольных постоянных дважды диффе-

ренцируем полученную функцию:

12 2 3

() ( ) ,

() ( )

yt c c t c e c e

=- + + -

=+ - +





и полагаем t равным нулю. в результате получаем три алгебраи-

ческих уравнения относительно коэффициентов с

, с

+ с

= 1, –с

+ с

– 2с

= 0, с

– 2 с

+ 4с

= 0.

решая их, находим значения коэффициентов: с

= 0; с

= 2;

= 1. окончательный вид решения:

2() .

y t te e

среди корней характеристического уравнения могут быть

комплексные корни. Пара сопряженных комплексных корней

12,

piαβ=±

приводит к появлению в решении слагаемых вида

sin cos .

ce t ce t

αα

ββ+

Пример 4 (комплексные корни). дано дифференциальное

уравнение

220.xxx++=

 

его характеристическое уравнение

+ 2р + 2 = 0 имеет корни

.pi=- ±

общее решение будет следующим:

( ) sin cos .

xt ce t ce t

При использовании описанного способа требуется знать соот-

ветствие между корнями характеристического уравнения и ре-

шениями дифференциального уравнения. в табл. 2.1 приведено

восемь типичных случаев такого соответствия.

Таблица 2.1

Соответствие корней и решений

№ п/п вид корней характер решения

0p =

p α=

12,

pjβ=±

sin cosc tc tββ+

12,

pjαβ=±

( sin cos )

ec tc t

ββ+

pp p= =¼= =

c ct ct

+ +¼+

12 k

pp pα= =¼= =

()

c ct ct e

α-

+ +¼+

12 34

2 12

,kk

pjβ

= =¼=

= =±

12 2

( )sin

( )cos

kk k

c ct ct t

c c t ct t

+ +¼+ +

+ + +¼+

12 34

2 12

,kk

pjαβ

= =¼=

= =±

12 2

( ) sin

( ) cos

kk k

c ct ct e t

c c t ct e t

+ +¼+ +

+ + +¼+

Пример 5. Пусть требуется найти решение дифференциально-

го уравнения

0xxxx+++=

  

с начальными условиями

00 0

40 35 50,, .xx x== =

 

его характеристическое уравнение

10ppp+ + +=

имеет

корни

1 23

,.p pi=- =±

общее решение будет следующим:

12 3

( ) sin cos .

xt ce c t c t

=+ +

После подстановки начальных условий получаем:

45 80 5( ) sin cos .

xt e t t

=+ +

в пакете MATLAB это решение может быть получено с помо-

щью команды dsolve:

x = dsolve(‘D3x + D2x + Dx + x = 0’, ‘x(0) = 50, Dx(0) = 35, D2x(0) = 40’)

Пример 6. Пусть известны корни характеристического урав-

нения шестого порядка:

1 2 3 4 56

0 2 34

,, .ppp p p i= = = = =- ±

они соответствуют второй, третьей и четвертой строкам

табл. 2.1. общее решение имеет вид

22 3 3

12 3 4 5 6

44( ) sin cos .

tt t

xt c ct ct ce ce t ce t

=+ + + + +

для определения произвольных постоянных в случае ком-

плексных корней приходится брать повторные производные от

функций

cos

ye t

β=

sin .

ye t

β=

в табл. 2.2 приведены фор-

мулы для производных до третьего порядка.

Таблица 2.2

Производные от гармонических функций

Производные от функции

cos

ye t

β=

cos

ye t

β=

( cos sin )

ye t t

αβββ-



2( cos sin cos )

ye t t t

α β αβ β β β= --



3 2 23

33( cos sin cos sin )

ye t t t t

αβαββαββββ= --+



Производные от функции

sin

ye t

β=

sin

ye t

β=

( sin cos )

ye t t

αβββ=+



2( sin cos sin )

ye t tb t

α β αβ β β= +-



3 2 23

33( sin cos sin cos )

ye t t t t

α β α β β αβ β β β= +--



Продолжить таблицу не составит труда, поскольку числовые

коэффициенты в ней совпадают по величине с коэффициентами

бинома ньютона, закон чередования их знаков также достаточно

очевиден.

Пример 7. требуется решить дифференциальное уравнение

65432

2 4 4 5 2 20

() () () () ()

y y y y y yy

++++++=

с заданными начальными условиями:

2 3 45

00 02 0 2 0 1 00 01

() () () ()

() , () , () , () , () , () .yy y y y y

= = =- =- = =

выписываем характеристический полином и факторизуем

его:

6 5 4 3 2 2 22

2 4 4 5 22 22 1( )( ) .pppppp ppp+ + + + ++= ++ +

находим его корни

,pj=- ±

34 56,,

.pp j= =±

они соответ-

ствуют четвертой и седьмой строкам табл. 2.1. следовательно,

общее решение имеет вид

1 2 34 56

( ) sin cos ( )sin ( )cos

yt ce t ce t c ct t c ct t

= + ++ ++

для учета начальных условий это выражение надо пять раз

продифференцировать (здесь поможет табл. 2.2) и положить

t = 0. После определения произвольных постоянных получаем

решение

( ) sin cos .

yt e t t t

2.3.3. Решение неоднородного дифференциального уравнения

Пусть дано неоднородное линейное дифференциальное урав-

нение (2.9). согласно свойству 4, для отыскания его общего ре-

Окончание табл. 2.2

шения х(t) сначала надо найти общее решение х

(t) соответству-

ющего однородного уравнения, а также какое-либо частное ре-

шение х

(t) неоднородного уравнения и сложить их:

х(t) = х

(t) + х

(t).

для получения х

(t), как и ранее, составляем характеристи-

ческое уравнение и находим его корни. частное решение диффе-

ренциального уравнения определяется видом правой части f(t)

дифференциального уравнения (2.2). если f(t) = 1, его следует

искать в виде константы х

= d. если в правой части стоит экс-

поненциальная функция f(t) = e

–t

, то частное решение нужно ис-

кать в виде экспоненты х

= de

–t

несколько типичных случаев приведены в табл. 2.3. в ней

слева указан вид функции f(t), а справа – рекомендуемая форму-

ла для поиска частного решения х

(t).

Таблица 2.3

частные решения для функций f(t)

f(t) х

(t)

b bt bt+ ++…

sin cosb tb tββ+

sin cos

be t be t

αα

ββ+

d dt dt+ ++…

sin cosd td tββ+

sin cos

de t de t

αα

ββ+

константы d

находят, подставляя х

(t) в уравнение (2.9) и

приравнивая коэффициенты при одинаковых функциях време-

ни в правой и левой частях.

Пример 8. возьмем уравнение

49.

x x te-=



общее решение соответствующего однородного уравнения

î1 2

() .

x t ce ce

частное решение ищем в виде

÷ 01

() ( ) .

x t d dte=+

Подставляя

()xt

в исходное уравнение и сокращая на

по-

лучим

101 01

2 49( ).d d dt d dt t++ - + =

Приравниваем коэффициенты при одинаковых степенях

t в правой и левой частях:

10 1

2 3 03 9,.dd d- =- =

отсюда

23,.dd=- =-

следовательно, x

(t)= – (2 + 3t)e

, и общее ре-

шение имеет вид

( )

23() .

tt t

xt ce ce te

= + -+

П р им е ч а н и е . возможны случаи, когда подстановка част-

ного решения, рекомендованного табл. 2.3, окончится неудачей

(приведет к несовместной системе уравнений). это бывает, когда

функция f(t) (или ее компоненты) удовлетворяют однородному

дифференциальному уравнению. в таких случаях следует попро-

бовать умножить частное решение на полином от t.

Пример 9. дано дифференциальное уравнение первого по-

рядка

2 .

x xe



Попытка найти частное решение вида

x de

приводит к

равенству

2 22

22 ,

t tt

de de e

- --

-+=

выполнение которого невозможно.

делаем вторую попытку, взяв

x dte

теперь подстанов-

ка в исходное уравнение дает:

2 2 22

22 ,

t t tt

de dte dte e

- - --

-+=

откуда

1.d =

следовательно, общее решение имеет вид

() .

x t ce te

в технических приложениях для решения дифференциаль-

ных уравнений часто используют операторный метод, основан-

ный на преобразовании Лапласа. согласно этому методу интегри-

рование дифференциальных уравнений сводится к алгебраиче-

скому решению соответствующих операторных уравнений. Пе-

реход к искомому решению осуществляется с помощью таблиц.

Пример 10. найдем реакцию звена с передаточной функцией

()

на входной сигнал x = coswt, если k = 2, T = 1 c,

w = 1 c

–1