Михайлова Т.В. Техническая термодинамика
Подождите немного. Документ загружается.


⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
υ
υ
p
dT
d
T
=0, то и α=0, а значит и ΔТ=0.
Итак, при некоторой строго определенной температуре реального газа
также, как и у идеального газа, его температурный эффект дросселирования
может оказаться равным нулю (α=0) и, следовательно,
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
h
dp
dT
и Т
1
=Т
2
=const,
т.е. температура реального газа при дросселировании при этом не изменяется.
Такое состояние, в котором температурный эффект дросселирования реального
газа равен нулю и меняет свой знак, называется точкой инверсии. Температура
реального газа, отвечающая точке инверсии, называется температурой
инверсии Т
инв
.
Из основного определения температурного эффекта дросселирования по
уравнению (13.7)
h
dp
dT
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
α
следует, что существует не одна, а множество точек инверсии, в зависимости от
величины давления p движущегося реального газа. Эти точки инверсии
определяются уравнениями
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
h
dp
dT
;
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
υ
υ
p
dT
d
T
=0; α=0. (13.13)
При этих условиях Т
1
=Т
2
= Т
инв
=const.
Совокупность точек инверсия, в которых α=0, представляет собой
непрерывную кривую, называемую кривой инверсии данного реального
вещества.
Исследования показывают, что температурный эффект дросселирования в
критической точке К имеет для всех веществ положительное значение α
к
>0.
Следовательно, дросселирование вещества в области критической точки
приводит всегда к понижению его температуры (ΔТ
к
)
при дросс
<0.
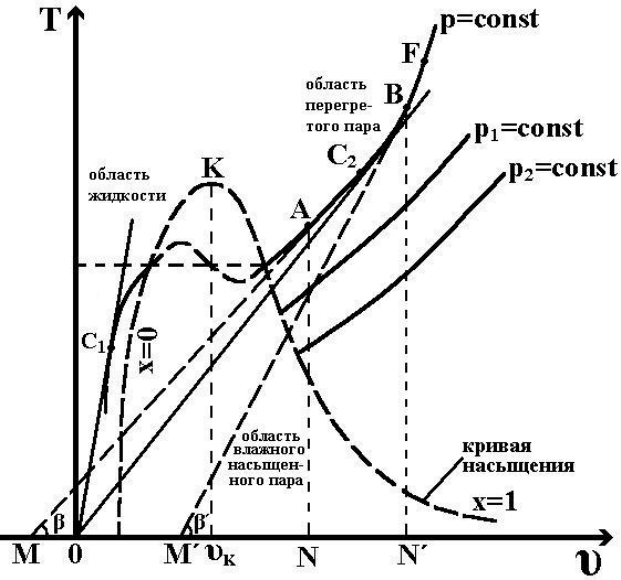
Основные соотношения, характеризующие особенности процесса
дросселирования, могут быть установлены графическим методом при
применении Тυ- диаграммы.
С помощью уравнения Ван-дер-Ваальса и при известных критических
параметрах реального газа или пара (р
к
, υ
к
, Т
к
) можно построить Тυ- диаграмму
состояния вещества. Если в этой диаграмме провести изобару реального газа
или пара вплоть до жидкого состояния, то получим следующий вид диаграммы
(рис. 13.3). Проведем анализ процесса дросселирования реального газа с
помощью этой диаграммы.
Рис. 13.3
Пусть при заданном давлении р осуществляется процесс дросселирования
этого газа. Рассмотрим два случая дросселирования.
Первый случай отвечает начальному состоянию реального газа перед
дросселированием, характеризуемому точкой А, и второй случай – точкой В.
Линия C
1
-A-C
2
-B-F представляет собой изобару p=const данного
реального газа. Через эту точку A начального состояния реального газа
проведем касательную к изобаре и определим значение отрезка MN:

MN
AN
d
dT
tg
p
=
⎟
⎠
⎞
⎜
⎝
⎛
=
υ
β
, (13.14)
отрезок AN отвечает текущему значению температуры Т в точке A, т.е. AN= Т.
Отрезок MN можно представить в виде суммы двух отрезков
MN=MO+ON=MO+υ, т.к. ON=υ (текущее значение объема), то, следовательно,
p
d
dT
МО
Т
tg
⎟
⎠
⎞
⎜
⎝
⎛
=
+
=
υυ
β
.
Отсюда имеем
()
p
d
dT
МОТ
⎟
⎠
⎞
⎜
⎝
⎛
+=
υ
υ
.
Тогда
υ
υ
−
⎟
⎠
⎞
⎜
⎝
⎛
=
p
dТ
d
ТМО
. (13.15)
Таким образом, отрезок MO соответствует положительному значению
числителя в уравнении (13.8)
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
υ
υ
p
dT
d
TМО
>0.
Из предыдущего анализа уже было выяснено, что если числитель
выражения (13.8) положителен, то и температурный дроссель-эффект
положителен (α>0), а следовательно, ΔТ<0, т.е. в этом случае имеет место
понижение температуры реального газа при дросселировании.
Для точки B соответственно получим
NM
NВ
d
dT
tg
p
′′
′
=
⎟
⎠
⎞
⎜
⎝
⎛
=
′
υ
β
.
Отрезок BN´ равен текущему значению температуры Т в точке B, т.е. BN´=Т, из
рис. 13.3 следует, что
M´N´=ON´-OM´.
Отрезок ON´ равен текущему значению объема υ в точке B.
ON´=υ.
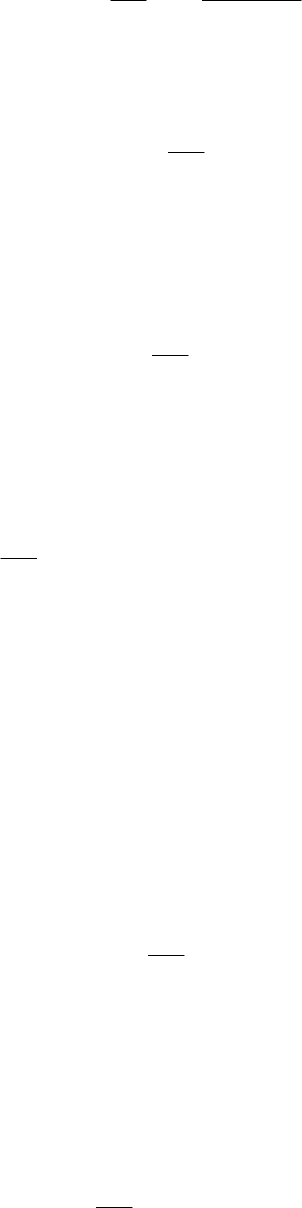
Следовательно,
M´N´=υ-OM´,
MО
Т
d
dT
tg
p
′
−
=
⎟
⎠
⎞
⎜
⎝
⎛
=
′
υυ
β
.
Отсюда получаем, что
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
′
υ
υ
p
dT
d
TМО
, (13.16)
т.е. отрезок OM´ соответствует значению числителя в уравнении (13.8), но с
противоположным знаком:
0<
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
′
υ
υ
p
dT
d
TМО
.
Из предыдущего анализа было выяснено, что если числитель выражения (13.8)
отрицателен
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
υ
υ
p
dT
d
T
<0, то и α<0, а ΔТ>0,
т.е. в этом случае имеет место увеличение температуры реального газа при
дросселировании.
Из приведенного выше анализа можно сформулировать следующее
положение.
Если точка M лежит левее начала координат в системе [Т, υ] (случай A,
рис. 13.3), то числитель уравнения (13.8)
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
υ
υ
p
dT
d
T
>0
и при дросселировании имеет место понижение температуры реального газа.
Если же точка M´ располагается правее начала координат в системе
[Т, υ] (случай B, рис. 13.3), то числитель уравнения (13.8)
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
υ
υ
p
dT
d
T
<0, а ΔТ>0,
т.е. в этом случае температура реального газа в процессе дросселирования
повышается.
Если же точки M или M´ совпадают с началом координат, то
следовательно,
0=
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
υ
υ
p
dT
d
TМО
,
а значит, согласно уравнению (13.8) α=0.
В этом случае температура реального газа при дросселировании, как и у
идеального газа, не изменяется и соответствует температуре инверсии, а само
состояние газа при этом отвечает точке инверсии. Из графика на рис. 13.3
видно, что для любой изобары реального газа отвечают этому условию две
точки инверсии C
1
и C
2
: одна в области перегретого пара - C
2
, а другая в
области жидкости - C
1
.
Рис. 13.4
Так как для различных изобар имеет место свое значение температуры
инверсии, то, следовательно, как уже было указано, температура инверсии
зависит от давления и в координатах p, t можно изобразить сплошную кривую
инверсии. Инверсионная кривая для азота представлена на рис. 13.4. В области,
лежащей выше инверсионной кривой, температурный эффект ΔТ>0, т.е.
дросселирование вызывает нагревание газа, а в области, лежащей под
инверсионной кривой, температурный эффект ΔТ<0 отрицателен, т.е.
дросселирование газа сопровождается его охлаждением. Согласно
вышеизложенному, каждому давлению отвечают две точки инверсии, т.е. две
температуры, в которых температурный эффект дросселирования равен нулю.
Первая точка, соответствующая меньшей температуре, называется
нижней инверсионной точкой, а вторая, соответствующая большей
температуре - верхней инверсионной точкой.
Кривая инверсии пересекается с осью температур в двух точках А и B
(т.е. прямой p=0, рис. 13.4). В точке B пересечения правой ветви кривой
инверсии с осью температур объем υ→∞, а температура Т
2
в этой точке для
газа, подчиняющегося уравнению Ван-дер-Ваальса, будет равна
к
ТТ 75,6
2
0
=
. (13.17)
Т
к
– критическая температура данного газа. Левая ветвь инверсионной кривой
пересекается с осью температур в точке А. Для газа, подчиняющегося
уравнению Ван-дер-Ваальса, значение температуры инверсии в этой точке
будет равно
к
ТТ 75,0
1
0
=
. (13.18)
Конечно, эти величины и , полученные для Ван-дер-Ваальсовских газов,
лишь приближенно отвечают реальным данным, поскольку само уравнение
Ван-дер-Ваальса является приближенным.
1
0
Т
2
0
Т
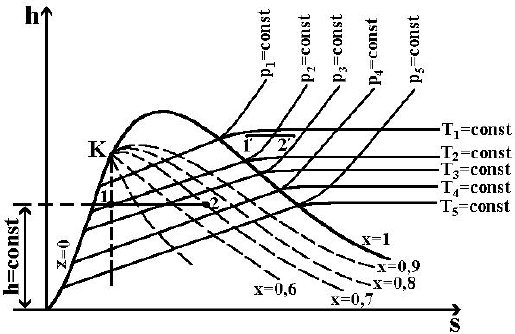
Если рассмотреть процесс дросселирования паров и проанализировать его
по hs- диаграмме, то можно
прийти к следующим выводам.
Дросселирование паров в hs- диаграмме изображено на рис. 13.5.
Рис. 13.5

Дросселирование влажных насыщенных паров большой степени
влажности (малых значений х) приводит к увеличению степени сухости х таких
паров и одновременному значительному понижению температуры этого пара
(процесс 1-2 рис. 13.5). При этом влажный пар подсушивается. Этот эффект
значительного понижения температуры при дросселировании влажных паров
используется в современной холодильной технике для получения холода
(положительный эффект Джоуля-Томсона). То же самое наблюдается и при
дросселировании перегретого пара, но в значительно меньшей степени (процесс
1´-2´, рис. 13.5).
Контрольная карточка 13.2
Укажите наиболее полный и правильный ответ
Вопрос Ответ
1. При дросселировании идеального газа Т
1
... 1. =Т
2
;
2.
>Т
2
;
3.
<Т
2
;
4.
>
<
Т
2
.
2. При дросселировании реального газа или
пара Т
1
...
1. =Т
2
;
2.
>Т
2
;
3.
<Т
2
;
4.
>
<
Т
2
.
3. Температурный эффект дросселирования α
идеального газа
1.
>
<
0;
2.
>0;
3.
<0;
4. =0.
4. Температурный эффект дросселирования α
реального газа и пара
1.
>
<
0;
2.
>0;
3.
<0;
4. =0.
5. Степень сухости при дросселировании
паров большой степени влажности…
1. не изменяется;
2. уменьшается;
3. увеличивается.
6. Эффект Джоуля–Томсона проявляется при
дросселировании…
1. идеального газа;
2. реального газа;
3. любого газа.
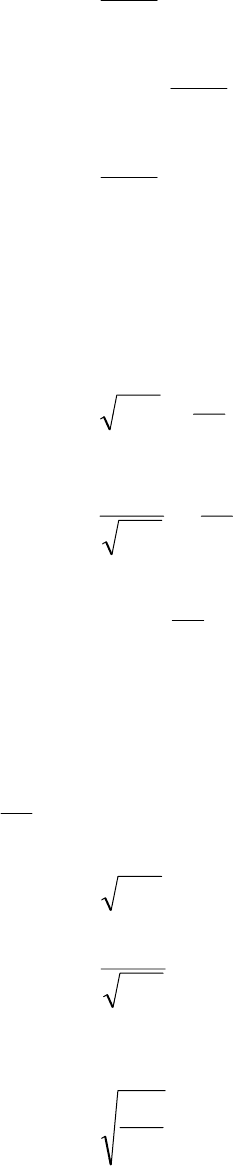
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Укажите правильное выражение первого закона термодинамики для
адиабатного потока газа, текущего по горизонтальному неподвижному каналу
без трения.
1.
()
0
2
2
=+++
тех
dlpddu
dW
υ
;
2. 0
2
2
=+
dW
dp
υ
;
3.
0
2
2
=+ dh
dW
.
2. Укажите правильную структурную формулу для скорости истечения W газа
из сопла (индекс 1, 2 относятся к входному и выходному сечениям
соответственно).
1.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
2
1
p
p
fRT
;
2.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
2
1
1
p
p
f
RT
p
;
3.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
2
1
p
p
fRT
.
3. Укажите правильную зависимость расхода газа m, вытекающего из сопла, от
давления р
1
и температуры Т
1
на входе при заданной геометрии и отношении
1
2
p
p
.
1.
1
RT
;
2.
1
1
RT
p
;
3. ;
1
RT
4.
1
1
RT
p
.
4. Давление газа на входе в расчетное сопло Лаваля р
1
=20 бар, давление
окружающей среды р
н
=5 бар. Чему равно давление р
2
на срезе сопла?
1. 5,28 бар;
2.
5 бар;
3. 10,56 бар;
4.
Недостаточно данных
5. Давление воздуха на входе в сужающееся сопло р
1
=40 бар, давление
окружающей среды р
н
=2,5 бар. Чему равно давление р
2
на срезе сопла?
1. 2,5 бар;
2.
21,12 бар;
3. 5,28 бар;
4.
40 бар
6. Давление воздуха на входе в сужающееся сопло р
1
=6 бар, давление
окружающей среды р
н
=4,5 бар. Чему равно давление р
2
на срезе сопла?
1. 4,5 бар;
2.
5,28 бар;
3.
3,17 бар;
4. 6,0 бар.
7. Укажите правильную зависимость скорости истечения W от отношения
давлений
1
p
p
н
=
β
для сужающегося сопла (α), расчетного сопла Лаваля (δ).
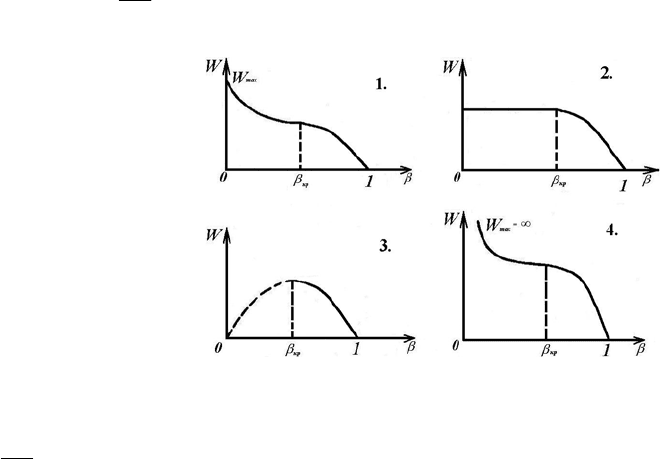
8. Укажите правильную зависимость расхода газа m от отношения давления
1
p
p
н
=
β
для сужающегося сопла (α) и сопла Лаваля (δ).
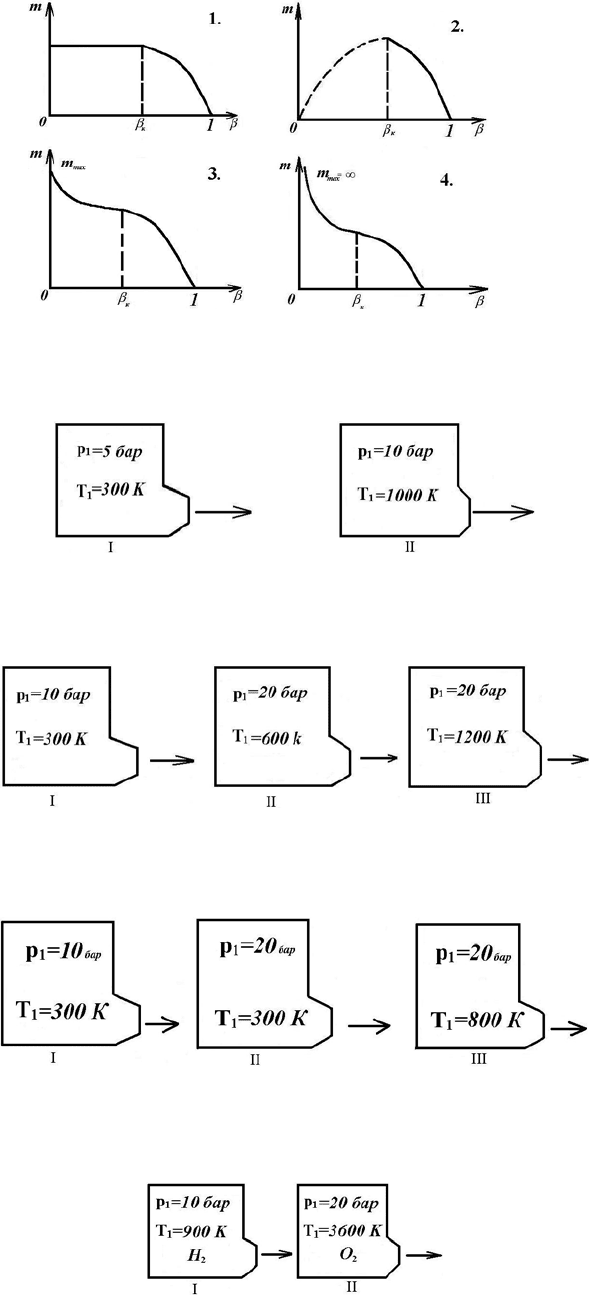
9. Сравните скорость W и m при истечении воздуха через одинаковые
сужающиеся сопла, р
н
=1бар.
10. Сравните расхода m при истечении CO
2
через одинаковые сужающиеся
сопла, р
н
=1 бар.
11. Сравните скорости истечения газа через одинаковые сужающиеся сопла,
р
н
=1 бар.
12. Сравните скорости W и расход m при истечении газов (H
2
и O
2
) из
одинаковых сужающихся сопел, р
н
=1 бар.
1. W
1
=W
2
; m
1
<m
2
;
2. W
1
>W
2
; m
1
<m
2
;
3. W
1
<W
2
; m
1
>m
2
;
