Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


42-10
REFERENCE DATA FOR ENGINEERS
computers use a total of
32
bits or more for the
mantissa, exponent, and sign fields.
Many computers use a “single precision” floating-
point format developed by the IEEE Standards Com-
mittee. This format uses a 24-bit mantissa and an 8-bit
exponent to represent signed numbers with absolute
values in the range of about 2-Iz7 to
2’12’
to
The IEEE standard also specifies a 64-bit
(‘‘double precision”) format and gives guidelines for
extended formats (e.g., 128-bit “quad precision” for-
mat).
Computer systems may use either of two methods to
provide floating-point operations. Some computers
have built-in hardware and instructions to process
floating-point numbers in a prescribed format. Others
have software programs that operate
on
floating-point
numbers using sequences of primitive arithmetic in-
structions. The hardware approach typically performs
operations
100
times faster than the software approach.
A computer that “supports” floating-point numbers
is one that provides a minimum set of floating-point
instructions including addition, subtraction, multiplica-
tion, division, and comparison of floating-point num-
bers, and conversion to and from integer fixed-point
format. Special algorithms are needed to perform these
instructions, including scaling or “normalization” of
operands and results, as well as arithmetic manipula-
tions of mantissas and exponents.
BCD
Representation
The
binary-coded decimal
(BCD)
number system
encodes the digits
0
through
9
by their 4-bit unsigned
binary representations,
0000
through 1001. The codes
1010
through
1
11
1
are not used. Conversions between
BCD and decimal representations are trivial, a direct
substitution of four bits for each decimal digit. Two
BCD digits may be packed into one byte; thus one byte
may represent the values from
0
to
99
as opposed to
0
to
255
for a normal unsigned 8-bit binary number. Binary-
coded decimal numbers with any desired number of
digits may be obtained by using a string of bytes, one
byte for each two digits.
Computers “support” BCD representation by pro-
viding instructions that perform arithmetic on packed-
BCD numbers. Some computers have a “decimal
adjust” instruction that corrects the result of an ordi-
nary 8-bit add instruction, assuming that the operands
were packed-BCD bytes. Others have decimal add,
subtract, multiply, and divide instructions that operate
directly on packed-BCD bytes, words,
or
arbitrary-
length strings of bytes.
Character Codes
A string of bits in a computer need not represent a
number;
in
fact most input and output
of
contemporary
computers is nonnumeric. The most common type
of
nonnumeric data is
text,
strings of characters from
some character set. Each character is represented in the
computer by a bit string according to an established
convention.
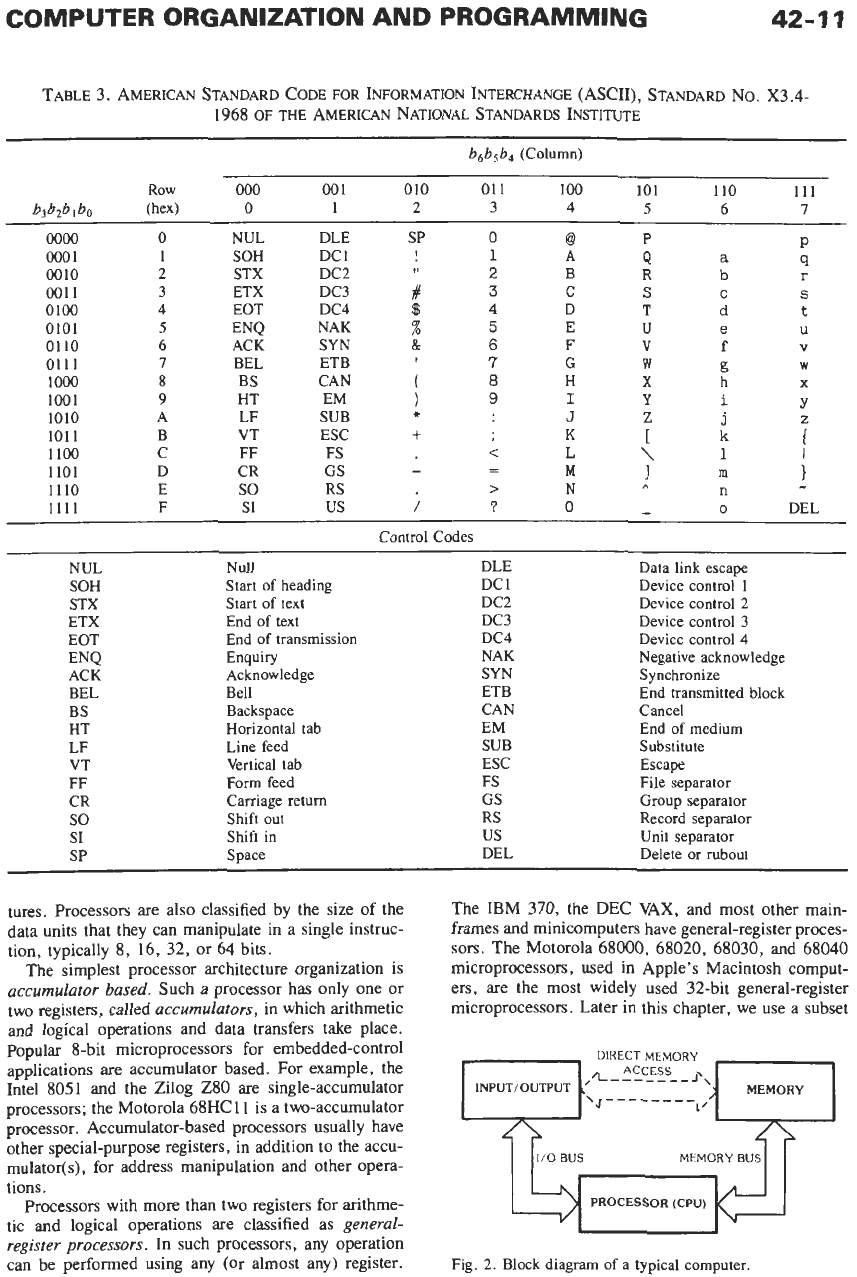
The most commonly used character code is ASCII,
the American Standard Code for Information Inter-
change. This code represents each of 128 different
characters by a 7-bit string, as shown in Table
3.
Thus,
the text string “Yeccch!” is represented by a rather
innocent looking list of seven 7-bit numbers:
1011001 1100101 1100011 1100011 1100011
1101o000100001
Some
of
the 7-bit strings in ASCII denote device
control functions instead of “printing” characters. For
example, CR (0001 101) returns the print head
or
cursor
on a printer or display toL the first column, and LF
(0001010) advances to the next line. Most of the other
control characters are intended for use by data commu-
nication links, but different computer systems may use
these characters for different functions.
Most computers manipulate
an
8-bit quantity as a
single unit, a byte, and store one character in each byte.
The disposition of the extra bit when 7-bit ASCII is
used depends on the system
or
program. Sometimes
this bit is set to a particular value, sometimes it is
ignored, and sometimes it is used to encode an addi-
tional 128 non-ASCII characters.
An important feature of ASCII is that the bit strings
for letters and digits form a reasonable numerical
sequence,
so
that text strings can be sorted by computer
instructions that compare numerical values.
BASIC COMPUTER
ORGANIZATION
A computer system consists of three major subsys-
tems: processor, memory, and input/output
(UO),
as
shown in Fig.
2.
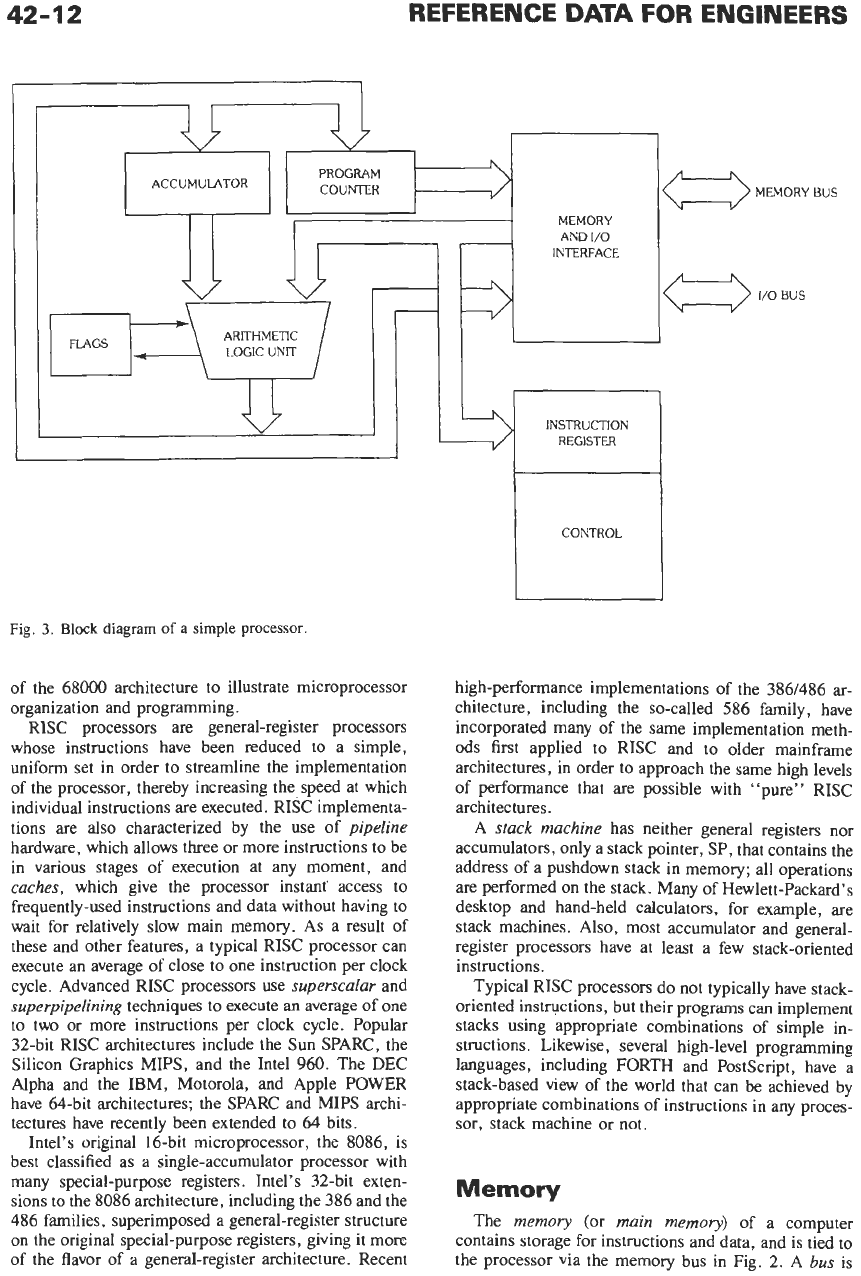
Processors
The
processor
(or
central processing unit,
CPU)
is
the heart of the computer. Shown in Fig.
3,
a simple
processor contains control circuits for fetching and
executing instructions, an arithmetic logic unit
(ALU)
for manipulating data, and registers for storing proces-
sor status and a small amount of data. It
also
has
interface circuits for controlling and communicating
with the memory and
YO
subsystems.
Different processors have different organizations,
both in their internal implementations and
in
their
architectures as seen by programmers. Typical organi-
zations can be roughly classified as accumulator-based
processors, general-register processors, and stack ma-
chines. Recently,
a
number
of
new general-register
processor architectures have employed principles
of
reduced instruction-set computing
(RISC)
to
obtain
performance advantages over older processor architec-
TABLE
3.
AMERICAN STANDARD CODE
FOR
INFORMATION
INTERCHANGE
(ASCII), STANDARD
NO.
X3.4-
1968
OF
THE
AMERICAN NATIONAL STANDARDS INSTITUTE
~~
b6b5b,
(Column)
Row
000
00
1
010
01
1
100
101
110
111
bibzbibo
(hex)
0
1
2
3
4
5
6
7
0000
000
1
0010
001
1
0100
0101
01
10
0111
1000
1001
1010
1011
1100
1101
1110
1111
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
NUL
SOH
STX
ETX
EOT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
DLE
DC
1
DC2
DC3
DC4
NAK
SY
N
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
SP
/
0
1
2
3
<
-
-
>
?
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
0
P
Q
R
S
T
U
V
W
X
Y
Z
[
\
1
A
-
a
b
C
d
e
f
g
h
i
j
k
1
n
m
0
P
q
r
S
t
u
V
W
X
Y
z
DEL
Control
Codes
NUL
SOH
STX
ETX
EOT
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
SP
ENQ
Null
Start
of
heading
Start
of
text
End
of
text
End of
transmission
Enquiry
Acknowledge
Bell
Backspace
Horizontal tab
Line
feed
Vertical
tab
Form
feed
Carriage return
Shift out
Shift
in
Space
DLE
DC
1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
DEL
Data
link
escape
Device control
1
Device control
2
Device
control
3
Device control
4
Negative acknowledge
Synchronize
End transmitted block
Cancel
End of medium
Substitute
Escape
File separator
Group separator
Record separator
Unit
separator
Delete or rubout
tures. Processors are also classified by the size of the
data units that they can manipulate in a single instruc-
tion, typically
8,
16, 32, or 64 bits.
The simplest processor architecture organization is
accumulator based.
Such a processor has only one or
two registers, called
accumulators,
in which arithmetic
and logical operations and data transfers take place.
Popular 8-bit microprocessors for embedded-control
applications are accumulator based. For example, the
Intel 8051 and the Zilog Z80 are single-accumulator
processors; the Motorola 68HC 1 1 is a two-accumulator
processor. Accumulator-based processors usually have
other special-purpose registers, in addition to the accu-
mulator(s), for address manipulation and other opera-
tions.
Processors with more than two registers for arithme-
tic and logical operations are classified as
generul-
register processors.
In such processors, any operation
can be performed using any (or almost any) register.
The IBM 370, the DEC VAX, and most other main-
frames and minicomputers have general-register proces-
sors. The Motorola
68000,
68020, 68030, and 68040
microprocessors, used in Apple’s Macintosh comput-
ers, are the most widely used 32-bit general-register
microprocessors. Later in this chapter, we use a subset
DIRECT MEMORY
INPUTIOUTPUT
‘4
- -
-
-
- -
-
-
~
PROCESSOR (CPU)
Fig.
2.
Block
diagram
of
a
typical computer.
42-12
REFERENCE
DATA
FOR ENGINEERS
AND
I/O
INTERFACE
I
CONTROL
Fig.
3.
Block
diagram
of
a
simple processor.
of the 68000 architecture to illustrate microprocessor
organization and programming.
RISC processors are general-register processors
whose instructions have been reduced to a simple,
uniform set in order to streamline the implementation
of the processor, thereby increasing the, speed at which
individual instructions are executed. RISC implementa-
tions are
also
characterized by the use of
pipeline
hardware, which allows three or more instructions to be
in various stages
of
execution at any moment, and
caches,
which give the processor instant‘ access to
frequently-used instructions and data without having to
wait for relatively slow main memory. As a result of
these and other features, a typical RISC processor can
execute an average
of
close to one instruction per clock
cycle. Advanced RISC processors use
superscalar
and
superpipelining
techniques to execute an average of
one
to
two or more instructions per clock cycle. Popular
32-bit RISC architectures include the Sun SPARC, the
Silicon Graphics MIPS, and the Intel 960. The DEC
Alpha and the IBM, Motorola, and Apple POWER
have 64-bit architectures; the SPARC and MIPS archi-
tectures have recently been extended to 64 bits.
Intel’s original 16-bit microprocessor, the 8086, is
best classified as a single-accumulator processor with
many special-purpose registers. Intel’s 32-bit exten-
sions to the 8086 architecture, including the 386 and the
486 families, superimposed a general-register structure
on the original special-purpose registers, giving it more
of the flavor of a general-register architecture. Recent
INSTRUCTION
REGISTER
a
MEMORY
BUS
c3
I/O
BUS
high-performance implementations of the 386/486 ar-
chitecture, including the so-called 586 family, have
incorporated many of the same implementation rneth-
ods first applied to RISC and to older mainframe
architectures, in order to approach the same high levels
of performance that are possible with “pure” RISC
architectures.
A
stack machine
has neither general registers nor
accumulators, only a stack pointer, SP, that contains the
address of
a
pushdown stack in memory; all operations
are
performed on the stack. Many of Hewlett-Packard’s
desktop and hand-held calculators, for example, are
stack machines. Also, most accumulator and general-
register processors have at least a few stack-oriented
instructions.
Typical RISC processors do not typically have stack-
oriented ins-ctions, but their programs can implement
stacks using appropriate combinations of simple in-
structions. Likewise, several high-level programming
languages, including FORTH and PostScript, have a
stack-based view of the world that can be achieved by
appropriate combinations
of
instructions in any proces-
sor, stack machine or not.
Memory
The
memory
(or
main memory)
of a computer
contains storage for instructions and data, and is tied to
the processor via the memory bus in Fig. 2. A
bus
is

42-13
simply a bundle of wires or any other physical medium
for transferring information. A computer memory has
some number of
locations,
each
of
which stores a b-bit
quantity. In most contemporary computers, each loca-
tion stores an 8-bit
byte.
Associated with each location
in the memory is a unique binary number called the
address.
If there
are
n
locations, then the addresses
range from
0
to
n
-
1.
The key feature that distinguishes main memory
from other forms of storage in a computer is
random
access-the processor has equally fast access to every
location in memory. Random access memory is analo-
gous to a wall of post office boxes; a postal clerk can
deposit mail in any box with equal ease. Compare this
with the
serial access
method of a letter carrier who
visits locations sequentially, in the order
of
the route.
Magnetic tapes provide serial-access memory in com-
puter systems.
Fig.
4
shows how the processor accesses main
memory
in a typical small computer system. The
memory is an array of
n
locations of
b
bits each. To read
the data stored at location
X,
the processor places the
number
X
on the address bus, and activates a read
control signal; the memory responds by placing the
contents of location
X
on the data bus. To write a value
V
at location
X,
the processor places
X
on the address
bus and
V
on the data bus and activates Write; the
memory immediately writes the value
V
in the specified
location. Subsequent reading of address
X
will now
return the value
V.
Fig. 5A provides a conceptual view
of
a memory
with 216 bytes; a 16-bit address uniquely specifies any
byte in this memory. Larger memories use more
address bits.
Fig.
5B
shows the physical memory organization
used in 32-bit Motorola 68000-family microprocessors.
Notice that although the memory is 32 bits
(4
bytes)
wide, each byte has its own address. Also, more bytes
(232) can be addressed, since addresses are 32 bits wide.
In the 68000 memory, a 16-bit
word
is defined as two
consecutively numbered bytes, and a 32-bit
long
word
is
four consecutive bytes. For example, “word 2” consists
of bytes 2 and
3,
and “long word 4” consists of bytes
4
through
7.
A
word whose address is a multiple of two,
or a long word whose address is a multiple
of
4,
is
said
to be
aligned.
Fig. 5C shows the physical memory organization
used in 32-bit Intel 80x86 microprocessors (the 80386
and its successors). The memory organization is similar
to that of the 68000 family, except that the byte
numbering within a word is reversed. (Somehow, it is
befitting that the 68x and x86 families should have their
byte order reversed!)
A
4-byte quantity in the
80x86
is called a
double
word.
The 80x86 allow words and double words to be
nonaligned.
For example, “word
7”
in Fig. 5C consists
of bytes
7
and
8,
with byte
7
occupying the most
significant position in the word. However, aligned
words can usually be accessed in physical memory
faster than nonaligned ones.
Note that “word” doesn’t mean the same thing in all
processor architectures. For example, in most RISC
architectures, “word” refers to a 32-bit quantity, and a
16-bit quantity is called a
halfword.
Several types of memories are commonly used in
computer main memory systems. With a
readiwrite
memory
(RWM),
a processor can store data at any
address and read back the stored information at any
time. Most semiconductor RWMs are
volatile,
in that
the stored information disappears when power is re-
moved,
With a
read-only memory
(ROM),
a processor can
read the contents of any address at any time, but data
values can be stored only once, when the ROM is
manufactured. The key advantage of a ROM is that
it
is
a
nonvolatile;
that is, its contents are preserved even if
no power is applied.
A
programmable read-only memory
(PROM)
is
simi-
lar to a ROM, except that the customer may store data
values (Le., “program the PROM”) using a
PROM
programmer.
A
PROM chip is manufactured with all its
bits at a particular value, typically
1.
The PROM
programmer can be used to set desired bits to the
opposite value. In PROMS that use bipolar technology,
MAIN
MEMORY
ADDRESS
0
1
2
3
n-2
n-
1
DATA
BUS
Fig.
4.
Main
memory
in
a typical computer

42-14
0000
0001
0002
0003
0004
REFERENCE DATA FOR ENGINEERS
1
-
-
-
-
-
-8-
64
KBMES
FFFD
FFFE
FFFF
(A)
Byte-addressable
memory
for
an 8-bit processor
Fig.
5.
Memory
organizations.
4
32
c
00000000
00000004
00000008
oooooooc
FFFFFFE8
FFFFFFEC
FFFFFFFO
FFFFFFF4
FFFFFFFB
FFFFFFFC
4
GIGABWES
(B)
Byte-addressable memory
/or
0
32-blt
processo
(0
“B1g
Endlan”
such
as
the Motorola
680WI
this is typically done by vaporizing tiny fuses inside the
PROM corresponding to each bit. In MOS PROMS, this
is typically done by forcing electrons into tiny insulated
wells corresponding to each
0
bit, where they can
rem& trapped for
10
years or more.
An
erasable programmable read-only memory
(EPROM)
is similar to a PROM, except that the EPROM
can be “erased” to the all-1’s state by exposing it to
ultraviolet light. An
electrically erasable programmable
read-only
memory
(EEPROM or E2PROM)
is
similar to
an EPROM, except that it may be erased electrically.
Every computer has RWM for storing variable data.
Depending on the computer and the application, the
programs may also be stored in RWM, or they may be
stored in ROM, PROM, EPROM, or EEPROM. Storing
programs in EEPROM is especially advantageous in
embedded-control applications, since software can
be
updated (for example, via modem) without requiring
the chip to be physically replaced.
All of the memories described above
are
rundom-
access memories,
because the processor has equally fast
access
to
every memory location. However, computer
jargon has developed
so
that the acronym “RAM”
most commonly refers
to
read/write memory only.
Input/Output
The
inputlourput
(itOJ
subsystem of
a
computer
contains
peripheral devices
for communicating with,
observing, and controlling the world outside the com-
puter. Peripheral devices include terminals, printers,
communication devices, and mechanical sensors and
actuators. Also included in the
YO
subsystem are
muss
storage devices
such as magnetic tapes and disks. These
devices are used to store information not needed in the
main memory at all times, such as applications pro-
grams and text files. Not all computers have mass
storage devices, but all useful computers have at least
one peripheral device, since by definition a peripheral is
-
32
-
00000000
00000004
00000008
oooooooc
FFFFFFE8
FFFFFFEC
FFFFFFFO
FFFFFFF4
FFFFFFF8
FFFFFFFC
(C)
Alternative byte-oddressoble memory
for
LI
3Zbit
procewr
(a
so-called “Llttle Endlan”
such as the Intel
803%).
the only means for the computer to communicate with
the outside world.
The processor writes and reads information to and
from peripherals by means of
UO
instructions that place
commands and data on the
I/O
bus.
In
many computers,
both main memory and peripherals share the same
physical
bus.
Going one step further, some processors
communicate with their peripherals using registers that
masquerade as memory locations. In such computer
systems, the processor makes no distinction between
accessing main memory and accessing peripherals.
In simple computer systems, there is no direct path
from peripherals to main memory; the only way to
transfer data between a peripheral and memory is for the
processor to read it from the peripheral and store it in
memory, or vice versa. However, systems requiring a
higher data transfer rate incorporate
direct
memory
access
(DMA),
a link between a special peripheral
controller and memory that allows a peripheral to read
and write memory without processor intervention.
PROCESSORS
AND
PROGRAMMING
The Motorola 68000 microprocessor family, used
in
Apple’s Macintosh computers, contains several differ-
ent microprocessor chips that share a common base
architecture. The
68000
architecture is an excellent
example of a general-register processor, and we’ll use it
to introduce general concepts
of
processor architecture
and assembly-language programming in this section.
Organizal
General-I
ion
of
a
legister Processor
Fig. 6 shows the conceptual organization of a typical
68000-family processor. This processor accesses a
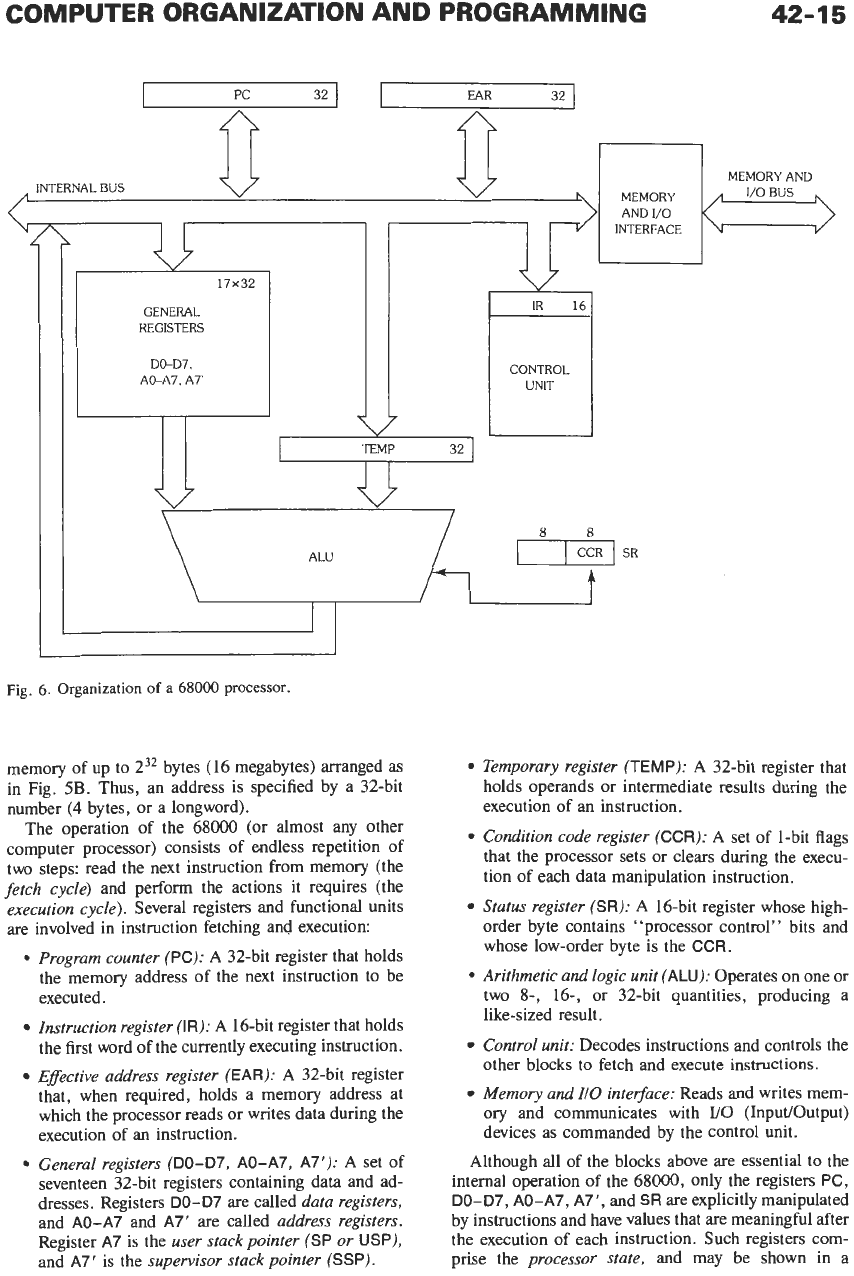
COMPUTER ORGANIZATION AND PROGRAMMING
PC 32
42-15
EAR 32
MEMORY AND
INTERNAL
BUS
”
17x32
GENERAL
REGISTERS
DCLD7,
AO-A7. A7
f?
CONTROL
L
uu
Fig.
6.
Organization
of
a
68000
processor.
memory of up to 232 bytes (16 megabytes) arranged as
in Fig.
5B.
Thus, an address is specified by a 32-bit
number
(4
bytes, or a longword).
The operation of the 68000 (or almost any other
computer processor) consists of endless repetition of
two steps: read the next instruction from memory (the
fetch cycle)
and perform the actions it requires (the
execution cycle).
Several registers and functional units
are involved in instruction fetching and execution:
Program counter
(PC):
A
32-bit register that holds
the memory address of the next instruction to be
executed.
Instruction register
(IR):
A
16-bit register that holds
the first word
of
the currently executing instruction.
Effective address register
(EAR):
A 32-bit register
that, when required, holds a memory address at
which the processor reads or writes data during the
execution of an instruction.
General registers
(DO-D7, AO-A7, A7’):
A
set of
seventeen 32-bit registers containing data and ad-
dresses. Registers
DO-D7
are called
data registers,
and
AO-A7
and
A7‘
are
called
address registers.
Register
A7
is
the
user stack pointer
(SP
or
USP),
and
A7‘
is
the
supervisor stack pointer
(SSP).
Temporary register
(TEMP):
A
32-bit register that
holds operands or intermediate results during the
execution of
an
instruction.
Condition code register
(CCR):
A
set of 1-bit flags
that the processor sets or clears during the execu-
tion of each data manipulation instruction.
Status register
(SR):
A
16-bit register whose high-
order byte contains “processor control” bits and
whose low-order byte is the
CCR.
*
Arithmetic and
logic
unit
(ALU):
Operates on one or
two
8-,
16-, or 32-bit quantities, producing a
like-sized result.
Control unit:
Decodes instructions and controls the
Memory and
110
integace:
Reads and writes mem-
ory
and communicates with
YO
(InpuUOutput)
devices as commanded by the control unit.
Although all of the blocks above are essential to the
internal operation of the 68000, only the registers
PC,
DO-D7, AO-A7, A7’,
and
SR
are
explicitly manipulated
by instructions and have values that are meaningful after
the execution of each instruction. Such registers com-
prise the
processor state,
and may be shown in a
other blocks to fetch and execute instructions.

42-16
I
I I
programming model
for the processor, as in Fig.
7.
Only
these registers are of concern to a programmer.
DO
Instruction Formats
For the purposes of illustration, we introduce a subset
of the complete 68000 instruction set. Instructions in
the subset are one to four words long.
The first word of each instruction is called the
opcode
word.
It contains an operation code
(opcode)
and zero,
one, or two
efective-address
(EA)
jields.
The opcode
uniquely specifies the operation to be performed, while
each
EA
field specifies the register or memory location
that contains an
operand
to be manipulated by the
instruction.
If an operand is a variable stored in memory, then an
additional instruction word may be used in computing
the address of the memory location. If the operand is an
“immediate” constant, then one or two additional
instruction words may contain the constant value.
As
shown in Fig. 8, the instructions in the subset use
six different formats for the opcode word, as required
by different operations and operand types. There are
many other formats used by the full 68000 instruction
set.
To
understand why a particular set of formats is used
in a given processor architecture, one must understand
I
I
I I
1
I
! !
I
I
I
I
I
I
I
I
the goals, optimizations, and compromises of the
architects, which is beyond the scope of this chapter.
When you look at the formats in Fig. 8, you will often
ask, “Why did they do
that?”
This question
is
easier to
answer in view of the full 68000 instruction set, because
there are many more instructions to be encoded, but
even the full set of 68000 instructions is encoded
somewhat irregularly.
In RISC architectures, instruction formats
are
quite a
contrast from those of the 68000. A hallmark of RISC
architecture is that all instructions have the same, fixed
width (one word), and there are very few distinct
instruction formats. This greatly simplifies and speeds
up instruction fetching and decoding.
Returning to the 68000, most of its data-manipula-
tion instructions can operate on bytes, words, or
longwords. The operand size is encoded as part
of
the
opcode in
MOVE
instructions (Fig. SA) and in the size
or
op-mode
field in other instructions (Figs. 8B and
8C).
Instructions that reference memory contain a 6-bit
EA
field that specifies the location of the operand;
MOVE
contains two such fields. In all of these instruc-
tions, the
EA
field can specify one
of
several “address-
ing modes” as discussed shortly. Some addressing
modes require an additional word of addressing infor-
mation to be appended to the instruction, thus giving
rise to two-
to
four-word instructions.
~.
D1
D2
D3
D4
D5
D6
D7
I
I
I
I
A0
A1
A2
A3
I
I
I
I
A4
A5
Ah
t
A7(SP/USP)
I
I
I
A7‘ISSP)
31
24
23
20
19
0
15
13
10
9
8
43210
I
I
I
I
I
PC
I
T
Kd
s
wyA
12
I
11
I
10
p//
’y/A
X
1
N
I
Z
I
V
I
Cl
SR
CCR
Fig.
7.
Programming
model
for
the
68000.

42-17
opcode dst
EA
src
EA
opcode reg op-mode src
or
dst
EA
(A)
MOVE.
(Bl
Other
double-operand
opcode size dst
EA
I
opcode
dst
EA
Instruction Set
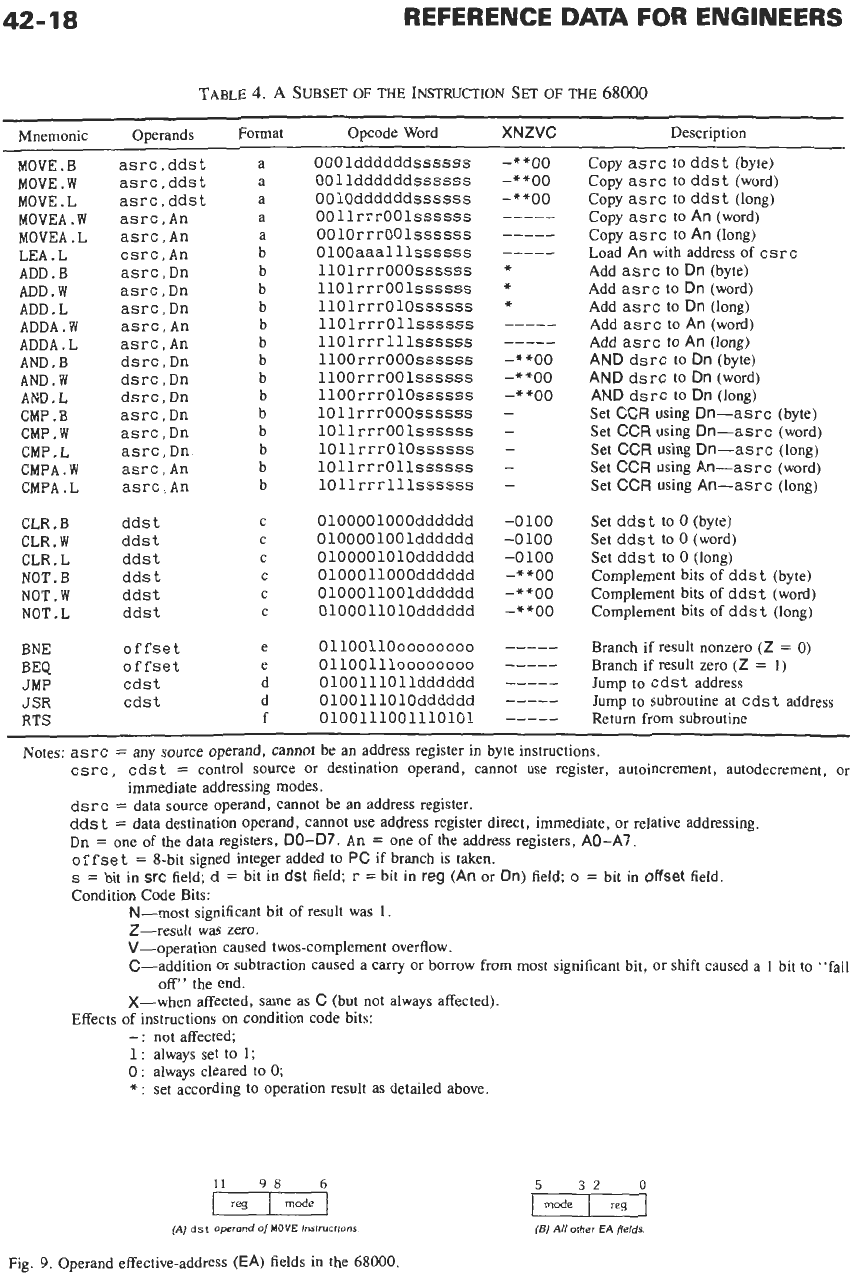
Table
4
lists a subset of the 68000 instruction set; the
full 68000 has many more instructions. There are
several different formats for the opcode word, as was
shown in Fig. 8. Associated with each opcode word is
an alphabetic
mnemonic
that we can use to name and
recognize the operation performed by that instruction.
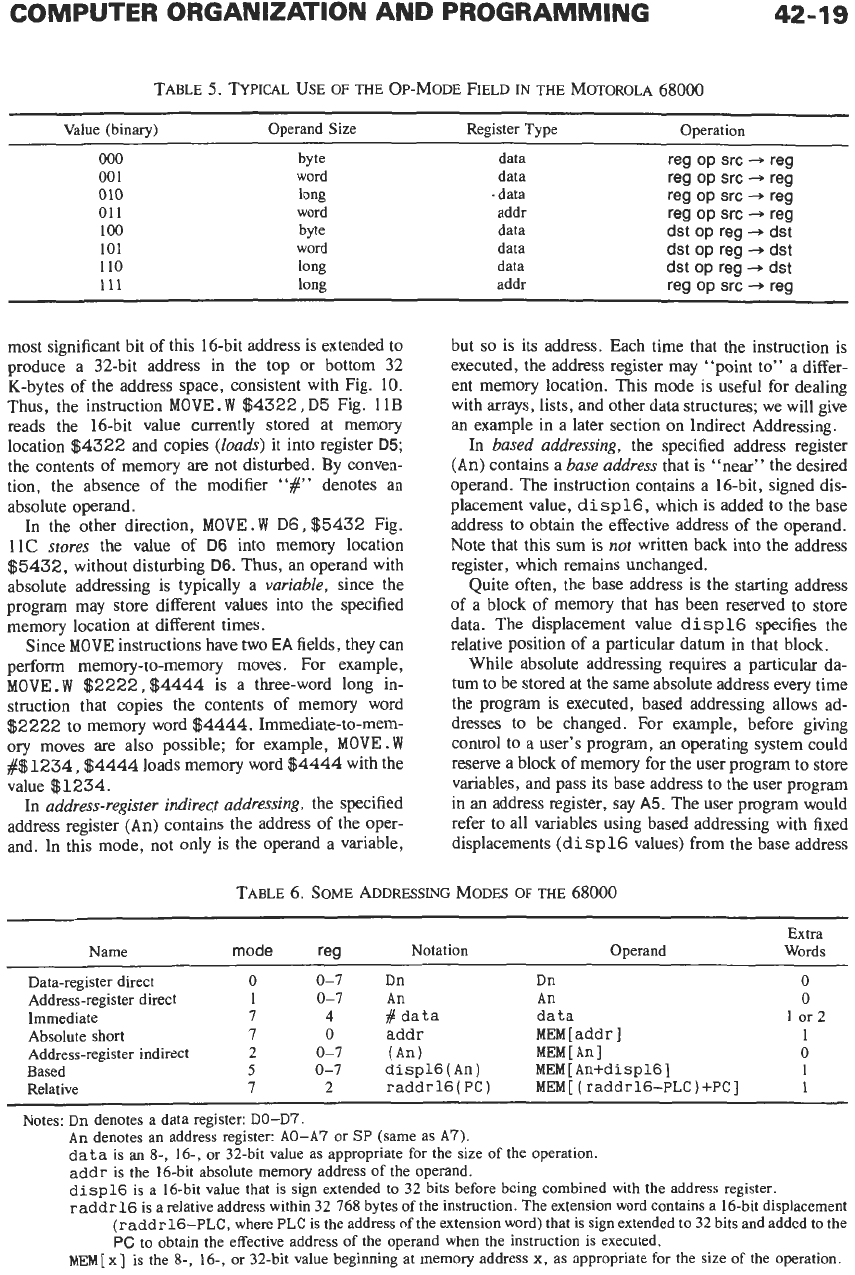
Note that our subset of the 68000 uses only four of
the eight possible binary values in the 3-bit
op-mode
field; the complete 68000 uses them all, as listed in
Table
5.
In both the subset and the complete 68000,
there
are
still more variations in each instruction
according to the addressing modes specified for the
source
(src)
and destination
(dst)
fields,
as
discussed in
the next subsection. After that, we will describe the
actual operations that are performed by each instruc-
tion.
opcode condition displacement
I
Addressing Modes
opcode
In the 68000, an operand is specified by a 6-bit
source or destination
EA
field in the instruction, con-
sisting of a 3-bit addressing mode designator and a 3-bit
register number, as shown in Fig.
9.
In conjunction with
the
reg
field, the eight
mode
combinations
are
used as
follows:
0
1
2-6
7
reg
specifies a data register
(DO-D7)
that
contains the operand.
reg
specifies an address register
(AO-A7)
that contains the operand.
reg
specifies an address register that is used,
possibly in combination with other values, to
determine the effective address of an
operand in memory.
reg
does not specify a register at all; instead,
the three
reg
bits specify one of five
addressing modes that do not use a general
register; three combinations are left over for
future expansion.
A full treatment of 68000 addressing modes is beyond
the scope of this chapter, but we shall discuss here the
seven most important ones, which are summarized in
Table 6.
In
register-direct addressing,
the operand is contained
in one of the data registers
DO-D7
or
in one of the
address registers
AO-A7.
As suggested by the dash lines
in Fig.
7,
word operations on the data registers use the
low-order 16 bits, while byte operations use only the
8
low-order bits; the high-order bits in both cases are
unaffected.
Word operations on the address registers also use the
low-order 16 bits, but a write operation into an address
register extends the most significant bit of the low-order
word into the high-order word. This is consistent with
the
short-addressing model
of the 68000 memory shown
in Fig. 10, in which a 16-bit number can specify a
memory address in the highest or lowest 32-kbyte
portion of a 4-gigabyte (32-bit) address space.
Byte operations are not allowed on address registers,
since an “address” should normally be at least a 16-bit
quantity. The complete 68000 instruction set provides
long-word operations on address registers, in order to
handle addresses up to 32 bits long.
Register-direct addressing is not allowed with the
68000
JMP and
JSR
instructions, since it does not
make sense to jump to a register.
In
immediate addressing,
a 1-, 2-, or 4-byte operand
is contained in the second and possibly third word of the
instruction, as appropriate for the size of the operation;
with 1-byte operands, the high-order byte of the imme-
diate word is unused.
Thus,
to place the value 1234,, in
register
D5,
we could use the instruction, M0VE.W
#$1234,
D5.
By convention, the notation
“#”
de-
notes an immediate operand, while the dollar sign
($)
denotes a hexadecimal value. The machine language
instruction occupies two words as shown in Fig. 11A.
With immediate addressing, the operand is
constant
value. Immediate mode cannot be used for a “destina-
tion” operand, since it would require the instruction to
modify itself. Thus, M0VE.W
D5,#$1234
is not
allowed.
In
absolute short addressing,
the instruction contains
a 16-bit absolute memory address for the operand. The
42-18
TABLE
4.
A
SUBSET
OF
THE
INSTRUCTION SET
OF
THE
68000
Mnemonic Operands Format Opcode Word XNZVC Description
MOVE.
B
MOVE.
W
MOVE. L
MOVEA
.
W
MOVEA
.
L
LEA. L
ADD.
B
ADD.W
ADD,
L
ADDA
.
W
ADDA
.
L
AND.
B
AND.
W
AND.
L
CMP
.
B
CMP
,
W
CMP
,
L
CMPA
.
W
CMPA
.
L
CLR
,
B
CLR
.
W
CLR.L
NOT.
B
NOT,
W
NOT.
L
BNE
BEQ
JMP
JSR
RTS
asrc, ddst
a
asrc, ddst
a
asrc, ddst
a
asrc
,An a
asrc ,An
a
csrc,An
b
asrc,
Dn b
asrc,
Dn
b
asrc,
Dn b
asrc,
An b
asrc,
An b
dsrc,
Dn b
dsrc,
Dn b
dsrc,
Dn b
asrc
,
Dn b
asrc,
Dn
b
asrc,Dn
b
asrc
I
An b
asrc,
An b
ddst
C
ddst
C
ddst
C
dds t
C
ddst
C
ddst
C
offset
e
offset
e
cdst
d
cdst
d
f
OOOlddddddssssss
OOllddddddssssss
OOlOddddddssssss
OOllrrrOOlssssss
00
1OrrrOOlssssss
OlOOaaalllssssss
11OlrrrOOOssssss
1lOlrrrOOlssssss
1lOlrrrOlOssssss
1lOlrrrOllssssss
1lOlrrrlllssssss
1lOOrrrOOOssssss
1lOOrrrOOlssssss
llOOrrrOlOssssss
lOllrrrOOOssssss
1OllrrrOOlssssss
1OllrrrOlOssssss
1OllrrrOllssssss
1Ollrrrlllssssss
OlOOOOlOOOdddddd
OlOOOOlOOldddddd
OlOOOOlOlOdddddd
OlOOOllOOOdddddd
OlOOOllOOldddddd
OlOOOllOlOdddddd
0110011000000000
0110011100000000
0
100 1110 lldddddd
OlOOlllOlOdddddd
0100111001110101
-----
-**oo
-**oo
-**oo
-
-
-
-
-
-0100
-0100
-0100
-**oo
-**oo
-**oo
Copy
asrc
to
ddst
(byte)
Copy
asrc
to
ddst
(word)
Copy
asrc
to
ddst
(long)
Copy
asrc
to
An
(word)
Copy
asrc
to
An
(long)
Load
An
with address of
csrc
Add
asrc
to
Dn
(byte)
Add
asrc
to
Dn
(word)
Add
asrc
to
Dn
(long)
Add
asrc
to
An
(word)
Add
asrc
to
An
(long)
AND
dsrc
to
Dn
(byte)
AND
dsrc
to
Dn
(word)
AND
dsrc
to
Dn
(long)
Set CCR using
Dn-asrc
(byte)
Set CCR using
Dn-asrc
(word)
Set CCR using
Dn-asrc
(long)
Set CCR using
An-asrc
(word)
Set CCR using
An-asrc
(long)
Set
ddst
to
0
(byte)
Set
ddst
to
0
(word)
Set
ddst
to
0
(long)
Complement bits of
ddst
(byte)
Complement bits of
ddst
(word)
Complement bits of
ddst
(long)
Branch if result nonzero
(2
=
0)
Branch if result zero
(Z
=
1)
Jump to
cdst
address
Jump to subroutine at
cds
t
address
Return from subroutine
Notes:
asrc
=
any source operand, cannot be an address register in byte instructions.
csrc
,
cdst
=
control source or destination operand, cannot
use
register, autoincrement, autodecrement,
or
immediate addressing modes.
dsrc
=
data source operand, cannot be an address register.
dds t
=
data destination operand, cannot use address register direct, immediate, or relative addressing,
Dn
=
one of the data registers,
DO-D7.
An
=
one of the address registers,
AO-A7.
offset
=
8-bit signed integer added to PC if branch is taken.
s
=
bit in
src
field;
d
=
bit in
dst
field;
r
=
bit in
reg
(An
or
Dn)
field;
o
=
bit in
offset
field.
Condition Code Bits:
N-most significant bit of result was
1.
2-result was zero.
V-operation caused twos-complement overflow.
C-addition
or
subtraction caused a
carry
or
borrow from most significant bit,
or
shift caused a
1
bit to “fall
X-when affected,
same
as C (but not always affected).
-
:
not affected;
1
:
always set
to
1;
0
:
always cleared to
0;
*
:
set according to operation result as detailed above.
off’
the end.
Effects of instructions on condition code bits:
11
98
6
(71
(A)
dst
operond
of
MOVE
instructions
Fig.
9.
Operand effective-address
(EA)
fields in the 68000
5
32
0
pzq--Gq
(51
All other
EA
fidds.
COMPUTER ORGANIZATION AND PROGRAMMING
42-19
TABLE
5.
TYPICAL
USE
OF
THE
OP-MODE
FIELD
IN
THE
MOTOROLA
68000
~
Value (binary) Operand Size Register Type Operation
000
byte
data
reg
op
src
+
reg
00
1
word
data
reg
op
src
+
reg
010
long
.
data
reg
op
src
-j
reg
01 1 word
addr
reg
op
src
+
reg
100 byte
data
dst
op
reg
+
dst
101 word data
dst
op
reg
+
dst
110
long
data
dst
op reg
+
dst
111
long addr
reg
op
src
-+
reg
most significant bit of this 16-bit address is extended to
produce a 32-bit address in
the
top or bottom
32
K-bytes of the address space, consistent with Fig. 10.
Thus, the instruction
MOVE. W
$4322,
D5
Fig. 11B
reads the 16-bit value currently stored at memory
location
$4322
and copies
(Zoads)
it into register
D5;
the contents of memory are not disturbed. By conven-
tion, the absence of the modifier
“#”
denotes an
absolute operand.
In the other direction,
MOVE.
W
D6, $5432
Fig.
11C
stores
the value
of
D6
into memory location
$5432,
without disturbing
D6.
Thus, an operand with
absolute addressing is typically a
variable,
since the
program may store different values into the specified
memory location at different times.
Since
MOVE
instructions have two
EA
fields, they can
perform memory-to-memory moves. For example,
M0VE.W
$2222,$4444
is a three-word long in-
struction that copies the contents of memory word
$2222
to memory word
$4444.
Immediate-to-mem-
ory moves are also possible; for example,
M0VE.W
#$1234,
$4444
loads memory word
$4444
with the
value
$1234.
In
address-register indirect addressing,
the specified
address register
(An)
contains the address of the oper-
and. In this mode, not only is the operand a variable,
but
so
is its address. Each time that the instruction is
executed, the address register may “point to” a differ-
ent memory location. This mode is useful
for
dealing
with arrays, lists, and other data structures; we will give
an
example in a later section on Indirect Addressing.
In
based addressing,
the specified address register
(An)
contains a
base address
that
is
“near” the desired
operand. The instruction contains a 16-bit, signed dis-
placement value,
displ6,
which is added to the base
address to obtain the effective address of the operand.
Note that this sum
is
nor
written back into the address
register, which remains unchanged.
Quite often, the base address
is
the starting address
of a block of memory that has been reserved to store
data. The displacement value
displ6
specifies the
relative position of a particular datum in that block.
While absolute addressing requires a particular da-
tum to be stored at the same absolute address every time
the program is executed, based addressing allows ad-
dresses to be changed.
For
example, before giving
control to a user’s program, an operating system could
reserve a block of memory for the user program
to
store
variables, and pass its base address to the user program
in
an
address register, say
A5.
The user program would
refer to all variables using based addressing with fixed
displacements
(displ6
values) from the base address
TABLE
6.
SOME
ADDRESSING
MODES
OF
THE
68000
Name
mode reg
Notation
Extra
Operand Words
Data-register direct
0
0-7
Dn
Dn
0
Address-register direct
1
0-7
An
An
0
Absolute short
7
0
addr
MEM
[
addr
]
1
Address-register indirect
2 0-7
(An) MEM
[
An]
0
Based
5
0-7
displ6(
An)
MEM[An+displG]
1
Relative
7 2
raddrlG(PC) MEM[(raddrlG-PLC)+PC]
1
Immediate
7
4
#
data data
1
or 2
Notes:
Dn
denotes a data register:
DO-D7.
An
denotes an address register:
AO-A7
or
SP
(same as
A7).
data
is
an
8-,
16-, or 32-bit value as appropriate for the size of the operation.
addr
is the 16-bit absolute memory address
of
the operand.
displ6
is
a 16-hit value that is sign extended to 32 bits before being combined with the address register.
raddrl6
is a relative address within 32 768 bytes of the instruction. The extension word contains a 16-bit displacement
(raddr 16-PLC,
where
PLC
is the address of the extension word) that is sign extended to 32 bits and added to the
PC
to obtain the effective address of the operand when the instruction is executed.
MEM[x]
is
the 8-,
16-,
or
32-bit value beginning at memory address
x,
as appropriate for the size of the operation.
