Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

470
9.1. Математичесое обеспечение
автоматизированных систем
Мы рассмотрим математичесое обеспечение применительно
системам правления производством, во-первых, потом, что в
настоящее время этот ласс систем является наиболее разрабо-
танным, и, во-вторых, наиболее типичным.
В соответствии с ГОСТом, под математичесим обеспечением
понимается совопность математичесих моделей, методов и
ал оритмов для решения задач обработи информации с приме-
нением средств вычислительной технии.
Если математичесое обеспечение рассматривать с позиций
использемо о математичесо о аппарата, то е о можно разде-
лить на три части:
Задачи лоичесой обработи информации (типа сортирови,
слияния, объединения и т. п.). Эти задачи, а правило, реализо-
ваны в стандартном про раммном обеспечении.
Задачи прямоо счета, или, их еще называют, ртинные зада-
чи. Это вычисления по известным соотношениям смм, произве-
дений, смм произведений и т. д. Типичный пример — расчет за-
работной платы повременщиа: необходимо е о почасовю та-
рифню став множить на число отработанных им часов, затем
честь надбави, если они положены, затем произвести вычеты,
оторые положены все да; в ито е полчим величин заработной
платы, подлежащю выдаче.
Задачи оптимизации. Процесс оптимизации предпола ает вы-
бор тао о варианта решения, при отором дости ается эстре-
мальное (масимальное или минимальное) значение неоторой
фнции, харатеризющей ачество правления. Выбор этой
фнции осществляется постановщиом задачи в зависимости
от целей, стоящих перед системой правления.
Наиболее часто использются следющие основные эономи-
о-математичесие модели правления производством (ЭММ):
1) модели, оторые полчили название производственные фн-
ции. Это простейший вид моделей. Они представляют собой ал еб-
раичесие зависимости межд различными фаторами и поазате-
лями производства. Примеры фаторов производства: числен-
ность основных рабочих, численность аппарата правления,
размер и степень амортизации основных средств, виды и оличес-
тво обордования и т. п. Примеры поазателей производства: при-
быль, себестоимость, оличество выпсаемой продции и т. п.;
2) балансовые модели. Они представляют собой линейные за-
висимости межд различными производственными фаторами и
471
поазателями производства. Типичный пример — модель межот-
раслево о баланса, оторая бдет рассматриваться ниже;
3) модели объемноо планирования. Это, по сти, те же самые ба-
лансовые модели, но с азанием неоторых ритериев оцени;
4) модели алендарноо планирования, или, а их еще называ-
ют, модели расписания. Они порядочивают по времени выпол-
нение тех или иных работ или событий. Проще оворя, это раз-
работа расписания неоторой деятельности;
5) потоовые модели. Они оперирют с потоами продции,
финансов, энер ии, сл одно о предприятия др им и т. п. Ча-
ще все о эти модели отображаются с помощью рафов;
6) модели правления запасами. С одной стороны, наопление
запасов ведет излишним издержам, связанным с их хранени-
ем, запасы мо т терять ачество, морально старевать и т. п. Все
это приводит финансовым потерям предприятия. С др ой сто-
роны, отстствие запасов и вызванные этим слчайные останов-
и производства вынждают предприятие-поставщи платить
штрафы своим потребителям за недопостав. Уазанные модели
оптимизирют эт ситацию;
7) модели распределения, оторые осществляют поис реше-
ния в словиях взаимозаменяемости обордования, техноло ий,
процессов и т. п.;
8) модели массовоо обслживания. В отличие от всех предыд-
щих моделей, они читывают слчайный харатер различных
фаторов, воздействющих на производство. Например, момен-
ты выхода обордования из строя слчайны во времени, продол-
жительность ремонта таже величина слчайная. Если ремонтни-
ов очень мно о, то они бдт простаивать, и предприятие несет
быто; если их очень мало, то бдет простаивать обордование,
и предприятие снова понесет быти. Модели массово о обсл-
живания позволяют оптимизировать эти ситации;
9) имитационные модели. Это самый ниверсальный вид моде-
лей, посоль это есть не что иное, а эсперимент, проводи-
мый на ЭВМ, и, стало быть, с помощью имитации можно решать
любой из перечисленных выше лассов задач.
Модели типа «производственные фнции». Ка отмечалось,
это самый простейший вид моделей, они предназначены для вы-
работи общей эономичесой политии.
Пример 1. Определение размера партии выпсаемых деталей.
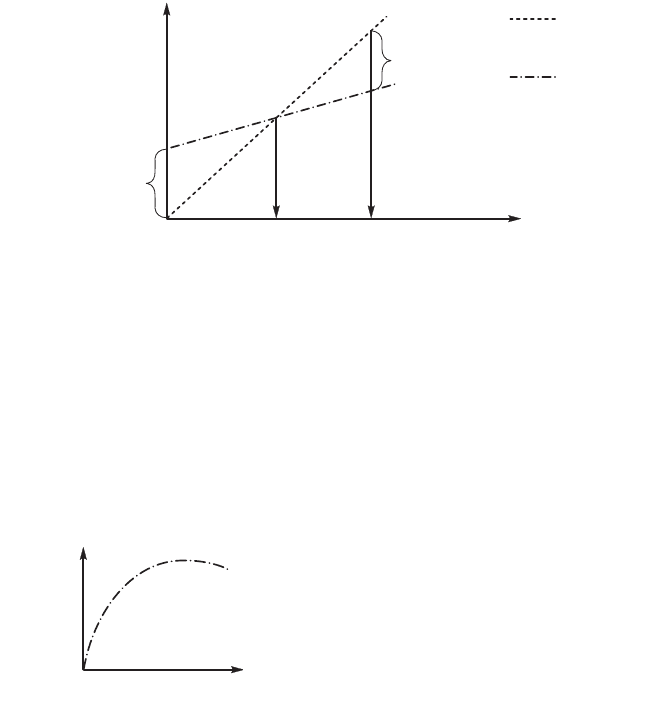
Псть цена партии деталей прямо пропорциональна оличес-
тв шт деталей в партии, а затраты на выпс таже прямо про-
порциональны оличеств деталей в партии и требют неоторых
первоначальных апиталовложений (рис 9.2).
472
Из рис. 9.2 следет, что, тольо начиная с неоторо о
оличества деталей N
0,
имеет смысл налаживать производство.
Если задаться желаемой величиной прибыли, то можно
определить, не менее ао о числа N должна содержать партия
деталей. В этом примере фатор производства — оличество
деталей, поазатель производства — прибыль.
Пример 2. Модель реализации про-
дции.
Из рис. 9.3 следет, что сначала
прибыль растет, а затем, по мере на-
сыщения рына данной продцией,
начинает падать.
Аналитичеси производственные
фнции записываются в виде:
y = f(x),
здесь y — поазатель производства, x —
фатор производства.
Приращение поазателя:
∆y = f ′(x) · ∆x.
Поис правляющих воздействий в таих моделях чрезвычай-
но прост:
—если f ′(x) > 0, то рост фатора x целесообразно стимлиро-
вать;
—если f ′(x) < 0, то целесообразно меньшать значение x;
—если f ′(x) = 0, то ситацию можно сохранить.
N
0
N
Ïåðâîíà÷àëüíûå
âëîæåíèÿ
Êîëè÷åñòâî
øòóê äåòàëåé
Öåíà
ïàðòèè
Çàòðàòû
íà âûïóñ
ê
Ïðèáûëü
Äåíüãè
Рис. 9.2. Определение размера партии деталей
Êîëè÷åñòâî
øòóê äåòàëåé
Ï
ðèáûëü
Рис.9.3. Модель реализа-
ции продции
473
На пратие очень часто производственные фнции являют-
ся фнциями несольих ар ментов (несольих производс-
твенных фаторов), т. е.
y = f (x
1
, x
2
, ..., x
n
).
В этом слчае аждая частная производная поазывает зави-
симость y от соответствюще о ар мента:
= , i =
и полное приращение производственно о поазателя y:
∆y = ∆x.
Сществют различные способы определения вида фнции f.
Можно, например, использя эмпиричесие данные, методами ре -
рессионно о анализа найти вид фнции f(x) или, например, задав-
шись из аих-либо соображений видом фнции f, опять же, ис-
пользя статисти, найти все параметры выбранной фнции.
Балансовые модели. В них использются свойства аддитив-
ности, линейности и взаимной независимости различных фато-
ров и поазателей производства. В самом общем слчае это мож-
но записать в виде следюще о баланса:
F = .
Читается эта запись та: влияние сммы равно смме влия-
ний. Здесь Ф
i
— это i-тый фатор производственно о процесса,
F — это влияние фаторов.
Балансовые модели оличественно связывают потои реср-
сов и продции, производственные мощности предприятия и
за рз обордования и т.п.
Типичный пример: модель межотраслево о баланса. Эта мо-
дель задается системой линейных равнений вида:
x
i
° = y
i
, i, j = .
В этом i-том равнении:
x
i
— это оличество неоторой продции, производимой
i-той отраслью;
dy
dx
i
-------
f
i
′
1 n,
f
i
′
i 1=
n
∑
⎝
⎛
Ф
i
i
∑
⎠
⎞
F Ф
i
()
i
∑
a
ij
x
j
j
1=
n
∑
1 n,

472
Из рис. 9.2 следет, что, тольо начиная с неоторо о
оличества деталей N
0,
имеет смысл налаживать производство.
Если задаться желаемой величиной прибыли, то можно
определить, не менее ао о числа N должна содержать партия
деталей. В этом примере фатор производства — оличество
деталей, поазатель производства — прибыль.
Пример 2. Модель реализации про-
дции.
Из рис. 9.3 следет, что сначала
прибыль растет, а затем, по мере на-
сыщения рына данной продцией,
начинает падать.
Аналитичеси производственные
фнции записываются в виде:
y = f(x),
здесь y — поазатель производства, x —
фатор производства.
Приращение поазателя:
∆y = f ′(x) · ∆x.
Поис правляющих воздействий в таих моделях чрезвычай-
но прост:
—если f ′(x) > 0, то рост фатора x целесообразно стимлиро-
вать;
—если f ′(x) < 0, то целесообразно меньшать значение x;
—если f ′(x) = 0, то ситацию можно сохранить.
N
0
N
Ïåðâîíà÷àëüíûå
âëîæåíèÿ
Êîëè÷åñòâî
øòóê äåòàëåé
Öåíà
ïàðòèè
Çàòðàòû
íà âûïóñ
ê
Ïðèáûëü
Äåíüãè
Рис. 9.2. Определение размера партии деталей
Êîëè÷åñòâî
øòóê äåòàëåé
Ï
ðèáûëü
Рис.9.3. Модель реализа-
ции продции
473
На пратие очень часто производственные фнции являют-
ся фнциями несольих ар ментов (несольих производс-
твенных фаторов), т. е.
y = f (x
1
, x
2
, ..., x
n
).
В этом слчае аждая частная производная поазывает зави-
симость y от соответствюще о ар мента:
= , i =
и полное приращение производственно о поазателя y:
∆y = ∆x.
Сществют различные способы определения вида фнции f.
Можно, например, использя эмпиричесие данные, методами ре -
рессионно о анализа найти вид фнции f(x) или, например, задав-
шись из аих-либо соображений видом фнции f, опять же, ис-
пользя статисти, найти все параметры выбранной фнции.
Балансовые модели. В них использются свойства аддитив-
ности, линейности и взаимной независимости различных фато-
ров и поазателей производства. В самом общем слчае это мож-
но записать в виде следюще о баланса:
F = .
Читается эта запись та: влияние сммы равно смме влия-
ний. Здесь Ф
i
— это i-тый фатор производственно о процесса,
F — это влияние фаторов.
Балансовые модели оличественно связывают потои реср-
сов и продции, производственные мощности предприятия и
за рз обордования и т.п.
Типичный пример: модель межотраслево о баланса. Эта мо-
дель задается системой линейных равнений вида:
x
i
° = y
i
, i, j = .
В этом i-том равнении:
x
i
— это оличество неоторой продции, производимой
i-той отраслью;
dy
dx
i
-------
f
i
′
1 n,
f
i
′
i 1=
n
∑
⎝
⎛
Ф
i
i
∑
⎠
⎞
F Ф
i
()
i
∑
a
ij
x
j
j
1=
n
∑
1 n,
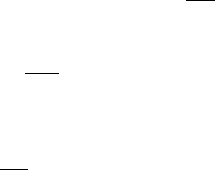
474
y
i
— это оличество продции, идщей на внтриотрасле-
вое потребление, т. е. остающейся в этой отрасли;
a
ij
— это оличество продции i-той отрасли, идщей на
производство единицы продции в j-тю отрасль;
a
ij
x
j
— это полное оличество продции, постпающей из
i-той в j-тю отрасль.
Анало ичной моделью можно описать связи межд предпри-
ятиями по продции, сл и одно о производственно о объета,
оазываемые др ом производственном объет, и т. п. задачи.
Балансовые модели дают точные про нозы тольо для стано-
вивше ося производственно о процесса. Их построение связано
с необходимостью определения специальных оэффициентов за-
трат или нормативов a
ij
. Если эти оэффициенты меняются во
времени, то необходимо меть про нозировать их бдщие зна-
чения.
Модели объемноо планирования. Это типичный пример зада-
чи принятия решений с детерминированными параметрами.
Псть имеется несольо производственных объетов, этими
объетами мо т быть части цеха, цеха на предприятии, пред-
приятия в отрасли и т.д. Обозначим эти производственные объ-
еты через A
1
, A
2
, ..., A
n
, A
r
— тещий объет, r = .
Псть все эти производственные объеты способны выпс-
ать неоторые изделия, оторые обозначим через B
1
, B
2
, ..., B
m
,
неоторое тещее изделие B
i
, i = .
Для выпса этих изделий необходимо иметь k ресрсов (ра-
бочие различной валифиации и профессий, инженеры, стани
и т. п.). Обозначим эти производственные ресрсы через C
1
, C
2
,
..., C
k
, тещий ресрс — C
j
, j = .
На аждый вид выпсаемой продции имеется диретив-
ный план, т. е. то оличество изделий данно о вида, не менее о-
торо о все производственные объеты должны выпстить все
вместе. Обозначим диретивный план выпса изделия B
i
через b
i
Известны нормативы: норматив использования ресрса C
j
,
оторый необходим для выпса одной шти изделия B
i
, обоз-
начим через с
ij
.
Время использования аждо о из ресрсов C
j
есть величина
о раниченная (не более 24 часов в сти), роме то о, для аждо-
о из производственных объетов эта величина различная (т. . на
одном предприятии, например, может быть трехсменная работа,
на др ом — двхсменная и т. п.). Обозначим допстимое время ис-
пользования ресрса C
j
на производственном объете A
r
, через a
rj
.
Известна таже прибыль аждо о производственно о объета
от выпса одно о изделия аждо о вида. Обозначим прибыль,
1 n,
1 m,
1 k,
475
оторю полчает объет A
r
, выпсая одн шт изделий типа
B
i,
через P
ri
.
Требется та распределить план выпса всех изделий меж-
д всеми объетами, чтобы сммарная прибыль была бы маси-
мальной.
Это словесное описание задачи (проблемы). Теперь разрабо-
таем ее математичесю модель.
Обозначим через X
ri
план выпса изделий типа B
i
, i = ,
оторый мы порчим предприятию или производственном объ-
ет A
r
, r = . Следет отметить, что аждый из производс-
твенных объетов, выпсая одн шт изделий типа B
i
, полча-
ет различню прибыль в зависимости от техноло ии, ор аниза-
ции трда и т.п.
Рассмотрим объет A
r
: выпсая одн шт изделий типа B
i,
это предприятие полчает прибыль P
ri
, но по план, оторый мы
ищем, он должен выпсать X
ri
шт, значит, прибыль это о объ-
ета от выпса данно о изделия составит P
ri
X
ri
. Анало ичные
рассждения можно провести и для любо о из перечисленных из-
делий, следовательно, сммарная прибыль объета бдет слады-
ваться от выпса всех изделий, значит, азанню величин надо
просммировать по всем изделиям. В резльтате прибыль объета
A
r
бдет равна:
.
Но нас интересет сммарная прибыль всех объетов, поэто-
м азанню величин необходимо просммировать по всем
объетам. Сммарная прибыль составит:
= F .(9.1)
Ита, задача залючается в том, чтобы найти таие X
ri
, ото-
рые бы обеспечивали масимм выражения (9.1), но при этом на
все X
ri
наладываются следющие о раничения: исомые плана
X
ri
не мо т быть отрицательными
X
ri
l 0, r = , i = , (9.2)
второй вид о раничений вытеает из необходимости выполнения
диретивных планов. Одно предприятие выпсает X
ri
шт изде-
лий, то да полный объем выпса этих изделий полчится в ре-
1 m,
1 n,
P
ri
X
ri
i 1=
m
∑
P
ri
X
ri
i 1=
m
∑
r 1=
n
∑
1 n, 1 m,

474
y
i
— это оличество продции, идщей на внтриотрасле-
вое потребление, т. е. остающейся в этой отрасли;
a
ij
— это оличество продции i-той отрасли, идщей на
производство единицы продции в j-тю отрасль;
a
ij
x
j
— это полное оличество продции, постпающей из
i-той в j-тю отрасль.
Анало ичной моделью можно описать связи межд предпри-
ятиями по продции, сл и одно о производственно о объета,
оазываемые др ом производственном объет, и т. п. задачи.
Балансовые модели дают точные про нозы тольо для стано-
вивше ося производственно о процесса. Их построение связано
с необходимостью определения специальных оэффициентов за-
трат или нормативов a
ij
. Если эти оэффициенты меняются во
времени, то необходимо меть про нозировать их бдщие зна-
чения.
Модели объемноо планирования. Это типичный пример зада-
чи принятия решений с детерминированными параметрами.
Псть имеется несольо производственных объетов, этими
объетами мо т быть части цеха, цеха на предприятии, пред-
приятия в отрасли и т.д. Обозначим эти производственные объ-
еты через A
1
, A
2
, ..., A
n
, A
r
— тещий объет, r = .
Псть все эти производственные объеты способны выпс-
ать неоторые изделия, оторые обозначим через B
1
, B
2
, ..., B
m
,
неоторое тещее изделие B
i
, i = .
Для выпса этих изделий необходимо иметь k ресрсов (ра-
бочие различной валифиации и профессий, инженеры, стани
и т. п.). Обозначим эти производственные ресрсы через C
1
, C
2
,
..., C
k
, тещий ресрс — C
j
, j = .
На аждый вид выпсаемой продции имеется диретив-
ный план, т. е. то оличество изделий данно о вида, не менее о-
торо о все производственные объеты должны выпстить все
вместе. Обозначим диретивный план выпса изделия B
i
через b
i
Известны нормативы: норматив использования ресрса C
j
,
оторый необходим для выпса одной шти изделия B
i
, обоз-
начим через с
ij
.
Время использования аждо о из ресрсов C
j
есть величина
о раниченная (не более 24 часов в сти), роме то о, для аждо-
о из производственных объетов эта величина различная (т. . на
одном предприятии, например, может быть трехсменная работа,
на др ом — двхсменная и т. п.). Обозначим допстимое время ис-
пользования ресрса C
j
на производственном объете A
r
, через a
rj
.
Известна таже прибыль аждо о производственно о объета
от выпса одно о изделия аждо о вида. Обозначим прибыль,
1 n,
1 m,
1 k,
475
оторю полчает объет A
r
, выпсая одн шт изделий типа
B
i,
через P
ri
.
Требется та распределить план выпса всех изделий меж-
д всеми объетами, чтобы сммарная прибыль была бы маси-
мальной.
Это словесное описание задачи (проблемы). Теперь разрабо-
таем ее математичесю модель.
Обозначим через X
ri
план выпса изделий типа B
i
, i = ,
оторый мы порчим предприятию или производственном объ-
ет A
r
, r = . Следет отметить, что аждый из производс-
твенных объетов, выпсая одн шт изделий типа B
i
, полча-
ет различню прибыль в зависимости от техноло ии, ор аниза-
ции трда и т.п.
Рассмотрим объет A
r
: выпсая одн шт изделий типа B
i,
это предприятие полчает прибыль P
ri
, но по план, оторый мы
ищем, он должен выпсать X
ri
шт, значит, прибыль это о объ-
ета от выпса данно о изделия составит P
ri
X
ri
. Анало ичные
рассждения можно провести и для любо о из перечисленных из-
делий, следовательно, сммарная прибыль объета бдет слады-
ваться от выпса всех изделий, значит, азанню величин надо
просммировать по всем изделиям. В резльтате прибыль объета
A
r
бдет равна:
.
Но нас интересет сммарная прибыль всех объетов, поэто-
м азанню величин необходимо просммировать по всем
объетам. Сммарная прибыль составит:
= F .(9.1)
Ита, задача залючается в том, чтобы найти таие X
ri
, ото-
рые бы обеспечивали масимм выражения (9.1), но при этом на
все X
ri
наладываются следющие о раничения: исомые плана
X
ri
не мо т быть отрицательными
X
ri
l 0, r = , i = , (9.2)
второй вид о раничений вытеает из необходимости выполнения
диретивных планов. Одно предприятие выпсает X
ri
шт изде-
лий, то да полный объем выпса этих изделий полчится в ре-
1 m,
1 n,
P
ri
X
ri
i 1=
m
∑
P
ri
X
ri
i 1=
m
∑
r 1=
n
∑
1 n, 1 m,

476
зльтате сммирования X
ri
по всем предприятиям. И эта величина
не может быть меньше диретивно о плана b
i
т. е.
m b
i
, i = , (9.3)
следющая рппа о раничений вытеает из о раниченности ре-
срсов. Выпсая 1шт. изделий вида B
i
, мы занимаем ресрс C
j
в
течении времени c
ij
(например, 1/2 часа из отавливается он-
ретная деталь на онретном стане). Но выпсать мы бдем X
ri
шт изделий. Стало быть с
ij
X
ri
— время занятости данно о реср-
са выпсом деталей тольо это о вида. Но этот же ресрс может
быть занят выпсом и др их изделий. То да — полное
время занятости ресрса C
j
. Но время использования аждо о из
ресрсов есть величина о раниченная, поэтом
m a
rj
, r = , j = . (9.4)
И, оончательно, необходимо найти таие планы выпса
всех изделий на всех производственных объетах X
ri
, оторые бы
обращали в масимм выражение (9.1) при соблюдении систем
о раничений (9.2—9.4).
Если решать эт задач в масштабах отрасли, то приблизи-
тельными параметрами задачи бдт: число предприятий n = 20,
число видов продции m = 50, число видов ресрсов k = 10.
В резльтате число о раничений составит 1250.
Рассмотрим числовой пример модели объемно о планирования.
Псть, для простоты, мы имеем все о один производственный
объет (сажем, цех). Стало быть, в выше азанных обозначени-
ях, n = 1, A
1
— производственный объет.
Псть таже этот объет способен выпсать тольо два вида
изделий. То да, в этих же обозначениях, m = 2, изделия — B
1
и B
2
.
Псть таже для выпса этих двх изделий требются все о
два вида производственных ресрсов. В выше азанных обозна-
чениях, k = 2, C
1
и C
2
— производственные ресрсы.
Известны нормативы: для выпса одной шти изделий вида B
1
ресрс C
1
необходимо использовать один час, а ресрс C
2
— два часа.
Анало ично, для выпса одной шти изделий вида B
2
ресрс C
1
требется использовать два часа, а ресрс C
2
— один час (рис. 9.4).
X
ri
i 1=
m
∑
1 m,
c
ij
X
ri
i 1=
m
∑
c
ij
X
ri
i 1=
m
∑
1 n, 1 k,
477
Масимально возможное время использования ресрса C
1
—
8 часов в сти, а ресрса C
2
— 10 часов.
Известна прибыль, оторю полчает производственный объет
от выпса этих изделий. Псть, выпсая 1 шт изделий B
1
, про-
изводственный объет полчает прибыль 5 тыс. рб., а если он же
выпсает 1 шт изделий B
2
, то он полчает прибыль 3 тыс.рб.
Для простоты бдем считать, что диретивные планы на вы-
пс этих изделий отстствют.
Требется составить план выпса этих изделий, оторый
обеспечивал бы производственном объет масимальню
прибыль.
Мы разработали словесное описание задачи (словесное опи-
сание серьезной задачи может составлять несольо томов).
Разработаем теперь математичесю модель, для это о обоз-
начим план выпса, или оличество изделий, обеспечивающих
масимальню прибыль, для изделия B
1
через X
1
; для изделия
B
2
— X
2
; X
1
и X
2
— исомые правляющие воздействия, оторые
необходимо отысать, это та называемый правляемый пара-
метр задачи.
Сначала распишем выражение для прибыли. Выпсая 1 шт. B
1
,
производственный объет полчает 5 тыс.рб. прибыли, а шт
этих бдет X
1
; 5 X
1
— прибыль, полчаемая им от выпса изделий
B
1
, плюс этом 3 тыс. рб. от выпса 1 шт. B
2
, а шт этих X
2
;
3X
2
— прибыль от выпса изделий B
2
, а смма (5X
1
+ 3X
2
) и бдет
составлять сммарню прибыль предприятия.
5X
1
+ 3X
2
= F,тебетсяF → max. (9.5)
Выражение (9.5) есть ритерий оптимальности принимаемо о
решения, е о еще называют целевой фнцией. Если бы не было
о раничений, то, выпсая бесонечно мно о изделий одно о ви-
да, можно было бы полчать бесонечно большю прибыль, но
имеются о раничения, оторые определяют область допстимых
значений правляемых параметров задачи. Рассмотрим эти о ра-
ничения.
1 шт.
B
1
С
1
= 1
С
2
= 2
1 шт.
B
2
С
2
= 1
С
1
= 2
Рис. 9.4. Использование ресрсов для выпса 1 шт. B
1
и 1 шт. B
2

476
зльтате сммирования X
ri
по всем предприятиям. И эта величина
не может быть меньше диретивно о плана b
i
т. е.
m b
i
, i = , (9.3)
следющая рппа о раничений вытеает из о раниченности ре-
срсов. Выпсая 1шт. изделий вида B
i
, мы занимаем ресрс C
j
в
течении времени c
ij
(например, 1/2 часа из отавливается он-
ретная деталь на онретном стане). Но выпсать мы бдем X
ri
шт изделий. Стало быть с
ij
X
ri
— время занятости данно о реср-
са выпсом деталей тольо это о вида. Но этот же ресрс может
быть занят выпсом и др их изделий. То да — полное
время занятости ресрса C
j
. Но время использования аждо о из
ресрсов есть величина о раниченная, поэтом
m a
rj
, r = , j = . (9.4)
И, оончательно, необходимо найти таие планы выпса
всех изделий на всех производственных объетах X
ri
, оторые бы
обращали в масимм выражение (9.1) при соблюдении систем
о раничений (9.2—9.4).
Если решать эт задач в масштабах отрасли, то приблизи-
тельными параметрами задачи бдт: число предприятий n = 20,
число видов продции m = 50, число видов ресрсов k = 10.
В резльтате число о раничений составит 1250.
Рассмотрим числовой пример модели объемно о планирования.
Псть, для простоты, мы имеем все о один производственный
объет (сажем, цех). Стало быть, в выше азанных обозначени-
ях, n = 1, A
1
— производственный объет.
Псть таже этот объет способен выпсать тольо два вида
изделий. То да, в этих же обозначениях, m = 2, изделия — B
1
и B
2
.
Псть таже для выпса этих двх изделий требются все о
два вида производственных ресрсов. В выше азанных обозна-
чениях, k = 2, C
1
и C
2
— производственные ресрсы.
Известны нормативы: для выпса одной шти изделий вида B
1
ресрс C
1
необходимо использовать один час, а ресрс C
2
— два часа.
Анало ично, для выпса одной шти изделий вида B
2
ресрс C
1
требется использовать два часа, а ресрс C
2
— один час (рис. 9.4).
X
ri
i 1=
m
∑
1 m,
c
ij
X
ri
i 1=
m
∑
c
ij
X
ri
i 1=
m
∑
1 n, 1 k,
477
Масимально возможное время использования ресрса C
1
—
8 часов в сти, а ресрса C
2
— 10 часов.
Известна прибыль, оторю полчает производственный объет
от выпса этих изделий. Псть, выпсая 1 шт изделий B
1
, про-
изводственный объет полчает прибыль 5 тыс. рб., а если он же
выпсает 1 шт изделий B
2
, то он полчает прибыль 3 тыс.рб.
Для простоты бдем считать, что диретивные планы на вы-
пс этих изделий отстствют.
Требется составить план выпса этих изделий, оторый
обеспечивал бы производственном объет масимальню
прибыль.
Мы разработали словесное описание задачи (словесное опи-
сание серьезной задачи может составлять несольо томов).
Разработаем теперь математичесю модель, для это о обоз-
начим план выпса, или оличество изделий, обеспечивающих
масимальню прибыль, для изделия B
1
через X
1
; для изделия
B
2
— X
2
; X
1
и X
2
— исомые правляющие воздействия, оторые
необходимо отысать, это та называемый правляемый пара-
метр задачи.
Сначала распишем выражение для прибыли. Выпсая 1 шт. B
1
,
производственный объет полчает 5 тыс.рб. прибыли, а шт
этих бдет X
1
; 5 X
1
— прибыль, полчаемая им от выпса изделий
B
1
, плюс этом 3 тыс. рб. от выпса 1 шт. B
2
, а шт этих X
2
;
3X
2
— прибыль от выпса изделий B
2
, а смма (5X
1
+ 3X
2
) и бдет
составлять сммарню прибыль предприятия.
5X
1
+ 3X
2
= F,тебетсяF → max. (9.5)
Выражение (9.5) есть ритерий оптимальности принимаемо о
решения, е о еще называют целевой фнцией. Если бы не было
о раничений, то, выпсая бесонечно мно о изделий одно о ви-
да, можно было бы полчать бесонечно большю прибыль, но
имеются о раничения, оторые определяют область допстимых
значений правляемых параметров задачи. Рассмотрим эти о ра-
ничения.
1 шт.
B
1
С
1
= 1
С
2
= 2
1 шт.
B
2
С
2
= 1
С
1
= 2
Рис. 9.4. Использование ресрсов для выпса 1 шт. B
1
и 1 шт. B
2

478
Первое о раничение — исходные планы не мо т быть отри-
цательны, если мы порчим выпсать изделие B
1
, то X
1
> 0 если
не порчим, то X
1
= 0. Это справедливо и для X
2
т. е.
X
1
l 0, X
2
l 0. (9.6)
Опять же, для простоты, мы снимаем требования целочислен-
ности X
1
и X
2
.
Второе о раничение — о раничение по времени использова-
ния ресрсов. Рассмотрим ресрс C
1
— выпсая 1 шт. изделий B
1
,
ресрс C
1
необходимо использовать 1 час, а все о бдет выпсать-
ся X
1
шт, следовательно, для выпса всех изделий вида B
1
ре-
срс C
1
бдет занят 1 × X
1
часов, но ресрс C
1
занят таже и выпс-
ом B
2
. То да полное время занятости ресрса C
1
бдет X
1
+ 2X
2
, но,
по словию, масимально возможное время использования ре-
срса C
1
не может превышать 8 часов, значит,
X
1
+ 2X
2
m 8. (9.7)
Совершенно анало ично расписывается о раничение и по ис-
пользованию ресрса C
2
:
2X
1
+ X
2
m 10. (9.8)
Ита, требется найти таие значения X
1
и X
2
(таие планы,
таие правляющие воздействия), оторые бы, довлетворяя о -
раничениям (9.6—9.8) (оторые определяют область допстимых
значений правляющих воздействий), обращали бы в масимм
выражение (9.5) (ритерий эффетивности). И, оончательно,
5X
1
+ 3X
2
= F → max при .
Модели алендарноо планирования. Эти модели порядочи-
вают во времени выполнение аих-либо работ или событий.
Математичесим аппаратом моделей алендарно о планирова-
ния является теория расписаний. Рассмотрим типичный пример
моделей алендарно о планирования.
Псть имеется m деталей, подлежащих обработе; обработа
идет на n станах: i = , j = . Маршрт обработи, то есть
порядо прохождения аждой детали станов, всех деталей оди-
2X
1
+ X
2
m 10,
X
1
+ 2X
2
m 8,
X
1
l 0,
X
2
l 0
1 m,
1 n,
479
наов, но время обработи естественно различное. Требется
порядочить очередь деталей на входе, т.е. определить таю пос-
ледовательность запса деталей в производство, оторая мини-
мизировала бы сммарное время обработи всех деталей.
Эт задач можно проиллюстрировать рисном 9.5.
Уазанная задача решается при следющих о раничениях: для
аждой детали i ее обработа на стане j может начаться не ранее,
чем она заончится на стане (j-1). Если t
ij
— время начала обра-
боти i-той детали на j-том стане; — время оончания об-
работи i-той детали на j-том стане, то можно записать:
t
ij
l ,
на аждом стане одновременно может обрабатываться тольо
одна деталь.
Процесс обработи детали не прерывается до полно о е о за-
вершения
= t
ij
+ t
ij
.
В настоящее время азанная задача стро о решена тольо
для слчая двх станов. При n > 2 использются либо эвристи-
чесие приемы, не арантирющие отысания лобально о эс-
тремма, либо перебор всех возможных ситаций.
Пример. Псть n = 2. В этом слчае может быть использован ал-
оритм Джонсона. Обозначим для простоты t
i,1
через a
i
, t
i,2
через b
i
.
Первый ша алоритма. Среди чисел (a
1
, a
2
, …, a
m
, b
1
, b
2
, …, b
i
,
…, b
m
) ищется наименьшее число. Если этим числом оазывается
число a
i
, то пола ают i = i
1
, т. е. помещают i-тю деталь на первое
место в расписании. Если наименьшим числом оазалось число
b
i
, то пола ают i = i
m
, т. е. помещают i-тю деталь на последнее
место в расписании. Если а в 1-м, та и во 2-м слчае оазалось
несольо равных чисел, то берт любое из них, затем деталь i
вычеривается из расписания (т. е. вычериваются числа (a
i
, b
i
)).
k-тый ша алоритма (1<k<m): Среди оставшихся чисел, еще
не вычернтых на предыдщих ша ах, находим наименьшее
2 3
{i}
1
t
i1
t
i2
t
i3
n = 3, i = 1, m
Рис. 9.5. Модель алендарноо планирования
t
ij 1−()
t
ij 1−()
t
ij

478
Первое о раничение — исходные планы не мо т быть отри-
цательны, если мы порчим выпсать изделие B
1
, то X
1
> 0 если
не порчим, то X
1
= 0. Это справедливо и для X
2
т. е.
X
1
l 0, X
2
l 0. (9.6)
Опять же, для простоты, мы снимаем требования целочислен-
ности X
1
и X
2
.
Второе о раничение — о раничение по времени использова-
ния ресрсов. Рассмотрим ресрс C
1
— выпсая 1 шт. изделий B
1
,
ресрс C
1
необходимо использовать 1 час, а все о бдет выпсать-
ся X
1
шт, следовательно, для выпса всех изделий вида B
1
ре-
срс C
1
бдет занят 1 × X
1
часов, но ресрс C
1
занят таже и выпс-
ом B
2
. То да полное время занятости ресрса C
1
бдет X
1
+ 2X
2
, но,
по словию, масимально возможное время использования ре-
срса C
1
не может превышать 8 часов, значит,
X
1
+ 2X
2
m 8. (9.7)
Совершенно анало ично расписывается о раничение и по ис-
пользованию ресрса C
2
:
2X
1
+ X
2
m 10. (9.8)
Ита, требется найти таие значения X
1
и X
2
(таие планы,
таие правляющие воздействия), оторые бы, довлетворяя о -
раничениям (9.6—9.8) (оторые определяют область допстимых
значений правляющих воздействий), обращали бы в масимм
выражение (9.5) (ритерий эффетивности). И, оончательно,
5X
1
+ 3X
2
= F → max при .
Модели алендарноо планирования. Эти модели порядочи-
вают во времени выполнение аих-либо работ или событий.
Математичесим аппаратом моделей алендарно о планирова-
ния является теория расписаний. Рассмотрим типичный пример
моделей алендарно о планирования.
Псть имеется m деталей, подлежащих обработе; обработа
идет на n станах: i = , j = . Маршрт обработи, то есть
порядо прохождения аждой детали станов, всех деталей оди-
2X
1
+ X
2
m 10,
X
1
+ 2X
2
m 8,
X
1
l 0,
X
2
l 0
1 m,
1 n,
479
наов, но время обработи естественно различное. Требется
порядочить очередь деталей на входе, т.е. определить таю пос-
ледовательность запса деталей в производство, оторая мини-
мизировала бы сммарное время обработи всех деталей.
Эт задач можно проиллюстрировать рисном 9.5.
Уазанная задача решается при следющих о раничениях: для
аждой детали i ее обработа на стане j может начаться не ранее,
чем она заончится на стане (j-1). Если t
ij
— время начала обра-
боти i-той детали на j-том стане; — время оончания об-
работи i-той детали на j-том стане, то можно записать:
t
ij
l ,
на аждом стане одновременно может обрабатываться тольо
одна деталь.
Процесс обработи детали не прерывается до полно о е о за-
вершения
= t
ij
+ t
ij
.
В настоящее время азанная задача стро о решена тольо
для слчая двх станов. При n > 2 использются либо эвристи-
чесие приемы, не арантирющие отысания лобально о эс-
тремма, либо перебор всех возможных ситаций.
Пример. Псть n = 2. В этом слчае может быть использован ал-
оритм Джонсона. Обозначим для простоты t
i,1
через a
i
, t
i,2
через b
i
.
Первый ша алоритма. Среди чисел (a
1
, a
2
, …, a
m
, b
1
, b
2
, …, b
i
,
…, b
m
) ищется наименьшее число. Если этим числом оазывается
число a
i
, то пола ают i = i
1
, т. е. помещают i-тю деталь на первое
место в расписании. Если наименьшим числом оазалось число
b
i
, то пола ают i = i
m
, т. е. помещают i-тю деталь на последнее
место в расписании. Если а в 1-м, та и во 2-м слчае оазалось
несольо равных чисел, то берт любое из них, затем деталь i
вычеривается из расписания (т. е. вычериваются числа (a
i
, b
i
)).
k-тый ша алоритма (1<k<m): Среди оставшихся чисел, еще
не вычернтых на предыдщих ша ах, находим наименьшее
2 3
{i}
1
t
i1
t
i2
t
i3
n = 3, i = 1, m
Рис. 9.5. Модель алендарноо планирования
t
ij 1−()
t
ij 1−()
t
ij
480
число. Если им оазалось число a
i
, то помещаем деталь i на пер-
вое место из мест еще не занятых в списе. Если им оазалось
число b
i
, то помещаем на последнее еще не занятое место в спис-
е; вычериваем деталь i из списа.
m-ный ша алоритма (последний): Помещаем единственню
оставшюся деталь на единственное свободное место.
Рассмотрим числовой пример: псть время обработи деталей
задано табл. 9.1.
Табл иц а 9 .1
Таим образом, оптимальное расписание opt < i
1
, i
2
, i
3
, i
4
, i
5
,
i
6
> = < 2, 3, 1, 4, 6, 5 >. Перебор потребовал бы просмотра
6! = 720 вариантов.
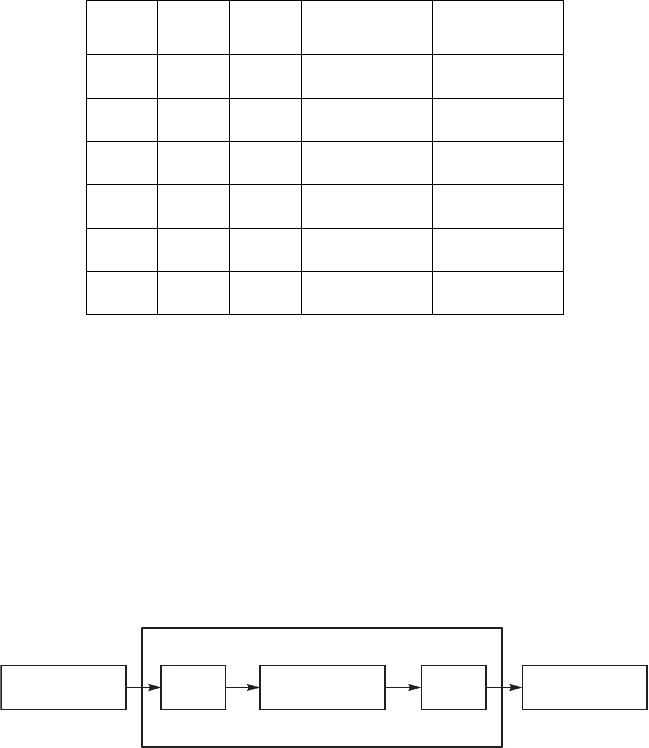
Модели правления запасами. Запас — это всяое неиспольз-
емое в данный момент времени средство, имеющее эономичес-
ю ценность. Из это о определения следет, что на данный запас
все да пристствет спрос. Запас пополняется посредством пос-
тплений (рис. 9.6).
Эономичесой единицей мо т быть часто, цех, предпри-
ятие, объединение, отрасль. Дисретность поставо, сбои произ-
i
a
i
b
i
Номер шаа
Место детали
в расписании
189 V i
1
= 3
235 I i
2
= 1
346 II i
3
= 2
4109 VI i
4
= 4
574 III i
5
= 6
675 IV i
6
= 5
ÑêëàäÏîñòàâùèê Ïðîèçâîäñòâî
Ýêîíîìè÷åñêàÿ åäèíèöà
Ñêëàä Ïîòðåáèòåëü
a(t) b(t)
Рис. 9.6. Стртра модели правления запасами
481
водства, слчайные олебания в спросе вынждают эономичес-
ю единиц создавать запас своей продции с тем, чтобы не
подвер ать потребителя рис простоя, посоль в этой сита-
ции эономичесая единица вынждена платить нестойи или
штраф. С др ой стороны, наопление чрезмерных запасов при-
водит излишним затратам на их хранение, запасы морально и
физичеси старевают. Все это приводит омертвлению до (50%)
апитала.
Таим образом, основной задачей правления запасами явля-
ется определение минимально о ровня запаса при довлетвори-
тельном снабжении всех потребителей. В данной модели произ-
водство рассматривается а процесс постпления (от поставщи-
а) и выхода ( потребителю). Постпление и выход описываются
интенсивностями a(t) и b(t).
Если ровень запаса в момент времени t = 0 есть I
0
, то в мо-
мент времени t фнция запаса I(t):
I(t) = I
0
+ dt.
Интенсивность выхода очень часто отождествляется с интен-
сивностью спроса r(t). Этой харатеристиой харатеризется
предприятие-потребитель. Фнция запаса I(t), а отмечалось
выше, вызывает появление затрат, оторые являются в общем
слчае неоторым фнционалом от a(t), b(t), r(t):
E = E{a(t), b(t), r(t)}.
Этот фнционал харатеризет эффетивность системы.
Требется найти таие значения фнций a(t), b(t), r(t), оторые
бы оптимизировали е о значение.
Рассмотрим частный слчай этой задачи, введя следющие
предположения.
Псть спрос не зависит от времени и пристствет все да.
Уменьшение запаса от спроса происходит с постоянной соро-
стью r, т. е.
∆I(t) = –r∆t, r = const.
Пополнение запаса происходит в дисретные моменты вре-
мени. Увеличение запаса от постпления происходит с неоторой
постоянной соростью p, т. е.
∆I(t) = +p∆t, p = const.
at() bt()−
[]
0
t
∫
