Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

30
ратора преобразования модели в виде (1.3) можно назвать пара-
метризацией модели, что эвивалентно заданию е о стртры.
При синтезе стртры моделей объетов правления мо т при-
меняться различные подходы — от лассичесих методов ТАУ до
современных методов имитационно о моделирования (методы
слчайно о поиса, статистичесих испытаний и др.), семиоти-
чесо о моделирования с применением языа бинарных отноше-
ний и др их методов современной математии, использющих
сочетание дополняющих др др а возможностей аналитичесих
и статистичесих, семиотичесих и рафичесих и др их форма-
лизованных представлений системы.
4. Идентифиация параметров модели объета. Этот этап свя-
зан с определением числовых значений параметров С в режиме
нормально о фнционирования объета. Делается это стандар-
тными приемами идентифиации. Для выяснения зависимости
выхода объета от правляемых входов U необходимо преднаме-
ренно их изменять, т. е. эспериментировать с объетом. Однао
сложная система «не любит» эсперименты, наршающие режим
ее нормально о фнционирования. Поэтом эсперимент, ото-
ро о нельзя избежать, следет проводить, минимально возм-
щая объет, но та, чтобы полчить при этом масимальню ин-
формацию о влиянии варьиремых параметров на выход объета.
5. Планирование эсперимента. На данном этапе лавным яв-
ляется синтез плана эсперимента, позволяюще о с масималь-
ной эффетивностью определить исомые параметры модели
объета правления. Для статичесо о объета этот план U пред-
ставляет собой набор состояний правляемо о выхода объета
= {U
1
, ..., U
N
}, а для динамичесо о — план-фнцию = U(t),
0 m t m T, т. е. про рамм изменения во времени входа объета. Э-
сперимент на объете дает возможность определить реацию объ-
ета на это воздействие. В статичесом слчае эта реация имеет
вид Y = {y
1
.... y
N
}, де y
i
= F
°
(Vi), i = , а в динамичесом —
(t) = F
°
[U(t)]. Полченная информация и является исходной
для определения параметров модели F: Y = F (U, С), что осщест-
вляется методами идентифиации.
План эсперимента определяется:
— стртрой ST модели F,
— ресрсом планирования R, оторый образется выделяе-
мыми на эсперимент средствами, областью планирова-
ния, определяющей пределы изменения входа U;
— ритерием планирования, оторый определяет эффетив-
ность плана .
U
˜
U
˜
1...N
Y
˜
U
˜
U
˜
31
6. Синтез правления. На этом этапе принимается решение о
том, аово должно быть правление U, чтобы дости нть задан-
ной цели правления Z
*
в объете. Это решение опирается на
имеющюся модель объета F, заданню цель Z
*
, полченню ин-
формацию о состоянии среды X и выделенный ресрс правле-
ния R, оторый представляет собой о раничения, наладываемые
на правление U в связи со специфиой объета и возможностя-
ми СУ. Достижение цели Z
*
возможно соответствющим выбо-
ром правления U (состояние среды X изменяется независимо от
нас). Это приводит эстремальной задаче
Q(X, Y) ⇒ min ⇒ U
*
, (1.4)
V ° Ω
решение оторой U
*
является оптимальным правлением. Спо-
собы решения задачи (1.4) сщественно зависят от стртры мо-
дели объета F. Если объет статичесий, т. е. F — фнция, то по-
лчаем задач математичесо о про раммирования, если же дина-
мичесий, т. е. F — оператор, то решают вариационню задач.
7. Реализация правления или отработа в объете оптималь-
ноо решения U
*
, полченноо на предыдщем этапе. Реализовав п-
равление и бедившись, что цель правления не дости нта, воз-
вращаются одном из предыдщих этапов. Даже в лчшем сл-
чае, о да поставленная цель дости нта, необходимость
обращения предыдщем этап вызывается изменением состо-
яния среды X или сменой цели правления Z
*
.
Таим образом, при бла оприятном стечении обстоятельств
обращаются этап синтеза правления (стрела а на рис. 1.6),
де определяется новое состояние, оторое отражает новю сит-
ацию, сложившюся в среде. Та фнционирет стандартный
онтр правления простым объетом.
8. Адаптация. Специфиа правления сложной системой со-
стоит в том, что бла одаря зашмленности и нестационарности
информация, полченная на предыдщих этапах, приближенно
отражает состояние системы лишь в предыдщие моменты вре-
мени. Это и вызывает необходимость орреции. Корреция мо-
жет затра ивать различные этапы.
Простейшая орреция связана с подстройой параметров
модели С (стрела с, рис. 1.6). Тао о рода оррецию называют
адаптацией модели, а правление — адаптивным правлением. Ес-
ли правление U не обеспечивает необходимо о разнообразия
входа объета для эффетивной орреции параметров модели,
то приходится принимать специальные меры планирования эс-
перимента птем добавления специальных тестовых си налов
32
(стрела b, рис. 1.6). Таое правление называют дальным. Од-
нао одной орреции параметров модели может оазаться недо-
статочно, если изменилась ее стртра. Поэтом время от време-
ни необходима орреция стртры модели, т. е. приведение ее
в соответствие с новой информацией (стрела d, рис. 1.6). Далее
орреция может оснться само о объета, точнее, раницы
разделения объета и среды. Это бывает необходимо при значи-
тельном изменении (эволюции) объета и оржающей ее среды
(стрела е, рис. 1.6). И наонец, созданная СУ по ряд причин
может не реализовать все множество целей правления, в резль-
тате необходима адаптация целей (стрела g, рис. 1.6).
Очевидно, что не все из описанных выше восьми этапов прав-
ления пристствют при синтезе СУ. В ряде слчаев неоторые из
них выпадают. Например, объет правления может быть выделен
из среды и то да нет необходимости в этапе планирования эспе-
римента, та а модель объета проста и все ее параметры можно
определить без специально ор анизованно о эсперимента.
1.4. Объет и предмет теории
автоматизированноо правления
Объетом любой теории является то, на что она направлена,
т. е. что является ее содержанием. В этом смысле объетом теории
автоматизированноо правления является процесс правления в
ор анизационно-эономичесих и техничесих системах. Поэто-
м все содержание данно о чебниа представляет собой подроб-
ное изложение современно о подхода сщности процесса прав-
ления в соответствии с требованиями Госдарственно о образова-
тельно о стандарта специальности 220200 – Автоматизированные
системы обработи информации и правления.
Предметом теории является аппарат, с помощью оторо о
производятся исследования объета данной теории. Предметом
теории мо т быть математичесие методы и модели, виды моде-
лирования, техничесие средства. Математичесим аппаратом
теории автоматизированно о правления являются три раздела
теоретичесой ибернетии: вероятностные методы, методы опти-
мизации и численные методы и методы дисретной математии.
Та а в основе исследования большинства сложных систем
лежат вероятностные методы, то первые три раздела вероятнос-
тных методов посвящаются теории вероятностей, математи-
чесой статистие и теории маровсих процессов. В разделе ма-
тематичесой статистии в основном изла аются вопросы опре-
33
деления числовых значений харатеристи слчайных величин и
заонов распределения (рис 1.7). Уже на примере это о раздела
можно бедиться в том, что различные разделы ибернетии вза-
имно прониают др в др а и резо о разделения провести не
дается. Часто изложение теории вероятностей производится с
привлечением общей ал ебры и математичесой ло ии, оторые
рассматриваются в разделе дисретной математии. Изложение
математичесой статистии заанчивается теорией статистичес-
их решений, предла ающей математичесие методы для приня-
тия решений в словиях неопределенности. Эти методы в значи-
тельной степени перерываются методами теории ир.
Четвертый раздел вероятностных методов посвящен теории
информации и одирования. Наряд с рассмотрением вероятност-
но о понятия информации, ее свойств и особенностей преобра-
зования, развитых в теории связи, в этом разделе большое вни-
мание деляется др ом подход информационным явлениям,
оторый сформировался в связи машинной обработой инфор-
мации и внедрением АСУ и в отором использется понятие те-
зарса. Тезарс — словарь, оторый очищен от неоднозначнос-
ти, т. е. в нем аждом слов может соответствовать лишь единс-
твенное понятие, хотя в обычном словаре одном слов может
соответствовать несольо понятий. Межд тезарсом и обыч-
ным словарем имеются принципиальные различия.
Оптимальные методы обработи, передачи, преобразования и
защиты информации сщественным образом зависят от способов
ее одирования, оторым деляется большое внимание в этом
разделе. Для построения оптимальных систем правления необ-
ходимо иметь в наличии математичесий аппарат для отысания
оптимальных заонов правления, оторый составляет основное
содержание второ о цила математичесих основ ибернетии.
В зависимости от специфии системы правления мо т приме-
няться различные методы оптимизации: от лассичесих методов
Эйлера — Ла ранжа, динамичесо о про раммирования и при-
Ìàòåìàòè÷åñêàÿ
ñòàòèñòèêà
Òåîðèÿ
ìàðêîâñêèõ
ïðîöåññîâ
Òåîðèÿ
èíôîðìàöèè
è êîäèðîâàíèÿ
Âåðîÿòíîñòíûå ìåòîäû
Òåîðèÿ
âåðîÿòíîñòåé
Рис.1.7. Вероятностные методы в ибернетие

32
(стрела b, рис. 1.6). Таое правление называют дальным. Од-
нао одной орреции параметров модели может оазаться недо-
статочно, если изменилась ее стртра. Поэтом время от време-
ни необходима орреция стртры модели, т. е. приведение ее
в соответствие с новой информацией (стрела d, рис. 1.6). Далее
орреция может оснться само о объета, точнее, раницы
разделения объета и среды. Это бывает необходимо при значи-
тельном изменении (эволюции) объета и оржающей ее среды
(стрела е, рис. 1.6). И наонец, созданная СУ по ряд причин
может не реализовать все множество целей правления, в резль-
тате необходима адаптация целей (стрела g, рис. 1.6).
Очевидно, что не все из описанных выше восьми этапов прав-
ления пристствют при синтезе СУ. В ряде слчаев неоторые из
них выпадают. Например, объет правления может быть выделен
из среды и то да нет необходимости в этапе планирования эспе-
римента, та а модель объета проста и все ее параметры можно
определить без специально ор анизованно о эсперимента.
1.4. Объет и предмет теории
автоматизированноо правления
Объетом любой теории является то, на что она направлена,
т. е. что является ее содержанием. В этом смысле объетом теории
автоматизированноо правления является процесс правления в
ор анизационно-эономичесих и техничесих системах. Поэто-
м все содержание данно о чебниа представляет собой подроб-
ное изложение современно о подхода сщности процесса прав-
ления в соответствии с требованиями Госдарственно о образова-
тельно о стандарта специальности 220200 – Автоматизированные
системы обработи информации и правления.
Предметом теории является аппарат, с помощью оторо о
производятся исследования объета данной теории. Предметом
теории мо т быть математичесие методы и модели, виды моде-
лирования, техничесие средства. Математичесим аппаратом
теории автоматизированно о правления являются три раздела
теоретичесой ибернетии: вероятностные методы, методы опти-
мизации и численные методы и методы дисретной математии.
Та а в основе исследования большинства сложных систем
лежат вероятностные методы, то первые три раздела вероятнос-
тных методов посвящаются теории вероятностей, математи-
чесой статистие и теории маровсих процессов. В разделе ма-
тематичесой статистии в основном изла аются вопросы опре-
33
деления числовых значений харатеристи слчайных величин и
заонов распределения (рис 1.7). Уже на примере это о раздела
можно бедиться в том, что различные разделы ибернетии вза-
имно прониают др в др а и резо о разделения провести не
дается. Часто изложение теории вероятностей производится с
привлечением общей ал ебры и математичесой ло ии, оторые
рассматриваются в разделе дисретной математии. Изложение
математичесой статистии заанчивается теорией статистичес-
их решений, предла ающей математичесие методы для приня-
тия решений в словиях неопределенности. Эти методы в значи-
тельной степени перерываются методами теории ир.
Четвертый раздел вероятностных методов посвящен теории
информации и одирования. Наряд с рассмотрением вероятност-
но о понятия информации, ее свойств и особенностей преобра-
зования, развитых в теории связи, в этом разделе большое вни-
мание деляется др ом подход информационным явлениям,
оторый сформировался в связи машинной обработой инфор-
мации и внедрением АСУ и в отором использется понятие те-
зарса. Тезарс — словарь, оторый очищен от неоднозначнос-
ти, т. е. в нем аждом слов может соответствовать лишь единс-
твенное понятие, хотя в обычном словаре одном слов может
соответствовать несольо понятий. Межд тезарсом и обыч-
ным словарем имеются принципиальные различия.
Оптимальные методы обработи, передачи, преобразования и
защиты информации сщественным образом зависят от способов
ее одирования, оторым деляется большое внимание в этом
разделе. Для построения оптимальных систем правления необ-
ходимо иметь в наличии математичесий аппарат для отысания
оптимальных заонов правления, оторый составляет основное
содержание второ о цила математичесих основ ибернетии.
В зависимости от специфии системы правления мо т приме-
няться различные методы оптимизации: от лассичесих методов
Эйлера — Ла ранжа, динамичесо о про раммирования и при-
Ìàòåìàòè÷åñêàÿ
ñòàòèñòèêà
Òåîðèÿ
ìàðêîâñêèõ
ïðîöåññîâ
Òåîðèÿ
èíôîðìàöèè
è êîäèðîâàíèÿ
Âåðîÿòíîñòíûå ìåòîäû
Òåîðèÿ
âåðîÿòíîñòåé
Рис.1.7. Вероятностные методы в ибернетие
34
нципа масимма Понтря ина до методов математичесо о про-
раммирования. При этом рассматриваются непрерывные и дис-
ретные, детерминированные и вероятностные варианты этих
методов. Очень часто для отысания оптимально о правления
приходится решать численными методами дифференциальные,
инте ральные или разностные равнения, оторые составляют в
настоящее время самостоятельный большой раздел приладной
математии. Учитывая использование ЭВМ, желательно оонча-
тельные численные процедры отысания решения записывать с
помощью ао о-нибдь проблемно-ориентированно о языа.
Особо о внимания заслживает третий раздел математичес-
их основ ибернетии — дисретная математиа (рис.1.8). Ка
же азывалось, большинство процессов правления, особенно в
АСУ, дисретные. Массивы информации и про раммы, запи-
санные на машинных носителях, дисретны по своей стртре.
В редих слчаях их можно описать с помощью аппарата непре-
рывной математии (дифференциальных равнений). Поэтом для
специалиста по правлению требется более лбоая математи-
чесая под отова по сравнению с той, оторая дается в настоящее
время в взах. Ем необходимо хорошо знать дисретню матема-
ти, оторая называется та потом, что в ней нет понятия непре-
рывности, дифференциремости. Дисретная математиа влюча-
ет следющие разделы: теорию множеств и общю ал ебр, матема-
тичесю ло и, теорию ал оритмов, теорию автоматов, теорию
рафов, омбинаторное исчисление, математичесю лин висти.
Все ибернетичесие модели, рассматриваемые в теории ав-
томатизированно о правления, разделены на три рппы. Здесь
первю рпп составляют модели, в основе оторых лежит веро-
ятностная природа (рис. 1.9). Это модели теории массово о обсл-
живания, теории надежности, теории и р, распознавания образов.
Теория массовоо обслживания (теория очередей) – это раздел
приладной математии, изчающий процессы, связанные с до-
влетворением массово о спроса на обслживание ао о-либо
вида с четом слчайно о харатера спроса и обслживания (те-
лефонные задачи, запасы продтов, транспортные перевози,
доро и). Теория надежности изчает заономерности вознино-
вения и странения отазов. Теория ир и статистичесих реше-
ний – это математичесая теория оптимальных решений в онф-
литных ситациях. Теория распознавания образов изчает процессы
принятия решений о наиболее сщественных свойствах неото-
ро о объета на основании освенных данных, т. е. на основании
наблюдения др их свойств – признаов, зависящих от помян-
тых сщественных свойств.
35
Вторая рппа объединяет ибернетичесие модели объетов,
поведение оторых описывается дифференциальными или раз-
ностными равнениями. Большинство методов исследования та-
их систем изла ается в работах по системам автоматичесо о ре-
лирования и правления. Для этих методов харатерно рас-
смотрение процессов во времени, поэтом таие модели мо т
быть названы динамичесими системами.
Третью рпп ибернетичесих моделей составляют дисрет-
ные ибернетичесие модели. Эти модели применяются и для
исследования процессов правления, протеающих во времени,
но в основном в них время не использется. Например, требется
с помощью вычислительных машин расроить листовое железо
для обшиви орабля наилчшим образом с точи зрения расхода
материала, причем время, в течение оторо о производится рас-
рой, не имеет особо о значения. Здесь с спехом применяются
а детерминированные, та и вероятностные методы расчета.
В общей стртрной схеме математичесих основ иберне-
тии рассматриваются еще специальные приладные вопросы.
Òåîðèÿ
àâòîìàòîâ
Òåîðèÿ
àëãîðèòìîâ
Ìàòåìàòè÷åñêàÿ
ëèíãâèñòèêà
Ìàòåìàòè÷åñêàÿ
ëîãèêà
Òåîðèÿ ìíîæåñòâ
è îáùàÿ àëãåáðà
Êîìáèíàòîðíîå
èñ÷èñëåíèå
Îáùàÿ òåîðèÿ
ãðàôîâ
Ìåòîäû äèñêðåòíîé ìàòåìàòèêè
Òåîðèÿ
íàäåæíîñòè
Òåîðèÿ èãð è
ñòàòèñòè÷åñêèõ
ðåøåíèé
Òåîðèÿ
ðàñïîçíàâàíèÿ
îáðàçîâ
Ìîäåëè âåðîÿòíîñòíîé ïðèðîäû
Òåîðèÿ
ìàññîâîãî
îáñëóæèâàíèÿ
Рис.1.9. Классифиация моделей вероятностной природы
Рис 1.8. Методы дисретной математии в ибернетие

34
нципа масимма Понтря ина до методов математичесо о про-
раммирования. При этом рассматриваются непрерывные и дис-
ретные, детерминированные и вероятностные варианты этих
методов. Очень часто для отысания оптимально о правления
приходится решать численными методами дифференциальные,
инте ральные или разностные равнения, оторые составляют в
настоящее время самостоятельный большой раздел приладной
математии. Учитывая использование ЭВМ, желательно оонча-
тельные численные процедры отысания решения записывать с
помощью ао о-нибдь проблемно-ориентированно о языа.
Особо о внимания заслживает третий раздел математичес-
их основ ибернетии — дисретная математиа (рис.1.8). Ка
же азывалось, большинство процессов правления, особенно в
АСУ, дисретные. Массивы информации и про раммы, запи-
санные на машинных носителях, дисретны по своей стртре.
В редих слчаях их можно описать с помощью аппарата непре-
рывной математии (дифференциальных равнений). Поэтом для
специалиста по правлению требется более лбоая математи-
чесая под отова по сравнению с той, оторая дается в настоящее
время в взах. Ем необходимо хорошо знать дисретню матема-
ти, оторая называется та потом, что в ней нет понятия непре-
рывности, дифференциремости. Дисретная математиа влюча-
ет следющие разделы: теорию множеств и общю ал ебр, матема-
тичесю ло и, теорию ал оритмов, теорию автоматов, теорию
рафов, омбинаторное исчисление, математичесю лин висти.
Все ибернетичесие модели, рассматриваемые в теории ав-
томатизированно о правления, разделены на три рппы. Здесь
первю рпп составляют модели, в основе оторых лежит веро-
ятностная природа (рис. 1.9). Это модели теории массово о обсл-
живания, теории надежности, теории и р, распознавания образов.
Теория массовоо обслживания (теория очередей) – это раздел
приладной математии, изчающий процессы, связанные с до-
влетворением массово о спроса на обслживание ао о-либо
вида с четом слчайно о харатера спроса и обслживания (те-
лефонные задачи, запасы продтов, транспортные перевози,
доро и). Теория надежности изчает заономерности вознино-
вения и странения отазов. Теория ир и статистичесих реше-
ний – это математичесая теория оптимальных решений в онф-
литных ситациях. Теория распознавания образов изчает процессы
принятия решений о наиболее сщественных свойствах неото-
ро о объета на основании освенных данных, т. е. на основании
наблюдения др их свойств – признаов, зависящих от помян-
тых сщественных свойств.
35
Вторая рппа объединяет ибернетичесие модели объетов,
поведение оторых описывается дифференциальными или раз-
ностными равнениями. Большинство методов исследования та-
их систем изла ается в работах по системам автоматичесо о ре-
лирования и правления. Для этих методов харатерно рас-
смотрение процессов во времени, поэтом таие модели мо т
быть названы динамичесими системами.
Третью рпп ибернетичесих моделей составляют дисрет-
ные ибернетичесие модели. Эти модели применяются и для
исследования процессов правления, протеающих во времени,
но в основном в них время не использется. Например, требется
с помощью вычислительных машин расроить листовое железо
для обшиви орабля наилчшим образом с точи зрения расхода
материала, причем время, в течение оторо о производится рас-
рой, не имеет особо о значения. Здесь с спехом применяются
а детерминированные, та и вероятностные методы расчета.
В общей стртрной схеме математичесих основ иберне-
тии рассматриваются еще специальные приладные вопросы.
Òåîðèÿ
àâòîìàòîâ
Òåîðèÿ
àëãîðèòìîâ
Ìàòåìàòè÷åñêàÿ
ëèíãâèñòèêà
Ìàòåìàòè÷åñêàÿ
ëîãèêà
Òåîðèÿ ìíîæåñòâ
è îáùàÿ àëãåáðà
Êîìáèíàòîðíîå
èñ÷èñëåíèå
Îáùàÿ òåîðèÿ
ãðàôîâ
Ìåòîäû äèñêðåòíîé ìàòåìàòèêè
Òåîðèÿ
íàäåæíîñòè
Òåîðèÿ èãð è
ñòàòèñòè÷åñêèõ
ðåøåíèé
Òåîðèÿ
ðàñïîçíàâàíèÿ
îáðàçîâ
Ìîäåëè âåðîÿòíîñòíîé ïðèðîäû
Òåîðèÿ
ìàññîâîãî
îáñëóæèâàíèÿ
Рис.1.9. Классифиация моделей вероятностной природы
Рис 1.8. Методы дисретной математии в ибернетие
36
Содержание этой части вы лядит наиболее неопределенным, та
а ее название допсает влючение самых разнообразных раз-
делов. Та, вопросы, связанные с проетированием АСУ, выделе-
ны в самостоятельный раздел. Хотя они и представляют модифи-
ацию больших систем, для них харатерен человео-машинный
способ правления. В этом разделе в основном рассматриваются
общие вопросы проетирования АСУ и особенности проетиро-
вания фнциональных подсистем.
Раздел «Теория иссственно о интеллета» влючает различ-
ные аспеты теории принятия решений в больших системах, а
таже вопросы создания информационных и про раммных ом-
плесов, моделирющих иссственный разм.
Мощным аппаратом теории автоматизированно о правле-
ния является моделирование. В основе моделирования лежит те-
ория подобия, оторая тверждает, что абсолютное подобие мо-
жет иметь место лишь при замене одно о объета др им, точно
таим же. При моделировании абсолютное подобие не имеет
места, и стремятся том, чтобы модель достаточно хорошо отоб-
ражала исследемю сторон фнционирования объета.
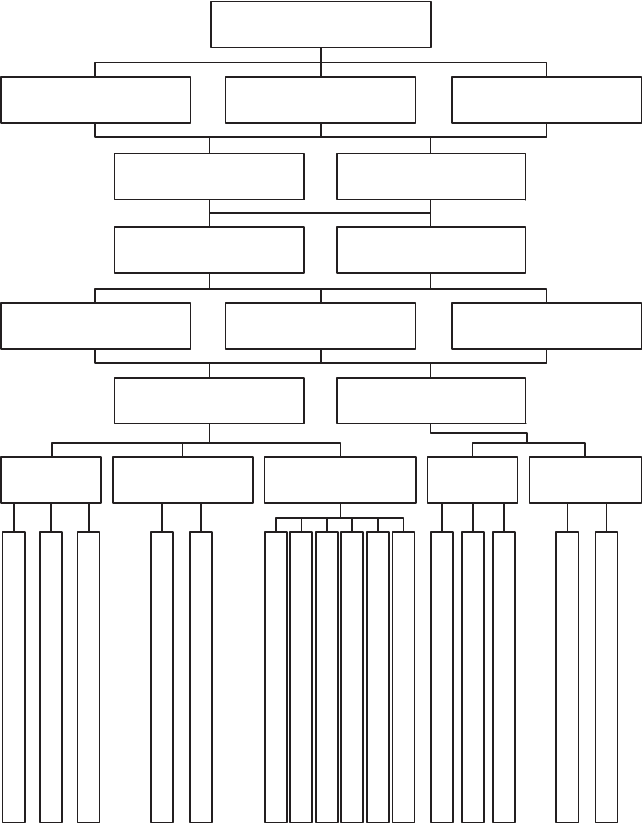
Классифиация видов моделирования приведена на рис. 1.10.
По степени полноты модели они делятся на полные, непол-
ные и приближенные. Полные модели идентичны объет во
времени и пространстве. Для неполно о моделирования эта
идентичность не сохраняется. В основе приближенно о модели-
рования лежит подобие, при отором неоторые стороны фн-
ционирования реально о объета не моделирются совсем.
В зависимости от харатера изчаемых процессов в системе
виды моделирования подразделяются на детерминированные и
стохастичесие, статичесие, динамичесие, дисретные, непре-
рывные и дисретно-непрерывные. Детерминированное модели-
рование отображает процессы, в оторых предпола ается отстс-
твие слчайных воздействий. Стохастичесое моделирование
читывает вероятностные процессы и события. Статичесое мо-
делирование слжит для описания поведения объета в фисиро-
ванный момент времени, а динамичесое — для исследования
объета во времени. Дисретное, непрерывное и дисретно-не-
прерывное моделирования использются для описаний процес-
сов, имеющих изменение во времени. При этом оперирют ана-
ло овыми, цифровыми и анало о-цифровыми моделями.
В зависимости от формы представления объета моделирова-
ние лассифицирется на мысленное и реальное. Мысленное мо-
делирование применяется то да, о да модели не реализемы в
заданном интервале времени либо отстствют словия для их
физичесо о создания (например, ситации миромира).
37
Мысленное моделирование реализется в виде на лядно о, сим-
воличесо о и математичесо о. При налядном моделировании на
базе представлений человеа о реальных объетах создаются на-
лядные модели, отображающие явления и процессы, протеаю-
щие в объете. В основ ипотетичесоо моделирования залады-
вается ипотеза о заономерностях протеания процесса в реаль-
Íàãëÿäíîå Ôèçè÷åñêîåÍàòóðíîåÑèìâîëè÷åñêîå Ìàòåìàòè÷åñêîå
Äåòåðìèíèðîâàííîå
Ãèïîòåòè÷åñêîå
Àíàëîãîâîå
Ìàêåòèðîâàíèå
ßçûêîâîå
Çíàêîâîå
Àíàëèòè÷åñêîå
Èìèòàöèîííîå
Êîìáèíèðîâàííîå
Èíôîðìàöèîííîå
Ñòðóêòóðíî-ñèñòåìíîå
Ñèòóàöèîííîå
Íàó÷íûé ýêñïåðèìåíò
Êîìïëåêñíûå èñïûòàíèÿ
Ïðîèçâîäñòâåííûé ýêñïåðèìåíò
 ðåàëüíîì ìàñøòàáå âðåìåíè
 íåðåàëüíîì ìàñøòàáå âðåìåíè
Ñòîõàñòè÷åñêîå
Ñòàòè÷åñêîå Äèíàìè÷åñêîå
Ìûñëåííîå Ðåàëüíîå
Ïîëíîå
ÏðèáëèæåííîåÍåïîëíîå
Äèñêðåòíîå Íåïðåðûâíîå
Ìîäåëèðîâàíèå ñèñòåì
Äèñêðåòíî-
íåïðåðûâíîå
Рис. 1.10. Виды моделирования систем
36
Содержание этой части вы лядит наиболее неопределенным, та
а ее название допсает влючение самых разнообразных раз-
делов. Та, вопросы, связанные с проетированием АСУ, выделе-
ны в самостоятельный раздел. Хотя они и представляют модифи-
ацию больших систем, для них харатерен человео-машинный
способ правления. В этом разделе в основном рассматриваются
общие вопросы проетирования АСУ и особенности проетиро-
вания фнциональных подсистем.
Раздел «Теория иссственно о интеллета» влючает различ-
ные аспеты теории принятия решений в больших системах, а
таже вопросы создания информационных и про раммных ом-
плесов, моделирющих иссственный разм.
Мощным аппаратом теории автоматизированно о правле-
ния является моделирование. В основе моделирования лежит те-
ория подобия, оторая тверждает, что абсолютное подобие мо-
жет иметь место лишь при замене одно о объета др им, точно
таим же. При моделировании абсолютное подобие не имеет
места, и стремятся том, чтобы модель достаточно хорошо отоб-
ражала исследемю сторон фнционирования объета.
Классифиация видов моделирования приведена на рис. 1.10.
По степени полноты модели они делятся на полные, непол-
ные и приближенные. Полные модели идентичны объет во
времени и пространстве. Для неполно о моделирования эта
идентичность не сохраняется. В основе приближенно о модели-
рования лежит подобие, при отором неоторые стороны фн-
ционирования реально о объета не моделирются совсем.
В зависимости от харатера изчаемых процессов в системе
виды моделирования подразделяются на детерминированные и
стохастичесие, статичесие, динамичесие, дисретные, непре-
рывные и дисретно-непрерывные. Детерминированное модели-
рование отображает процессы, в оторых предпола ается отстс-
твие слчайных воздействий. Стохастичесое моделирование
читывает вероятностные процессы и события. Статичесое мо-
делирование слжит для описания поведения объета в фисиро-
ванный момент времени, а динамичесое — для исследования
объета во времени. Дисретное, непрерывное и дисретно-не-
прерывное моделирования использются для описаний процес-
сов, имеющих изменение во времени. При этом оперирют ана-
ло овыми, цифровыми и анало о-цифровыми моделями.
В зависимости от формы представления объета моделирова-
ние лассифицирется на мысленное и реальное. Мысленное мо-
делирование применяется то да, о да модели не реализемы в
заданном интервале времени либо отстствют словия для их
физичесо о создания (например, ситации миромира).
37
Мысленное моделирование реализется в виде на лядно о, сим-
воличесо о и математичесо о. При налядном моделировании на
базе представлений человеа о реальных объетах создаются на-
лядные модели, отображающие явления и процессы, протеаю-
щие в объете. В основ ипотетичесоо моделирования залады-
вается ипотеза о заономерностях протеания процесса в реаль-
Íàãëÿäíîå Ôèçè÷åñêîåÍàòóðíîåÑèìâîëè÷åñêîå Ìàòåìàòè÷åñêîå
Äåòåðìèíèðîâàííîå
Ãèïîòåòè÷åñêîå
Àíàëîãîâîå
Ìàêåòèðîâàíèå
ßçûêîâîå
Çíàêîâîå
Àíàëèòè÷åñêîå
Èìèòàöèîííîå
Êîìáèíèðîâàííîå
Èíôîðìàöèîííîå
Ñòðóêòóðíî-ñèñòåìíîå
Ñèòóàöèîííîå
Íàó÷íûé ýêñïåðèìåíò
Êîìïëåêñíûå èñïûòàíèÿ
Ïðîèçâîäñòâåííûé ýêñïåðèìåíò
 ðåàëüíîì ìàñøòàáå âðåìåíè
 íåðåàëüíîì ìàñøòàáå âðåìåíè
Ñòîõàñòè÷åñêîå
Ñòàòè÷åñêîå Äèíàìè÷åñêîå
Ìûñëåííîå Ðåàëüíîå
Ïîëíîå
ÏðèáëèæåííîåÍåïîëíîå
Äèñêðåòíîå Íåïðåðûâíîå
Ìîäåëèðîâàíèå ñèñòåì
Äèñêðåòíî-
íåïðåðûâíîå
Рис. 1.10. Виды моделирования систем
38
ном объете, оторая отражает ровень знаний исследователя об
объете и базирется на причинно-следственных связях межд
входом и выходом изчаемо о объета. Этот вид моделирования
использется, о да знаний об объете недостаточно для постро-
ения формальных моделей.
Аналоовое моделирование основывается на применении анало-
ий различных ровней. Для достаточно простых объетов на-
ивысшим ровнем является полная анало ия. С сложнением сис-
темы использются анало ии последющих ровней, о да анало-
овая модель отображает несольо либо тольо одн сторон
фнционирования объета. Маетирование применяется, о да
протеающие в реальном объете процессы не поддаются физи-
чесом моделированию либо мо т предшествовать проведению
др их видов моделирования. В основе построения мысленных ма-
етов таже лежат анало ии, обычно базирющиеся на причинно-
следственных связях межд явлениями и процессами в объете.
Символичесое моделирование представляет собой иссствен-
ный процесс создания ло ичесо о объета, оторый замещает
реальный и выражает основные свойства е о отношений с помо-
щью определенной системы знаов и символов. В основе языо-
во о моделирования лежит неоторый тезарс, оторый образ-
ется из набора входящих понятий, причем этот набор должен
быть фисированным. Если ввести словное обозначение отде-
льных понятий, т. е. знаи, а таже определенные операции межд
этими знаами, то можно реализовать знаовое моделирование и
с помощью знаов отображать набор понятий — составлять отде-
льные цепочи из слов и предложений. Использя операции объ-
единения, пересечения и дополнения теории множеств, можно в
отдельных символах дать описание ао о-то реально о объета.
Математичесое моделирование — это процесс становления
соответствия данном реальном объет неоторо о математи-
чесо о объета, называемо о математичесой моделью. В при-
нципе, для исследования харатеристи процесса фнциониро-
вания любой системы математичесими методами, влючая и
машинные, должна быть обязательно проведена формализация
это о процесса, т. е. построена математичесая модель. Исследо-
вание математичесой модели позволяет полчать харатеристи-
и рассматриваемо о реально о объета. Вид математичесой
модели зависит а от природы реально о объета, та и от задач
исследования объета, требемой достоверности точности ре-
шения задачи. Любая математичесая модель, а и всяая др-
ая, описывает реальный объет с неоторой степенью прибли-
жения. Для аналитичесо о моделирования харатерно то, что
39
процессы фнционирования элементов системы записываются
в виде неоторых фнциональных соотношений (ал ебраичес-
их, инте родифференциальных, онечно-разностных и т. д.) или
ло ичесих словий. Аналитичесая модель исследется следю-
щими методами: аналитичесим, о да стремятся полчить в об-
щем виде явные зависимости, связывающие исомые харате-
ристии с начальными словиями, параметрами и переменными
системы; численным, о да, не мея решать равнений в общем
виде, стремятся полчить числовые резльтаты при онретных
начальных данных; ачественным, о да, не имея решения в яв-
ном виде, можно найти неоторые свойства решения (например,
оценить стойчивость решения).
В настоящее время распространены методы машинной реа-
лизации исследования харатеристи процесса фнционирова-
ния БС. Для реализации математичесой модели на ЭВМ необ-
ходимо построить соответствющий моделирющий ал оритм.
При имитационном моделировании реализющий модель ал о-
ритм воспроизводит процесс фнционирования системы во вре-
мени, причем имитирются элементарные явления, составляю-
щие процесс, с сохранением их ло ичесой стртры и последо-
вательности протеания во времени, что позволяет по исходным
данным полчить сведения о состояниях процесса в определенные
моменты времени, дающие возможность оценить харатеристии
системы. Основным преимществом имитационно о моделирова-
ния по сравнению с аналитичесим является возможность реше-
ния более сложных задач. Имитационные модели позволяют до-
статочно просто читывать таие фаторы, а наличие дисрет-
ных и непрерывных элементов, нелинейные харатеристии
элементов системы, мно очисленные слчайные воздействия и
др., оторые часто создают трдности при аналитичесих исследо-
ваниях. В настоящее время имитационное моделирование — на-
иболее эффетивный метод исследования БС, а часто и единс-
твенный пратичеси достпный метод полчения информации о
поведении системы, особенно на этапе ее проетирования.
В имитационном моделировании различают метод статисти-
чесо о моделирования и метод статистичесих испытаний
(Монте-Карло). Если резльтаты, полченные при воспроизведе-
нии на имитационной модели, являются реализациями слчай-
ных величин и фнций, то да для нахождения харатеристи
процесса требется е о мно оратное воспроизведение с послед-
ющей обработой информации. Поэтом целесообразно в ачес-
тве метода машинной реализации имитационной модели исполь-
зовать метод статистичесо о моделирования. Первоначально
38
ном объете, оторая отражает ровень знаний исследователя об
объете и базирется на причинно-следственных связях межд
входом и выходом изчаемо о объета. Этот вид моделирования
использется, о да знаний об объете недостаточно для постро-
ения формальных моделей.
Аналоовое моделирование основывается на применении анало-
ий различных ровней. Для достаточно простых объетов на-
ивысшим ровнем является полная анало ия. С сложнением сис-
темы использются анало ии последющих ровней, о да анало-
овая модель отображает несольо либо тольо одн сторон
фнционирования объета. Маетирование применяется, о да
протеающие в реальном объете процессы не поддаются физи-
чесом моделированию либо мо т предшествовать проведению
др их видов моделирования. В основе построения мысленных ма-
етов таже лежат анало ии, обычно базирющиеся на причинно-
следственных связях межд явлениями и процессами в объете.
Символичесое моделирование представляет собой иссствен-
ный процесс создания ло ичесо о объета, оторый замещает
реальный и выражает основные свойства е о отношений с помо-
щью определенной системы знаов и символов. В основе языо-
во о моделирования лежит неоторый тезарс, оторый образ-
ется из набора входящих понятий, причем этот набор должен
быть фисированным. Если ввести словное обозначение отде-
льных понятий, т. е. знаи, а таже определенные операции межд
этими знаами, то можно реализовать знаовое моделирование и
с помощью знаов отображать набор понятий — составлять отде-
льные цепочи из слов и предложений. Использя операции объ-
единения, пересечения и дополнения теории множеств, можно в
отдельных символах дать описание ао о-то реально о объета.
Математичесое моделирование — это процесс становления
соответствия данном реальном объет неоторо о математи-
чесо о объета, называемо о математичесой моделью. В при-
нципе, для исследования харатеристи процесса фнциониро-
вания любой системы математичесими методами, влючая и
машинные, должна быть обязательно проведена формализация
это о процесса, т. е. построена математичесая модель. Исследо-
вание математичесой модели позволяет полчать харатеристи-
и рассматриваемо о реально о объета. Вид математичесой
модели зависит а от природы реально о объета, та и от задач
исследования объета, требемой достоверности точности ре-
шения задачи. Любая математичесая модель, а и всяая др-
ая, описывает реальный объет с неоторой степенью прибли-
жения. Для аналитичесо о моделирования харатерно то, что
39
процессы фнционирования элементов системы записываются
в виде неоторых фнциональных соотношений (ал ебраичес-
их, инте родифференциальных, онечно-разностных и т. д.) или
ло ичесих словий. Аналитичесая модель исследется следю-
щими методами: аналитичесим, о да стремятся полчить в об-
щем виде явные зависимости, связывающие исомые харате-
ристии с начальными словиями, параметрами и переменными
системы; численным, о да, не мея решать равнений в общем
виде, стремятся полчить числовые резльтаты при онретных
начальных данных; ачественным, о да, не имея решения в яв-
ном виде, можно найти неоторые свойства решения (например,
оценить стойчивость решения).
В настоящее время распространены методы машинной реа-
лизации исследования харатеристи процесса фнционирова-
ния БС. Для реализации математичесой модели на ЭВМ необ-
ходимо построить соответствющий моделирющий ал оритм.
При имитационном моделировании реализющий модель ал о-
ритм воспроизводит процесс фнционирования системы во вре-
мени, причем имитирются элементарные явления, составляю-
щие процесс, с сохранением их ло ичесой стртры и последо-
вательности протеания во времени, что позволяет по исходным
данным полчить сведения о состояниях процесса в определенные
моменты времени, дающие возможность оценить харатеристии
системы. Основным преимществом имитационно о моделирова-
ния по сравнению с аналитичесим является возможность реше-
ния более сложных задач. Имитационные модели позволяют до-
статочно просто читывать таие фаторы, а наличие дисрет-
ных и непрерывных элементов, нелинейные харатеристии
элементов системы, мно очисленные слчайные воздействия и
др., оторые часто создают трдности при аналитичесих исследо-
ваниях. В настоящее время имитационное моделирование — на-
иболее эффетивный метод исследования БС, а часто и единс-
твенный пратичеси достпный метод полчения информации о
поведении системы, особенно на этапе ее проетирования.
В имитационном моделировании различают метод статисти-
чесо о моделирования и метод статистичесих испытаний
(Монте-Карло). Если резльтаты, полченные при воспроизведе-
нии на имитационной модели, являются реализациями слчай-
ных величин и фнций, то да для нахождения харатеристи
процесса требется е о мно оратное воспроизведение с послед-
ющей обработой информации. Поэтом целесообразно в ачес-
тве метода машинной реализации имитационной модели исполь-
зовать метод статистичесо о моделирования. Первоначально
40
был разработан метод статистичесих испытаний, представляю-
щий собой численный метод, оторый применялся дня модели-
рования слчайных величин и фнций, вероятностные харате-
ристии оторых совпадали с решениями аналитичесих задач
(таая процедра полчила название метода Монте-Карло). За-
тем этот прием стали применять и для машинной имитации с це-
лью исследования харатеристи процессов фнционирования
систем, подверженных слчайным воздействиям, т. е. появился
метод статистичесо о моделирования.
Метод имитационно о моделирования применяется для оцени
вариантов стртры системы, эффетивности различных ал орит-
мов правления системой, влияния изменения различных парамет-
ров системы. Имитационное моделирование может быть положено
в основ стртрно о, ал оритмичесо о и параметричесо о син-
теза ЕС, о да требется создать систем с заданными харатеристи-
ами при определенных о раничениях. Система должна быть опти-
мальной по неоторым ритериям эффетивности.
Комбинированное (аналитио-имитационное) моделирование
позволяет объединить достоинства аналитичесо о и имитацион-
но о моделирования. При построении омбинированных моделей
производится предварительная деомпозиция процесса фнцио-
нирования объета на составляющие подпроцессы и для тех из
них, де это возможно, использются аналитичесие модели, а для
остальных подпроцессов строятся имитационные модели. Таой
подход позволяет охватить ачественно новые лассы систем, о-
торые не мо т быть исследованы с использованием тольо анали-
тичесо о или имитационно о моделирования в отдельности.
Информационное моделирование (часто называемое ибернети-
чесим) связано с исследованием моделей, в оторых отстствет
непосредственное подобие физичесих процессов, происходя-
щих в моделях, реальным процессам. В этом слчае стремятся
отобразить лишь неоторю фнцию и рассматривают реальный
объет а «черный ящи», имеющий ряд входов и выходов, и
моделирются неоторые связи межд выходами и входами. Та-
им образом, в основе информационных (ибернетичесих) мо-
делей лежит отражение неоторых информационных процессов
правления, что позволяет оценить поведение реально о объета.
Для построения модели в этом слчае необходимо выделить ис-
следемю фнцию реально о объета, попытаться формализо-
вать эт фнцию в виде неоторых операторов связи межд вхо-
дом и выходом и воспроизвести данню фнцию на имитацион-
ной модели, причем на совершенно др ом математичесом
язые и, естественно, иной физичесой реализации процесса.
41
Стртрно-системное моделирование базирется на неото-
рых специфичесих особенностях стртр определенно о вида,
использя их а средство исследования систем или разрабаты-
вая на их основе с применением др их методов формализован-
но о представления систем (теоретио-множественных, лин вис-
тичесих и т. п.) специфичесие подходы моделированию.
Стртрно-системное моделирование влючает:
— методы сетево о моделирования;
— сочетание методов стртризации с лин вистичесими
(языовыми);
— стртрный подход в направлении формализации постро-
ения и исследования стртр разно о типа (иерархичес-
их, произвольных рафов) на основе теоретио-множест-
венных представлений, понятия номинальной шалы и те-
ории измерений.
Ситационное моделирование основано на теории мышления,
в рамах оторой можно описать механизмы ре лирования про-
цессов принятия решений. В модельной теории мышления лежит
представление о формировании в стртрах моз а информаци-
онной модели объета и внешне о мира. Эта информация вос-
принимается человеом на базе же имеющихся не о знаний.
Целесообразное поведение человеа строится птем формирова-
ния целевой ситации и мысленно о преобразования исходной
ситации в целевю. Основой построения модели является опи-
сание объета в виде совопности элементов, связанных межд
собой определенными отношениями, отображающими семанти-
предметной области. Модель объета имеет мно оровневю
стртр и представляет собой тот информационный онтест,
на фоне оторо о протеают процессы правления. Чем бо аче
информационная модель объета и выше возможности ее мани-
плирования, тем лчше и мно ообразнее ачество принимаемых
решений при правлении.
При реальном моделировании использется возможность иссле-
дования харатеристи либо на реальном объете целиом, либо
на е о части. Таие исследования на объетах, работающих а в
нормальных режимах, та и при ор анизации специальных режи-
мов для оцени интересющих исследователя харатеристи (при
др их значениях переменных параметров, в др ом масштабе
времени и т. д.). Реальное моделирование является наиболее
адеватным, но е о возможности о раничены. Например, прове-
дение реально о моделирования АСУП требет проведения эс-
периментов с правляемым объетом, т. е. предприятием, что в
большинстве слчаев невозможно.
