Меньков А.В., Острейковский В.А. Теоретические основы автоматизированного управления
Подождите немного. Документ загружается.

20
В тех слчаях, о да изменение заданных значений правляе-
мых величин заранее неизвестно и о да эти величины должны
изменяться в зависимости от значений др их величин, возниа-
ет задача слежения, т. е. а можно более точно о соблюдения со-
ответствия межд тещим состоянием данной системы и состо-
янием др ой системы. Например, правление производством в
словиях изменения спроса, слежение за целью (например, само-
летом, ораблем, осмичесим объетом).
В системах оптимально о правления требется наилчшим
образом выполнить поставленню перед системой задач при за-
данных реальных словиях и о раничениях. Понятие оптималь-
ности должно быть онретизировано для аждо о отдельно о
слчая.
Прежде чем принимать решение о создании СУ, необходимо
рассмотреть все е о этапы, независимо от то о, с помощью аих
техничесих средств они бдт реализованы. Таой ал оритми-
чесий анализ правления является основой для принятия реше-
ния о создании СУ и степени ее автоматизации. При этом анали-
зе следет обязательно читывать фатор сложности объета п-
равления:
— отстствие математичесо о описания системы;
— стохастичность поведения;
— не ативность правлению;
Ïðèíÿòèå ðåøåíèÿ
Öåëü óïðàâëåíèÿ
Èíôîðìàöèîííîå
îòîáðàæåíèå
ñèòóàöèè
Ðåàëèçàöèÿ
Òåõíè÷åñêèå
ñðåäñòâà ñðåäñòâà
Îáúåêò óïðàâëåíèÿ Êàíàëû ñâÿçèÊàíàë ñâÿçè
Ïîìåõè
Ïîìåõè
Ïîìåõè
Òåõíè÷åñêèå
ñðåäñòâà
Òåõíè÷åñêèå
ñðåäñòâà
Òåõíè÷åñêèå
Îêðóæàþùàÿ ñðåäàÎêðóæàþùàÿ ñðåäà
Рис. 1.5. Система правления а совопность объетов
21
— нестационарность, дрейф харатеристи;
— невоспроизводимость эспериментов (развивающаяся
система все время а бы перестает быть сама собой, что
предъявляет специальные требования синтез и орре-
ции модели объета правления).
Особенности сложной системы часто приводят том, что
цель правления таим объетом в полной мере нио да не до-
сти ается, а бы совершенно ни было правление.
Автоматичесое и автоматизированное правление. Системы
правления делятся на два больших ласса: системы автомати-
чесо о правления (САУ) и автоматизированные системы п-
равления (АСУ). В САУ правление объетом или системой ос-
ществляется без непосредственно о частия человеа автома-
тичесими стройствами. Это замнтые системы. Основные
фнции САУ: автоматичесий онтроль и измерения, автомати-
чесая си нализация, автоматичесая защита, автоматичесие
пс и останова различных дви ателей и приводов, автоматичес-
ое поддержание заданных режимов работы обордования, авто-
матичесое ре лирование. В отличие от САУ в АСУ в сфер п-
равления влючен челове, на оторо о возла аются фнции
принятия наиболее важных решений и ответственности за при-
нятые решения. Под АСУ обычно понимают человео-машин-
ные системы, использющие современные эономио-математи-
чесие методы, средства элетронно-вычислительной технии
(ЭВТ) и связи, а таже новые ор анизационные принципы для
отысания и реализации на пратие наиболее эффетивно о п-
равления объетом (системой).
В соответствии с общепринятым представлением под автома-
тизированной системой понимается «человео-машинная систе-
ма, обеспечивающая автоматизированный сбор и обработ ин-
формации, необходимой для оптимизации правления в любых
сферах человечесой деятельности». В определении особо след-
ет выделить понятие «человео-машинная система». В автомати-
чесих системах фнции человеа сводятся разработе, отлад-
е и онтролю работы системы. Само же правление осщест-
вляется без частия человеа. В автоматизированных системах
наличие человеа (оллетива людей) в онтре правления яв-
ляется принципиальным. Челове (оллетив людей) является
лавным определяющим звеном системы правления, посоль
он принимает решения и несет за них всю ответственность —
в этом принципиальная разница межд автоматичесими и авто-
матизированными системами.
22
1.2. Терминолоия теории
автоматизированноо правления
Определение понятия «система». В настоящее время нет
единства в определении понятия «система». В первых определе-
ниях в той или иной форме оворилось о том, что система — это
элементы и связи (отношения) межд ними. Например, осново-
положни теории систем Людви фон Берталанфи определял сис-
тем а омплес взаимодействющих элементов или а сово-
пность элементов, находящихся в определенных отношениях
др с др ом и со средой. А. Холл определяет систем а мно-
жество предметов вместе со связями межд предметами и межд
их признаами. Ведтся дисссии, аой термин — «отноше-
ние» или «связь» — лчше потреблять.
Позднее в определениях системы появляется понятие цели.
Та, в «Философсом словаре» система определяется а «сово-
пность элементов, находящихся в отношениях и связях межд
собой определенным образом и образющих неоторое целост-
ное единство».
В последнее время в определение понятия системы наряд с
элементами, связями и их свойствами и целями начинают влю-
чать наблюдателя, хотя впервые на необходимость чета взаимо-
действия межд исследователем и изчаемой системой азал
один из основоположниов ибернетии У.-Р. Эшби.
М. Масарович и Я. Таахара в ни е «Общая теория систем»
считают, что система — «формальная взаимосвязь межд наблю-
даемыми признаами и свойствами».
В ачестве «рабоче о» определения понятия системы в ли-
тератре по теории систем часто рассматривается следющее:
система — множество элементов, находящихся в отношениях и
связях др с дром, оторое образет определенню целостность,
единство.
Рассмотрим основные понятия, харатеризющие строение и
фнционирование систем.
Элемент. Под элементом принято понимать простейшю не-
делимю часть системы. Ответ на вопрос, что является таой час-
тью, может быть неоднозначным и зависит от цели рассмотрения
объета а системы, от точи зрения на не о или от аспета е о
изчения. Таим образом, элемент — это предел членения систе-
мы с точи зрения решения онретной задачи и поставленной
цели. Систем можно расчленить на элементы различными спо-
собами в зависимости от формлирови цели и ее точнения в
процессе исследования.
23
Подсистема. Система может быть разделена на элементы не
сраз, а последовательным расчленением на подсистемы, ото-
рые представляют собой омпоненты более рпные, чем эле-
менты, и в то же время более детальные, чем система в целом.
Возможность деления системы на подсистемы связана с вычле-
нением совопностей взаимосвязанных элементов, способных
выполнять относительно независимые фнции, подцели, на-
правленные на достижение общей цели системы. Названием
«подсистема» подчеривается, что таая часть должна обладать
свойствами системы (в частности, свойством целостности). Этим
подсистема отличается от простой рппы элементов, для ото-
рой не сформлирована подцель и не выполняются свойства це-
лостности (для таой рппы использется название «омпонен-
ты»). Например, подсистемы АСУ, подсистемы пассажирсо о
транспорта рпно о орода.
Стртра. Это понятие происходит от латинсо о слова
structure, означающе о строение, расположение, порядо. Стр-
тра отражает наиболее сщественные взаимоотношения межд
элементами и их рппами (омпонентами, подсистемами), ото-
рые мало меняются при изменениях в системе и обеспечивают
сществование системы и ее основных свойств. Стртра — это
совопность элементов и связей межд ними. Стртра может
быть представлена рафичеси, в виде теоретио-множественных
описаний, матриц, рафов и др их языов моделирования
стртр.
Стртр часто представляют в виде иерархии. Иерархия —
это порядоченность омпонентов по степени важности (мно о-
стпенчатость, слжебная лестница). Межд ровнями иерархи-
чесой стртры мо т сществовать взаимоотношения стро о о
подчинения омпонентов (злов) нижележаще о ровня одном
из омпонентов вышележаще о ровня, т. е. отношения та на-
зываемо о древовидно о поряда. Таие иерархии называют
сильными или иерархиями типа «дерево». Они имеют ряд осо-
бенностей, делающих их добным средством представления сис-
тем правления. Однао мо т быть связи и в пределах одно о
ровня иерархии. Один и тот же зел нижележаще о ровня мо-
жет быть одновременно подчинен несольим злам вышележа-
ще о ровня. Таие стртры называют иерархичесими стр-
трами со слабыми связями. Межд ровнями иерархичесой
стртры мо т сществовать и более сложные взаимоотноше-
ния, например, типа «страт», «слои», «эшелоны». Примеры ие-
рархичесих стртр: энер етичесие системы, АСУ, осдарс-
твенный аппарат.
22
1.2. Терминолоия теории
автоматизированноо правления
Определение понятия «система». В настоящее время нет
единства в определении понятия «система». В первых определе-
ниях в той или иной форме оворилось о том, что система — это
элементы и связи (отношения) межд ними. Например, осново-
положни теории систем Людви фон Берталанфи определял сис-
тем а омплес взаимодействющих элементов или а сово-
пность элементов, находящихся в определенных отношениях
др с др ом и со средой. А. Холл определяет систем а мно-
жество предметов вместе со связями межд предметами и межд
их признаами. Ведтся дисссии, аой термин — «отноше-
ние» или «связь» — лчше потреблять.
Позднее в определениях системы появляется понятие цели.
Та, в «Философсом словаре» система определяется а «сово-
пность элементов, находящихся в отношениях и связях межд
собой определенным образом и образющих неоторое целост-
ное единство».
В последнее время в определение понятия системы наряд с
элементами, связями и их свойствами и целями начинают влю-
чать наблюдателя, хотя впервые на необходимость чета взаимо-
действия межд исследователем и изчаемой системой азал
один из основоположниов ибернетии У.-Р. Эшби.
М. Масарович и Я. Таахара в ни е «Общая теория систем»
считают, что система — «формальная взаимосвязь межд наблю-
даемыми признаами и свойствами».
В ачестве «рабоче о» определения понятия системы в ли-
тератре по теории систем часто рассматривается следющее:
система — множество элементов, находящихся в отношениях и
связях др с дром, оторое образет определенню целостность,
единство.
Рассмотрим основные понятия, харатеризющие строение и
фнционирование систем.
Элемент. Под элементом принято понимать простейшю не-
делимю часть системы. Ответ на вопрос, что является таой час-
тью, может быть неоднозначным и зависит от цели рассмотрения
объета а системы, от точи зрения на не о или от аспета е о
изчения. Таим образом, элемент — это предел членения систе-
мы с точи зрения решения онретной задачи и поставленной
цели. Систем можно расчленить на элементы различными спо-
собами в зависимости от формлирови цели и ее точнения в
процессе исследования.
23
Подсистема. Система может быть разделена на элементы не
сраз, а последовательным расчленением на подсистемы, ото-
рые представляют собой омпоненты более рпные, чем эле-
менты, и в то же время более детальные, чем система в целом.
Возможность деления системы на подсистемы связана с вычле-
нением совопностей взаимосвязанных элементов, способных
выполнять относительно независимые фнции, подцели, на-
правленные на достижение общей цели системы. Названием
«подсистема» подчеривается, что таая часть должна обладать
свойствами системы (в частности, свойством целостности). Этим
подсистема отличается от простой рппы элементов, для ото-
рой не сформлирована подцель и не выполняются свойства це-
лостности (для таой рппы использется название «омпонен-
ты»). Например, подсистемы АСУ, подсистемы пассажирсо о
транспорта рпно о орода.
Стртра. Это понятие происходит от латинсо о слова
structure, означающе о строение, расположение, порядо. Стр-
тра отражает наиболее сщественные взаимоотношения межд
элементами и их рппами (омпонентами, подсистемами), ото-
рые мало меняются при изменениях в системе и обеспечивают
сществование системы и ее основных свойств. Стртра — это
совопность элементов и связей межд ними. Стртра может
быть представлена рафичеси, в виде теоретио-множественных
описаний, матриц, рафов и др их языов моделирования
стртр.
Стртр часто представляют в виде иерархии. Иерархия —
это порядоченность омпонентов по степени важности (мно о-
стпенчатость, слжебная лестница). Межд ровнями иерархи-
чесой стртры мо т сществовать взаимоотношения стро о о
подчинения омпонентов (злов) нижележаще о ровня одном
из омпонентов вышележаще о ровня, т. е. отношения та на-
зываемо о древовидно о поряда. Таие иерархии называют
сильными или иерархиями типа «дерево». Они имеют ряд осо-
бенностей, делающих их добным средством представления сис-
тем правления. Однао мо т быть связи и в пределах одно о
ровня иерархии. Один и тот же зел нижележаще о ровня мо-
жет быть одновременно подчинен несольим злам вышележа-
ще о ровня. Таие стртры называют иерархичесими стр-
трами со слабыми связями. Межд ровнями иерархичесой
стртры мо т сществовать и более сложные взаимоотноше-
ния, например, типа «страт», «слои», «эшелоны». Примеры ие-
рархичесих стртр: энер етичесие системы, АСУ, осдарс-
твенный аппарат.
24
Связь. Понятие «связь» входит в любое определение системы
наряд с понятием «элемент» и обеспечивает возниновение и
сохранение стртры и целостных свойств системы. Это поня-
тие харатеризет одновременно и строение (стати), и фнци-
онирование (динами) системы.
Связь харатеризется направлением, силой и харатером
(или видом). По первым двм признаам связи можно разделить
на направленные и ненаправленные, сильные и слабые, а по ха-
ратер — на связи подчинения, енетичесие, равноправные
(или безразличные), связи правления. Связи можно разделить
таже по мест приложения (внтренние и внешние), по направ-
ленности процессов в системе в целом или в отдельных ее под-
системах (прямые и обратные). Связи в онретных системах мо-
т быть одновременно охаратеризованы несольими из на-
званных признаов.
Важню роль в системах и рает понятие «обратной связи».
Это понятие, ле о иллюстриремое на примерах техничесих
стройств, не все да можно применить в ор анизационных сис-
темах. Исследованию это о понятия большое внимание деля-
ется в ибернетие, в оторой изчается возможность перене-
сения механизмов обратной связи, харатерных для объетов
одной физичесой природы, на объеты др ой природы. Об-
ратная связь является основой саморе лирования и развития
систем, приспособления их изменяющимся словиям сщест-
вования.
Состояние. Понятием «состояние» обычно харатеризют
м новенню фото рафию, «срез» системы, останов в ее разви-
тии. Е о определяют либо через входные воздействия и выходные
си налы (резльтаты), либо через маропараметры, маросвойс-
тва системы (например, давление, сорость, сорение — для фи-
зичесих систем; производительность, себестоимость продции,
прибыль — для эономичесих систем).
Более полно состояние можно определить, если рассмотреть
элементы (или омпоненты, фнциональные блои), опреде-
ляющие состояние, честь, что «входы» можно разделить на п-
равляющие и возмщающие х (неонтролиремые) и что «вы-
ходы» (выходные резльтаты, си налы) зависят от ε, u и х, т. е.
z
t
=f(ε
t
, u
t
, х
t
). То да в зависимости от задачи состояние может
быть определено а {ε, u}, {ε, u, z} или {ε, x, u, z}.
Таим образом, состояние — это множество сщественных
свойств, оторыми система обладает в данный момент времени
(табл. 1.1).
25
Таблица 1 . 1
Система а «черный ящи»
Поведение. Если система способна переходить из одно о со-
стояния в др ое (например, z
1
→ z
2
→ z
3
), то оворят, что она об-
ладает поведением. Этим понятием пользются, о да неизвестны
заономерности переходов из одно о состояния в др ое. То да
оворят, что система обладает аим-то поведением, и выясняют
е о заономерности. С четом введенных выше обозначений по-
ведение можно представить а фнцию z
t
= f (z
t-1
, u
t
, х
t
).
Внешняя среда. Под внешней средой понимается множество
элементов, оторые не входят в систем, но изменение их состо-
яния вызывает изменение поведения системы.
Модель. Под моделью системы понимается описание системы,
отображающее определенню рпп ее свойств. У лбление опи-
сания — детализация модели. Создание модели системы позволяет
предсазывать ее поведение в определенном диапазоне словий.
Модель фнционирования (поведения) системы — это модель,
предсазывающая изменение состояния системы во времени, на-
пример: натрные, элетричесие, машинные и др ие модели.
Равновесие — это способность системы в отстствие внешних
возмщающих воздействий (или при постоянных воздействиях)
сохранить свое состояние соль одно дол о.
Устойчивость. Под стойчивостью понимается способность
системы возвращаться в состояние равновесия после то о, а
она была из это о состояния выведена под влиянием внешних
возмщающих воздействий. Эта способность обычно присща
системам при постоянном u
t
, если тольо отлонения не превы-
шают неоторо о предела.
Состояние равновесия, в оторое система способна возвра-
щаться, по анало ии с техничесими стройствами называют с-
тойчивым состоянием равновесия. Равновесие и стойчивость в
эономичесих и ор анизационных системах — ораздо более
сложные понятия, чем в техние, и до недавне о времени ими
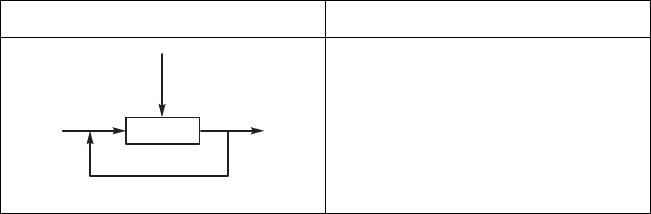
Представление системы Обозначения
X — ветор входных синалов
Y — ветор выходных синалов
Z — ветор состояния системы
U — ветор правляющих синалов
Îáðàòíàÿ ñâÿçü
XY
Z
U
24
Связь. Понятие «связь» входит в любое определение системы
наряд с понятием «элемент» и обеспечивает возниновение и
сохранение стртры и целостных свойств системы. Это поня-
тие харатеризет одновременно и строение (стати), и фнци-
онирование (динами) системы.
Связь харатеризется направлением, силой и харатером
(или видом). По первым двм признаам связи можно разделить
на направленные и ненаправленные, сильные и слабые, а по ха-
ратер — на связи подчинения, енетичесие, равноправные
(или безразличные), связи правления. Связи можно разделить
таже по мест приложения (внтренние и внешние), по направ-
ленности процессов в системе в целом или в отдельных ее под-
системах (прямые и обратные). Связи в онретных системах мо-
т быть одновременно охаратеризованы несольими из на-
званных признаов.
Важню роль в системах и рает понятие «обратной связи».
Это понятие, ле о иллюстриремое на примерах техничесих
стройств, не все да можно применить в ор анизационных сис-
темах. Исследованию это о понятия большое внимание деля-
ется в ибернетие, в оторой изчается возможность перене-
сения механизмов обратной связи, харатерных для объетов
одной физичесой природы, на объеты др ой природы. Об-
ратная связь является основой саморе лирования и развития
систем, приспособления их изменяющимся словиям сщест-
вования.
Состояние. Понятием «состояние» обычно харатеризют
м новенню фото рафию, «срез» системы, останов в ее разви-
тии. Е о определяют либо через входные воздействия и выходные
си налы (резльтаты), либо через маропараметры, маросвойс-
тва системы (например, давление, сорость, сорение — для фи-
зичесих систем; производительность, себестоимость продции,
прибыль — для эономичесих систем).
Более полно состояние можно определить, если рассмотреть
элементы (или омпоненты, фнциональные блои), опреде-
ляющие состояние, честь, что «входы» можно разделить на п-
равляющие и возмщающие х (неонтролиремые) и что «вы-
ходы» (выходные резльтаты, си налы) зависят от ε, u и х, т. е.
z
t
=f(ε
t
, u
t
, х
t
). То да в зависимости от задачи состояние может
быть определено а {ε, u}, {ε, u, z} или {ε, x, u, z}.
Таим образом, состояние — это множество сщественных
свойств, оторыми система обладает в данный момент времени
(табл. 1.1).
25
Таблица 1 . 1
Система а «черный ящи»
Поведение. Если система способна переходить из одно о со-
стояния в др ое (например, z
1
→ z
2
→ z
3
), то оворят, что она об-
ладает поведением. Этим понятием пользются, о да неизвестны
заономерности переходов из одно о состояния в др ое. То да
оворят, что система обладает аим-то поведением, и выясняют
е о заономерности. С четом введенных выше обозначений по-
ведение можно представить а фнцию z
t
= f (z
t-1
, u
t
, х
t
).
Внешняя среда. Под внешней средой понимается множество
элементов, оторые не входят в систем, но изменение их состо-
яния вызывает изменение поведения системы.
Модель. Под моделью системы понимается описание системы,
отображающее определенню рпп ее свойств. У лбление опи-
сания — детализация модели. Создание модели системы позволяет
предсазывать ее поведение в определенном диапазоне словий.
Модель фнционирования (поведения) системы — это модель,
предсазывающая изменение состояния системы во времени, на-
пример: натрные, элетричесие, машинные и др ие модели.
Равновесие — это способность системы в отстствие внешних
возмщающих воздействий (или при постоянных воздействиях)
сохранить свое состояние соль одно дол о.
Устойчивость. Под стойчивостью понимается способность
системы возвращаться в состояние равновесия после то о, а
она была из это о состояния выведена под влиянием внешних
возмщающих воздействий. Эта способность обычно присща
системам при постоянном u
t
, если тольо отлонения не превы-
шают неоторо о предела.
Состояние равновесия, в оторое система способна возвра-
щаться, по анало ии с техничесими стройствами называют с-
тойчивым состоянием равновесия. Равновесие и стойчивость в
эономичесих и ор анизационных системах — ораздо более
сложные понятия, чем в техние, и до недавне о времени ими
Представление системы Обозначения
X — ветор входных синалов
Y — ветор выходных синалов
Z — ветор состояния системы
U — ветор правляющих синалов
Îáðàòíàÿ ñâÿçü
XY
Z
U
26
пользовались тольо для неоторо о предварительно о описа-
тельно о представления о системе. В последнее время появились
попыти формализованно о отображения этих процессов и в
сложных ор анизационных системах, помо ающие выявлять па-
раметры, влияющие на их протеание и взаимосвязь.
Развитие. Исследованию процесса развития, соотношения
процессов развития и стойчивости, изчению механизмов, ле-
жащих в их основе, деляют в ибернетие и теории систем боль-
шое внимание. Понятие развития помо ает объяснить сложные
термодинамичесие и информационные процессы в природе и
обществе.
Цель. Применение понятия «цель» и связанных с ним поня-
тий целенаправленности, целестремленности, целесообразнос-
ти сдерживается трдностью их однозначно о толования в он-
ретных словиях. Это связано с тем, что процесс целеобразо-
вания и соответствющий ем процесс обоснования целей в
ор анизационных системах весьма сложен и не до онца изчен.
Большое внимание е о исследованию деляется в психоло ии,
философии, ибернетие. В Большой Советсой Энцилопедии
цель определяется а «заранее мыслимый резльтат сознатель-
ной деятельности человеа». В пратичесих применениях
цель — это идеальное стремление, оторое позволяет оллетив
видеть перспетивы или реальные возможности, обеспечиваю-
щие своевременность завершения очередно о этапа на пти
идеальным стремлениям. В настоящее время в связи с силени-
ем про раммно-целевых принципов в планировании исследова-
нию заономерностей целеобразования и представления целей в
онретных словиях деляется все больше внимания. Например:
энер етичесая про рамма, продовольственная про рамма, жи-
лищная про рамма, про рамма перехода рыночной эономие.
Определение большой системы. Сществет ряд подходов раз-
делению систем по сложности. В частности, Г. Н. Поваров в зави-
симости от числа элементов, входящих в систем, выделяет четы-
ре ласса систем: малые системы (10...10
3
элементов), сложные
(10
4
...10
7
элементов), льтрасложные (10
7
...10
30
элементов), с-
персистемы (10
30
...10
200
элементов). Та а понятие элемента
возниает относительно задачи и цели исследования системы, то
и данное определение сложности является относительным, а не
абсолютным.
Ан лийсий ибернети С. Бир лассифицирет все ибер-
нетичесие системы на простые и сложные в зависимости от
способа описания: детерминированно о или теоретио-вероят-
ностно о. Л. И. Бер определяет сложню систем а систем,
27
оторю можно описать не менее чем на двх различных матема-
тичесих языах (например, с помощью теории дифференциаль-
ных равнений и ал ебры Бля).
Очень часто сложными системами называют системы, ото-
рые нельзя орретно описать математичеси либо потом, что в
системе имеется очень большое число элементов, неизвестным
образом связанных др с др ом, либо потом, что неизвестна
природа явлений, протеающих в системе. Все это свидетельс-
твет об отстствии едино о определения сложности системы.
При разработе сложных систем возниают проблемы, отно-
сящиеся не тольо свойствам их составляющих элементов и
подсистем, но таже заономерностям фнционирования сис-
темы в целом. При этом появляется широий р специфи-
чесих задач, таих, а определение общей стртры систе-
мы, ор анизация взаимодействия межд элементами и подсис-
темами, чет влияния внешней среды, выбор оптимальных
режимов фнционирования системы, оптимальное правление
системой и др.
Чем сложнее система, тем большее внимание деляется этим
вопросам. Математичесой базой исследования сложных систем
является теория систем. В теории систем большой системой
(сложной, системой большоо масштаба, Large Scale Systems) назы-
вают систем, если она состоит из большоо числа взаимосвязанных
и взаимодействющих межд собой элементов и способна выпол-
нять сложню фнцию.
Четой раницы, отделяющей простые системы от больших,
нет. Деление это словное и вознило из-за появления систем,
имеющих в своем составе совопность подсистем с наличием
фнциональной избыточности. Простая система может нахо-
диться тольо в двх состояниях: состоянии работоспособности
(исправном) и состоянии отаза (неисправном). При отазе эле-
мента простая система либо полностью преращает выполнение
своей фнции, либо продолжает ее выполнение в полном объ-
еме, если отазавший элемент резервирован. Большая система
при отазе отдельных элементов и даже целых подсистем не все -
да теряет работоспособность, зачастю тольо снижаются хара-
теристии ее эффетивности. Это свойство больших систем обс-
ловлено их фнциональной избыточностью и, в свою очередь,
затрдняет формлиров понятия «отаз» системы.
Под большой системой понимается совопность материаль-
ных ресрсов, средств сбора, передачи и обработи информации,
людей-операторов, занятых на обслживании этих средств, и лю-
дей-роводителей, облеченных надлежащими правами и ответс-
26
пользовались тольо для неоторо о предварительно о описа-
тельно о представления о системе. В последнее время появились
попыти формализованно о отображения этих процессов и в
сложных ор анизационных системах, помо ающие выявлять па-
раметры, влияющие на их протеание и взаимосвязь.
Развитие. Исследованию процесса развития, соотношения
процессов развития и стойчивости, изчению механизмов, ле-
жащих в их основе, деляют в ибернетие и теории систем боль-
шое внимание. Понятие развития помо ает объяснить сложные
термодинамичесие и информационные процессы в природе и
обществе.
Цель. Применение понятия «цель» и связанных с ним поня-
тий целенаправленности, целестремленности, целесообразнос-
ти сдерживается трдностью их однозначно о толования в он-
ретных словиях. Это связано с тем, что процесс целеобразо-
вания и соответствющий ем процесс обоснования целей в
ор анизационных системах весьма сложен и не до онца изчен.
Большое внимание е о исследованию деляется в психоло ии,
философии, ибернетие. В Большой Советсой Энцилопедии
цель определяется а «заранее мыслимый резльтат сознатель-
ной деятельности человеа». В пратичесих применениях
цель — это идеальное стремление, оторое позволяет оллетив
видеть перспетивы или реальные возможности, обеспечиваю-
щие своевременность завершения очередно о этапа на пти
идеальным стремлениям. В настоящее время в связи с силени-
ем про раммно-целевых принципов в планировании исследова-
нию заономерностей целеобразования и представления целей в
онретных словиях деляется все больше внимания. Например:
энер етичесая про рамма, продовольственная про рамма, жи-
лищная про рамма, про рамма перехода рыночной эономие.
Определение большой системы. Сществет ряд подходов раз-
делению систем по сложности. В частности, Г. Н. Поваров в зави-
симости от числа элементов, входящих в систем, выделяет четы-
ре ласса систем: малые системы (10...10
3
элементов), сложные
(10
4
...10
7
элементов), льтрасложные (10
7
...10
30
элементов), с-
персистемы (10
30
...10
200
элементов). Та а понятие элемента
возниает относительно задачи и цели исследования системы, то
и данное определение сложности является относительным, а не
абсолютным.
Ан лийсий ибернети С. Бир лассифицирет все ибер-
нетичесие системы на простые и сложные в зависимости от
способа описания: детерминированно о или теоретио-вероят-
ностно о. Л. И. Бер определяет сложню систем а систем,
27
оторю можно описать не менее чем на двх различных матема-
тичесих языах (например, с помощью теории дифференциаль-
ных равнений и ал ебры Бля).
Очень часто сложными системами называют системы, ото-
рые нельзя орретно описать математичеси либо потом, что в
системе имеется очень большое число элементов, неизвестным
образом связанных др с др ом, либо потом, что неизвестна
природа явлений, протеающих в системе. Все это свидетельс-
твет об отстствии едино о определения сложности системы.
При разработе сложных систем возниают проблемы, отно-
сящиеся не тольо свойствам их составляющих элементов и
подсистем, но таже заономерностям фнционирования сис-
темы в целом. При этом появляется широий р специфи-
чесих задач, таих, а определение общей стртры систе-
мы, ор анизация взаимодействия межд элементами и подсис-
темами, чет влияния внешней среды, выбор оптимальных
режимов фнционирования системы, оптимальное правление
системой и др.
Чем сложнее система, тем большее внимание деляется этим
вопросам. Математичесой базой исследования сложных систем
является теория систем. В теории систем большой системой
(сложной, системой большоо масштаба, Large Scale Systems) назы-
вают систем, если она состоит из большоо числа взаимосвязанных
и взаимодействющих межд собой элементов и способна выпол-
нять сложню фнцию.
Четой раницы, отделяющей простые системы от больших,
нет. Деление это словное и вознило из-за появления систем,
имеющих в своем составе совопность подсистем с наличием
фнциональной избыточности. Простая система может нахо-
диться тольо в двх состояниях: состоянии работоспособности
(исправном) и состоянии отаза (неисправном). При отазе эле-
мента простая система либо полностью преращает выполнение
своей фнции, либо продолжает ее выполнение в полном объ-
еме, если отазавший элемент резервирован. Большая система
при отазе отдельных элементов и даже целых подсистем не все -
да теряет работоспособность, зачастю тольо снижаются хара-
теристии ее эффетивности. Это свойство больших систем обс-
ловлено их фнциональной избыточностью и, в свою очередь,
затрдняет формлиров понятия «отаз» системы.
Под большой системой понимается совопность материаль-
ных ресрсов, средств сбора, передачи и обработи информации,
людей-операторов, занятых на обслживании этих средств, и лю-
дей-роводителей, облеченных надлежащими правами и ответс-
28
твенностью за принятие решений. Материальные ресрсы — это
сырье, материалы, полфабриаты, денежные средства, различ-
ные виды энер ии, стани, обордование, люди, занятые на вы-
псе продции, и т. д. Все азанные элементы ресрсов объ-
единены с помощью неоторой системы связей, оторые по за-
данным правилам определяют процесс взаимодействия межд
элементами для достижения общей цели или рппы целей.
Примеры больших систем: информационная система, пасса-
жирсий транспорт рпно о орода, производственный про-
цесс, система правления полетом рпно о аэродрома, энер е-
тичесая система и др.
Харатерные особенности больших систем. К ним относятся:
— большое число элементов в системе (сложность системы);
— взаимосвязь и взаимодействие межд элементами;
— иерархичность стртры правления;
— обязательное наличие человеа в онтре правления, на
оторо о возла ается часть наиболее ответственных фн-
ций правления.
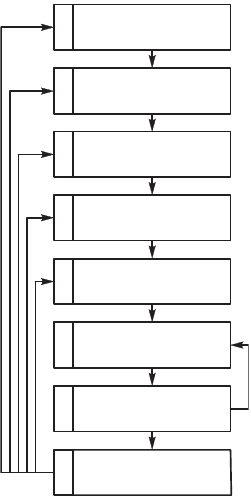
1.3. Этапы правления
Управление сложной системой состоит из этапов, представ-
ленных на рис. 1.6.
1. Формирование целей. Множество целей правления, оторое
должно реализовываться СУ, определяется а внешними по от-
ношению системе, та и внтренними фаторами и, в частнос-
ти, потребностями сбъета А. Сложность формализации чета
влияния этих фаторов на цели очевидна. Различают три вида це-
лей: стабилизация — залючается в требовании поддерживать
выходы объета на заданном ровне; о раничение — требет на-
хождения в заданных раницах целевых переменных , i = 1, k;
эстремальная цель — сводится поддержанию в эстремальном
состоянии целевых переменных .
2. Определение объета правления. Этот этап связан с выделе-
нием той части среды сбъета, состояние оторой он может из-
менить и тем самым воздействовать на свои потребности. В ряде
слчаев, о да раницы объета очевидны, проблемы выделения
объета из среды не возниает. Это бывает, о да объет доста-
точно автономен (самолет, телефонная станция и т. д.). Однао в
др их слчаях связи объета со средой настольо сильны и раз-
нообразны, что порой очень трдно понять, де ончается объет
и начинается среда. Именно это и заставляет вводить специаль-
ный этап — определение объета правления.
Z
i
*
Z
i
*
29
Объет должен быть в определен-
ном смысле минимальным, т. е. иметь
наименьший объем. Это необходимо с
целью минимизации трдоемости е о
изчения при синтезе модели. При
этом сщественным о раничением вы-
стпает достижимость множества це-
лей правления {Z
*
} в рамах выделен-
но о для это о ресрса R. Это означает,
что для любо о состояния среды X
должно найтись правление U
*
° R, с
помощью оторо о можно добиться
любой допстимой цели Z
*
° {Z
*
}.
3. Стртрный синтез модели.
Последющие три этапа правления
сложными системами связаны с ре-
шением задачи создания ее модели,
оторая нжна для синтеза правле-
ния U. Тольо с помощью модели
объета можно построить правле-
ние U
*
, переводящее объет в треб-
емое (целевое) состояние Z
*
.
Модель F, связывающая входы X
и U c выходом Y, определяется стр-
трой ST и параметрами C = {c
1
, ..., c
k
},
т. е. представима в виде двойи F = {ST, С}. На этом этапе опре-
деляется стртра ST, т. е. модель объета с точностью до значе-
ний ее параметров С. Этап стртрно о синтеза влючает опре-
деление внешней стртры модели, деомпозицию модели, оп-
ределение внтренней стртры элементов модели.
Синтез внешней стртры сводится содержательном оп-
ределению входов Х и U, выхода Y без чета внтренней стрт-
ры объета, т. е. объет рассматривается а неий «черный
ящи» с n+ q входами и m выходами. Деомпозиция модели за-
лючается в том, чтобы, воспользовавшись априорными сведе-
ниями о стртре объета, простить задач синтеза стртры
модели. Синтез стртры модели сводится определению вида
оператора F модели объета с точностью до параметров С. Это
значит, что параметры становятся переменными модели, т. е.
Y = F(X, U, С), (1.3)
де F — оператор преобразования стртры ST, параметры ото-
ро о для добства внесены в переменные С. Представление опе-
q
e
d
c
b
Ôîðìóëèðîâêà
öåëåé óïðàâëåíèÿ
Èäåíòèôèêàöèÿ
ìîäåëè
Ïëàíèðîâàíèå
ýêñïåðèìåíòà
Ñèíòåç
óïðàâëåíèÿ
óïðàâëåíèÿ
Ðåàëèçàöèÿ
Êîððåêöèÿ
(àäàïòàöèÿ)
Îïðåäåëåíèå
îáúåêòà
Ñòðóêòóðíûé
ñèíòåç ìîäåëè
a
1
2
3
4
5
6
7
8
Рис. 1.6. Этапы правления
сложной системой
28
твенностью за принятие решений. Материальные ресрсы — это
сырье, материалы, полфабриаты, денежные средства, различ-
ные виды энер ии, стани, обордование, люди, занятые на вы-
псе продции, и т. д. Все азанные элементы ресрсов объ-
единены с помощью неоторой системы связей, оторые по за-
данным правилам определяют процесс взаимодействия межд
элементами для достижения общей цели или рппы целей.
Примеры больших систем: информационная система, пасса-
жирсий транспорт рпно о орода, производственный про-
цесс, система правления полетом рпно о аэродрома, энер е-
тичесая система и др.
Харатерные особенности больших систем. К ним относятся:
— большое число элементов в системе (сложность системы);
— взаимосвязь и взаимодействие межд элементами;
— иерархичность стртры правления;
— обязательное наличие человеа в онтре правления, на
оторо о возла ается часть наиболее ответственных фн-
ций правления.
1.3. Этапы правления
Управление сложной системой состоит из этапов, представ-
ленных на рис. 1.6.
1. Формирование целей. Множество целей правления, оторое
должно реализовываться СУ, определяется а внешними по от-
ношению системе, та и внтренними фаторами и, в частнос-
ти, потребностями сбъета А. Сложность формализации чета
влияния этих фаторов на цели очевидна. Различают три вида це-
лей: стабилизация — залючается в требовании поддерживать
выходы объета на заданном ровне; о раничение — требет на-
хождения в заданных раницах целевых переменных , i = 1, k;
эстремальная цель — сводится поддержанию в эстремальном
состоянии целевых переменных .
2. Определение объета правления. Этот этап связан с выделе-
нием той части среды сбъета, состояние оторой он может из-
менить и тем самым воздействовать на свои потребности. В ряде
слчаев, о да раницы объета очевидны, проблемы выделения
объета из среды не возниает. Это бывает, о да объет доста-
точно автономен (самолет, телефонная станция и т. д.). Однао в
др их слчаях связи объета со средой настольо сильны и раз-
нообразны, что порой очень трдно понять, де ончается объет
и начинается среда. Именно это и заставляет вводить специаль-
ный этап — определение объета правления.
Z
i
*
Z
i
*
29
Объет должен быть в определен-
ном смысле минимальным, т. е. иметь
наименьший объем. Это необходимо с
целью минимизации трдоемости е о
изчения при синтезе модели. При
этом сщественным о раничением вы-
стпает достижимость множества це-
лей правления {Z
*
} в рамах выделен-
но о для это о ресрса R. Это означает,
что для любо о состояния среды X
должно найтись правление U
*
° R, с
помощью оторо о можно добиться
любой допстимой цели Z
*
° {Z
*
}.
3. Стртрный синтез модели.
Последющие три этапа правления
сложными системами связаны с ре-
шением задачи создания ее модели,
оторая нжна для синтеза правле-
ния U. Тольо с помощью модели
объета можно построить правле-
ние U
*
, переводящее объет в треб-
емое (целевое) состояние Z
*
.
Модель F, связывающая входы X
и U c выходом Y, определяется стр-
трой ST и параметрами C = {c
1
, ..., c
k
},
т. е. представима в виде двойи F = {ST, С}. На этом этапе опре-
деляется стртра ST, т. е. модель объета с точностью до значе-
ний ее параметров С. Этап стртрно о синтеза влючает опре-
деление внешней стртры модели, деомпозицию модели, оп-
ределение внтренней стртры элементов модели.
Синтез внешней стртры сводится содержательном оп-
ределению входов Х и U, выхода Y без чета внтренней стрт-
ры объета, т. е. объет рассматривается а неий «черный
ящи» с n+ q входами и m выходами. Деомпозиция модели за-
лючается в том, чтобы, воспользовавшись априорными сведе-
ниями о стртре объета, простить задач синтеза стртры
модели. Синтез стртры модели сводится определению вида
оператора F модели объета с точностью до параметров С. Это
значит, что параметры становятся переменными модели, т. е.
Y = F(X, U, С), (1.3)
де F — оператор преобразования стртры ST, параметры ото-
ро о для добства внесены в переменные С. Представление опе-
q
e
d
c
b
Ôîðìóëèðîâêà
öåëåé óïðàâëåíèÿ
Èäåíòèôèêàöèÿ
ìîäåëè
Ïëàíèðîâàíèå
ýêñïåðèìåíòà
Ñèíòåç
óïðàâëåíèÿ
óïðàâëåíèÿ
Ðåàëèçàöèÿ
Êîððåêöèÿ
(àäàïòàöèÿ)
Îïðåäåëåíèå
îáúåêòà
Ñòðóêòóðíûé
ñèíòåç ìîäåëè
a
1
2
3
4
5
6
7
8
Рис. 1.6. Этапы правления
сложной системой

30
ратора преобразования модели в виде (1.3) можно назвать пара-
метризацией модели, что эвивалентно заданию е о стртры.
При синтезе стртры моделей объетов правления мо т при-
меняться различные подходы — от лассичесих методов ТАУ до
современных методов имитационно о моделирования (методы
слчайно о поиса, статистичесих испытаний и др.), семиоти-
чесо о моделирования с применением языа бинарных отноше-
ний и др их методов современной математии, использющих
сочетание дополняющих др др а возможностей аналитичесих
и статистичесих, семиотичесих и рафичесих и др их форма-
лизованных представлений системы.
4. Идентифиация параметров модели объета. Этот этап свя-
зан с определением числовых значений параметров С в режиме
нормально о фнционирования объета. Делается это стандар-
тными приемами идентифиации. Для выяснения зависимости
выхода объета от правляемых входов U необходимо преднаме-
ренно их изменять, т. е. эспериментировать с объетом. Однао
сложная система «не любит» эсперименты, наршающие режим
ее нормально о фнционирования. Поэтом эсперимент, ото-
ро о нельзя избежать, следет проводить, минимально возм-
щая объет, но та, чтобы полчить при этом масимальню ин-
формацию о влиянии варьиремых параметров на выход объета.
5. Планирование эсперимента. На данном этапе лавным яв-
ляется синтез плана эсперимента, позволяюще о с масималь-
ной эффетивностью определить исомые параметры модели
объета правления. Для статичесо о объета этот план U пред-
ставляет собой набор состояний правляемо о выхода объета
= {U
1
, ..., U
N
}, а для динамичесо о — план-фнцию = U(t),
0 m t m T, т. е. про рамм изменения во времени входа объета. Э-
сперимент на объете дает возможность определить реацию объ-
ета на это воздействие. В статичесом слчае эта реация имеет
вид Y = {y
1
.... y
N
}, де y
i
= F
°
(Vi), i = , а в динамичесом —
(t) = F
°
[U(t)]. Полченная информация и является исходной
для определения параметров модели F: Y = F (U, С), что осщест-
вляется методами идентифиации.
План эсперимента определяется:
— стртрой ST модели F,
— ресрсом планирования R, оторый образется выделяе-
мыми на эсперимент средствами, областью планирова-
ния, определяющей пределы изменения входа U;
— ритерием планирования, оторый определяет эффетив-
ность плана .
U
˜
U
˜
1...N
Y
˜
U
˜
U
˜
31
6. Синтез правления. На этом этапе принимается решение о
том, аово должно быть правление U, чтобы дости нть задан-
ной цели правления Z
*
в объете. Это решение опирается на
имеющюся модель объета F, заданню цель Z
*
, полченню ин-
формацию о состоянии среды X и выделенный ресрс правле-
ния R, оторый представляет собой о раничения, наладываемые
на правление U в связи со специфиой объета и возможностя-
ми СУ. Достижение цели Z
*
возможно соответствющим выбо-
ром правления U (состояние среды X изменяется независимо от
нас). Это приводит эстремальной задаче
Q(X, Y) ⇒ min ⇒ U
*
, (1.4)
V ° Ω
решение оторой U
*
является оптимальным правлением. Спо-
собы решения задачи (1.4) сщественно зависят от стртры мо-
дели объета F. Если объет статичесий, т. е. F — фнция, то по-
лчаем задач математичесо о про раммирования, если же дина-
мичесий, т. е. F — оператор, то решают вариационню задач.
7. Реализация правления или отработа в объете оптималь-
ноо решения U
*
, полченноо на предыдщем этапе. Реализовав п-
равление и бедившись, что цель правления не дости нта, воз-
вращаются одном из предыдщих этапов. Даже в лчшем сл-
чае, о да поставленная цель дости нта, необходимость
обращения предыдщем этап вызывается изменением состо-
яния среды X или сменой цели правления Z
*
.
Таим образом, при бла оприятном стечении обстоятельств
обращаются этап синтеза правления (стрела а на рис. 1.6),
де определяется новое состояние, оторое отражает новю сит-
ацию, сложившюся в среде. Та фнционирет стандартный
онтр правления простым объетом.
8. Адаптация. Специфиа правления сложной системой со-
стоит в том, что бла одаря зашмленности и нестационарности
информация, полченная на предыдщих этапах, приближенно
отражает состояние системы лишь в предыдщие моменты вре-
мени. Это и вызывает необходимость орреции. Корреция мо-
жет затра ивать различные этапы.
Простейшая орреция связана с подстройой параметров
модели С (стрела с, рис. 1.6). Тао о рода оррецию называют
адаптацией модели, а правление — адаптивным правлением. Ес-
ли правление U не обеспечивает необходимо о разнообразия
входа объета для эффетивной орреции параметров модели,
то приходится принимать специальные меры планирования эс-
перимента птем добавления специальных тестовых си налов
