Menke W. Geophysical Data Analysis: Discrete Inverse Theory
Подождите немного. Документ загружается.


58
3
Linear, Gaussian Inverse
Problem,
Viewpoint
1
3.1
1
The Variance
of
the Model Parameter
Estimates
The data invariably contain noise that cause errors in the estimates
of the model parameters. We can calculate how this measurement
error "maps into" errors in
mest
by noting that all of the formulas
,
derived above for estimates of the model parameters are linear func-
tions of the data, of the form
mest
=
Md
+
v,
where
M
is some matrix
and
v
some vector. Therefore, if we assume that the data have a
distribution characterized by some covariance matrix [cov
d],
the
estimates of the model parameters have a distribution characterized by
a covariance matrix [cov
m]
=
M[cov
d]MT.
The covariance
of
the
solution can therefore be calculated in a straightforward fashion. If the
data are uncorrelated and all of equal variance
02,
then very simple
formulas are obtained for the covariance of some of the more simple
inverse problem solutions.
The simple least squares solution
mest
=
[GTG]-'GTd
has covar-
iance
[cov
m]
=
[[GTG]-'GT]a$I[[GTG]-lGT]T
=
a3GTG]-'
(3.48)
and the simple minimum length solution
mest
=
GT[GGT]-'d
has
covariance
[cov
m]
=
[GTIGGT]-l]a$IIGTIGGT]-l]T
=
a$GT[GGT]-*G
(3.49)
3.12
Variance and Prediction Error
of
the
Least Squares Solution
If
the prediction error
E(m)
=
eTe
of an overdetermined problem
has a very sharp minimum in the vicinity of the estimated solution
mest,
we would expect that the solution is well determined in the sense
that it has small variance. Small errors in determining the shape of
E(m)
due to random fluctuations in the data lead to only small errors
in
mest
(Fig. 3.1Oa). Conversely, if
E(m)
has a broad minimum, we
expect that
mest
has a large variance (Fig.
3.
lob). Since the curvature of
a function is a measure of the sharpness
of
its minimum, we expect
that the variance of the solution is related to the curvature of
E(m)
at

3.12
Variance and Prediction
Error
of
the Least Squares
Solution
59
n
E
W
v
A€
(a)
(b)
+
I'dm
rn
,,,est
model parameter
rn
n
E
W
W
A€
model
parameter
rn
Fig.
3.10.
(a) The best estimate
m"'
of
model parameter
m
occurs at the minimum
of
E(m).
If
the
minimum
is
relatively narrow, then random fluctuations
in
E(m)
lead to
only small errors
Am
in
ma'.
(b)
If
the minimum is wide, then large errors
in
m
can
occur.
its minimum. The curvature
of
the prediction error can be measured
by its second derivative, as we can see by computing how small
changes in the model parameters change the prediction error. Expand-
ing the prediction error in a Taylor series about its minimum and
keeping up to second order terms gives
AE
=
E(m)
-
E(mest)
=
[m
-
mest]T
[
1
"3
[m
-
mest]
2
am2
m-ms.t
(3.50)
Note that the first-order term is zero, since the expansion is made at a
minimum. The second derivative can also be computed directly from
the expression
E(m)
=
eTe
=
[d
-
GmIT[d
-
Gm]
which gives
(3.51)
1
"""1
-
---[d-Gmp=&[-GT[d-Gm]
I
a2
=GTG
2
am2
2
am2
The covariance
of
the least squares solution (assuming uncorrelated
data all with equal variance
CT~)
is therefore
[cov
m]
=
ai[GTC]-
(3.52)

60
3
Linear, Gaussian Inverse Problem, Viewpoint
1
The prediction error
E
=
eTe
is the sum of squares of Gaussian data
minus a constant. It is, therefore, a random variable with ax2 distribu-
tion with
N
-
Mdegrees of freedom, which has mean
(N
-
M)a2and
variance
2(N
--M)a$.(The degrees offreedom are reduced by Msince
the model can force
M
linear combinations
of
the
ei
to zero.) We can
use the standard deviation of
E,
aE
=
[2(N
-
M)]'/2a2
in the expres-
sion for variance as
[cov
m]
=
a2[GTG]-'
=
0,
[
!-
""1'
(3.53)
[2(N-
M)]1/2
2
dm2
m=mc.,
The covariance [cov
m]
can be interpreted as being controlled either by
the variance of the data times a measure of how error in the data is
mapped into error in the model parameters, or by the standard
deviation
of
the total prediction error times a measure of the curvature
of
the prediction error at its minimum.
The methods of solving inverse problems that have been discussed
in this chapter emphasize the data and model parameters themselves.
The method of least squares estimates the model parameters with
smallest prediction length. The method of minimum length estimates
the simplist model parameters. The ideas of data and model parame-
ters are very concrete and straightforward, and the methods based on
them are simple and easily understood. Nevertheless, this viewpoint
tends to obscure an important aspect of inverse problems: that the
nature of the problems depends more on the
relationship
between the
data and model parameters than on the data or model parameters
themselves. It should, for instance, be possible to tell a well-designed
experiment from a poor one without knowing what the numerical
values of the data or model parameters are, or even the range in which
they fall. In the next chapter we will begin to explore this kind
of
problem.

SOLUTION
OF
THE
LINEAR, GAUSSIAN
INVERSE PROBLEM,
VIEWPOINT
2:
GENERALIZED INVERSES
4.1
Solutions
versus Operators
In the previous chapter we derived methods of solving the linear
inverse problem
Gm
=
d
that were based on examining two properties
of its solution: prediction error and solution simplicity (or length).
Most of these solutions had a form that was linear in the data,
Md
+
v,
where
M
is some matrix and
v
some vector, both of
which are independent of the data
d.
This equation indicates that the
estimate of the model parameters is controlled by some matrix
M
operating on the data (that is, multiplying the data). We therefore shift
our emphasis from the estimates
mest
to the operator matrix
M,
with
the expectation that by studying it we can learn more about the
properties of inverse problems. Since the matrix
M
solves, or “in-
verts,” the inverse problem
Gm
=
d,
it is often called the
generalized
61
mest
=

62
4
Linear, Gaussian Inverse Problem, Viewpoint
2
inverse and gven the symbol
G-g.
The exact form of the generalized
inverse depends on the problem at hand. The generalized inverse of
the overdetermined least squares problem is
G-g
=
[GTG]-'GT,
and
for the minimum length underdetermined solution it is
G-g=
Note that in some ways the generalized inverse is analogous to the
ordinary matrix inverse. The solution to the square (even-determined)
matrix equation
Ax
=
y
is
x
=
A-'y,
and the solution to the inverse
problem
Gm
=
d
is
mest
=
G-gd
(plus some vector, possibly). The
analogy is very limited, however. The generalized inverse is not a
matrix inverse in the usual sense. It is not square, and neither
G-gG
nor
GG-g
need equal an identity matrix.
GTIGGT]-l.
4.2
The
Data Resolution Matrix
Suppose we have found a generalized inverse that in some sense
solves the inverse problem
Gm
=
d,
yielding an estimate of the model
parameters
mest
=
G-gd
(for the sake of simplicity we assume that
there is no additive vector). We can then retrospectively ask how well
this estimate of the model parameters fits the data.
By
plugging our
estimate into the equation
Gm
=
d
we conclude
(4.1)
dPre
=
Gmest
=
G[G-gdObs]
=
[GG-gIdObs
=
NdObS
Here the superscripts obs and pre mean observed and predicted,
respectively. The
N
X
N
square matrix
N
=
GG-g
is called the
data
resolution matrix. This matrix describes how well the predictions
match the data.
If
N
=
I,
then
dpre
=
dobs
and the prediction error is
zero. On the other hand, if the data resolution matrix is not an identity
matrix, the prediction error is nonzero.
If the elements of the data vector
d
possess a natural ordering, then
the data resolution matrix has a simple interpretation. Consider, for
example, the problem
of
fitting a straight line to
(z,
d)
points, where
the data have been ordered according to the value of the auxiliary
variable
z.
If
N
is not an identity matrix but is close to an identity
matrix (in the sense that its largest elements are near its main diago-
nal), then the configuration
of
the matrix signifies that averages of
neighboring data can be predicted, whereas individual data cannot.
Consider the ith row of
N.
If this row contained all zeros except for a
4.2
The
Data
Resolution
Matrix
63
one in the ith column, then
d,
would be predicted exactly. On the other
hand, suppose that the row contained the elements
[..*O
0 0
0.1
0.8
0.1
0 0
O...]
(4.2)
dye
=
c
N,,d;bs=
o.ld$;+
O.Sd?bS+
o.1dp:;
where the
0.8
is in the ith column. Then the ith datum is given by
N
(4.3)
The predicted value is a weighted average
of
three neighboring ob-
served data.
If
the true data vary slowly with the auxiliary variable,
then such an average might produce an estimate reasonably close to
the observed value.
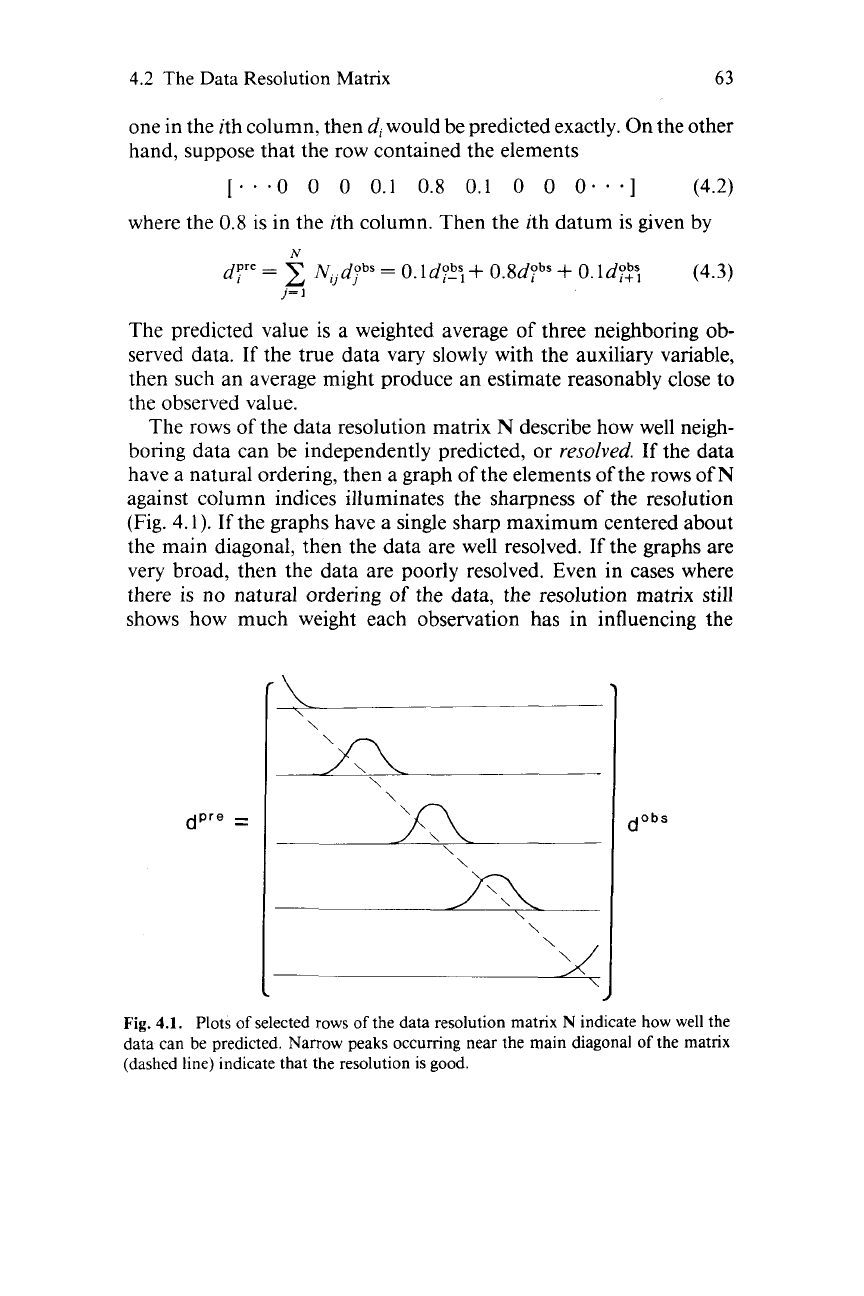
The rows
of
the data resolution matrix
N
describe how well neigh-
boring data can be independently predicted, or
resolved.
If
the data
have a natural ordering, then a graph
of
the elements
of
the rows
of
N
against column indices illuminates the sharpness
of
the resolution
(Fig. 4.1).
If
the graphs have a single sharp maximum centered about
the main diagonal, then the data are well resolved.
If
the graphs are
very broad, then the data are poorly resolved. Even in cases where
there is no natural ordering
of
the data, the resolution matrix still
shows how much weight each observation has in influencing the
I=
1
\
\
Fig.
4.1.
Plots
of
selected rows
of
the data resolution matrix
N
indicate how well the
data can be predicted. Narrow peaks occurring near the main diagonal
of
the matrix
(dashed line) indicate that the resolution is good.

64
4
Linear,
Gaussian
Inverse
Problem, Viewpoint
2
predicted value. There is then no special significance to whether large
off-diagonal elements fall near to or far from the main diagonal.
Because the diagonal elements of the data resolution matrix indicate
how much weight a datum has in its own prediction, these diagonal
elements are often singled out and called the
importance
n
of the data
[Ref.
151:
n
=
diag(N)
(4.4)
The data resolution matrix is not a function of the data but only of the
data kernel
G
(which embodies the model and experimental geometry)
and any a priori information applied to the problem. It can therefore
be computed and studied without actually performing the experiment
and can be a useful tool in experimental design.
4.3
The
Model
Resolution Matrix
The data resolution matrix characterizes whether the data can be
independently predicted,
or
resolved. The same question can be asked
about the model parameters.
To
explore this question we imagine that
there is a true, but unknown set of model parameters
mtrue
that solve
Gmtrue
=
dabs.
We then inquire how closely a particular estimate of the
model parameters
mest
is to this true solution. Plugging the expression
for the observed data
Gmtrue
=
dobs
into the expression for the esti-
mated model
mest
=
G-gdohs
gives
(4.5)
mest
=
G-gdobs
=
G-g[Gmtrue]
=
[G-gGImtrue
=
Rmtrue
[Ref.
201
Here
R
is the
M
X
M
model
resolution matrix.
If
R
=
I,
then
each model parameter is uniquely determined. If
R
is not an identity
matrix, then the estimates of the model parameters are really weighted
averages of the true model parameters. If the model parameters have a
natural ordering (as they would
if
they represented a discretized
version of a continuous function), then plots of the rows of the
resolution matrix can be useful in determining to what scale features in
the model can actually be resolved (Fig.
4.2).
Like the data resolution
matrix, the model resolution is a function of only the data kernel and
the a priori information added to the problem. It is therefore indepen-
dent
of
the actual values of the data and can therefore be another
important tool in experimental design.

4.4
The
Unit
Covariance
Matrix
\
\
\
65
mtrue
Fig.
4.2.
Plots
of
selected rows
of
the model resolution matrix
R
indicate how
well
the
true model parameters can be resolved. Narrow peaks occurring near the main diagonal
of
the matrix (dashed line) indicate that the model
is
well resolved.
4.4 The Unit Covariance Matrix
The covariance of the model parameters depends on the covariance
of the data and the way in which error is mapped from data to model
parameters. This mapping is a function of only the data kernel and the
generalized inverse, not of the data itself. It is therefore useful to define
a
unit covariance matrix
that characterizes the degree oferror amplifi-
cation that occurs in the mapping. If the data are assumed to be
uncorrelated and all have equal variance
cr2,
the unit covariance
matrix is given
by
[cov, m]
=
o-*G-g[cov d]G-gT
=
G-gG-gT
(4.6)
Even
if
the data are correlated, one can often find some normaliza-
tion of the data covariance matrix,
so
that one can define a
unit
data
covariance matrix
[cov, d], related to the model covariance matrix by
[cov, m]
=
G-~[cov, d]G-gT
(4.7)
Because the unit covariance matrix, like the data and model resolution
matrices, is independent of the actual values and variances of the data,
it is a useful tool in experimental design.
As
an example, reconsider the problem
of
fitting a straight line to

66
4
Linear, Gaussian Inverse Problem, Viewpoint
2
Fig.
4.3.
(a) The method of least squares is used to fit a straight line to uncorrelated data
with uniform variance. The vertical bars are a measure of the error. Since the data are
not well separated in
z,
the variance of the slope and intercept is large (as indicated by
the two different lines).
(b)
Same as (a) but with the data well separated in
z.
Although
the variance ofthe data is the same as in (a) the variance
of
the intercept and slope ofthe
straight line
is
much smaller.
(z,
d)
data. The unit covariance matrix for intercept
m,
and slope
m2
is
given by
r
Note that the estimates of intercept and slope are uncorrelated only
when the data are centered about
z=O.
The overall size of the
variance is controlled by the denominator of the fraction. If all the
z
values are nearly equal, then the denominator of the fraction is small
and the variance of the intercept and slope is large (Fig. 4.3a). On the
other hand,
if
the
z
values have a large spread, the denominator is large
and the variance is small (Fig. 4.3b).
4.5
Resolution and Covariance
of
Some
Generalized Inverses
The data and model resolution and unit covariance matrices de-
scribe many interesting properties of the solutions to inverse problems.
We therefore calculate these quantities for some
of the simpler general-
ized inverses (with [cov,
d]
=
I).

4.6
Measures
of
Goodness
of
Resolution
and Covariance
67
4.5.2
MINIMUM LENGTH
G-B
=
GT[GGT]-I
N
=
GG-B
=
GGT[GGT]-l
=
1
(4.10)
R
=
G-gG
=
GT[GGT]-'G
[cov,
m]
=
G-gG-gT
=
GT[GGT]-'[GGT]-IGT
=
GT[GGT]-2GT
Note that there is a great deal of symmetry between the least squares
and minimum length solutions. Least squares solves the completely
overdetermined problem and has perfect model resolution; minimum
length solves the completely underdetermined problem and has per-
fect data resolution.
As
we shall see later, generalized inverses that
solve the intermediate mixed-determined problems will have data and
model resolution matrices that are intermediate between these two
extremes.
4.6
Measures
of
Goodness
of
Resolution
and Covariance
Just as we were able to quantify the goodness of the model parame-
ters by measuring their overall prediction error and simplicity, we shall
develop techniques that quantify the goodness of data and model
resolution matrices and unit covariance matrices. Because the resolu-
tion is best when the resolution matrices are identity matrices, one
possible measure
of
resolution is based on the size, or
spread
of the
off-diagonal elements.
