Menke W. Geophysical Data Analysis: Discrete Inverse Theory

Подождите немного. Документ загружается.

Some Comments

Probability

Theory

dl+d2

Fig.

2.9.

(a and b) The uncorrelated data d, and

both have white distributions on the

interval

[0,

I].

a rectangular area

uniform

probability. The probability distribution

for

the

sum

the joint distribution,

integrated along lines of constant

(dashed). (d) The distribution for

triangular.

Performing this line integral

the most general case can be mathe-

matically quite difficult. Fortunately, in the case of the linear function

where M and

are an arbitrary matrix and vector,

respectively,

possible to make some statements about the proper-

ties of the resultant distribution without explicitly performing the

integration. In particular, the mean and covariance of the resultant

distribution can be shown, respectively, to be

(m)

M(d)

and [cov

M[cov d]MT

(2.7)

an example, consider a model parameter

rn,

which

the mean

of a set of data

rn,

l/N~di=(l/N)[l,

l]d

(2.8)

That

is, M

[

1, 1,

]/Nand

Suppose that the data are

uncorrelated and all have the same mean

(d)

and variance

0:.

Then

2.4

Gaussian Distributions

we see that

(m,)

M(d)

(d)

and var(m,)

M[cov

d]MT

a:/N.

The model parameter

rn,

therefore, has a distribution

P(ml)

with mean

(m,

)

(d)

and a variance

a’,

a:/N.

The square root of

the variance, which is a measure

the width of the peak in

P(m,)

and

therefore a measure of the likelihood that any particular experiment

will yield an

close to the true mean, is proportional to

N-1/2.

The

accuracy of determining the mean of a group of data, therefore,

decreases very slowly as the number of observations increases.

2.4

Gaussian Distributions

The distribution for a particular random variable can be an arbi-

trarily complicated function, but in many instances data possess the

rather simple Gaussian distribution

This distribution has mean

(d)

and variance

(Fig.

2.10).

The

Gaussian distribution is

common because it is the limiting distribu-

tion for the sum of random variables. The

central

limit

theorem

shows

(with certain limitations) that regardless of the distribution of a set of

independent random variables, the distribution of their sum tends to a

Gaussian distribution as the number of summed variables increases.

long as the noise in the data comes from several sources of

comparable size,

will tend to follow a Gaussian distribution. This

0.50

0.25

-5

-4

-3

-2

-1

Fig.

2.10.

Gaussian distribution with zero mean and

for

curve

and

for

curve

Some Comments

Probability

Theory

behavior is exemplified by the sum of the two white distributions in

Section 2.3. The distribution of their sum is more nearly Gaussian

than the individual distributions (it being triangular instead of rectan-

gular).

The joint distribution for two independent Gaussian variables is just

the product of two univariate distributions. When the data are corre-

lated (say, with mean (d) and covariance [cov d]), the distribution is

more complicated, since it must express the degree of correlation. The

appropriate generalization turns out to be

exp(-i[d

(d)lT[cov d]-'[d

(d)]

[cov d]

(27p

P(d)

This distribution is chosen because it has the correct mean and

variance when the data are uncorrelated and has covariance [cov d]

when the data are correlated. It can be shown that all linear functions

Gaussian random variables are also Gaussian random variables

with a distribution of this form.

The idea that the model and data are related by an explicit relation-

ship g(m)

d can be reinterpreted in light of this probabilistic descrip-

tion of the data. We can no longer assert that this relationship can hold

for the data themselves, since they are random variables. Instead, we

assert that this relationship holds for the mean data: g(m)

(d). The

distribution for the data can then be written as

~[COV

dj1-'/2

exp

[

-7

g(m)lT[cov d]-'[d

g(m)]] (2.1

(27p

P(d)

The model parameters now have the interpretation of a set of un-

known quantities that define the shape of the distribution for the data.

One approach to inverse theory (which will be pursued in Chapter

to try to use the data to determine the distribution, and thus the values

of the model parameters.

For

the Gaussian distribution [Eq. (2.1 l)] to be sensible, g(m) must

not be a function

any random variables. This is why we differen-

tiated between data and auxi!iary variables in Chapter

the latter

must be known exactly. If the auxiliary variables are themselves

uncertain, then they must be treated as data and the inverse problem

becomes an implicit one with a much more complicated distribution

than the above problem exhibits.

an example of constructing the distribution for a set of data,

consider an experiment in which the temperature

in some small

2.5

Testing the Assumption

Gaussian Statistics

volume of space is measured

times. If the temperature is assumed

not to be a function

time and space, the experiment can

viewed as

the measurement of

realizations of the same random variable or as

the measurement of one realization of

distinct random variables

that all have the same distribution. We adopt the second viewpoint.

If the data are independent Gaussian random variables with mean

(d)

and variance

03,

then we can represent the assumption that all the

data have the same mean by an equation of the form

[mil

(2.12)

where

is a single model parameter. We can then compute explicit

formulas for the expressions in

P(d)

Gm]*[cov d]-'[d

Gm]

ai2

(di

ml)2

The joint distribution is therefore

P(d)

a;N

exp[--a;2x(di-

mJ2]

(2.14)

(27p2 2

i-1

2.5

Testing the Assumption

Gaussian Statistics

In the following chapters we shall derive methods of solving inverse

problems that are applicable whenever the data exhibit Gaussian

statistics. In many instances the assumption that the data follow this

distribution is a reasonable one; nevertheless, it is important to have

some means of testing this assumption.

First, consider a set of

random variables

xi,

each possessing a

Gaussian distribution with zero mean and unit variance. Suppose we

Some Comments

Probability

Theory

construct a new random variable

(2.15)

This random variable is said to have thex2 distribution with

degrees

of freedom. This distribution can be shown to be unimodal with mean

and variance 2v and to have the functional form

(2.16)

where is the gamma function. We shall make use of this distribution

in the discussion to follow.

We begin by supposing that we have some method of solving the

inverse problem for the estimated model parameters. Assuming fur-

ther that the model

explicit, we can compute the variation ofthe data

about its estimated mean

a quantity we refer to as the error

g(mest).

Does this error follow an uncorrelated Gaussian distribution

with uniform variance?

test the hypothesis that it does, we first make a histogram of the

errors

e,,

in which the histogram intervals have been chosen

that

there are about the same number of errors

in each interval. This

histogram is then normalized to unit area, and the area

of each of

the, say,

intervals is noted. We then compare these areas with the

areas

given by a Gaussian distribution with the same mean and

variance as the

e,.

The overall difference between these areas can be

quantified by using

(A’

Ai)2

X2’C

(2.17)

the data followed a Gaussian distribution exactly, then

should

be close to zero (it will not

zero since there are always random

fluctuations). We therefore need to inquire whether the

measured

for any particular data set is sufficiently far from zero that it is

improbable that the data follow the Gaussian distribution. This is

done by computing the theoretical distribution of

and seeing

whether

is probable. The usual rule for deciding that the data do

not follow the assummed distribution is that values greater than

equal to

occur less than

of the time (if many realizations

the

entire experiment were performed).

2.6

Confidence Intervals

The quantity

can be shown to follow approximately a

distri-

bution, regardless of the type of distribution involved. This method

can therefore be used to test whether the data follow any given

distribution. The number ofdegrees

freedom is given byp minus the

number of constraints placed on the observations. One constraint is

that the total area

is unity. Two more constraints come from the

fact that we assumed a Gaussian distribution and then estimated the

mean and variance from the

el.

The Gaussian case, therefore, has

This test is known as the

test.

The

distribution is

tabulated in most texts on statistics.

2.6

Confidence

Intervals

The confidence of a particular observation is the probability that

one realization of the random variable falls within a specified distance

of the true mean. Confidence is therefore related to the distribution of

area in

P(d).

most ofthe area is concentrated near the mean, then the

interval for, say,

95%

confidence will be very small; otherwise, the

confidence interval will be large. The width of the confidence interval

is related to the variance. Distributions with large variances will also

tend to have large confidence intervals. Nevertheless, the relationship

is not direct, since variance is a measure

width, not area. The

relationship is easy to quantify for the simplist univariate distribu-

tions.

For

instance, Gaussian distributions have

68%

confidence inter-

vals

wide and

95%

confidence intervals

wide. Other types of

simple distributions have similar relationships.

one knows that a

particular Gaussian random variable has

then if a realization of

that variable has the value

50,

one can state that there is a

95%

chance

that the mean of the random variable lies between

and

(one

might symbolize this

(d)

2).

The concept of confidence intervals is more difficult to work with

when one is dealing with several correlated data. One must define

some volume in the space of data and compute the probability that the

true means of the data are within the volume. One must also specify

the shape of that volume. The more complicated the distribution, the

more difficult it is to chose an appropriate shape and calculate the

probability within it.

This page intentionally left blank

SOLUTION

THE

LINEAR, GAUSSIAN

INVERSE PROBLEM,

VIEWPOINT

THE

LENGTH METHOD

3.1

The Lengths

Estimates

The simplest of methods for solving the linear inverse problem

is based on measures of the size, or length,

the estimated

model parameters

mest

and

the predicted data

dPR

Gmest.

see that measures

length can

relevant to the solution of

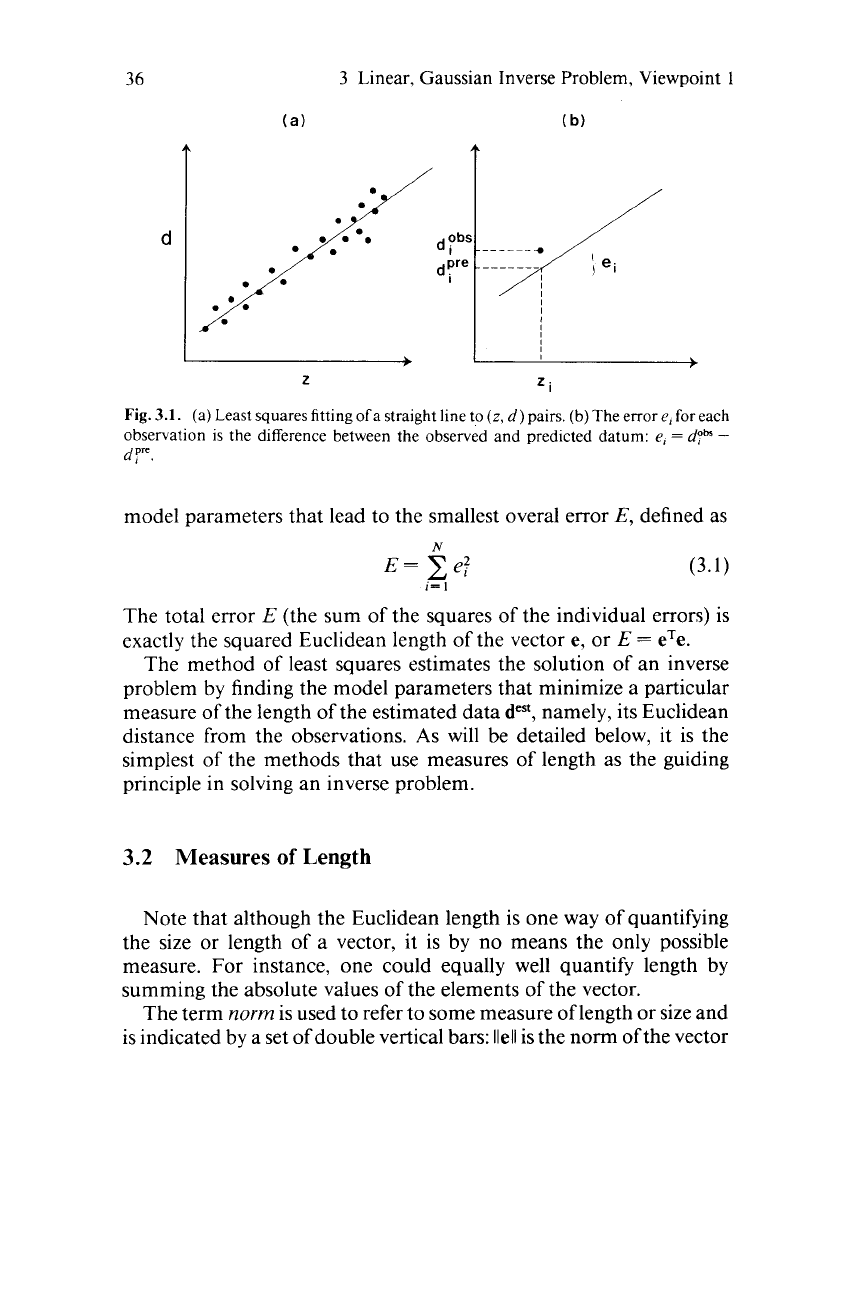
inverse problems, consider the simple problem of fitting a straight line

to data (Fig.

3.1).

This problem is often solved by the

called method

of least squares. In this method one tries to pick the model parameters

(intercept and slope)

that the predicted data are as close as possible

to the observed data. For each observation one defines a prediction

error, or misfit,

dpb”

dym.

The best fit-line is then the one with

Linear, Gaussian Inverse Problem,

Viewpoint

‘i

Fig.

3.1.

(a)

Least

squares fitting

ofa

straight line to

(z,

pairs. (b) The error e, for each

observation

the difference between the observed and predicted datum: e,

dph

dy.

model parameters that lead to the smallest overal error

defined as

CeT

The total error

(the sum of the squares of the individual errors) is

exactly the squared Euclidean length of the vector

eTe.

The method of least squares estimates the solution of an inverse

problem by finding the model parameters that minimize a particular

measure of the length of the estimated data

dest,

namely, its Euclidean

distance from the observations.

will be detailed below, it

the

simplest of the methods that use measures of length as the guiding

principle in solving an inverse problem.

3.2

Measures

Length

Note that although the Euclidean length is one way of quantifying

the size or length of a vector, it is by no means the only possible

measure. For instance, one could equally well quantify length by

summing the absolute values of the elements of the vector.

The term

norm

is used to refer to some measure of length or size and

is indicated by a set of double vertical bars:

llell

is the norm of the vector

3.2

Measures

Length

The most commonly employed norms are those based on the sum of

some power of the elements of a vector and are given the name

L,,

where

is the power:

(3.2a)

(3.2~)

Successively higher norms give the largest element of

successively

larger weight. The limiting case of

gives nonzero weight to only

the largest element; therefore, it is equivalent to the selection of the

vector element with largest absolute value as the measure of length,

and is written as

norm:

llell,

max

le,l

(3.2d)

The method ofleast squares uses the

norm to quantify length. It is

appropriate to inquire why this, and not some other choice of norm, is

used. The answer involves the way in which one chooses to weight data

that fall far from the average trend (Fig.

3.2).

If the data are very

accurate, then the fact that one prediction falls far from its observed

value

important.

high-order

norm

is used, since it weights the

larger errors preferentially. On the other hand, if the data are expected

to scatter widely about the trend, then no significance can be placed

upon a few large prediction errors.

A low-order norm is used, since it

gives more equal weight to errors of different size.

will be discussed in more detail later, the

norm implies that the

data obey Gaussian statistics. Gaussians are rather short-tailed distri-

butions,

so it is appropriate to place considerable weight on any data

that have a large prediction error.

The likelihood of an observed datum falling far from the trend

depends on the shape of the distribution for that datum. Long-tailed