Menke W. Geophysical Data Analysis: Discrete Inverse Theory
Подождите немного. Документ загружается.

78
4
Linear, Gaussian Inverse Problem, Viewpoint
2
I
SDre2.d
of
resolution
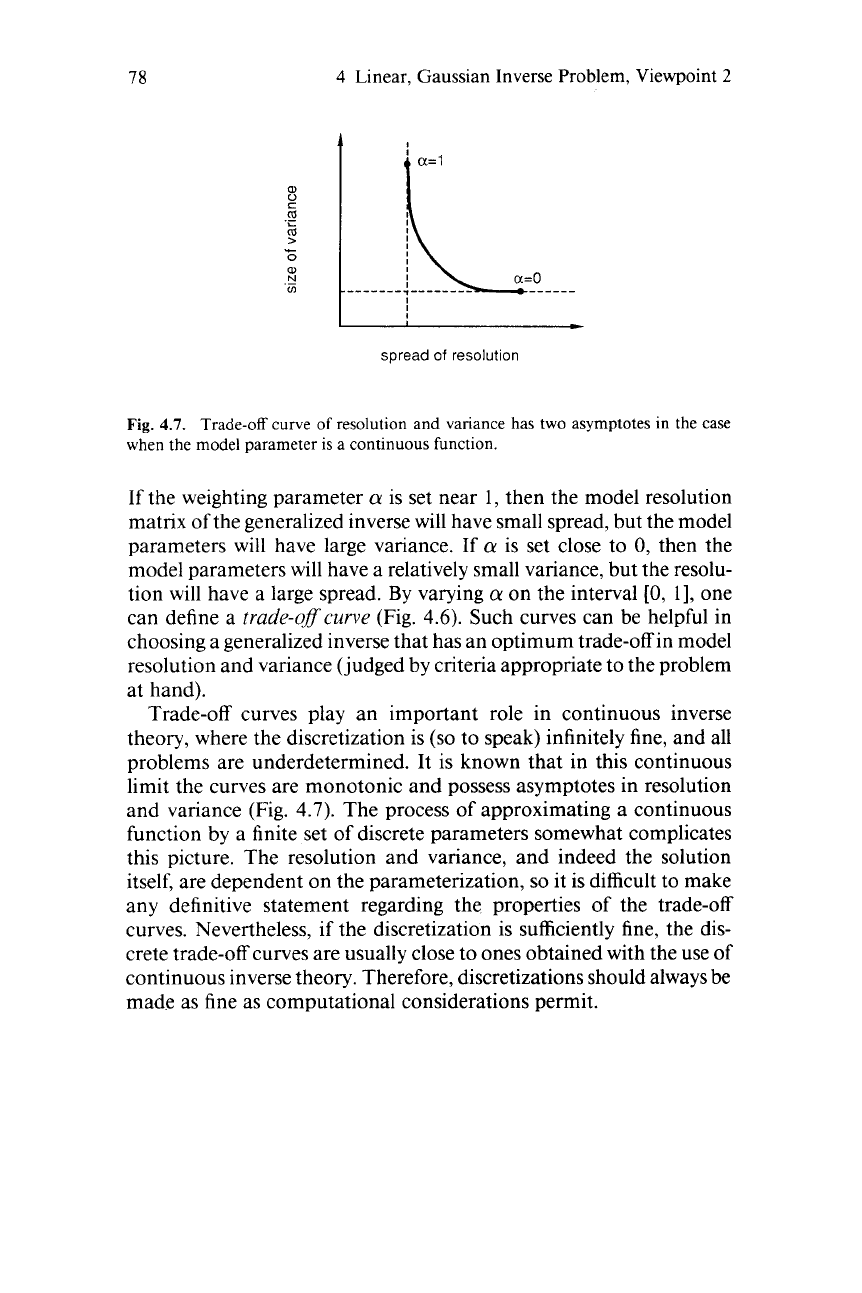
Fig.
4.7.
Trade-off curve
of
resolution and variance has two asymptotes in the case
when the model parameter
is
a continuous function.
If
the weighting parameter
a
is set near
1,
then the model resolution
matrix of the generalized inverse will have small spread, but the model
parameters will have large variance. If
a
is set close to
0,
then the
model parameters will have a relatively small variance, but the resolu-
tion will have a large spread. By varying
a
on the interval
[O,
11,
one
can define a
trade-oflcuwe
(Fig.
4.6).
Such curves can be helpful in
choosing a generalized inverse that has an optimum trade-off in model
resolution and variance (judged by criteria appropriate to the problem
at hand).
Trade-off curves play an important role in continuous inverse
theory, where the discretization is
(so
to speak) infinitely fine, and all
problems are underdetermined. It is known that in this continuous
limit the curves are monotonic and possess asymptotes in resolution
and variance (Fig.
4.7).
The process of approximating a continuous
function by a finite set of discrete parameters somewhat complicates
this picture. The resolution and variance, and indeed the solution
itself, are dependent on the parameterization,
so
it is difficult to make
any definitive statement regarding the properties of the trade-off
curves. Nevertheless, if the discretization is sufficiently fine, the dis-
crete trade-off curves are usually close to ones obtained with the use of
continuous inverse theory. Therefore, discretizations should always be
made as fine as computational considerations permit.

SOLUTION OF
THE
LINEAR, GAUSSIAN
INVERSE PROBLEM,
VIEWPOINT
3:
MAXIMUM
LIKELIHOOD METHODS
5.1
The Mean
of
a
Group
of
Measurements
Suppose that an experiment is performed
N
times and that each
time a single datum
d,
is collected. Suppose further that these data are
all noisy measurements
of
the same model parameter
rn,
.
In the view
of probability theory,
N
realizations of random variables, all of which
have the same distribution, have been measured. If these random
variables are Gaussian, their joint distribution can be characterized in
terms of a variance
d
and a mean
rn,
(see Section
2.4)
as
P(d)
=
0-~(277)-~/~
exp
--
cr2
(di
-
rn,)2]
N
(5.1)
79
2
i-I
"

80
5
Linear, Gaussian Inverse Problem, Viewpoint
3
Fig.
5.1.
The data are represented by a single point in a space whose dimension equals
the number
of
observations (in this case,
3).
These data are realizations
of
random
variables with the same mean and variance. Nevertheless, they
do
not necessarily fall on
the line d,
=
d,
=
d3
(dashed).
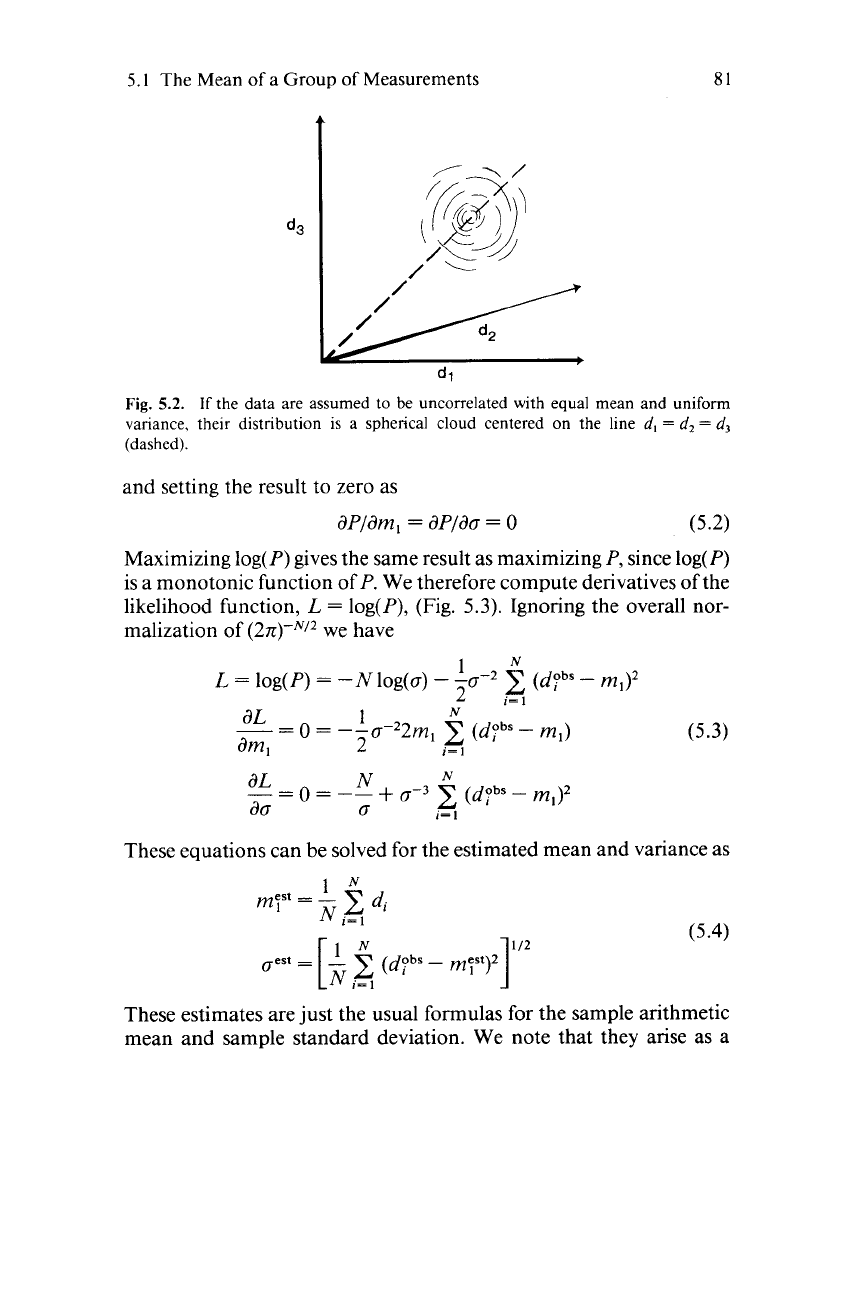
The data dobs can be represented graphically as a point in the
N-dimensional space whose coordinate axes are
d,
,
d2,
. . .
,
dN.
One
such graph is shown in Fig.
5.1.
The probability distribution for the
data can also be graphed (Fig.
5.2).
Note that the distribution is
centered about the line
d,
=
d2
=
* * *
=
dN,
since all the
d;s
are
supposed to have the same mean, and that it is spherically symmetric,
since all the
di’s
have the same variance.
Suppose that we guess a value for the unknown data mean and
variance, thus fixing the center and diameter of the distribution. We
can then calculate the numerical value of the distribution at the data,
P(dobs).
If
the guessed values of mean and variance are close to being
correct, then
P(dobs)
should be a relatively large number.
If
the guessed
values are incorrect, then the probability, or
likelihood,
ofthe observed
data will be small. We can imagine sliding the cloud of probability in
Fig.
5.2
up along the line and adjusting its diameter until its probability
at the point dobs is maximized.
This procedure defines a method of estimating the unknown param-
eters in the distribution, the
method
of
maximum likelihood.
It
asserts
that the optimum values of the parameters maximize the probability
that the observed data are in fact observed. In other words, the
probability at the point dobsis made as large as possible. The maximum
is located by differentiating
P(dobS)
with respect to mean and variance
5.1
The Mean
of
a Group
of
Measurements
81
t
dl
Fig.
5.2.
If
the data are assumed to be uncorrelated with equal mean and uniform
variance, their distribution is a spherical cloud centered on the line
d,
=
d,
=
d3
(dashed).
and setting the result to zero as
dPlam,
=
aP/&
=
0
(5.2)
Maximizing log(
P)
gives the same result as maximizing
P,
since log(
P)
is a monotonic function of
P.
We therefore compute derivatives of the
likelihood function,
L
=
log(P),
(Fig.
5.3).
Ignoring the overall nor-
malization of
(27~)-”~
we have
IN
2
i-1
L
=
log(
P)
=
-
N
log(a)
-
-r2
(dpbs
-
mJ2
2
(dpbs
-
m,)
dL
1
-
=
0
=
--g-22ml
am,
2
i=
1
(5.3)
These equations can be solved for the estimated mean and variance as
These estimates are just the usual formulas for the sample arithmetic
mean and sample standard deviation. We note that they arise as a
82
5
Linear, Gaussian Inverse Problem, Viewpoint
3
t
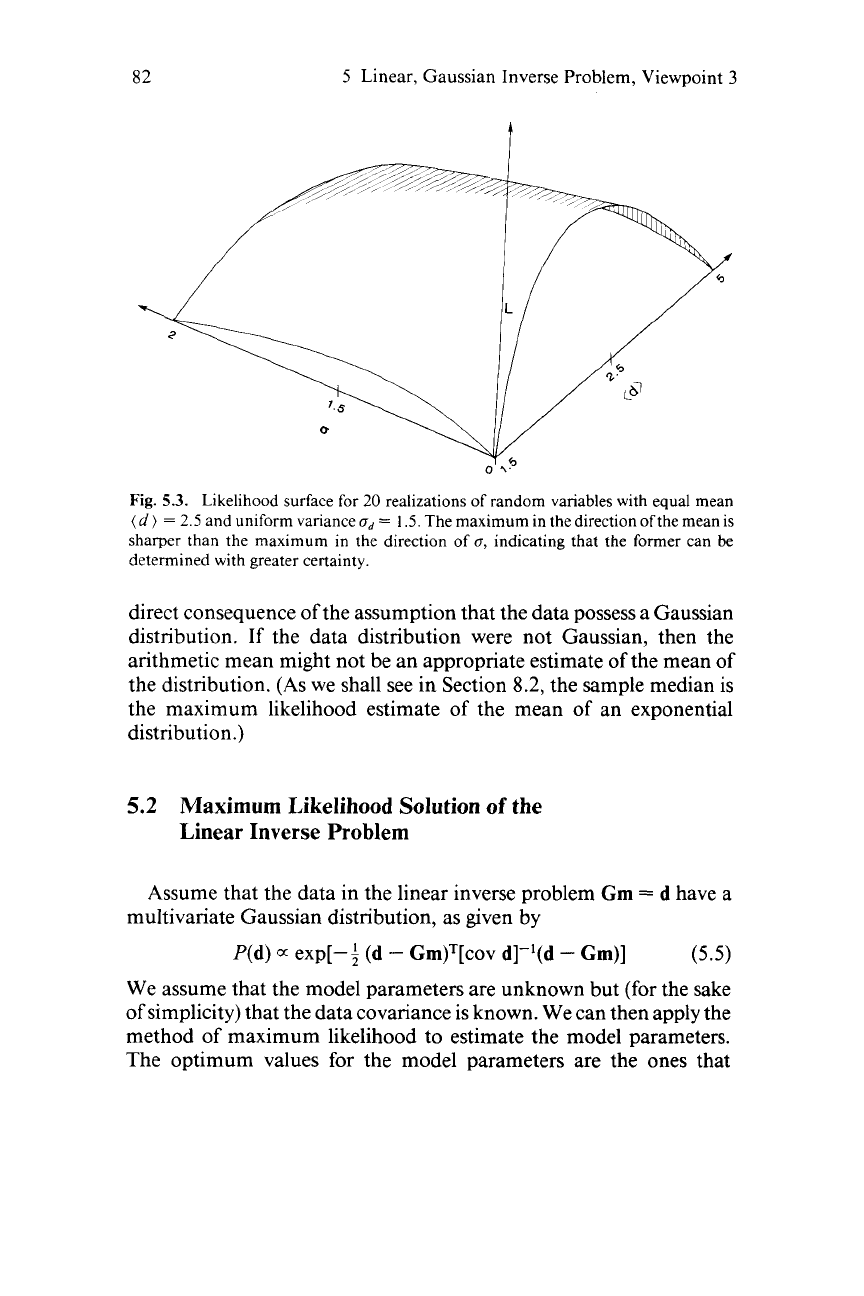
Fig.
5.3.
Likelihood surface for 20 realizations
of
random variables with equal mean
(d
)
=
2.5 and uniform variance
u,
=
1.5. The maximum in the direction ofthe mean
is
sharper than the maximum in the direction
of
u,
indicating that
the
former can
be
determined with greater certainty.
direct consequence of the assumption that the data possess a Gaussian
distribution.
If
the data distribution were not Gaussian, then the
arithmetic mean might not be an appropriate estimate
of
the mean
of
the distribution. (As we shall see in Section
8.2,
the sample median is
the maximum likelihood estimate of the mean of an exponential
distribution.)
5.2
Maximum Likelihood Solution
of
the
Linear Inverse Problem
Assume that the data in the linear inverse problem Gm
=
d
have a
multivariate Gaussian distribution, as given by
P(d)
cc
exp[-;
(d
-
Gm)=[cov d]-'(d
-
Gm)]
(5.5)
We assume that the model parameters are unknown but (for the sake
of simplicity) that the data covariance is known. We can then apply the
method of maximum likelihood to estimate the model parameters.
The optimum values for the model parameters are the ones that

5.3
A
Priori Distributions
83
maximize the probability that the observed data are in fact observed.
Clearly, the maximum of
P(dobs)
occurs when the argument of the
exponential is a maximum, or when the quantity given by
(d
-
Gm)=[cov
d]-'(d
-
Gm)
(5.6)
is a minimum. But this expression is just a weighted measure of
prediction length. The maximum likelihood estimate of the model
parameters is nothing but the weighted least squares solution, where
the weighting matrix is the inverse of the covariance matrix of the data
(in the notation of Chapter
3,
W,
=
[cov
d]-').
If the data happen to be
uncorrelated and all have equal variance, then [cov
d]
=
031,
and the
maximum likelihood solution is the simple least squares solution. If
the data are uncorrelated but their variances are all different (say,
a:,),
then the prediction error is given by
N
E
=
aZ2ef
i-
1
(5.7)
where
ei
=
(dpbs
-
dp'")
is the prediction error for each datum. Each
measurement is weighted by the reciprocal of its variance; the most
certain data are weighted most.
We have justified the use of the
L,
norm through the application
of
probability theory. The least squares procedure for minimizing the
L,
norm of the prediction error makes sense if the data are uncorrelated,
have equal variance, and obey Gaussian statistics. If the data are not
Gaussian, then other measures of prediction error may
be
more
appropriate.
5.3
A
Priori Distributions
If
the linear problem is underdetermined, then the least squares
inverse does not exist. From the standpoint of probability theory, the
distribution of the data
P(dobs)
has
no
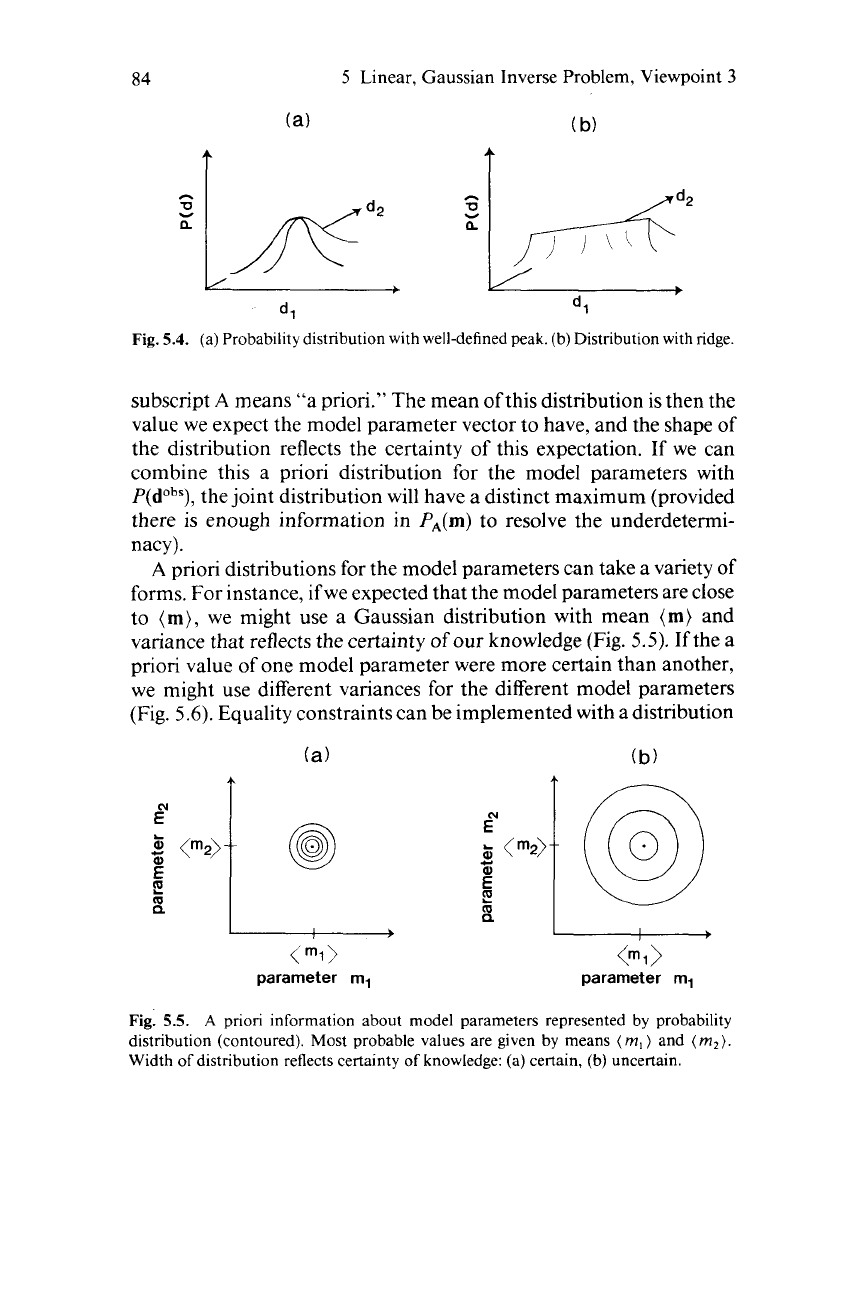
well-defined maximum with
respect to variations of the model parameters. At best, it has a ridge of
maximum probability (Fig.
5.4).
To solve this underdetermined problem we must add a priori
information that causes the distribution to have a well-defined peak.
One way to accomplish this is to write the a priori information about
the model parameters as a probability distribution P,(m), where the
84
5
Linear, Gaussian Inverse Problem, Viewpoint
3
Fig.
5.4.
(a)
Probability distribution with well-defined peak.
(b)
Distribution with ridge.
subscript
A
means “a priori.” The mean of this distribution is then the
value we expect the model parameter vector to have, and the shape of
the distribution reflects the certainty of this expectation.
If
we can
combine this a priori distribution for the model parameters with
P(dobs),
the joint distribution will have a distinct maximum (provided
there
is
enough information in
P,(m)
to resolve the underdetermi-
nacy).
A
priori distributions for the model parameters can take a variety of
forms. For instance, if we expected that the model parameters are close
to
(m),
we might use a Gaussian distribution with mean
(m)
and
variance that reflects the certainty of our knowledge (Fig.
5.5).
If the a
priori value of one model parameter were more certain than another,
we might use different variances for the different model parameters
(Fig.
5.6).
Equality constraints can be implemented with a distribution
(a)
(b)
<“I>
parameter
ml
<“I>
parameter
ml
Fig.
5.5.
A
priori information about model parameters represented by probability
distribution (contoured). Most probable values are given by means
(m,
)
and
(
m2).
Width of distribution reflects certainty
of
knowledge: (a) certain,
(b)
uncertain.
5.3
A
Priori
Distributions
85
parameter ml
Fig.
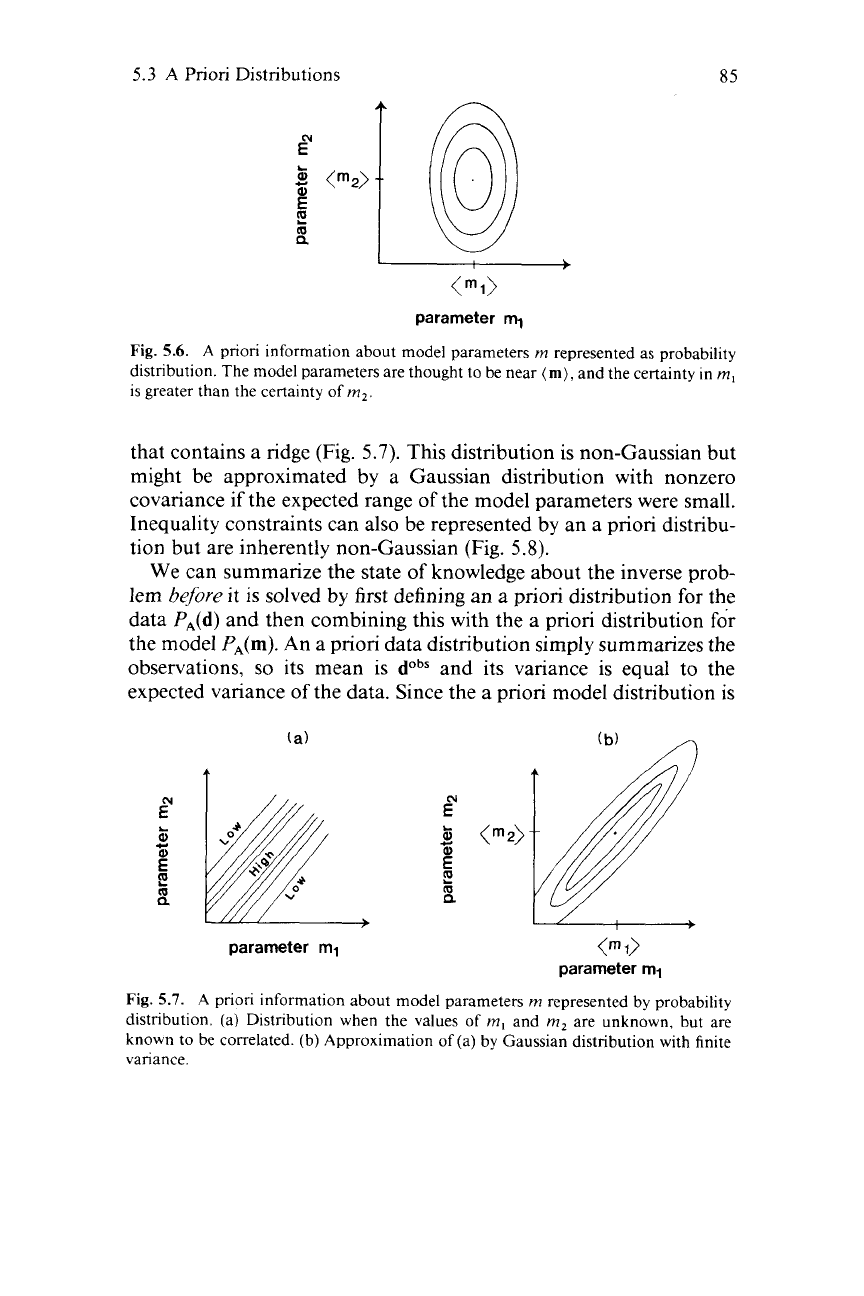
5.6.
A priori information about model parameters
m
represented as probability
distribution. The model parameters are thought to be near
(m),
and the certainty
in
m,
is
greater than the certainty
of
m2.
that contains a ridge (Fig.
5.7).
This distribution is non-Gaussian but
might be approximated by a Gaussian distribution with nonzero
covariance
if
the expected range of the model parameters were small.
Inequality constraints can also be represented by an a priori distribu-
tion but are inherently non-Gaussian (Fig.
5.8).
We can summarize the state of knowledge about the inverse prob-
lem
before
it
is
solved by first defining an a prion distribution for the
data
P,(d)
and then combining this with the a priori distribution for
the model
P,(m).
An a priori data distribution simply summarizes the
observations,
so
its mean is
dobs
and its variance is equal to the
expected variance of the data. Since the a priori model distribution is
parameter ml
<m
1)
parameter ml
Fig.
5.7.
A
priori
information about model parameters
rn
represented by probability
distribution. (a) Distribution when the values
of
m,
and
m2
are unknown, but are
known
to be correlated. (b) Approximation
of
(a) by Gaussian distribution with finite
variance.

86
5
Linear, Gaussian Inverse Problem, Viewpoint
3
"I
Fig.
5.8.
A
priori information about model parameters
rn
represented as a probability
distribution (contoured) when
rn,
i
m,.
Such distributions are inherently non-Gaus-
sian.
completely independent
of
the actual values
of
the data, we can
form
the joint a priori distribution simply by multiplying the two as
PA(m, d)
=
PA(m)PA(d)
(5.8)
This distribution can be depicted graphically as a "cloud"
of
probabil-
ity centered on the observed data and a priori model, with a width that
reflects the certainty
of
these quantities
(Fig.
5.9).
Note that,
if
we
I
I
b
map
model
m
Fig.
5.9.
Joint probability distribution
for
observed data and a priori model parame-
ters.

5.4
Maximum
Likelihood
for
an Exact
Theory
87
apply the maximum likelihood method to this distribution, we simply
recover the data and a priori model. We have not yet applied our
knowledge of the model (the relationship between data and model
parameters).
5.4
Maximum Likelihood for an Exact
Theory
Suppose that the model is the rather general equation
g(m)
=
d
(which may or may not be linear). This equation defines a surface in
the space of model parameters and data along which the solution must
lie (Fig.
5.10).
The maximum likelihood problem then translates into
finding the maximum of the joint distribution
P,(m,
d)
on the surface
d
=
g(m)
[Ref.
181.
Note that
if
the a priori distribution for the model
parameters is much more certain than that of the observed data (that
is, if
a,
<<
ad),
then the estimate of the model parameters (the
maximum likelihood point) tends to be close to the a priori model
parameters (Fig.
5.1
1).
On the other hand,
if
the data are far more
t
U
5
4-
m
-0
1
I'
I
I
/'
I
I
I
I
map
I
+
model
m
Fig.
5.10.
The estimated model parameters
mest
(triangle) and predicted data
dp"
fall
on
the theoretical curve
g(m)
=
d
(solid curve).
