Меледин Т.В., Черкасский В.С. Электродинамика в задачах. Часть 1. Электродинамика частиц и полей
Подождите немного. Документ загружается.

200
ОТВЕТЫ, УКАЗАНИЯ
2.34. σ = −
5
√
5−1
20π
√
5
Q
a
2
.
2.35. а) ϕ (z) =
q
√
a
2
+z
2
−
qa
√
a
4
+b
2
z
2
;
б) ϕ (r, θ) =
q
r
1 −
a
b
+
qb
2
4r
3
1 −
a
5
b
5
3 cos
2
θ − 1
.
2.36. а) ϕ (z) =
Q
√
b
2
+z
2
+
Q
0
√
b
02
+(z+a−z
0
)
2
−
Q
0
|z+a|
, где b
0
= b
a
2
a
2
+b
2
-
радиус кольца изображения, Q
0
= −Q
a
√
a
2
+b
2
- его заряд и z
0
=
a
3
a
2
+b
2
- расстояние от его плоскости до центра сферы;
б) ϕ (r, θ) =
Q
r
+
Qa
4
cos θ
(
a
2
+b
2
)
3/2
r
2
.
2.37. F
r
=
2κ
2
a
`
2
−a
2
.
2.38. σ (R) = −
aq
2π
(
a
2
+R
2
)
3/2
.
2.39. ϕ
1
=
q
ε
1
r
1
+
1
ε
1
q
ε
1
−ε
2
ε
1
+ε
2
1
r
2
,
ϕ
2
=
1
ε
2
q
2ε
2
ε
1
+ε
2
1
r
1
.
2.40. σ
связ
=
q
ε
1
ε
1
−ε
2
ε
1
+ε
2
a
2πR
3
,
при ε
2
→ ∞, σ
связ
= −
qa
2πε
1
R
3
(ср. с 2.22.)
2.41.F
z
=
3p
2
16h
4
ε
1
−ε
2
ε
1
(ε
1
+ε
2
)
, N = 0.
2.42. F
z
= −
2κ
2
ε
1
h
ε
1
−ε
2
ε
1
+ε
2
.
2.43. F =
q
2
1
4a
2
ε
1
ε
1
−ε
2
ε
1
+ε
2
+
2q
1
q
2
(ε
1
+ε
2
)a
2
+
q
1
q
3
2a
2
(ε
2
+ε
1
)
.
2.44. F
1
=
q
2
1
4a
2
ε
1
ε
2
−ε
1
ε
1
+ε
2
+
q
1
q
2
4a
2
ε
1
2ε
1
ε
1
+ε
2
, F
2
=
q
2
2
4a
2
ε
2
ε
2
−ε
1
ε
1
+ε
2
+
q
2
q
1
4a
2
ε
2
2ε
2
ε
1
+ε
2
.
2.4. Энергия поля. Давление. Силы
2.45. A
нов
= A/
√
2, т. к. A ∼ q
2
/`.
2.46. A
нов
= 6A.
2.47. а) ∆W =
(1−ε)CU
2
2
; б) ∆W =
(1−ε)Q
2
2εC
, A = ∆W , C =
S
4πd
.
2.48. W =
3
5
Q
2
R
.
2.49. W =
5
4
e
2
a
.

2.4 Энергия поля. Давление. Силы
201
2.50. W =
(~p
1
~p
2
)
r
3
−
3(~p
1
~r)(~p
2
~r)
r
5
=
p
1
p
2
r
3
(sin θ
1
sin θ
2
cos ϕ − 2 cos θ
1
cos θ
2
),
где θ
1
=
c
~r, ~p
1
, θ
2
=
c
~r, ~p
2
, ϕ - угол между плоскостями (~p
1
, ~r)
и (~r, ~p
2
); F
r
= 3W/r, F максимальна, когда диполи параллельны, и
равна F
max
= −6p
1
p
2
/r
4
(притяжение!).
2.51. W = −
p
2
16εa
3
1 + cos
2
θ
, где θ = (
d
~p, ~e
z
);
F
z
= −
3W
a
, N
θ
= −
p
2
sin 2θ
16εa
3
.
2.52. W = −
Q(~p
0
~r
∗
)
2εr
∗3
+
(~p
0
~p)
2εr
∗3
−
3(~p
0
~r
∗
)(~p~r
∗
)
2εr
∗5
, где заряд изображения
Q =
(~p~r)
r
3
R и диполь изображения ~p = −~p
0
R
3
r
3
+ 2
(~p
0
~r)~r
r
2
R
3
r
3
отстоят
от диполя ~p
0
на расстояние r
∗
= r − R
2
/r, а ~r, ~r
∗
- радиус-векторы
положения диполя ~p
0
и его изображений соответственно.
Если θ =
c
~p, ~r
, то W = −
p
2
0
R
(
R
2
+r
2
cos
2
θ
)
2ε
(
r
2
−R
2
)
3
,
F
r
= −
p
2
0
Rr
ε
(
R
2
+2r
2
)
cos
2
θ+3R
2
(
r
2
−R
2
)
4
, N
0
= −
p
2
0
Rr
2
sin 2θ
2ε
(
r
2
−R
2
)
3
.
2.53. F
верх
= εF
нижн
= 2πq
2
/`
2
.
2.54. h =
ε−1
8πρg
E
2
d
2
.
2.55. F =
2πDd(D−d)q
2
a[b(D−d)+xd]
2
.
2.56. q = R (ε + 1)
q
2
ε−1
2
3
πR
3
ρg − mg
.
2.57. Q = −q/2.
2.58. F = q
2
4R
2
.
2.59. F = (9/16) · E
2
0
a
2
.
2.60. σ = πR
2
1 + 2
q
e
2
/R
mv
2
.
2 61. а)
dσ
dΩ
=
πR
2
8
e
2
/
R
mv
2
/2
θ
−3
; б)
dσ
dΩ
=
πR
2
8
q
3
π
e
2
/
R
mv
2
θ
−5/2
;
в)
dσ
dΩ
=
πR
2
8
q
3
π
e
2
/
R
mv
2
ε−1
ε+2
θ
−5/2
; г)
dσ
dΩ
=
1
16
3
q
15π
2
βe
3
mv
2
θ
−7/2
.
202
ОТВЕТЫ, УКАЗАНИЯ
3.1. Сохранение заряда. Граничные условия. Закон Ома
3.1. j
верх
= envr/2, j
нижн
= enva
2
/2r.
3.2.
~
j =
~
j
0
, v =
p
v
2
0
+ 2qE`/m, n = j
0
/ (qv) .
3.3. τ = ε/ (4πσ) .
3.4. tg α
1
/ tg α
2
= σ
1
/σ
2
, где α - угол "падения"линии тока на
поверхность раздела.
3.5. ϕ (r) = U[1 − (a/r)
n
]/[1 − (a/b)
n
]; R = [(b/a)
n
− 1] / (2πσ
max
n),
где σ
max
= αb
n
.
3.6. ϕ (r) = U
ln
r
R
1
/
ln
R
2
R
1
.
3.7. j
α
=
σU/(2π−α
0
)
r
, R =
2π−α
σ ln b/a
.
3.8. σ
R
1
=
J
z
4π
2
R
3
1
σ
1
ln R
1
/R
2
, σ
R
2
= −
J
z
4π
2
R
2
1
R
2
σ
·
1
ln R
1
/R
2
.
z - координата вдоль оси цилиндра. Сечение, на котором σ
R
1
=
σ
R
2
= 0, не определено и может быть смещено по z сообщением про-
воду добавочного постоянного заряда.
3.9. E
1,2
=
σ
2,1
U
`
1
σ
2
+`
2
σ
1
, σ
своб
=
(σ
1
ε
2
−ε
1
σ
2
)
4π(`
1
σ
2
+`
2
σ
1
)
U, σ
связ
= −
σ
1
(ε
2
−1)−σ
2
(ε
1
−1)
4π(`
1
σ
2
+`
2
σ
1
)
U.
К положительно заряженной обкладке конденсатора прилегает пер-
вый слой.
3.10. ϕ (x) = U
ln(1+αx/σ
1
)
ln(1+αd/σ
1
)
, ρ (x) =
Uα
2
4π(σ
1
+αx)
2
.
3.11. σ
своб
=
U
4πc
2
σ
2
ε
1
−σ
1
ε
2
σ
1
(1/c−1/b)+σ
2
(1/a−1/c)
.
3.12. E
0
= −k (σ
2
`
1
+ σ
1
`
2
) E
0
, E
1
= kσ
2
`
0
E
0
, E
2
= kσ
1
`
0
E
0
,
где k = σ
0
/ [`
0
(`
0
σ
1
σ
2
+ `
1
σ
0
σ
2
+ `
2
σ
0
σ
1
)], E
0
= E
стор.
· `
0
- э.д.с.
источника. Внутри источника поле и ток противоположно направле-
ны (E
0
< 0). Заряды сосредоточены на границах раздела проводни-
ков и равны q
01
= r
2
(E
1
− E
0
) /4, q
12
= r
2
(E
2
− E
1
) /4, q
20
=
r
2
(E
0
− E
2
) /4.
3.13. (j
i
)
r
=
Uσ
i
r ln b/a
, i = 1, 2.
3.14. J =
αU − R − r
0
+
q
(αU − R − r
0
)
2
+ 4αUR
/2αR.
3.1 Сохранение заряда. Граничные условия. Закон Ома
203
3.15. Ток в звене A
k
A
k+1
равен J
k
=
E ch(β−k)α
R
i
ch βα+
√
Rr sh(β+1/2)α
, где
параметры α и β определяются из sh (α/2) =
p
R/r/2 и tg βα =
R
a
ch nα+
√
Rr sh(n+1/2)α
R
a
sh nα+
√
Rr ch(n+1/2)α
. Ток нагрузки равен J
n
. При сухой изоляции
(r → ∞, α → 0, β → n + 1/2 + R
a
/R) искомое отношение э.д.с. рав-
но
E
E
0
=
R
i
ch βα+
√
Rrsh(β+1/2)α
[R
i
+R
a
+(n+1)R] ch(β−n)α
. При R
a
= 0 β = n + 1/2.
3.16. ϕ (x) = −ρ
0
dJ
dx
, J = −
1
ρ
dϕ
dx
,
d
2
J
dx
2
= J
ρ
ρ
0
,
d
2
ϕ
dx
2
= ϕ
ρ
ρ
0
. Размер-
ности величин: [ρ] = Ом/см, [ρ
0
] = Ом· см.
3.17. J (x) =
E ch Ω(x−x
0
)
R
i
ch Ωx
0
+
√
ρρ
0
sh Ωx
0
, где Ω =
p
ρ/ρ
0
, а x
0
опреде-
ляется из th Ω(x
0
− a) = −R
a
/
√
ρρ
0
. При R
a
= 0 (закороченная
линия) J (x) =
E ch Ω(a−x)
R
i
ch Ωa+
√
ρρ
0
sh Ωa
'
E
Ωa
ch Ω(a−x)
R
i
+ρ
0
/`
. Для сухой изоляции
(1/ρ
0
→ 0) J (x) = E/ (R
i
+ R
a
+ ρ`) = const.
3.18. R =
1
2πσ
2
1
a
−
1
b
+
1
2πσ
1
1
b
.
3.19. R =
1
2πσ
1
a
1
+
1
a
2
−
4
`
'
1
2πσ
1
a
1
+
1
a
2
.
3 20. C =
ε
4πσR
.
3.21. R =
π+ln `/a
2πσ`
, E '
U`
2r
2
ln `/a
, ∆U
шаг
'
U`λ
2r
2
ln `/a
.
3.22. k = 4πσ/ω.
3.23. а)
~
E = 0, при r < R
1
, E
r
∼ e
−
4πσt
ε
при R
1
< r < R
2
,
E
r
=
q
r
2
= const при r > R
2
; б) Q =
q
2
2ε
1
R
1
−
1
R
2
.
3.24.
~
j
нар
=
~
j
0
1 +
R
3
2r
3
−
3
2
(
~
j
0
~r
)
~rR
3
r
5
,
~
j
внутр
= 0.
3.25. σ = σ
0
1 − 2πna
3
.
3.26.
J
/
J
0
=
1+∆σ/σ
0
1+∆σ/3σ
0
.
3.27. J =
3πa
2
σ
1
σ
1
+2σ
0
j
0
' 3πa
2
j
0
.
3.28.
J
/
J
0
=
4σ
1
σ
2
(σ
1
+σ
2
)
2
−(σ
1
−σ
2
)
2
a
2
/
b
2
.
3.29. ϕ
1
=
J
0
4πσ
1
1
r
1
+
J
0
4πσ
1
σ
1
−σ
2
σ
1
+σ
2
1
r
2
,
ϕ
2
=
J
0
4πσ
1
2σ
1
σ
1
+σ
2
1
r
1
,
~
j
i
= −σ
i
~
∇ϕ
i
204
ОТВЕТЫ, УКАЗАНИЯ
3.30. j
θ
(θ) =
J sin θ
4πRa
∞
P
n=0
1
n+1
R
a
n
P
0
n
(cos θ) , P
n
(cos θ) - полиномы
Лежандра.
3.31. T = eU −
eJ
v
0
1 + 2 ln b/a − r
2
/a
2
, где v
0
- продольная
скорость электронов.
3.2. Закон трех вторых
3.32. j =
1
9π
q
2e
m
U
3/2
d
2
.
3.33. j =
cU
2πd
2
.
3.34 ∆j ' j
0
p
kT/eU, где j
0
- плотность тока в диоде без учета
тепловых скоростей электронов, которые вылетают из катода, имею-
щего температуру T .
3.35. В четыре раза.
3.36. E
a
=
h
16π
q
mU
2e
je (1 − α)
i
1
/
2
, где α =
j
i
j
e
q
M
m
, j
i
≤ j
e
q
M
m
.
При максимальном токе ионов (α = 1) 1.63≤ j
e
/j
0
≤ 1.97, где j
0
-
плотность тока вакуумного диода, соответствующая закону "3/2".
3.37. j =
9
32π
kU
2
d
3
, где k - подвижность электронов ([k] =
p
см
3
/г).
3.38. J
пог
=
2
9
q
2e
m
U
3/2
a
.
3.39. U (t) = U
0
1 + P
√
U
0
t/2C
2
.
3.40. j
max
= j
0
d
0
2d
2
1 +
U
2
U
1
3/4
2
, где j
0
=
1
9π
q
2e
m
U
3/2
1
d
2
0
- ток
эмиссии плоского диода (ширина d
0
, напряжение U
1
) в дрейфовое
пространство между плоскостями 1,2; x
вирт
=
2d
1+(U
1
/U
2
)
3/4
.
3.41. F
E
/F
M
∼
c
2
v
2
d
2
r
2
≈
d
2
r
2
1.
3.42. J
пред
=
mc
3
e
βγr
d
, где
mc
3
e
' 17kA - параметр Будкера.
3.43. ϕ ∼ ρd
2
' jd
2
c ' J
0
(d/a)
2
.
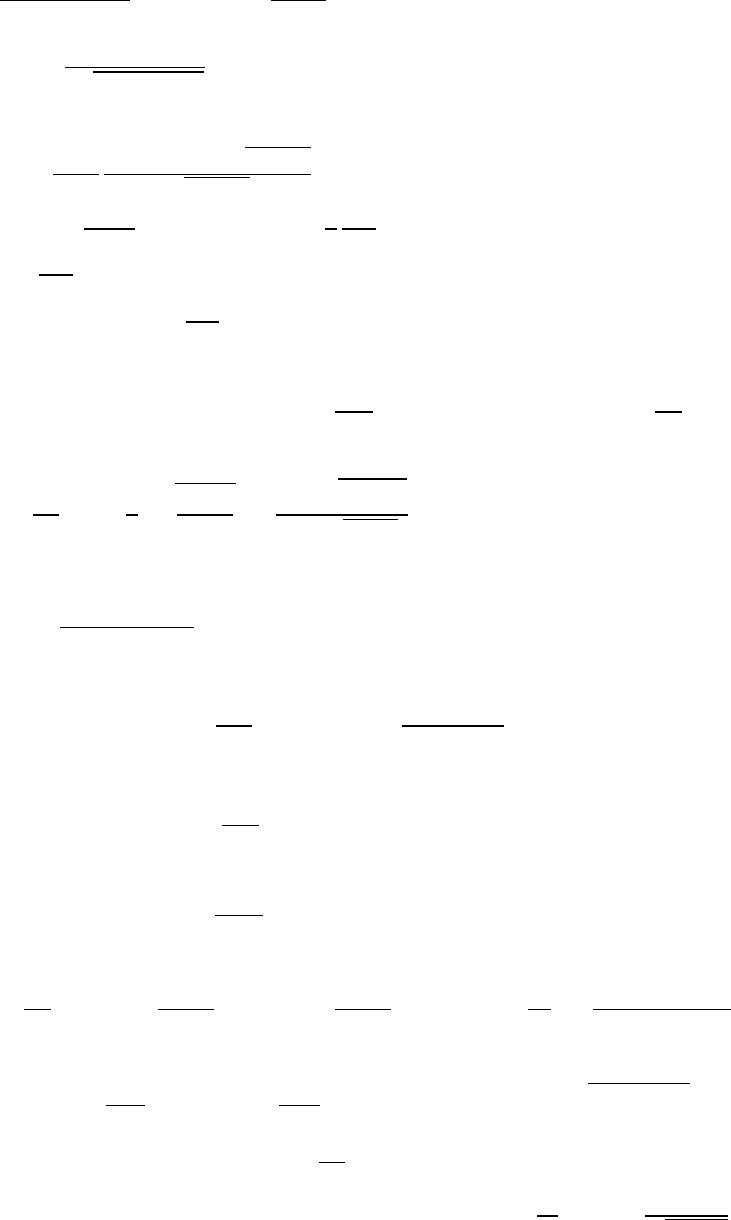
4.1 Закон Био - Савара. Теорема Стокса. Суперпозиция полей
205
4.1. Закон Био - Савара. Теорема Стокса. Суперпозиция полей
4.1. H
z
=
2πJa
2
c
(
a
2
+z
2
)
3/2
. а) H
z
=
2πJn
c
(cos α
1
+ cos α
2
) ,
где α
1,2
= arccos
`∓z
√
a
2
+(`∓z)
2
- углы, под которыми видны края соле-
ноида из точки z; б) H
z
(0) = 2πJn/c; в) H
z
= 4πJn/c.
4.2. H
z
(h) =
2Qω
ca
2
a
2
+2h
2
−2h
√
a
2
+h
2
√
a
2
+h
2
.
4.3. а) H
z
(0) =
πJN
cR
. б) H
z
(0) =
2
3
Qω
cR
.
4.4. а) H =
4πi
c
между плоскостями и H = 0 вне них; б) H = 0
между плоскостями и H =
4πi
c
вне них. В обоих случаях
~
H направлено
вдоль плоскостей и перпендикулярно току.
4.5. H
r
= H
z
= 0 всюду; H
α
=
2Jr
ca
2
при r ≤ a, H
α
=
2J
cr
при
a ≤ r ≤ b и H
α
= 0 при r > b.
4.6. H
0
=
W
ρa
1/2
1
c
q
8πβ
α
2
−1
ln
α+
√
α
2
+β
2
1+
√
1+β
2
, где ρ - удельное сопро-
тивление проводника. H
0
максимально при α = 3 и β = 2; при этом
H
0
[Э] = 0, 179
W [Вт]
ρ[Ом·см]a[см]
1/2
.
4.7. tg α = 2`/4πNa.
4.8. H
x
= H
z
= 0, H
y
=
2πj
c
d, где j =
J
π
(
b
2
−a
2
)
- плотность тока,
ось Y перпендикулярна плоскости, проходящей через оси цилиндров.
4.9. H
x
= H
z
= 0, H
y
=
2πj
c
d, ось Y - перпендикулярна плоско-
сти, проходящей через оси проводников.
4.10 H
z
= H
r
= 0, H
α
=
2JN
cr
, где r - расстояние от вертикальной
оси тора.
4.11. H
x
=
2J
ca
arctg
a+2x
2y
+ arctg
a−2x
2y
, H
y
=
J
ca
ln
(x−a/2)
2
+y
2
(x+a/2)
2
+y
2
,
H
z
= 0; ось Y перпендикулярна полосе и проходит через её середину,
при a x, y, H
x
=
2Jy
cR
2
, H
y
= −
2Jx
cR
2
, H
z
= 0,
R =
p
x
2
+ y
2
.
4.12. H
r
= H
z
= 0 всюду; H
α
=
2J
cr
над плоскостью, H
α
= 0 под
ней. Для полубесконечного тока H
r
= H
z
= 0, H
α
=
J
cr
1 +
z
√
r
2
+z
2
.

206
ОТВЕТЫ, УКАЗАНИЯ
4.13. H
α
=
2J
cr
в воздухе; H
α
=
2J
cr
(1 − cos θ), θ - угол в сфериче-
ской системе координат.
4.14. H
z
(r, z) =
32π
5
√
5
1 − 1, 670
r
2
R
2
− 1, 152
z
4
R
4
J
cR
, где расстоя-
ния r, z отсчитываются от середины отрезка O
1
O
2
поперек и вдоль
него соответственно. Область однородности поля с заданной величи-
ной δ есть цилиндр радиуса r = R
p
δ/1, 67 и длины ` = 2R
4
q
δ
1,152
.
r=0,775 см и `=6,1 см; V = πr
2
`=11,5 см
3
.
4.2. Векторный потенциал, магнитный диполь. Силы действующие на маг-
нитный диполь. Прецессия магнитного момента
4.15 1) Пусть поле
~
H направлено вдоль Z, тогда: а) A
x
= −H ·y,
A
y
= A
z
= 0 или A
x
= −H · y/2, A
y
= H · x/2, H
z
= 0; б) A
r
=
A
z
= 0, A
α
= H · r/2; в) A
r
= A
θ
= 0, A
z
= Hr sin θ/2. 2) Если
ток J течет вдоль оси Z, то A
r
= A
α
= 0 и A
z
= −
2J
c
ln r. 3) Если
ось Z совпадает с осью витка, то A
r
= A
z
= 0 и A
θ
= −
πa
2
Jr
c
(
r
2
+z
2
)
3/2
при a
√
r
2
+ z
2
.
4.16. A
r
= A
α
= 0, A
z
=
J
c
ln
(a+x)
2
+y
2
(a−x)
2
+y
2
; H
x
= −
8J
c
axy
r
2
1
r
2
2
, H
y
=
2J
c
a−x
r
2
1
+
a+x
r
2
2
, H
z
= 0, где r
1
(r
2
) - расстояния до точки наблю-
дения (x, y) в плоскости, перпендикулярной токам, от тока J(−J),
находящегося в точке (a, 0)(−a, 0) соответственно.
4.17.
~
H = −
4πJ
ca
~e
x
+ rot
~
A, где вектор-потенциал
~
A = (0, A
y
, 0);
A
y
=
∞
P
n=1
β
n
e
−2πnz/a
sin
2πnx
a
+ ϕ
n
. Коэффициенты β
n
, ϕ
n
подби-
раются так, чтобы были выполнены граничные условия на поверхно-
сти проводников.
4.18. а) A
r
= A
θ
= 0, A
z
'
4Ja
cr
cos θ или A = 2
[~m×~r]
r
2
, где
~m = 2J [~a~e
z
] - магнитный момент системы (2~a - вектор от тока
−J к току J в плоскости, перпендикулярной токам), r – радиус-
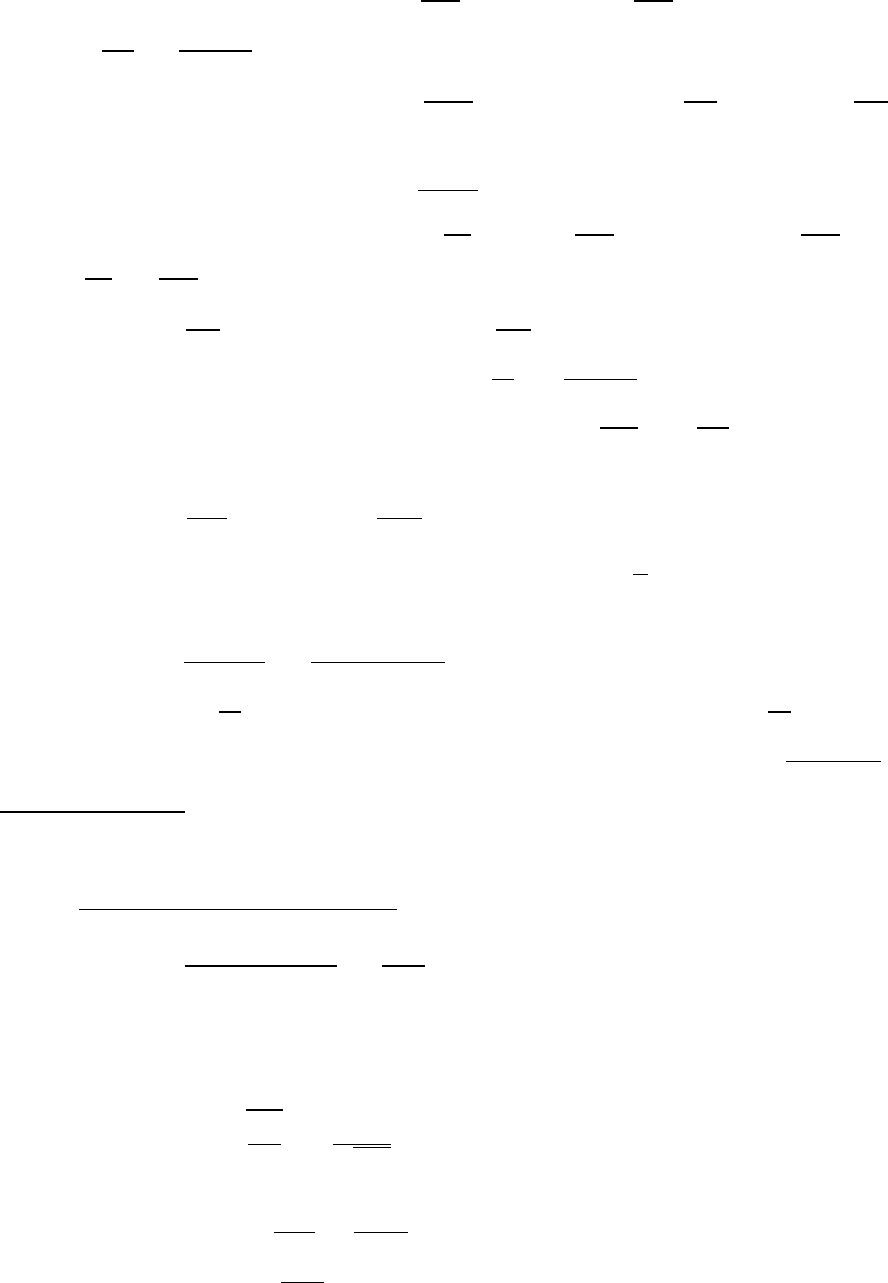
4.2 Векторный потенциал, магнитный диполь. Силы действующие на магнитный диполь. Прецессия магнитного момента
207
вектор точки наблюдения в этой же плоскости из середины рассто-
яния между токами; б) H
r
= −
4Ja
cr
2
sin θ, H
θ
=
4Ja
cr
2
cos θ, H
z
= 0 или
~
H = −
2~m
r
2
+
4(~m~r)~r
r
4
.
4.19. A
x
= A
y
= 0, A
z
=
4Jr
2
ca
2
cos 2α; H
x
=
8J
ca
2
y, H
y
=
8J
ca
2
x,
H
z
= 0.
4.20. A
r
= A
θ
= 0, A
z
= −
2πjaδ
c
ln a.
4.21. A
r
= A
θ
= 0, A
z
= −
2J
c
ln r −
6Ja
cr
cos θ; H
r
=
3Ja
cr
2
sin θ,
H
θ
=
2J
cr
−
6Ja
cr
2
cos θ, H
z
= 0.
4.22. ~m =
ea
2
3c
~ω для сферы и ~m =
ea
2
5c
~ω для шара.
4.23. Вне шара (сферы)
~
H = −
~m
r
3
+
3(~m~r)~r
r
5
, где ~m - магнитный
момент шара (сферы). Внутри сферы
~
H =
2e~ω
3ca
=
2~m
a
3
внутри шара,
где
~
m
∗
- момент шара радиуса r, ~m - момент всего шара.
4.24.
~
H =
q
m
~r
r
3
, где q
m
=
JnS
c
- магнитный заряд соленоида.
4.25.
~
F = 0,
~
N =
h
~m ×
~
H
i
, где ~m =
J
c
R
~nds - магнитный
момент контура.
4.26. U =
(~m
1
~m
2
)
r
3
−
3(~m
1
~r)(~m
2
~r)
r
5
;
~
F
2
= −
~
F
1
=
3
r
5
[~m
2
(~m
1
~r) + ~m
1
(~m
2
~r) + ~r (~m
1
~m
2
)]−
15
r
7
(~m
1
~r) (~m
2
~r) ~r,
где r - радиус-вектор от первого тока ко второму.
~
N
i
=
[~m
2
×~m
1
]
r
3
+
3[~m
i
×~r](~m
i+1
×~r)
r
5
для i = 1, 2 (i + 1 = 2, 1). При параллельных дипо-
лях ( ~m
1
= m
1
~n, ~m
2
= m
2
~n, ~r = r~r
0
, ~n, ~r
0
- единичные векторы),
~
F
2
=
3m
1
m
2
[
2~n(~n~r
0
)−~r
0
(5~n~r
0
)
2
−1
]
r
4
.
4.28. F '
3q
1
q
2
a
2
1
a
2
2
ω
1
ω
2
25c
2
`
4
+
q
1
q
2
`
2
.
4.29. а) h = R
3J
2
π
2
/
8c
2
P
1/4
; б) h = 2πRJ
2
/
c
2
P
.
4.30.
~
F =
~
∇
~m
~
H
.
4.31. v ' H
0
q
a
3
4m
'
H
0
√
4πρ
' 80 м/с, где ρ - плотность материала
шарика.
4.32. F ' 6γβ
2
1−ε
2+ε
2
B
2
a
6
`
4
.
4.33. ~m = g
~
M =
e
2mc
~
M.
208
ОТВЕТЫ, УКАЗАНИЯ
5.1. Граничные условия для магнитного поля. Метод изображений. Постоян-
ные магниты. Магнитные цепи
5.1. Вне сферы H
α
=
2J
cr
, H
z
= H
r
= 0;
~
H = 0 внутри нее.
~
B
i
= µ
i
~
H.
5.2. H
r
= H
z
= B
r
= B
z
= 0 всюду; H
α
= B
α
=
2Jr
ca
2
при r ≤ a,
H
α
=
2J
cr
и B
α
=
2µ
1
J
cr
для z > 0 и B
α
=
2µ
2
J
cr
для z < 0 при r > a.
5.3. B
r
= B
z
= 0 всюду, (B
α
)
i
= µ
i
2J
cr
для i = 1, 2 при a ≤ r ≤ b;
B
α
=
2J
cr
в остальном пространстве.
5.4. B
α
=
2J
cr
2π
(α
1
/µ
1
+α
2
/µ
2
+α
3
/µ
3
)
, H
αi
= B
α
/µ
i
, i = 1, 2, 3.
5.5.
~
H =
1
µ
~
B +
1 −
1
µ
~
B~n
~n, где
~
B - индукция в среде, ~n -
нормаль к щели.
5.6. (A
z
)
внутр
= −
µ
1
Jr
2
ca
2
+
2µ
1
µ
2
µ
1
+µ
2
H
0
r sin α,
(A
z
)
нар
=
2µ
2
J
c
ln
a
r
+
1 +
µ
1
−µ
2
µ
1
+µ
2
a
2
r
2
µ
2
H
0
r sin α; A
r
= A
α
= 0
всюду;
~
H = rot
~
A всюду.
5.7.
~
H
внутр
=
3µ
2
~
H
0
µ
1
+2µ
2
,
~
H
нар
=
~
H
0
−
~m
r
3
+
3(~m~r)~r
r
5
, где m =
µ
1
−µ
2
µ
1
+2µ
2
~
H
0
a
3
- индуцированный магнитный момент, приобретаемый шаром. Плот-
ность объемных токов
~
j
мол
= 0, а поверхностных токов -
i
α
=
3
4π
µ
1
−µ
2
µ
1
+2µ
2
cH
0
sin θ.
5.8.
~
H
внутр
=
3µ
1+2µ
~
H
0
.
5.9.
~
H
внутр
=
3µ
2
µ
1
+2µ
2
~
H
0
−
4π
~
M
0
µ
1
+2µ
2
,
~
H
нар
=
~
H
0
−
~m
r
3
+
3(~m~r)~r
r
5
, где
магнитный момент шара ~m =
µ
1
−µ
2
µ
1
+2µ
2
a
3
~
H
0
+
4π
µ
1
+2µ
2
a
3
~
M
0
.
5.10. H
внутр
= 0,
~
H
нар
=
~
H
0
−
~m
r
3
+
3(~m~r)~r
r
5
, где ~m = −
1
2
a
3
~
H
0
.
Плотность объемных токов
~
j
мол
= 0, а поверхностных – i
α
= −
3
8π
cH
0
sin θ.
5.11.
~
F =
9
64
H
2
a
2
1 +
1
2
sin
2
α
, α – угол между
~
H и нормалью к
плоскости разреза сферы.
5.12.
~
H
внутр
=
4µ
1
µ
2
(µ
1
+µ
2
)
2
−(µ
1
−µ
2
)
2
a
2
/b
2
; при µ
1
µ
2
~
H
внутр
=
4µ
2
/µ
1
1−a
2
/b
2
~
H
0
.
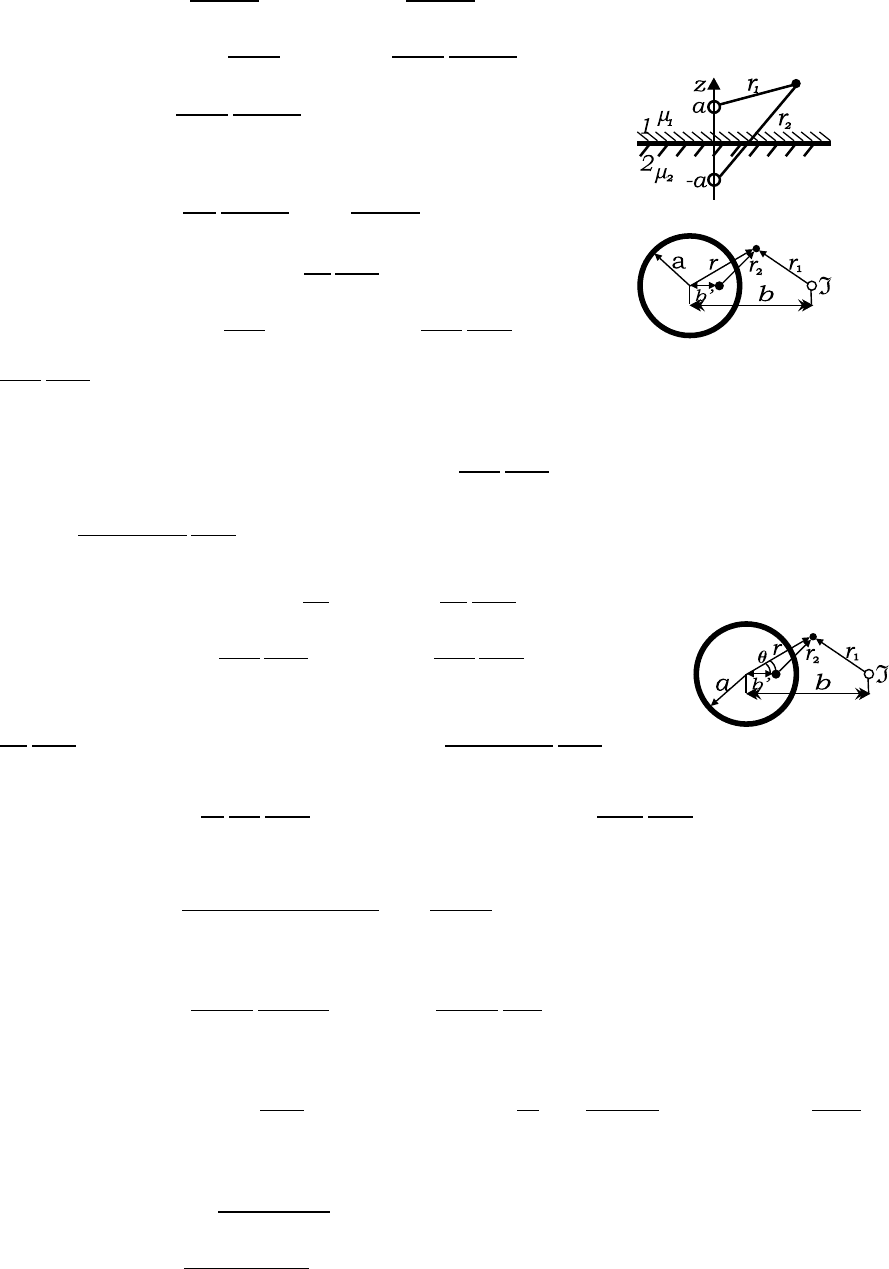
5.1 Граничные условия для магнитного поля. Метод изображений. Постоянные магниты. Магнитные цепи
209
5.13.
~
H
1
=
2µ
2
µ
1
+µ
2
~
H
0
,
~
H
2
=
2µ
1
µ
1
+µ
2
~
H
0
.
5.14. A
1z
= −
2µ
1
J
c
ln r
1
−
2µ
1
J
c
µ
2
−µ
1
µ
1
+µ
2
ln r
2
,
A
2z
= −
2µ
2
J
c
2µ
1
µ
1
+µ
2
ln r
1
,
~
B
i
= rot
~
A
i
=
µ
i
H
i
, i = 1, 2.
5.15. F
z
=
J
1
c
2
a
µ
1
µ
2
µ
1
+µ
2
J
1
µ
1
−µ
2
µ
1
µ
2
+ 4J
2
+ 2J
3
.
5.16. (A
z
)
внутр
= −
2J
c
2µ
1+µ
ln r
1
+ c
1
,
(A
z
)
нар
= −
2µJ
c
ln r
1
= −
2µJ
c
1−µ
1+µ
ln r
2
+
2µJ
c
1−µ
1+µ
ln r + c
2
, где r
2
1
= r
2
+ b
2
− 2br cos θ,
r
2
2
= r
2
+ b
12
−2rb
0
cos θ, b
0
= a
2
b, а c
1
и c
2
связаны соотношением c
1
− c
2
=
2µJ
c
1−µ
1+µ
ln a.
F
r
=
2J
2
a
2
/
b
c
2
(
b
2
−a
2
)
1−µ
1+µ
.
5.17. (A
z
)
внутр
= −
2J
c
ln r
1
+
2J
c
1−µ
1+µ
ln r
2
+ c
1
,
(A
z
)
нар
=
2µJ
c
2
1+µ
ln r
1
+
2µJ
c
1−µ
1+µ
ln r + c
2
,
где r
1
и r
2
те же, что и в 5.16, а c
1
− c
2
=
2J
c
1−µ
1+µ
[(µ − 1) ln a − ln b]. F
r
=
2J
2
a
c
2
(
b
2
−a
2
)
µ−1
µ+1
.
5.18. F
z
=
3
16
m
2
a
4
µ−1
µ+1
1 + cos
2
θ
, N =
m
2
16a
3
µ−1
µ+1
sin 2θ, θ – угол
между ~n и нормалью к границе раздела.
5.19. H =
4πJn
c(d+`
жел
S/µS
жел
)
'
4πJN
cd
.
5.20. H = 4πJN/cb.
5.21. H
1
=
4πJN
c
R
2
−a
2
`R
2
, H
2
=
4πJN
c
a
2
`R
2
.
5.22. H (x) ' H
0
e
−3x/d
.
5.23.
~
H
внутр.
=
8π
µ+2
~
M
0
,
~
H
нар
= −
~m
r
3
+
3(~m~r)~r
r
5
, где ~m =
4πa
3
µ+2
~
M
0
,
~
M
0
– намагниченность магнетика магнита.
5.24. B
max
=
B
0
1+B
0
/2H
0
' 2H
0
= 200 Гс.
5.25. H =
2dH
c
h+2dH
c
/B
1
≈ 1 кГс.
