Меледин Т.В., Черкасский В.С. Электродинамика в задачах. Часть 1. Электродинамика частиц и полей
Подождите немного. Документ загружается.

190
7 ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
7.2. Фокусировка продольным и поперечным полями. Квадрупольные элек-
тростатические и магнитные линзы
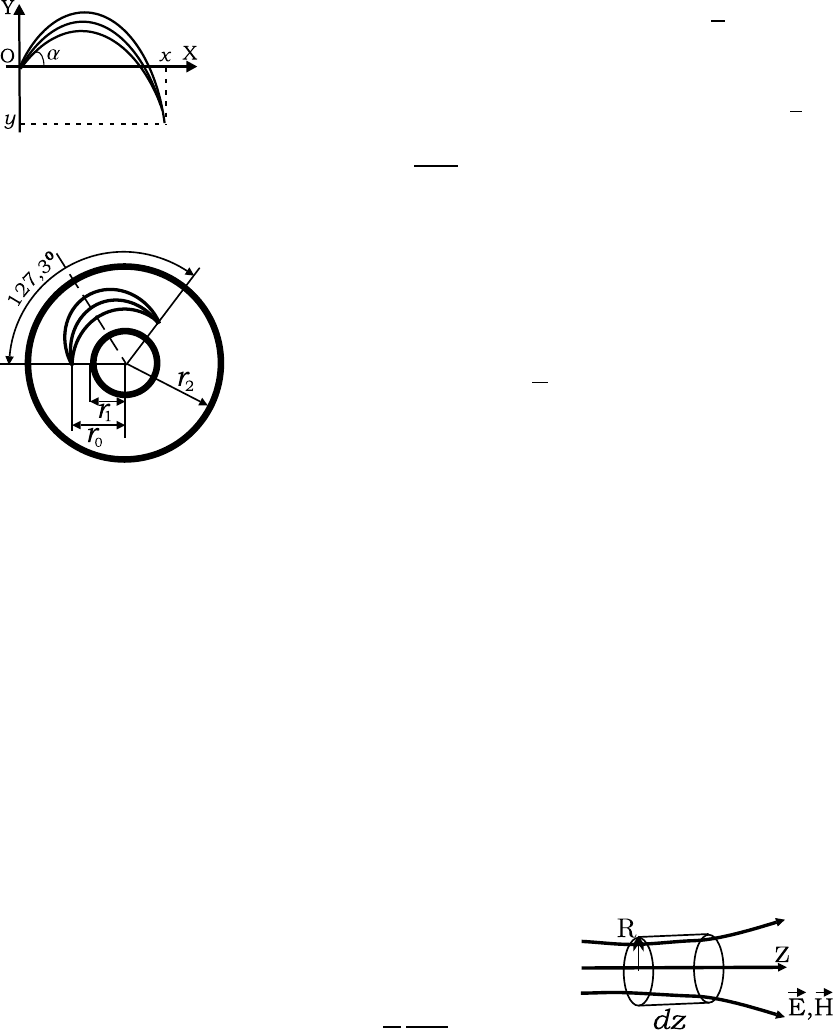
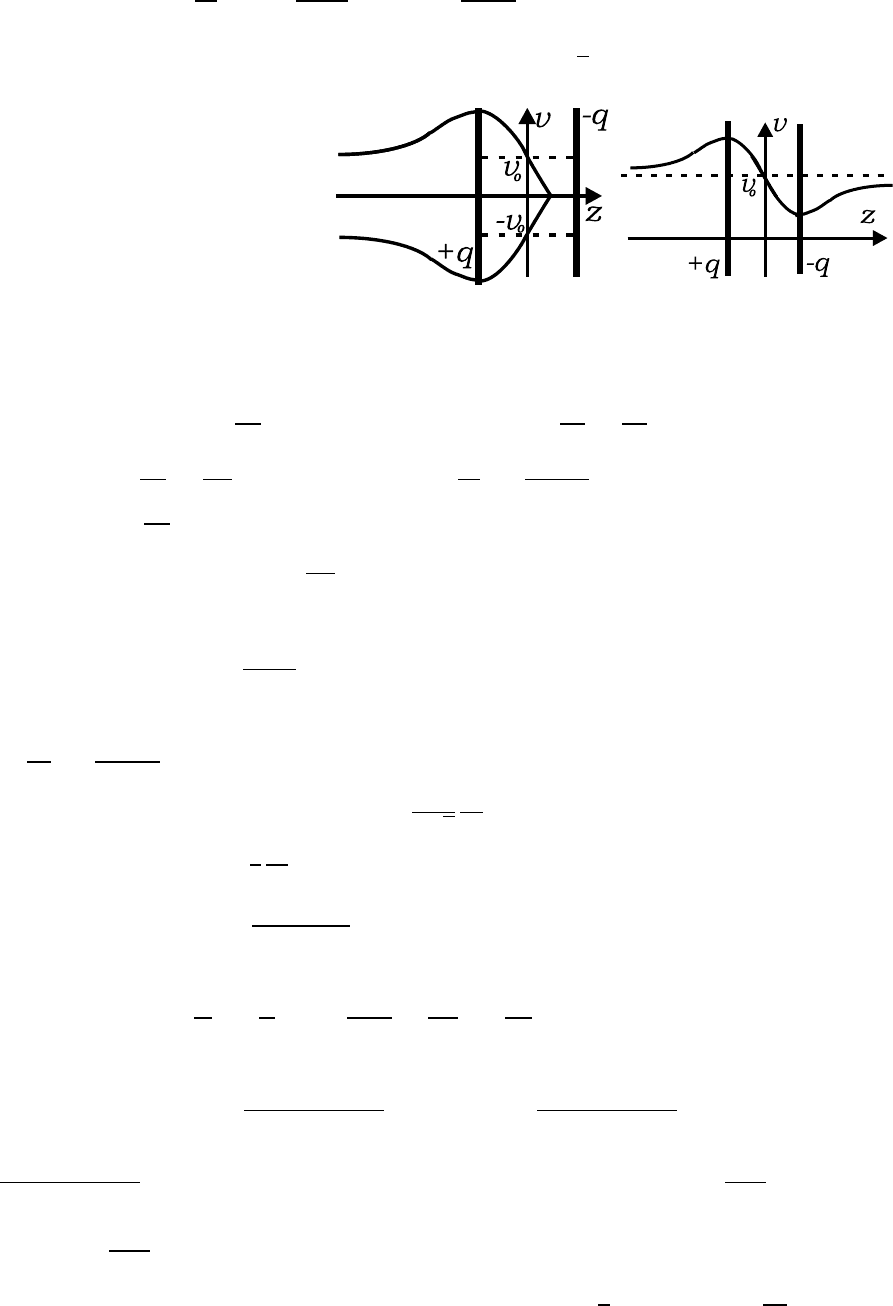
7.11. Показать, что слабо расходящийся пучок заряженных
частиц, испущенных под углом
π
2
+α по направ-
лению к вектору
~
E, фокусируется в точке с ко-
ординатами x = gctgα, y = g
1 −
1
2
sin
2
α
,
где g =
mv
2
0
eE
.
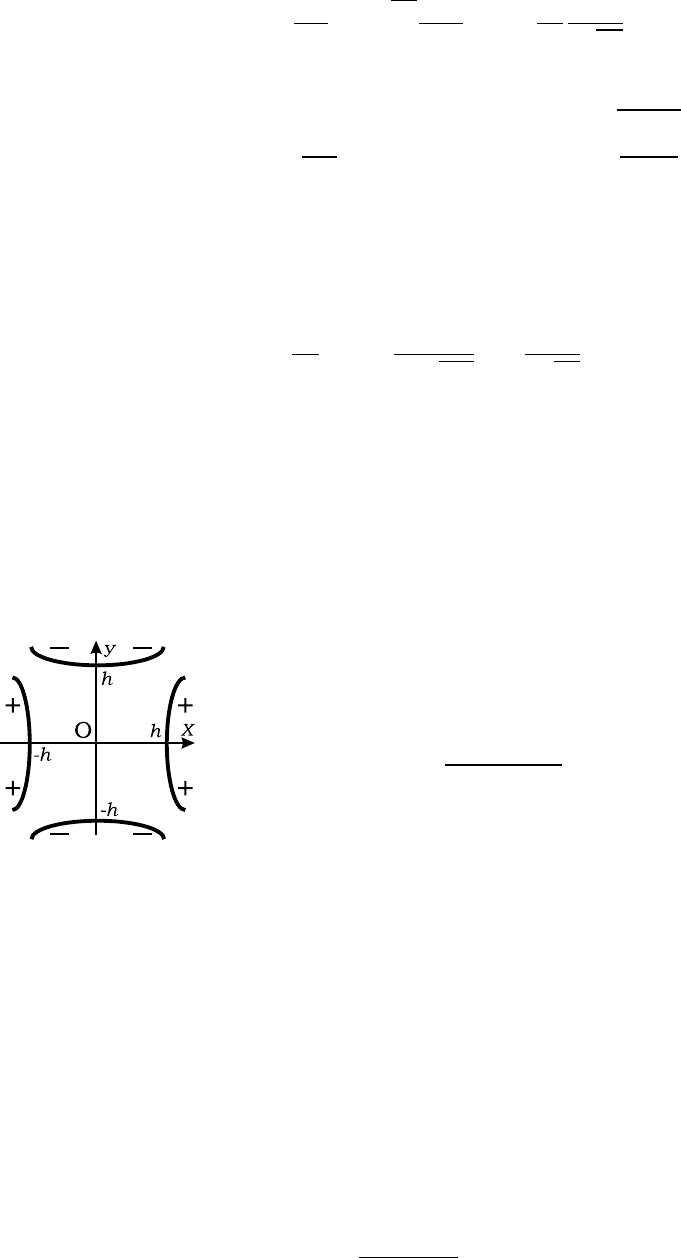
7.12. Показать, что узкий параллельный пучок заряженных
частиц, по касательной входящий в цилиндри-
ческий конденсатор, находящийся под напря-
жением U, будет сфокусирован после поворо-
та на угол π/2
√
2 = 63, 6
o
. Соответственно,
слабо расходящийся пучок сфокусируется по-
сле поворота на угол, вдвое больший. Энергия пучка удовлетворяет
условию mv
2
0
/2 = αq, где α = U/2 ln(r
2
/r
1
).
7.13. На каком расстоянии от точки вылета сфокусируется слабо
расходящийся пучок заряженных частиц движущийся вдоль однород-
ного магнитного поля
~
H. Скорость частиц v, заряд q, масса m.
7.14. На каком расстоянии от точки вылета сфокусируется слабо
расходящийся пучок заряженных частиц, движущийся вначале пер-
пендикулярно магнитному полю
~
H? Скорость частиц v, заряд q, масса
m.
7.15. Используя теорему Гаусса, по-
казать, что в неоднородном аксиально-
симметричном поле E
R
≈ −
R
2
∂E
z
∂z
.
7.16. Показать, что для тонкой электростатической линзы в па-
раксиальном приближении в аксиально симметричном поле уравнение
7.2 Фокусировка продольным и поперечным полями. Квадрупольные электростатические и магнитные линзы
191
траектории заряженной частицы имеет вид
d
dz
√
U
dR
dz
=
R
4
U
00
√
U
причём
v
z
=
dz
dt
= v cos α ≈ v =
r
2qU
m
.
7.17. Показать, что фокусное расстояние F для линзы из задачи
7.16 удовлетворяет соотношению
1
F
= −
1
4
√
U
0
b
Z
a
U
00
√
U
dz,
где U
0
- потенциал вне линзы, а интеграл берется по области поля.
7.18. Показать, что фокусное расстояние F для пучка заряженных
частиц в параксиальном приближении для тонкой электростатической
квадрупольной линзы с потенциалом U = U
0
(x
2
− y
2
)/h
2
удовлетворяет соотношениям
F
−1
x
= p sin p` ≈ p
2
`,
F
−1
y
= −pshp` ≈ −p
2
`,
где p =
p
qU/mv
2
0
/h.
7.19. Показать, что для системы двух последовательных квадру-
полъных линз, расположенных на расстоянии d, имеющих фокусные
расстояния F
x
= F , F
y
= −F и повёрнутых в плоскостяхXY друг
относительно друга на 90
o
, результирующие фокусные расстояния по
осям X и Y одинаковы и равны ∼ F
2
/d при d F .
7.20. Показать, используя проекции уравнения движения в акси-
ально симметричном магнитном поле и результат задачи 7.15, что для
частиц с зарядом e и массой m, разогнанных предварительно напря-
жением U, фокусное расстояние тонкой магнитной линзы равно:
F =
e
8mc
2
U
Z
H
2
z
dz
−1
.

192
7 ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОЛЯХ
7.21. Показать, что для пучка заряженных частиц фокусные рас-
стояния в параксиальном приближении для магнитной квадруполь-
ной линзы с магнитным скалярным потенциалом ϕ
m
= −bxy равны:
F
x
= (p sin p`)
−1
, F
y
= −(p sh p`)
−1
, где p =
q
qb
mv
0
c
.
7.22. Параллельно оси сплошного проводящего (литиевого) цилин-
дра, по которому течёт ток J = 0, 5 МА, пролетает ультрареляти-
вистский протон с энергией E = 300 ГэВ. Длина цилиндра ` = 10
см, радиус R = 1 см. Найти фокусное расстояние такой линзы. По-
казать, что при указанных условиях линза тонкая. Энергия покоя про-
тона E
0
= m
p
c
2
= 1 ГэВ.
ОТВЕТЫ, УКАЗАНИЯ
193
ОТВЕТЫ, УКАЗАНИЯ
1.1. Закон Кулона. Поле и потенциал точечного заряда. Принцип суперпози-
ции.
1.1. r
min
=
e
2
E/2
; T '
e
2
2r
min
k
' 3, 35 ·10
10
K.
1.2. v
поз
=
e
2
/a
m
4
√
2+1
√
2
1/2
, v
прот
=
e
2
/a
M
1
√
2
1/2
.
1.3. v =
h
q
2
/a
m
√
3 − 1
i
1/2
, E
ион
=
3
2
√
3 − 1
q
2
a
.
1.4.v =
2q
ma
1/2
√
q
2
−
√
q
1
при q
1
< q
2
; v = 0 при q
2
< q
1
.
1.5. Q
нов
= k
1
k
2
Q.
1.6. E
α
=
U/α
0
r
, E
r
= E
z
= 0.
1.7. q
1,2
=
R
√
R
2
+a
2
qa
2
A
1,2
√
R
2
+ a
2
− A
2,1
R
.
1.8. ∆T =
1
8
mv
2
C
mv
2
e
2
/R
.
1.9. ϕ = ϕ
0
/2; поле не изменится по величине, вектор поля повер-
нется на угол π/3 и станет направленным перпендикулярно оставшей-
ся палочке.
1.10. Сфера радиуса R =
a
q
1
q
2
q
2
1
−q
2
2
с центром на линии, проходящей
через заряды на расстоянии x
1
= a
q
2
1
q
2
1
−q
2
2
от заряда q
1
в сторону заряда
q
2
. При этом x
1
= R |q
1
/q
2
| и |x
1
(a − x
1
)| = R
2
.
1.11. а) ϕ = q/`; б) Q = −qR/`.
1.12 ϕ =
q
(
a
2
+h
2
)
1/2
, E
z
=
qh
(
a
2
+h
2
)
3/2
.
1.13. Внутри сферы E
z
=
2πσR
2
a
2
1 −
R
√
a
2
+R
2
. Над полусферой с
плотностью 2σ E
z
=
2πσR
2
a
2
3 +
R
√
a
2
+R
2
. Под полусферой с плот-
ностью σ E
z
= −
2πσR
2
a
2
3 −
R
√
a
2
+R
2
.
1.14. ϕ
нар
= 2πσR
2
a, ϕ
внутр
= 2πσR.
1.15. а)ϕ
отв
= −2πσ
√
R
2
+ z
2
, E
z отв
=
2πσz
√
R
2
+z
2
;
194
ОТВЕТЫ, УКАЗАНИЯ
б) ϕ
диск
= 2πσ
√
R
2
+ z
2
− |z|
, E
z диск
= 2πσz
1
|z|
−
1
√
R
2
+z
2
;
в) ϕ
плоск
= −2πσ |z|, E
z плоск
= 2πσ
z
|z|
.
1.16. E
z
(O
1
) = E
z
(O
2
) =
−2πσd
√
a
2
+d
2
, E
z
(O
3
) = −
2πσd
√
a
2
+d
2
/4
.
1.17.
~
E = 0.
1.18. P =
Q
2
8πR
4
.
1.2. Теорема Гаусса
1.19. а)
~
E = 2πσ~z/|z|; б) внутри конденсатора |E| = 4πq/S, вне
~
E = 0; в)
~
E =
2κ
r
2
~r.
1.20. Направление сил
показано на рисунке.
E
+
=
2κ
a
, E
−
=
2κ
a
√
3.
1.21. E
2n
−E
1n
= 4πσ, где внешняя нормаль ~n к поверхности раз-
дела направлена из среды 1 в среду 2.
∂ϕ
1
∂n
−
∂ϕ
2
∂n
= 4πσ.
1.23. а)
~
E
внутр
=
4
3
πρ~r (r ≤ a) ;
~
E
нар
=
4
3
πρ
a
r
3
~r (r ≥ a);
б)
~
E
внутр
=
2κ
a
2
~r (r ≤ a) ;
~
E
нар
=
2κ
r
2
~r (r ≥ a) ;
в)
~
E
внутр
= 2πσ
~z
a
(|z| ≤ a) ,
~
E
нар
= 2πσ
~z
|z|
(|z| ≥ a).
1.24.
~
E =
4
3
πρ~a, где ~a - вектор из центра шара в центр полости.
1.25. σ
0
1
= σ
0
2
=
1
2
(σ
1
+ σ
2
) , σ
00
1
= −σ
00
2
=
1
2
(σ
1
− σ
2
) .
1.26. q =
4πα
3−n
R
3−n
2
− R
3−n
1
для n 6= 3; q = 4πα ln
R
2
R
1
для
n = 3.
~
E = 0 при r ≤ R
1
,
~
E =
q~r
r
3
при r ≥ R
2
,
~
E =
q~r
r
3
(r/R
1
)
3−n
−1
(R
2
/R
1
)
3−n
−1
для n 6= 3 и
~
E =
q~r
r
3
ln(r/R
1
)
ln(R
2
/R
1
)
для n = 3 при R
1
≤ r ≤ R
2
.
1.3. Диполь. Мультиполи
1.27. ϕ =
~p~r
r
3
,
~
E = −
~p
r
3
+
3(~p~r)~r
r
5
; вектор ~p направлен от −q к +q.
1.3 Диполь. Мультиполи
195
1.28.
~
F = q
~p
r
3
− 3q
(~p~r)~r
r
5
,
~
N = q
[~r×~p]
r
3
.
1.29.
~
F =
~
∇
~p
~
E
; при ~p ∼
~
E,
~
F =
1
2
~
∇
~p
~
E
.
1.30. v(0) = v
0
1.31. r = C sin
2
θ.
1.32. б) ~a = −
P
i
q
i
~r
i
/
P
i
q
i
.
1.33. ϕ
внутр
=
4π
3
σ
0
r cos θ,
~
E
внутр
= −
4π
3
σ
0
~z
|z|
;
ϕ
нар
=
4π
3
σ
0
R
3
r
2
cos θ,
~
E
нар
= −
~p
r
3
+
3(~p~r)~r
r
5
,
где ~p =
4π
3
σ
0
R
3
~e
z
.
1.34. ϕ (r, θ) = 2πσ
R
3
r
2
cos θ.
1.35.
~
E = 8σ~e
y
.
1.36. ϕ (~r) =
2(~p~r)
r
2
, где ~p = κ~a, ~a - вектор от нити с зарядом
−κ к нити с зарядом +κ в плоскости, перпендикулярной нитям.
~
E =
−
2~p
r
2
+
4(~p~r)~r
r
4
.
1.37. ϕ (r, θ) ' −6κ ln r +
2
3
√
3
a
3
r
3
κ cos 3α.
1.38. ϕ (r, θ) =
3
4
Q
r
3
3 cos
2
θ − 1
.
1.39. ϕ (r, θ) '
q
(
b
2
−a
2
)
4r
3
3 cos
2
θ − 1
при r a, b;
ϕ (r, θ) ' q
1
a
−
1
b
−
qr
2
4
1
a
3
−
1
b
3
3 cos
2
θ − 1
(r a, b) .
1.40. ϕ (~r) '
4qRx
π
(
R
2
+z
2
)
3/2
; E
x
= −
4qR
π
(
R
2
+z
2
)
3/2
, E
y
= 0, E
z
=
12qRxz
π
(
R
2
+z
2
)
5/2
вблизи оси кольца. При |z| R ϕ (~r) =
(~p~r)
r
3
,
где ~p =
4qR
π
~e
x
; ϕ(~r) – потенциал поля диполя.
1.41. Q = πa
2
σ, ~p = Q
~
h,Q
xx
= Q
yy
= −
1
2
Q
zz
= Q
a
2
4
− h
2
.
196
ОТВЕТЫ, УКАЗАНИЯ
1.42. а) ϕ (r, θ) '
qa
2
r
3
3 cos
2
θ − 1
; б) ϕ (r, θ) '
3qa
2
2r
3
sin
2
θ sin 2α.
1.43. r = c
p
sin
2
θ · |cos θ|.
1.44. ϕ (r, θ) '
3qa
3
r
4
5 cos
2
θ − 3
cos θ.
1.45. ϕ '
q
r
a
r
n
.
1.4. Уравнения Пуассона и Лапласа
1.46. ρ(r) = qδ (r) −
q
4πa
2
e
−r/a
r
.
1.47. а) ϕ
внутр
=
2
3
πρ
3R
2
− r
2
; ϕ
нар
=
4πR
3
3
ρ
r
;
б) ϕ
внутр
= κ
1 −
r
2
R
2
, ϕ
нар
= −2κ ln
r
/
R
;
в) ϕ
внутр
= −2πρz
2
, ϕ
нар
= 2πρa (a −2 |z|) .
1.48.
~
E = −
U
ln R
2
/R
1
~r
r
2
.
1.49. ϕ (x, y, z) =
2πσ
0
γ
e
−γ|z|
sin αx · sin βy, γ =
p
α
2
+ β
2
.
1.50. а) ϕ =
e
r
1 +
r
a
e
−r/a
; б) E
r
=
e
r
2
1 + 2
r
a
+ 2
r
2
a
2
e
−2r/a
;
в) W = −
e
2
a
.
1.51.
~
E
внутр
= 0,
~
E
нар
=
~
E
0
−
~
P
r
3
+
3
(
~
P~r
)
~r
r
5
, где
~
P =
~
E
0
R
3
; σ =
3
4π
E
0
cos θ.
1.53. Пусть a, b, c – длины ребер параллелепипеда вдоль осей X, Y, Z
соответственно и грань z = c имеет потенциал U. Тогда ϕ (x, y, z) =
∞
P
m,n=1
A
nm
sin α
n
x ·sin β
m
y ·sh γ
nm
z, где α
n
=
πn
a
, β
m
=
πm
b
, γ
nm
=
p
α
2
n
+ β
2
m
, A
nm
=
16U
π
2
nm sh(γ
nm
c)
для одновременно нечетных n и m,
A
nm
= 0 в остальных случаях.
2.1. Граничные условия
2.1. ε
2
E
2n
− ε
1
E
1n
= 4πσ, где внешняя нормаль ~n к поверхности
раздела направлена из среды 1 в среду 2. E
1τ
= E
2τ
.
2.2. E
2n
− E
1n
=
ε
1
ε
2
− 1
E
1n
=
1 −
ε
2
ε
1
E
2n
;
σ
1связ
= P
1n
=
ε
1
−1
4π
E
1n
, σ
2связ
= −P
2n
=
1−ε
2
4π
E
2n
.
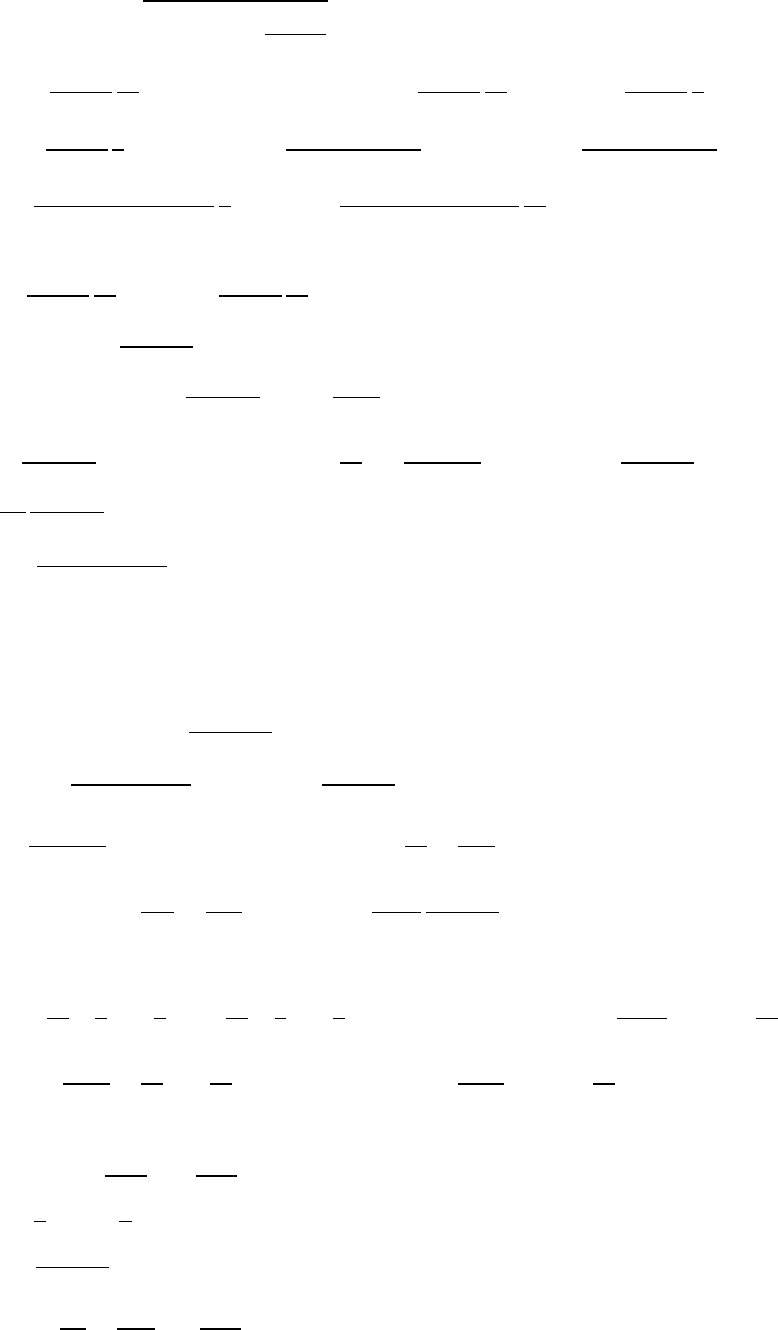
2.2 Емкость
197
2.3. |
~
F | = q|
~
E
0
|
q
sin
2
α +
cos
2
α
ε
2
.
2.4.
~
E
1,2
=
2q
ε
1
+ε
2
~r
r
3
,
~
D
1,2
= ε
1,2
~
E
1,2
=
2ε
1,2
ε
1
+ε
2
~r
r
3
, ϕ
1,2
=
2q
ε
1
+ε
2
1
r
.
2.5. ϕ
1,2
=
2q
ε
1
+ε
2
1
r
, σ
1,2своб
=
qε
1,2
2πR
2
(ε
1
+ε
2
)
, σ
1,2связ
=
q(1−ε
1,2
)
2πR
2
(ε
1
+ε
2
)
.
2.6. ϕ
i
=
2πq
ε
1
α
1
+ε
2
α
2
+ε
3
α
3
1
r
,
~
E
i
=
2πq
ε
1
α
1
+ε
2
α
2
+ε
3
α
3
~r
r
3
,
~
D
i
= ε
i
~
E
i
, где
i = 1, 2, 3.
2.7.
~
E
i
=
4κ
ε
1
+ε
2
~r
r
2
,
~
D
i
=
4κε
i
ε
1
+ε
2
~r
r
2
, где i = 1, 2.
2.8а. ϕ
внутр
= −
3ε
2
ε
1
+2ε
2
E
0
r cos θ,
ϕ
нар
= −E
0
r cos θ +
ε
1
−ε
2
ε
1
+2ε
2
E
0
a
3
cos θ
r
2
;
~
E
внутр
=
3ε
2
ε
1
+2ε
2
~
E
0
,
~
E
нар
=
~
E
0
−
~
P
r
3
+
3
(
~
P~r
)
~r
r
5
, где
~
P =
ε
1
−ε
2
ε
1
+2ε
2
~
E
0
a
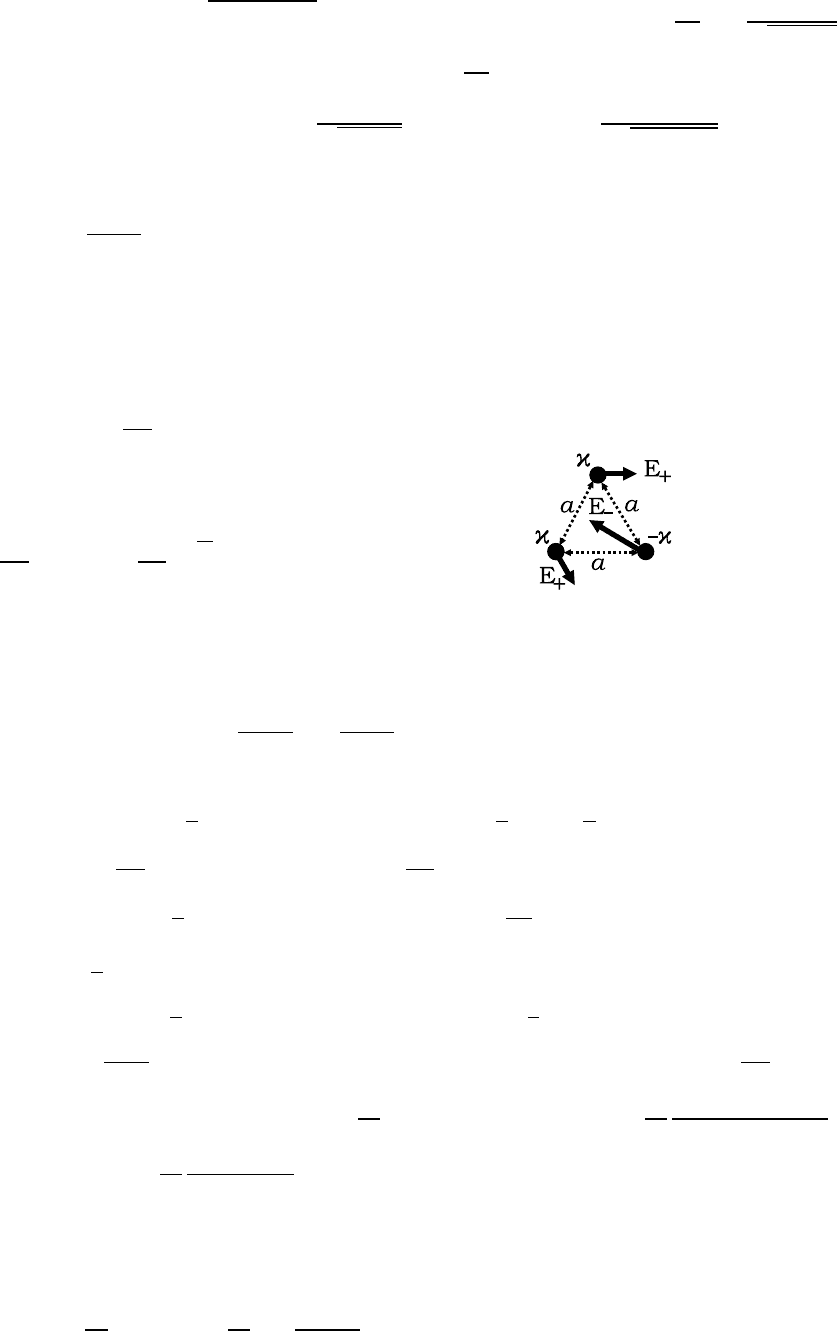
3
;
σ
связ
=
3
4π
ε
1
−ε
2
ε
1
+2ε
2
E
0
cos θ.
2.8б.
~
E =
9ε
(1+2ε)(2+ε)
~
E
0
.
2.2. Емкость
2.9. C ' 20 см (C '
h
2 ln h/R
, где h ' рост, 2πR ' талия).
2.10. а) C '
`
2(π+ln `/a)
; б) C '
`
2 ln `/a
.
2.11. C =
ε
0
S
4πa ln 2
, σ
связ
|
ϕ=0
= −
1 −
1
ε
0
CU
S
;
σ
связ
|
ϕ=U
=
1 −
1
2ε
0
CU
S
, ρ
связ
=
CUa
ε
0
S
1
(x+a)
2
.
2.12. U = 4πn
0
hd
0
.
2.13. C =
h
1
ε
1
1
a
−
1
c
+
1
ε
2
1
c
−
1
b
i
−1
; σ
связ
(a) = −
q
4πa
2
1 −
1
ε
1
,
σ
связ
(c) =
q
4πc
2
1
ε
2
−
1
ε
1
, σ
связ
(b) =
q
4πb
2
1 −
1
ε
2
, где q –
заряд внутренней обкладки.
2.14. C =
1 +
ε−1
4π
Ω
ab
b−a
.
2.15. C '
a
2
(1 +
a
b
).
2.16. C '
1
4 ln b/a
.
2.17. Q = −
S
4π
U
1
`−b
+
U
2
b−a
.
198
ОТВЕТЫ, УКАЗАНИЯ
2.18. q
B
=
SU
4π
1
d
1
+
1
d
2
, q
A
=
1
2
q −
SU
2πd
1
, q
C
=
1
2
q −
SU
2πd
2
.
2.19. Q = −Uhr/d.
2.20. Q = −UC
2
(R
1
+R
2
)C
1
+R
2
C
3
(R
1
+R
2
)(C
1
+C
2
+C
3
)
.
2.21. q
0
i
= q
i
− ¯q, где ¯q =
1
3
(q
1
+ q
2
+ q
3
).
2.3. Метод изображений
2.22. ϕ
1
=
q
r
+
−
q
r
−
, ϕ
2
= 0,
~
E
1
= −
~
∇ϕ
1
,
~
E
2
= 0;
σ
инд
= −
aq
2π
(
a
2
+R
2
)
3/2
, q = −q; F
z
= −
q
2
4a
2
.
2.23. F
x
= −
κ
2
a
, σ (y) = −
κa
π
(
a
2
+y
2
)
.
2.24. Поле внутри двугранного угла создается системой зарядов,
изображенных на соответствующем рисунке:
2.25. ϕ (0) =
Q
(
√
R
2
+4h
2
−R
)
R
√
R
2
+4h
2
, E
z
(0) = −
2Qh
(
R
2
+4h
2
)
3/2
.
2.26. F =
∞
P
i=0
8q
2
ad(2i+1)
[
(2i+1)
2
d
2
−4a
2
]
2
'
8q
2
a
d
3
∞
P
i=0
1
(2i+1)
3
'
8q
2
a
d
3
.
2.27. а) Заряд внутри, сфера заземлена:
ϕ
внутр
=
q
r
+
q
0
r
0
, ϕ
нар
= 0; σ
инд
(r
∗
) = −
q
(
a
2
−`
2
)
4πar
∗3
,
q
инд
=
R
сф
σdS = −q.
б) Заряд внутри, сфера изолирована: ϕ
внутр
=

2.3 Метод изображений
199
q
r
+
q
0
r
0
+
q
a
; ϕ
нар
= 0; σ
инд
(r
∗
) =
q
4πa
2
−
q
(
a
2
−`
2
)
4πar
∗3
, q
инд
= 0.
в) Заряд снаружи, сфера заземлена:
ϕ
нар
=
q
r
+
q
0
r
0
, ϕ
внутр
= 0, σ
инд
(r
∗
) = −
q
(
a
2
−l
2
)
4πar
∗3
,
q
инд
= −q
a
`
.
г) Заряд снаружи, сфера изолирована:
ϕ
нар
=
q
r
+
q
0
r
0
−
q
0
r
0
, ϕ
внутр
= −
q
0
a
; σ
инд
(r
∗
) = −
q
0
4πa
2
−
q
(
a
2
−`
2
)
4πar
∗3
,
q
инд
= 0. Во всех случаях `
0
= a
2
`, q
0
= −qa/`
0
. F = −
q
2
a`
(
`
2
−a
2
)
2
.
2 28. U =
Qq
`
−
q
2
a
3
2`
2
(
`
2
−a
2
)
, F =
Qq
`
2
−
q
2
a
3
(
2`
2
−a
2
)
`
3
(
`
2
−a
2
)
2
;
Q =
qa
3
(
2`
2
−a
2
)
`
(
`
2
−a
2
)
2
.
2.29. F =
q
0
q
`
2
+
q
2
a
`
3
−
q
2
a`
(
`
2
−a
2
)
2
.
2.30. а) ϕ
нар
=
(
~
P
0
~
R
)
R
3
+
(
~
P~r
)
r
3
, где диполь изображения
~
P = −
~
P
0
a
3
`
3
расположен на линии, соединяющей диполь
~
P
0
с центром сферы, на
расстоянии a
2
/` от него; векторы
~
R и ~r отсчитываются от диполя
~
P
0
и его изображения
~
P соответственно; ϕ
внутр
= 0;
б) σ = −
3P
0
4πa
3
cos θ, где θ - угол между
~
P
0
и направлением из центра
сферы в точку на её поверхности.
2.31. ϕ = 2πκ −
2πκ`a
√
h
2
+`
2
√
`
02
+(h
0
−h)
2
, где `
0
=
a
2
`
h
2
+`
2
- радиус кольца
изображения, расположенного на расстоянии h
0
=
a
2
h
h
2
+`
2
от центра
полости. E
z
= −
2πκa`
(
h
0
−h
)
√
h
2
+`
2
[
`
02
+(h
0
−h)
2
]
3/2
.
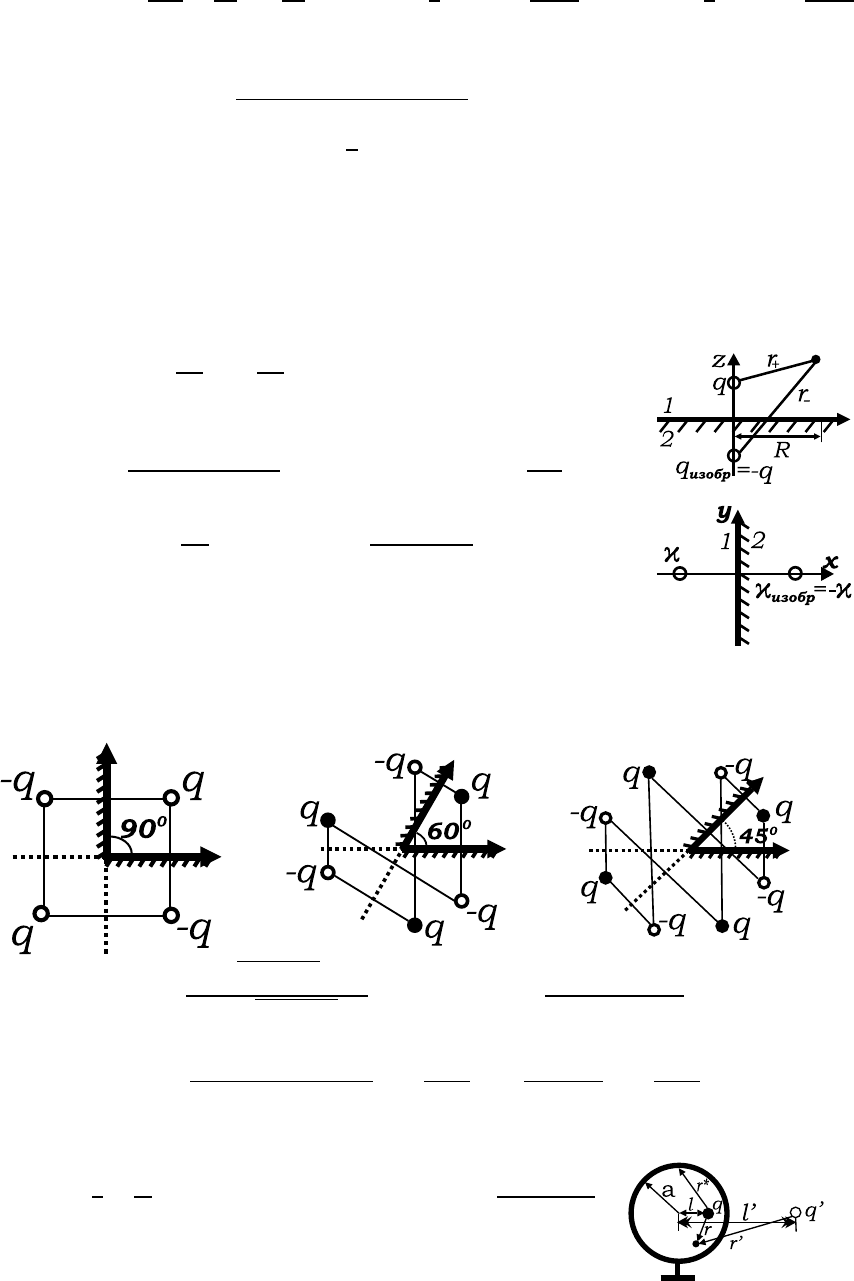
2.32. ϕ = q/r
1
− q/r
2
+ q
0
/r
3
− q
0
/r
4
,
где q
0
= −q
a
b
, b
0
=
a
2
b
; r
i
показаны на рисунке
и Q
инд
= −q
1 −
b
2
−a
2
b
√
b
2
+a
2
.
2.33. σ
плоск
инд
(ρ) = −
E
0
4π
1 −
a
3
ρ
3
; σ
вздут
инд
(θ) =
−
3E
0
4π
cos θ; F
z
=
9
16
a
2
E
2
0
.
