Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

2 Modeling of the Thermophysical Processes in FKNME 

cos

kk l k

HA A V

γγ

εσ

−

∫∫

•• • (2.43)

By defining the direct exchanging area

sg , which represents the overall

influence resulting from geometry and physical properties:

cos

rk l k

gs A V

−

∫∫

˙ •• • (2.44)

We simplify Eq.2.43 into:

γγ

TSgAH

krkk

−

(2.45)

The above equation reveals that the heat flux from

V to

A is the production

of the black body radiation and the direct exchanging area.

The total heat flux towards

A from all N volume elements should be:

∑

TSg

γγ

(2.46)

On the other hand, all of the

M gray diffusive surface elements with area

A (j=

1, …,

M) radiate to

A :

cos cos d d

jk k l

θθ

−

∫∫

•••

(2.47)

where

J is the effective radiation of

A . Eq.2.47 can be expressed in a way

similar to Eq. 2.45:

kk jki

HASSJ˙•

(2.48)

where

SS is the direct exchanging area between the surfaces j and k with

definition out of Eq.2.47:

cos cos d d

jk l

θθ

−

∫∫

•••

(2.49)

The total heat flux from the

M surface elements towards the surface element

A is then:

∑

ikj

JSS

(2.50)

The big total of the heat flux towards

A is obtained by summarizing

contributions from both surfaces and bodies:

⎟

⎠

⎞

⎜

⎝

⎛

+=+=

∑∑

ikjkr

jkkk

JSSTSg

HHH



γγ

(2.51)

As the effective radiation from

A is:

4

)1(

kkkkk

HTJ

εσε

−+= (2.52)

The difference between incoming and outgoing radiation flux is:

  Ping Zhou, Feng Mei and Hui Cai

4

kkkkkkk

HTHJq

εσε

−=−= (2.53)

In case of unknown gases temperature

, another N equations are needed to

close the equations set. The following energy balance equation can be used to

describe the relationship among volume elements.

−

∗

∗∗

∑

∫∫

γγ

γγγ

σε

π4

cos

∗

−

∑

∫∫

∑

∗

−

∗

γγ

σε

cos

∑

∫∫

−

(2.54)

Define

gs as the direct exchanging area from a surface to a gaseous volume:

cos

∫∫

−

(2.55)

Knowing from Eq.2.44 that the direct exchanging area from a surface to a

gaseous volume should be identical to that from a gaseous volume to a surface,

namely:

krrk

sggs = (2.56)

Similar relationships exist for gases to gases and surface to surface:

ijji

ssss = ;

ijji

gggg =

The direct exchanging area between gaseous volumes

γγ

∗

is defined as:

γγ

∗

−

∫∫

(2.57)

Substituting all above definitions and relationships into Eq.2.54 leads to

sgJggTVT

∑∑

∗

γγ

γγγ

σσε

(2.58)

With the help of Eq.2.58, N energy balance equations can be established for

N gaseous volumes. Therefore the temperatures fields and the heat fluxes

among the elements in any enclosure can be determined by the following

procedure:

a) Determining the direct exchange areas of the involved elements.

b) Resolving M

ˇN heat balance equations for temperatures in the M surface

elements and N gaseous volume elements.

c) Determining the difference in fluxes balance of the M surface elements as

2 Modeling of the Thermophysical Processes in FKNME 

well as the total heat exchange in the system.

Obviously the accuracy of the zone method chiefly depends on how to define

the zones and how many zones to be defined. Larger number of zones helps to

improve accuracy but also exponentially raises the computational load. Automatic

zone partition becomes difficult if the geometry is complicated. Basically the zone

method requires large amount of human intervention for high computational

efficiency and accuracy. It has also been found that serious inconsistency between

the defined radiation zones and the mesh grids setup can also bring substantial

difficulties to numerical resolving process when applying finite element or finite

difference method.

2.2.3



Monte Carlo method

The Monte Carlo method is a computational algorithm, which relies on repeated

random sampling to simulate physical processes. In the case of simulating a

radiation process, a number of rays of radiation are sampled and simulated along

the entire process from emitting, traveling in and interacting with the medium to

finally arriving on a surface and being absorbed or reflected. So long as the

number of sampled radiation rays is sufficiently large (more than 100,000) the

Monte Carlo method may satisfyingly predict the overall heat transfer process.

The disadvantage of the Monte Carlo method is the demanding need to the

computational capacity. A relatively simple problem may also require large

amount of computation.

Assuming the elementary volume

V emits N rays with ω Joule energy in

each ray. These rays are “emitted” following the directions randomly decided by

the random cumulative probability function R

(Siegel and Howell, 1990; Zhu,

1989) .

sin

= (2.59)

We assume the ray concerned goes in a randomly determined direction

and is

absorbed after traveling over a distance of

l. The energy intensity of the ray should

be reduced to e

-αs

after traveling over a distance of s in a medium with constant

absorptivity. The probability function

()

sp represents the probability of this ray

traveling over a distance

s before it is entirely absorbed.

()

−

∞

−

∫

Adopting the cumulative probability function

()

sspR

−

−==

∫

e1d

  Ping Zhou, Feng Mei and Hui Cai

Rl −−= 1ln(

The above expression can be equivalently written as

Rl ln

−= because R

a random value uniformly distributed between 0 and 1.

Under thermal equilibrium condition, the medium emits an identical number of

rays after having absorbed a certain quantity of radiation rays. The emission

direction (

) over a sphere around the medium is determined by a cumulative

probability function

()

R21cos

−=

(2.60)

Together with

, the emission direction given by Eq.2.60 determines where this

ray will be absorbed.

This emitting

üabsorbingüemitting (diffusion) process is repeated until the ray

reaches its destination. We then may move on for the next ray until all of the

rays have been “emitted”. The number of the rays that have been absorbed by the

surfaces or the gaseous volumes will be then recorded.

Under thermal equilibrium condition, the energy radiated by a medium volume

should equal to the energy it absorbs. Giving

as the number of absorbed rays

by the medium finite volume d

v and

as the energy contained in each ray, we

have

vTS

vpv

σαω

=⋅ (2.61)

where

is the Planck mean absorptivity. The average temperature in the finite

volume is then determined by

1/4

ασ

⎛⎞

⎜⎟

⎝⎠

(2.62)

The heat flux through the surface

i is obtainable from the balance between the N

emitted rays and the number of absorbed rays. The dimensionless heat flux

can be written as

()

wiwi

−=

−

= 1

eff

The readers are referred to references (Siegel and Howell, 1990; Zhu, 1989; Howell,

1964a, b; Perlmutter, 1964) for the expressions of the involved cumulative probability

functions.

Monte Carlo method may result in considerable error in cases of low optical

thickness (

lmLk =

, namely the ratio between the geometrical scale and the

mean penetration distance of the photons). On the other hand, increased optical

thickness may lead to rapidly rising demands of computational capacity. Therefore

Monte Carlo method is considered efficient mostly in cases of complicated system

with sensitively changing radiation properties.

2 Modeling of the Thermophysical Processes in FKNME 

2.2.4



Discrete transfer radiation model

DTRM (discrete transfer radiation model) is a method combining the zone

partition idea from zone method and the ray tracing principle from Monte Carlo

method. This makes DTRM generally applicable to wide range of cases with

relatively lower demand to computational efforts. DTRM works especially

effective with optically thin applications.

The radiation intensity of a randomly selected ray changes as it travels through

an absorptive-diffusible medium. The governing equation is:

() () () ()( )

4π

,,,d

d4π

(I) (II) (III) (IV)

ibiii

ai x i x a i x i x

λλλλλ λ

σλ

σω

λωω ω

′

′′′ ′

=− − + +

∫

(2.63)

Term

ĉ in Eq. 2.63 denotes the absorption of the medium. Term Ċ

represents the deterioration in x direction due to scattering. Term

ċ is the

emission in x direction from the medium itself. Term

Č include all radiations in

x direction scattered by all other rays. We usually ignore the scattering term when

there are only minor particles presented in the furnace gases, which simplifying

the equation into:

() () ()

ibib

iaixaixaixa

λλ λλ λ λ

′′ ′ ′

=− + =− + (2.64)

By assuming the radiation intensity is independent of wavelength and direction,

we rewrite Eq.2.64 into:

πd

aai

+−= (2.65)

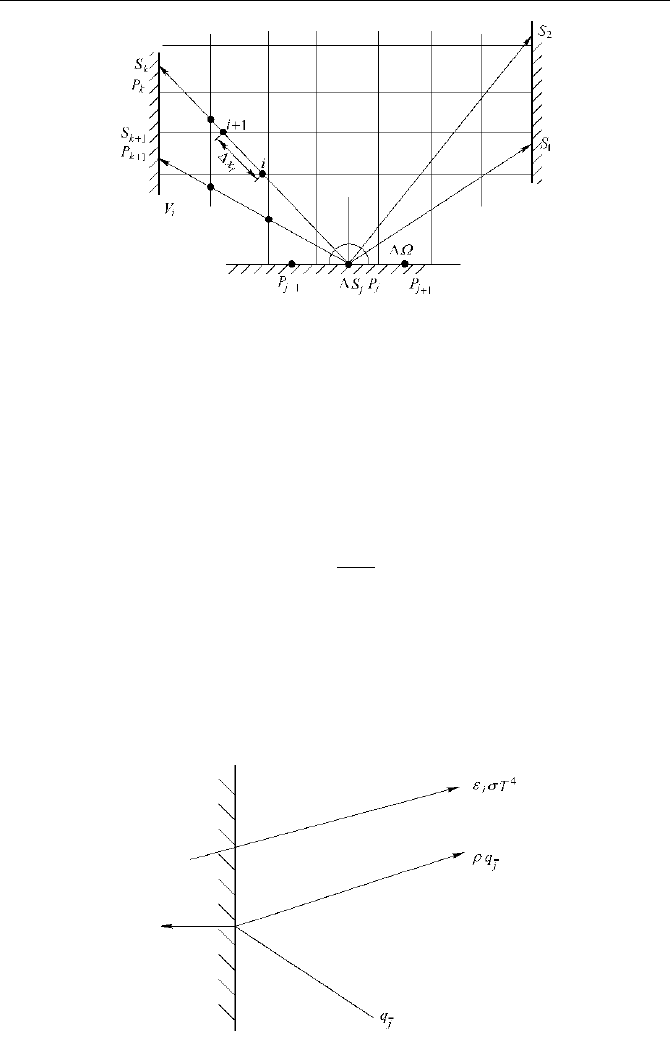
The procedure of applying DTRM is illustrated below by a 2D model.

A 2D space as shown in Fig. 2.2 is divided into i volume elements and j

surface elements. In most practices the zones are divided following the mesh

grids for computing the convection and diffusion processes of fluid flow. We

name the center point of a surface element as P

. The hemisphere around P

divided into k solid angles sections. For each of these angular sections an

emitting direction can be defined, following which a radiation ray will be

“emitted” and traced. The prediction accuracy rises if a larger number of sections

(k) is selected.

To carry out the computation, we assume as well:

a) Thermophysical properties within an element stay constant.

b) Surface elements are diffusive and gray.

c) Radiation intensity of each ray is identical.

d) All consequent effects from rays incident to surface element j are contributed

to the center point P

  Ping Zhou, Feng Mei and Hui Cai

Fig. 2.2 A schematic diagram for 2D DTRM

The implementing of DTRM becomes pretty easy once the above assumptions

having been established.

a) Going through all angular sections and tracing back each incident rays until

their emitting point. Along the tracing process, the variation of the radiation

energy is updated for each volume element the ray has traveled through. The

variation is considered as the contribution of this ray to this particular volume

element, which is described by the restructured Eq.2.65:

e(1e)

ax ax

−Δ −Δ

=+ −

(2.66)

where xΔ denotes the gain in traveling distance in this volume element; a denotes

the absorptivity of the volume concerned.

b) Once having traced back to the original emitting surface of the ray, the

radiation intensity on this surface is calculated by Eq.2.67 (Fig.2.3):

Fig. 2.3 Radiation intensity of surface element

(² is reflection coefficient; ¦ is radiation coefficient)

2 Modeling of the Thermophysical Processes in FKNME 

()

ππ

qTq

−+==

(2.67)

where

q denotes total radiation energy;

q denotes the obtained incident

energy from elsewhere;

¦ denotes the emissivity of the surface, which equals to

the absorptivity.

In case the boundary is not defined by surface temperature but by net radiation

heat flux

net

q , Eq.2.68 is used:

ππ

net

)−+==

(2.68)

The above 2D case can be easily expanded into 3D (Fig.2.4) simply by

rewriting Eq.2.67 into:

()

ωθεσε

ϕθ

dcos1

π2

π/2

∫∫

−+=

jjij

iTq

()

ωθεσε

Δ−+=

∑

cos1

jji

iT (2.69)

Eq.2.66 is still applicable for determining the radiation intensity within a

volume element.

Fig. 2.4 Solid angle θ and φ in a hemisphere

Before closing the discussion about the radiation models, we go back to the

starting point of Section 2.2.1 where the source term in the energy conservation

equation is discussed. To determine the radiation source term for each volume i,

we add up contributions from all involved parts:

()

ΔΔ

∇= =

∑

∫∫

••qqsJ (2.70)

where

()

jjjnnj

sii ΔΔ−=

cos

J is the contribution of surface element j towards

the concerned volume element i. The radiation intensities i

n+1

and i

are

  Ping Zhou, Feng Mei and Hui Cai

computable from Eq.2.66 with the starting point at i

2.3



The Simulation of Combustion and Concentration Field

Combustion is a flow phenomenon with chemical reactions producing a lot of

heat. So it also involves the characteristics of mass transfer and chemical

reactions. Apart from the characteristics of turbulent flow and heat transfer

discussed in the former sections. The interaction and strong coupling between

turbulence and combustion make the differential equations of combustion very

complicated. Generally, these equations can hardly be solved by analytical

method but numerical simulation method.

Knowing that the actual combustion processes in the FKNME applications are

mostly in turbulence, we focus in this section the simulation of turbulent

combustion, including gas phase and gas-particle two-phase combustions. The

objective of combustion simulation is to gain better understanding about the

temperatures, velocities, concentrations (species mass fraction) and heat release

(chemical reaction rate) based on the conservation of mass, momentum and energy,

and the rules governing the reaction rates as a function of temperature, pressure

and reactant concentration.

2.3.1



Basic equations of fluid dynamics including chemical reactions

For a chemical reaction system consisting of N

chemical species and probably

involving N

basic reversible reactions, the jth reaction can be written in the form

...

2211

++ XaXa

jrjr

= ...

2211

++ XaXa

jpjp

(2.71)

(i=1, …, N

) refer to chemical species. Reactants are not distinguished from

products in this equation because reactants and products are reversible in the

reactions. a

rij

and a

pij

are the stoichiometric coefficients of species i at both

sides of j th basic reaction equation. Their values are positive or zero. The

difference:

= a

pij

 a

rij

(2.72)

is the overall stoichiometric coefficient for species i in reaction j, and is positive

for products and negative for reactants.

The impacts of chemical reaction on turbulent combustion are mainly

repnesented by the source terms in transport equations. Since the momentum

equations are identical to what have been discussed in the previous sections, in

this section we mainly discuss the conservation equations of chemical species and

enthalpy and the reaction rates in connection with the source terms of these

equations.

2 Modeling of the Thermophysical Processes in FKNME 

2.3.1.1



Reaction rate

Chemical reaction rate means the species quantity produced or consumed at unit

time, unit volume (mol/(m

• s)) and is modeled as a function of reactant and

product

concentration (Fan and Wang, 1992; Fan et al., 1987), by

[] []

ij ij

jfj i bj i

Rk x k x

αω

=−

∏∏

(2.73)

or in case of reaction rates influenced by concentrations of third non-reacting third

bodies (inert species), by

[] [] []

ij ij

jijifjibji

Rxkxkx

αω

⎛⎞

⎜⎟

=−

⎜⎟

⎝⎠

∑

∏∏

(2.74)

where [x

] is molar concentration of species i;

is forward rate exponent;

backward rate exponent;

is efficiency of species i as a third body (0İ

1);

is forward rate constant; k

is backward rate constant.

Rate constant can be calculated as a function of temperature from the modified

Arrhenius law. For the j th forward reaction, this is

fj fj fj fj

ERT TT

fj fj fj

kAT AT

ββ

−−

(2.75)

where A

is pre-exponential factor or frequency factor;

is temperature

exponent; E

is the activation energy; T

is the activation temperature (or E

/R).

The backward rate constant can be defined similarly.

2.3.1.2



Species conservation and mass continuity equation

General mass fraction Y

(i=1, …, N

) represents chemical species concentration,

then mass conservation equation for species can be written as (Fan et al, 1987)

()

ii i

∂

+∇ + =

∂

• UJ (2.76)

where

U=˄u, v, w˅ is average velocity of the mixture (u, v, w stand for velocity

components in three orthogonal coordinate directions, respectively );

is the

density of the mixture; t is time; J

is the mass flux of species i relative to the

mean (bulk) flow, kg/(m

• s); S

is the product and consume rate of species i due to

chemical reaction. Here

()

iii

≡−JUU (2.77)

where

is the velocity of species i. The first, second, third term on the left hard side

and the term on the right hard side in Eq. 2.76 are called respectively the time

variation rate term, convection term, diffusion term and reaction source term of

species i.

According to Fick’s law

(2.78)

40 Ping Zhou, Feng Mei and Hui Cai

==-[rj+~:)v~

where IlT is the turbulent viscosity,

is turbulent Prandtl numbers. The mass

conservation equation

species i is defined by

a~;

+ V

.{PU~

r,+

)v~

}

S, (2.79)

the species source term due to chemical reaction (kg/nrr' • s)) is summed from the

contributions

the reaction rates by

MiLnijR

j=l

where M is the molecule weight for species i, R

is the j th reaction rate.

2.3.1.3 Enthalpy equation

(2.80)

(2.81)

Enthalpy equation is the application

the first law

thermodynamics to fluid

dynamics and can be expressed as that the increase

total energy per volume is

equal to the sum

the net incoming stagnation enthalpy, the heat transfer and the

work from the surroundings. How to choose the variables in the energy equation has

a great influence on the equation solving process. For the combustion system with

multi-species and chemical reactions, the four kinds

mixture enthalpy are usually

used as dependent variable in energy equation: thermal enthalpy, thermal enthalpy

chemical enthalpy, total enthalpy (thermal enthalpy + chemical enthalpy + kinetic

energy) and sensible enthalpy (thermal enthalpy + kinetic energy).

the work from external bulk force and other external heat sources apart from

thermal radiation are neglected, the equation for total enthalpy is (Zhou, 1994;

Carol, 1987)

[p(

-~)]+

V•

(pUH,

)

cIJ+Qrad

-V

-s,

where (/J is viscous dissipation, or shear deformation work;

Qrad

is source term

(radiative heat); qt is total energy flux (including the energy carried into by

thermal conduction and species diffusion):

=-AVT+

LJiH

A is thermal conductivity; H; is total enthalpy

species i and can be written by

tt,

hfi

~ (~U2

+k) (2.82)

hfi is specific enthalpy

formation

species i, U is the averaged velocity

the

mixture, and

k is the turbulent kinetic energy.

The energy equation with sensible enthalpy (H) is more generally applied in the