Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

2 Modeling of the Thermophysical Processes in FKNME 

2.1.4



Low Reynolds number k-

models

The low Reynolds number flows are not rare in FKNME applications, such as the

recirculation zone of a sudden expansion flow at the outlet of the nozzle; the

close-to- wall boundary flows, viscous molten mass and viscous molten slag flows

etc. These cases should be better modeled by the so-called Low Reynolds Number

(LRN)

models.

W.P.Jones and B.E. Launder (Jones and Launder, 1972) proposed the first

correction to the standard

model for low Reynolds number flows, in which the

following phenomena have been considered:

a) The viscous diffusion of

k and

b) The changes of the turbulent viscosity and turbulent energy dissipation as

functions of Reynolds number, the turbulent viscosity should decrease as the

Reynolds number falls.

c) The sensitivity of

towards the direction in the area close to walls.

Jones and Launder inversely deduced the correction functions for

μ , k and

based on experimental observations, which led to the first LRN k-

model:

μμ

= (2.32)

+−+

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

ρε

μρ

)( (2.33)

εεε

ρε

εε

μερ

EfCGfC

kxx

+)−+

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

2 211

(( (2.34)

where

2/1

⎟

⎠

⎞

⎜

⎝

⎛

∂

−=

⎟

⎠

⎞

⎜

⎝

⎛

∂

μμ

n is the distance normal to wall.

0.1

()

exp3.00.1

Ref −−=

με

Boundary conditions:

= 0 on walls.

  Ping Zhou, Feng Mei and Hui Cai

where f

, f

are the damping functions. The LRN k-

model can be

numerically solved in the way same to solving the standard

model, except

that no more wall functions are necessary for determining the variables on the

walls. Instead, one needs to arrange 20 to 30 mesh points along the direction

vertical to the wall. That is why sometimes LRN models are called as “direct

approach for wall boundaries”. However, the large demand of computation in the

vicinity of the walls brings a lot of difficulty to numerical convergence, which

accounts for the imposing of

=0 on the boundaries to simplify computation.

The

term in the turbulent energy equation is particularly introduced to balance

the dissipation term on the wall, which actually does not equal to zero.

A lot of other LRN

models have been developed following the ideas of

Jones and Launder. A number of the most frequently used LRN models have been

listed in Table 2.5.

The LRN

models have been extensively investigated and developed in 1970s and

1980s and have been increasingly applied to engineering practices. The LRN models

are very useful to predict low Reynolds number turbulent flows and other flows where

the wall functions are difficult to apply, e.g., flows through or over a narrow gap and

flows with dominating body forces or substantially changing fluid properties.

The disadvantages of the LRN models are also obvious. The damping functions

are deduced from laboratory measurements, which are not generally applicable.

Different corrections have been reported by a large number of researchers based

on their own studies and interpretations to the problems. This leads to the

emerging of a large variety of LRN models with relatively limited range of

applicability. It is highly recommended to be clearly aware about the range of

validity of a LRN model before using it for one’s own simulation. Experimental

validation is sometimes quite necessary if no report can be found about the

performance of the concerned LRN model for the specific application. The second

weak point of LRN models is the requested computational capacity that is much

larger than that of the wall function approach. This explains why the LRN models

become popular only when the high-speed computers have been widely available.

One more important issue that has been frequently overlooked is that the LRN

models do not guarantee good performance on temperature field prediction, because

they are developed based on flow field measurements. For example, in simulating the

sudden expansion flow and heat transfer, the Nagano-Hishida model predicts a peak

Nusselt number 100% higher than the measurements. Further more, this model

predicts a second Nusselt number peak that physically does not exist. This peak

persists after applying the correction proposed by C. Yap (Yap, 1987; Ramamurthy, et

al., 1993). Who tried to improve the performance of the Nagano-Hishida model. Same

problem exists with the Jones-Launder model and the Launder-sherma model in

computing the same sudden expansion flow. The peak Nusselt numbers predicted by

these two models have been found four times as high as the measurements.

2 Modeling of the Thermophysical Processes in FKNME 

  Ping Zhou, Feng Mei and Hui Cai

2 Modeling of the Thermophysical Processes in FKNME 

2.1.5



Re-Normalization Group (RNG) k-

models

The afore-mentioned k-

models are established based on the theory that the turbulent

fluctuation can be considered as an extra viscous effect added on top of the molecular

viscosity. This extra viscous effect is found proportional to

ρk

and the coefficient

can be determined via experimental data. This is a typical hybrid modeling

approach that combines theory, compromising assumptions and empirical observations.

Surprisingly, a very similar result can be obtained from a pure mathematic derivation

starting from basic turbulent theories. This is the Re-Normalization Group (RNG)

model developed by V. Yakhot and S.A.Orszag in 1986 (Smith and Reynolds, 1992;

Lam, 1992; Yakhot and Orszag, 1998; Yakhot and Smith, 1992) with isotropic

assumption to high frequency turbulence (small scale eddies). Yakhot and Orszag

studied the turbulence phenomena using frequency spectrum analysis and reorganized

the N-V equations in wave vector form. From this new perspective, the large eddies

are equivalent to low frequency, long wave length oscillations and the small eddies are

high frequency and short wave length oscillations. The low frequency sectors are the

major energy holders whereas the high frequency sectors are of no importance in terms

of energy contribution to the system. The approach of Yakhot and Orszag was to

“cut-off” first an infinitesimal part of the spectrum from the high frequency end and

then add back the equivalent effect of this lost part to the system by appropriately

estimating the impact of the cut section in the spectrum. From the viewpoint of

turbulent, this impact is reflected by the change of the viscosity. By repeating this

process the high frequency waves have been gradually filtered out but the contribution

of these sections to the turbulent effect has been preserved. In the early days of this

model, the spectrum was renormalized each time after the cut off process. That is why

the model is called the “Re-Normalization Group” model or RNG model. The more

recent RNG model can be done through a so-called

-expansion, in which

does not

stands for the turbulent energy dissipation but an assumed source of high frequency

noise. After this renormalization process, the N-S equations set is transformed into the

following RNG

model, which is pretty similar to the standard k-

model (Yakhot

and Orszag, 1992):

+−

∂

εμα

(2.35)

xxx

+−+

∂

εε

εμαε

εε

(2.36)

ερμ

′

(2.37)

)/1(

βη

ηηηρ

−

(2.38)

  Ping Zhou, Feng Mei and Hui Cai

where

/Sk=

()

2/1

⎟

⎠

⎞

⎜

⎝

⎛

== GSSS

ijij

015.0

38.4

68.1,42.1,39.1,0837.0

====

′

εεμ

CCC

Comparing to the standard

model, the major difference is an extra R term in

the dissipation equation. It can be considered as the contribution from the strain

rate of the flow. It has been indeed found in the laboratory research that the

R term

becomes significant at locations with large strain rate and substantial anisotropic

effect, such as in the vicinity of the walls (Shea and Fletcher,1994). On the other

hand, the

R term decays remarkably at locations where the strain rate is small or

the flow turns to be isotropic, which transforms the RNG model into a high

Reynolds number

model. From this point of view, the R term is pretty similar

to the damping functions in the LRN models. Different from most other terms in

the model that are through mathematic derivation, the determination of the

R term

was partially through physical and mathematical analogies. Even though the

term is not universally applicable, it is still true that the

R term is much more

widely applicable than most of the damping functions in the LRN models.

The value of

′

applied in the RNG model is slightly lower than the

empirically determined

′

=0.09 which is used by the standard Reynolds number

model. Note that we often take

′

= 0.085 instead of 0.0837 in practice.

There are actually more than one RNG models. The turbulent Prandtl numbers in

the

k and

equations can be expressed as functions of μ

. And μ

itself can also be

modeled in differential or algebraic expression. These modifications can improve

the performance of the model under low Reynolds number flows but also add

extra difficulties to the numerical process. The RNG model introduced in this

section is a very basic version. The readers are referred to Chapter 9 for further

discussion on the applications of RNG

model.

2.1.6



Reynolds stresses model(RSM)

The turbulent models discussed in the previous sections are all based on the

turbulent viscosity assumption. The advantage of these models is the simplicity of

modeling whereas the disadvantage is the isotropic presumption that may not

apply to anisotropic turbulence such as the nature convection, swirling and

near-wall flows. The RSM tends to model the Reynolds stresses individually in

each direction so that anisotropic processes are allowed. The weakness of RSM is

the high demand to computation capacity. For a 3D problem with heat transfer

2 Modeling of the Thermophysical Processes in FKNME 

process, a RSM may require solving 11 differential equations. Besides, the

physical foundation of the modeling of the pressure-strain term is not sufficiently

sound. Therefore the RSM actually does not necessarily predict more accurately

than the standard

model in cases of considerable variation of density. Too

many constants involved is sometimes also a problem for applying RSM when

there is no sound experimental data to validate these constants in a particular case.

For these reasons RSM is not often the appropriate option in FKNME applications

unless the users have developed sufficient experience in using RSM. Nevertheless,

RSM should still be considered very promising in engineering applications in the

future when noticing that both CFD techniques and computational capacity have

been sufficiently developed.

2.2



The Modeling of the Heat Transfer in FKNME

Heat transfer in the FKNME involves processes of conduction, convection and

radiation; however, it is dominated by radiation and combustion in most cases. In

this section, we will focus to introduce methods of radiation computations.

2.2.1



Characteristics of heat transfer inside furnaces

The heating processes in the FKNME are mostly realized through the ways as

listed in Table 2.6.

Table 2.6 Heat transfer in the FKNME

No.

Heating

mechanism

Physical models Mathematical models Examples

Solids heated by

electric current

Coupling of electrical

and thermal

conductions

Laplace’s equation for

electrical conduction

Poisson equation for

thermal conduction

Temperatures

computation in

carbon electrode

By electrical heat

source in molten

mass

Coupling of

electroma

netic flow

and turbulent heat

transfer

Electromagnetic Field

equations

Navier-Stokes

equations

In bath of indu-

ctance furnaces

and aluminium

reduction cell

By chemical

reaction heat

released in molten

mass

Coupling of turbulent

flow and gas-solid

chemical reactions

Navier-Stokes

equations

Chemical reaction rate

equations

Converter

process

By hot gases

(towards solid

objects)

Coupling of convection

(on surface) and

conduction (within

the solid body)

General turbulent mot-

ion equations

Poisson equation for

thermal conduction

Convective heat trans-

fer empirical equations

Heating furnace

with hot air

recirculation

  Ping Zhou, Feng Mei and Hui Cai

Continues Table 2.6

No.

Heating

mechanism

Physical models Mathematical models Examples

By flames in

direct contact

(towards solid or

molten mass)

Coupling of

turbulent flow,

combustion and

heat and mass

transfer

Single-fluid or

two-fluid model

General turbulent

motion equations

Radiation model

Chemical reaction

models

Smelting or heating

Furnaces boiler-

furnaces

By flames in

separated

chambers

Coupling of heat

transfer processes

a) Flames to wall

b) Within the wall

c) Wall to load

Single-fluid or

two-fluid model

General turbulent

motion equations

Radiation model

Chemical reaction

models

Thermal conduction

equation

Retort furnaces

Carboneletrode

baking furnace

In the fluidized

bed system

Gases-particles

heat transfer

Fluidized beds to

the closure wall

and the immersed

objects’ surface

Empirical equations

Sulphide concent-

rate roasting furnace

Dilute-phase-type

fludidigation

furnace

By surface

radiation

Coupling of

radiations between

enclosed surfaces

Zone method

Monte Carlo method

or radiation network

method

High temperature

electric-resistance

furnaces

Radiation rube

As shown in the Table 2.6, the heat transfer processes in the FKNME are

remarkably complex. If we may still state that we know something about

turbulence, we would probably have to admit that we do not have much clear idea

about heat transfers in the fluid flows. This partially results from the extreme

difficulty to measure temperatures in the flows with high accuracy. Most of our

analysis work to the heat transfer processes in flows is actually via analogizing to

velocity fields, which means we presume (with some reasons) enthalpy field is

similar to the flow field. This assumption allous us to write the enthalply transport

equation in the following way under the

k-ε model:

()

Prx

⎥

⎦

⎤

⎢

⎣

⎡

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

where

h denotes the enthalpy in the flow which is defined as:

∑

∫∫

∑

⎥

⎦

⎤

⎢

⎣

⎡

++==

apa

TcYhYh

ref

dd (2.39)

where a is chemical species

ˈa˙1ˈ2ˈ…ˈn˗

Y is mass fraction of a;

2 Modeling of the Thermophysical Processes in FKNME 

specific heat at constant pressure of a;

h is enthalpy of formation of a;

ref

T is

referential temperature to

h ;

T is standard temperature,

T ˙273K (0ć);

M is molecular mass of a.

ěY

stays constant that should equal to 1 in case of no chemical reaction,

which turns the enthalpy definition equation into a simplified version:

∫

Tch

ref

This definition is further simplified by assuming c

is independent of

temperature:

Tch

The above enthalpy transport equation and the general turbulent equation can be

used to solve the heat transfer field in most flows prevailed by turbulence such as

molten mass flow with internal heating source or solid objects heated by hot air.

To general fluidization system, however, empirical equations are still more

frequently used for computing heat transfer (the readers are referred to Chapter 8

for details). In the high temperature flames furnaces, especially those fired by

pulverized coal or heavy oil that are of high emissivity and absorptivity, the heat

transfers are dominated by radiations and (or) combustion. In these cases, the

major efforts should be put on properly handling the computation of radiation and

chemical reactions, which are represented by the source terms in the enthalpy

transport equation.

Radiation can be computed by algebraic equation in the simplest cases such as

radiations among surfaces in enclosure with approximately uniform temperature

distribution on each surface. The zone method or the radiation network method

(electric resistance analogy method) can be applied if uniform surface temperature

cannot be assumed. If situation gets more complicated, such as in cases of

non-uniform temperature field in gray medium, we may consider heat flux method,

zone method, Mont Carlo method or discrete transfer method.

2.2.2



Zone method

Zone method has been proved efficient for computing enclosures with simple

geometry and minor temperature variation. The basic idea of zone method is to

divide the enclosure into a number of surfaces and areas (or volume in 3D)

elements. The physical properties are assumed staying constant within each

element; the medium is assumed gray and the surfaces are assumed of

diffusive and gray (Robert and John,1990;Mei et al., 1997; Wang, 1982; Zhu,

1989).

Fig.2.1 illustrates the radiation between the volume V

and the surface A

. The

finite radiation heat flux from the volume dV

within the wave length bandwidth

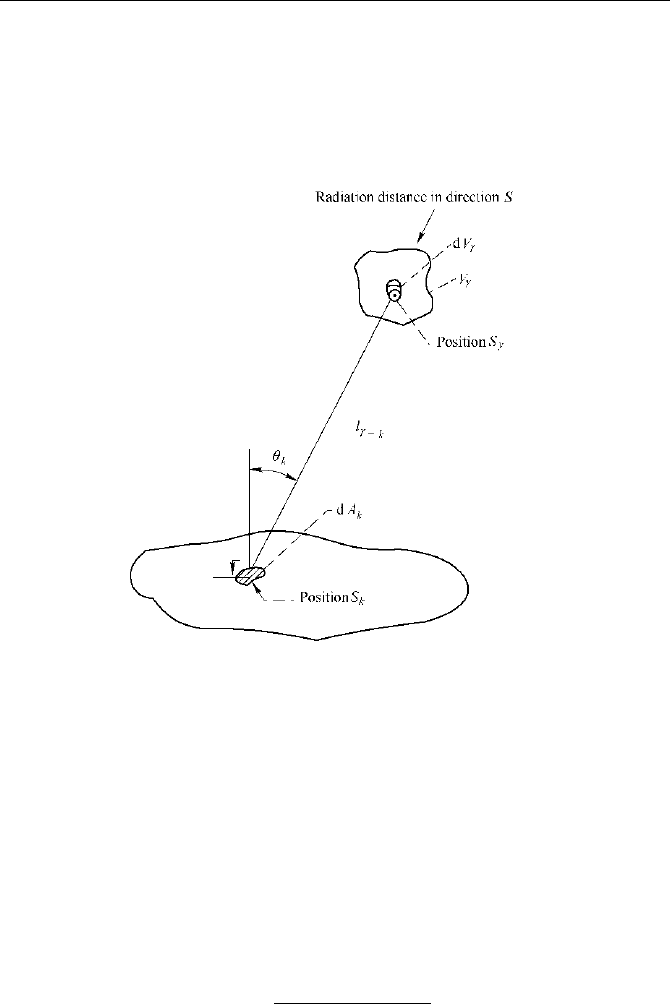
  Ping Zhou, Feng Mei and Hui Cai

dλ is written as:

wVIQ

dddd

π4

λε

γλλλ

∫

γλλγλλ

dd4ddπ4 VEVI

(2.40)

Fig. 2.1 The radiation between surfaces and gray gases

where

is the monochromatic emissivity of the gas,

is the monochromatic

energy density of black body in unit W/(m

• ) (Wang, 1982) ; the radiation heat

flux from

Vd in the solid angle within wave length range d

equals to

γλλ

ddVI

. The transitivity

()

lPT ,,,

of the heat flux through the distance

−

is:

()()

lPTlPT ,,,1,,,

λλ

−=

)exp( l

−= (2.41)

where

is the monochromatic absorptivity of the gas. Integrating over volume

V and surface A

results in the monochromatic radiation heat flux:

() ()cos

dd dd

lk l k

HA A V

λλ

εγ γ θ

λτ

−

∫∫

•

•• •

(2.42)

Further integrating Eq.2.42 over wave length leads to the total incident heat flux

to the surface A