Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

where

is the equivalent diameter of the bubbles;

is the volume fraction of

the bubbles in the dense phase.

Although this model has made one step closer to the reality by adding the

independent bubble cloud phase, the major weakness of this model is obvious,

because neither the changes of the bubbles nor the impacts of these changes along

the bed height have been taken into account.

8.4.3



Bubble assemblage model (BAM)

The bubble assemblage model has considered the growth of the bubbles in the

fluidized bed. Therefore it is even closer to the practical situations compared to the

previous two models.

The basic assumptions of BAM are as follows(G.S.,1993):

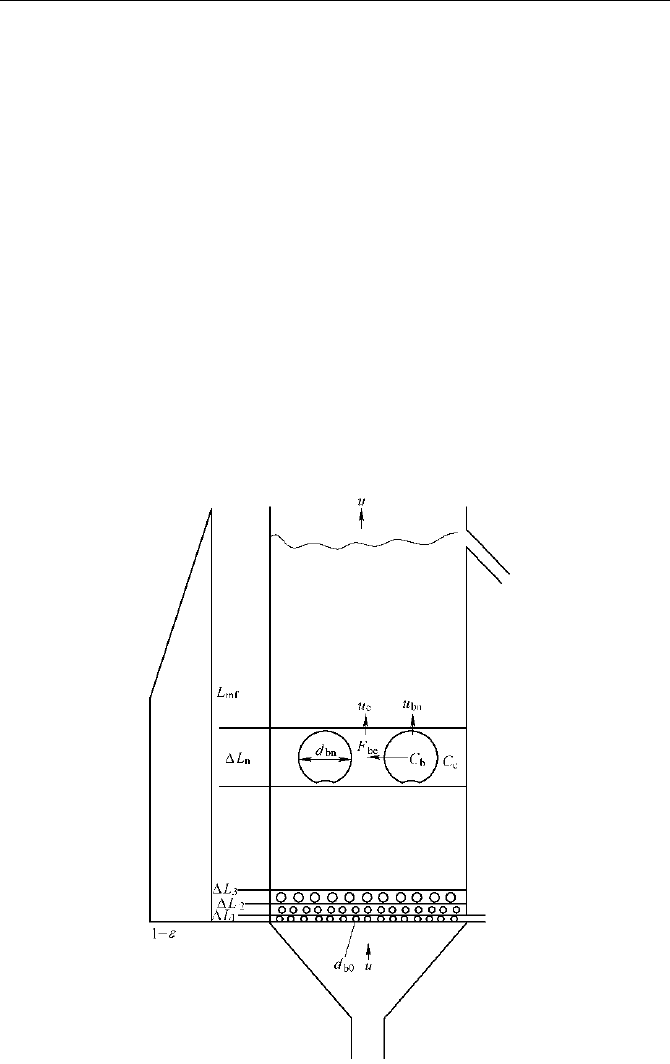
a) From the distribution board upward, the fluidized bed layer is divided into

several consecutive sublayers. The height of each sublayer equals the size of the

local bubbles (Fig. 8.9).

Fig. 8.9 Schematic of parameters in the bubble assemblage model(BAM)

  Chi Mei and Shaoduan Ou

b) Each sublayer contains bubble phase and emulsion phase, and the gas is well

mixed in each phase.

c) The void volume in the emulsion phase equals the value when the bed layer

starts fluidization, namely

mfe

≈

. Meanwhile, it is assumed that the velocity of

the gas in the void of the emulsion phase is so low that it can be neglected (namely

when

11~6/

mff

≈uu

≈u

d) The bubble phase is composed of spherical bubbles and their surrounding

spherical clouds.

e) The total volume of the bubbles in the bed layer is

()

fmf

LLA−

, where

the cross section area of bed layer.

f) The gas exchange coefficient between the bubbles and the emulsion phase is

related to the bubble size:

11/Fd=

(8.75)

g) The voidage (

¦) measured from the bottom to the height

of the bed is

a constant, and then increases linearly with the height. Assuming this value

reaches 1 at the height of

()

mf mf

2LLL+−

, that is to say,

at Z

()

mf mf

−

−=

(8.76)

İZİ

()

LzLL+−

()()( )

()

mf mf mf mf mf

LLLL

LLL

εε

−−−

−= −

−

(8.77)

The BAM can be solved by making material balance within each sublayer. For

the bubble phase in the

th layer, the material balance is

() () ( ) ( )

bb bebbebe

nn n

uC C FV C C rV•

−

⎡⎤

−= −+

⎡⎤

⎣⎦

(8.78)

where

is the gas exchange coefficient per unit bubble volume.

(8.79)

br mf mf

Total volume of bubble phase (void cloud)

Volume of bubble void

Diameter of cloud

Diameter of bubble

⎛⎞

⎜⎟

−

⎝⎠

(8.80)

where,

()

0.5

0.711

ugL

=Δ (8.81)

In Eq. 8.78,

r is the volumetric reaction rate of the solid material (with voidage

) in the cloud phase. Under the first order reaction condition,

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

rkC= (8.82)

where k is a constant;

V and

V represent the total bubble volume (void +

cloud) and the cloud volume in the sublayers, respectively. The total volume of the

bubble phase is:

()

bbv

void cloud

NLr

VVr

•

+= =

(8.83)

The volume of the cloud phase is:

()()

π 1

NLr

Δ−

= (8.84)

Material balance of the emulsion phase (for the

th layer) is:

[

]

()

be b b e b e

'( )

VCC rV×− = (8.85)

where, under first order reaction condition of the gas phase,

kCr = (8.86)

V is the volume of the emulsion phase on the

th layer:

VLAV

−Δ= (8.87)

The assumptions from a) to g) mainly apply to the gas phase reactions in the

fluidized beds of catalysts particles. Modifications and corrections have been

reported as follows:

a) Kefa Cen et al. proposed an empirical bubble size correlation applicable to

wide-range bed material(Cen et al.,1997 ):

0.576

0.346

0.711

bm 0

0mf g

30.576

−

⎛⎞

−

⎜⎟

⎝⎠

(8.88)

where

H is the static height of the bed, m; L is the distance to the bottom plate, m.

b) Maximal bubble size(Movi and Wen,1976):

()

0.4

bm mf

0.652dAuu=−⎡⎤

⎣⎦

(8.89)

c) Height of the sublayer:

()

bbm

10.15 ' /

ddD

Δ=

(8.90)

where

' is the

d at the interface between the

()

1−n th sublayer and the nth

sublayer. D is the equivalent diameter of the bed.

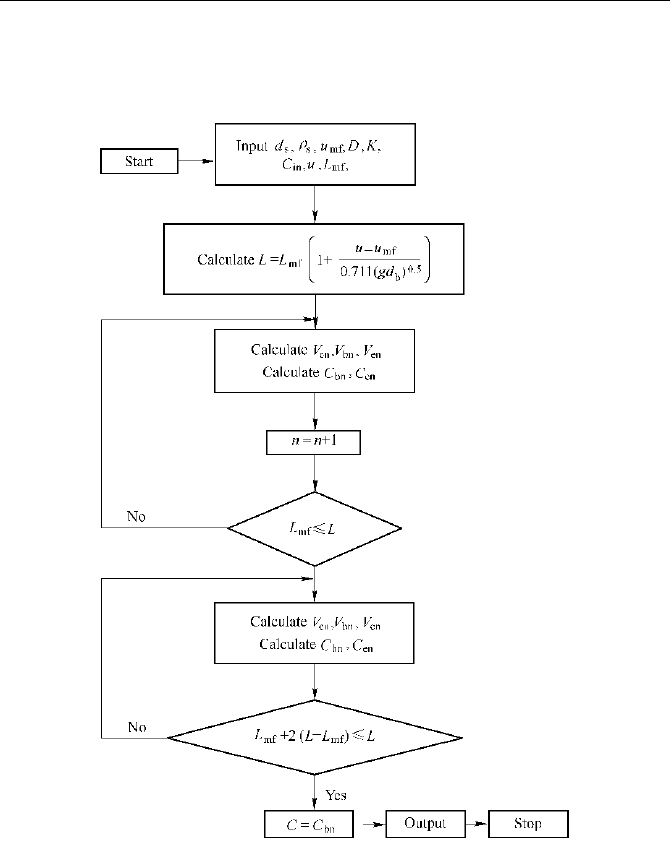
The computation procedure of BAM is as follows:

a) Calculating the jet height

L from the distributing plate. The correlation

proposed by Kono (the editorial committee of

Ā Chemical Engineering

Handbook

ā,1989) is recommended:

0.187

0.2

or s s mf

7.5

dgdu

•

⎛⎞

⎜⎟

⎝⎠

(8.91)

b) Calculating the bubble size

d at the height of

using Eq. 8.88.

  Chi Mei and Shaoduan Ou

c) Determining the height of the n th sublayer with Eq. 8.90.

d) Determining the height

+= (8.92)

where

∑

−

Δ=

LL , which is the distance from the bottom plate to the n th

sublayer. The bubble size (

d ) at this sublayer can be determined by

L .

e) Determining the height of the last sublayer:

LLL '

−=Δ (8.93)

f) The bubble fraction

at the n th sublayer can be determined by the

following equation:

−

= (8.94)

() ()

0.5

bmf b

0.711uuu gd=− +

The bubble volume in the

n th sublayer is

LAΔ

g) The total volume of the bubble and bubbles cloud

in the n th sublayer:

()

nnnn

LAV

cbb

+Δ= (8.95)

where

()

mf mf

br mf mf

0.5

volume of bubble cloud

volume of bubble /

0.711

Vuu

ugd

===

−

(8.96)

h) Determining the height of the first layer, which is usually set at the distance

from zero to

jbo

Ld+ . The bubble size at

L = is used to determine

LΔ ;

The initial bubble size

d can be estimated by the following equation (Darton et

al.,1977):

()

4.0

5.0

mfbo

/63.1

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−= g

uud (cm) (8.97)

where

()

nA/ is the average cross section area of the holes in the distribution plate,

i) Determining the total volume of the emulsion phase in the

n th sublayer:

nnn

VLAV

−Δ= (8.98)

j) Determining the interphase exchange coefficient

'k based on the total

volume of the bubbles and bubble clouds:

⎟

⎠

⎞

⎜

⎝

⎛

−

mfjfbr

mfmfbr

kk (8.99)

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

Using the material balance equations( Eq. 8.78 and Eq. 8.85), the sublayers can be

computed from bottom to top following the above steps. The flow chart is shown

in Fig. 8.10.

Fig. 8.10 Computation scheme for the BAM of gas-phase reactions

8.4.4



Bubble assemblage model for gas-solid reactions

The BAM discussed in the previous section is developed for gas-phase estimation

but this model is also applicable to the gas-solid reactions after making some extra

assumptions in addition to those mentioned in section 8.4.4.

a) Defining J

as the ratio of the particle volume in the cloud phase to that in the

bubble wake,

  Chi Mei and Shaoduan Ou

()

smf

volume of particles in bubble cloud and wake

volume of bubble

γε

⎛⎞

−

=−

⎜⎟

⎝⎠

(8.100)

where

is the share of the particles in the bubble phase.

bω

−

≈

where

is the ratio of the volume of the bubble wake to that of the bubble.

Generally, we have 5.0~12.0

≈

for industrial fluidized beds. This value

declines as Ar rises (Rowe and Partridge,1965 ).

In Eq. 8.100,

is the share taken by the bubbles in bed layer. For most

engineering applications, we have

−

≈ (8.101)

In the emulsion phase, we define



as the ratio of the volume of the particles to

that of the bubbles:

()

mfe

1 JJ

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

(8.102)

b) The particles that have been dragged up by the bubbles and bubble wakes are

compensated by those brought down in the emulsion phase. The overall flowing

direction of the particles is dependent on whether it is forward feeding (bottom

feeding) or backward feeding (top feeding). For the

n th sublayer, the total flow

rate of particles moving upward is:

ωs

⎟

⎠

⎞

⎜

⎝

⎛

δω

(8.103)

where

is the cross section area of the bubbles in the n th sublayer:

()

3 −

= (8.104)

is the volumetric feeding rate (being positive for forward feeding and negative

for backward feeding). The total volumetric flow rate

()

1e +n

of the particles

flowing into the next sublayer is:

()

AAA

−

⎟

⎠

⎞

⎜

⎝

⎛

−

ωδ

(8.105)

c) Particles exchange between the bubble phase and the emulsion phase with the

exchanging coefficient estimated by the following correlation equation:

()

mf mf b

mf br b

•−

≈ (s

−1

) (8.106)

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

where

()

is the particle exchange coefficient, s

-1

. An isolated bubble rises in

velocity

()

5.0

bbr

711.0 gdu = whereas in the bubbling bed the bubbles rise in

velocity

mfbrb

uuuu −+= .

A simplified approach in engineering applications is to assume infinitively large

particles exchanging coefficients in each sublayer, that is to say, the particles in

each sublayer are perfectly mixed.

As discussed in the previous section, similar material balance relations as

expressed in Eq. 8.78 and Eq. 8.85 have to be applied in each sublayer.

For the bubble phase:

() () ( )

[

]

b b be bv b e e bv r b

uC C FV C C jVKC

−

⎡⎤

−=×−+

⎡⎤

⎣⎦

(8.107)

where

F (see Eq. 8.75) and

j (see Eq. 8.91) are based on the bubble void

volume

V ;

V is calculated by Eq. 8.83.

Regarding the emulsion phase, we have:

()

[

]

be b v b e e bv r e

VCC jVKC−=

⎡⎤

⎣⎦

(8.108)

Given that particles are perfectly mixed, the effective gas concentration

experienced by the particles can be calculated by the following equation:

()()

eebc

CjCj

= (8.109)

With all these parameters well determined, the time t* for a complete particles

conversion can be calculated (refer to Section 8.4.6).

Under the ash diffusion control condition, we have:

bD C

•

= (8.110)

where

d is the average particle diameter;

is the mole density of particle

reactant; b is the mole number of solid reactant per unit mole gas; D is the mass

diffusivity of gas in the ash layer, cm

/s.

The mean residence time of particles in the

n th sublayer is given by:

()

vc e

Vjj

(8.111)

The particle conversion rate of each sublayer in the dense phase can be calculated

using Eq. 8.109 to Eq. 8.111 together with the conversion rate equations that will

be introduced in the next Section 8.4.6.

8.4.5



Solid reaction rate model in dense phase

There are two major factors determining the reactions of the solid in the dense

phase, namely the chemical reaction dynamics and the particles residence time in

  Chi Mei and Shaoduan Ou

the reaction zone.

The analysis of the dynamics of gas-particle reaction is based on the

understanding of the conversion rate of a single particle. There are two reaction

models, which are the homogeneous reaction model applicable to porous particles

(reactions take place throughout the particle) and the shrinking core model

applicable to nonporous particles (reaction takes places on the shrinking surface of

the unreacted core).

8.4.5.1



Simple homogeneous reaction model

Basic assumptions:

a) Gaseous reactants penetrate through the whole particle.

b) The particle is isothermal and homogeneous.

Under the condition of the first order reaction that depends on the gas

concentration, the reaction rate of the solid is

vAS

kCC

=−

•• (8.112)

The solid reaction rate is defined as

SO S

−

= (8.113)

()

SSO B

1CC X=− (8.114)

Therefore

()

ev A B

•=− (8.115)

where

C ,

C and

C are respectively the mole concentration of the gaseous,

solid reactant species and initial solid reactant species;

k is the reaction rate

constant of unit solid volume. Assume

C and

k are constants, then

()

BvA

1exp

kCt=− − (8.116)

∞→

as 1

→X .

We define

999.0

t as the time needed to complete 99.9% of the reaction for the

homogeneous reaction model:

0.999

ev A

6.908

•

= (8.117)

This model maybe used to estimate approximately the processes such as gasification

and burning of porous carbon and the reduction and chlorination-evaporation of the

pellets, etc. The readers are referred to literatures (Sohn and Wad- sworth, 1979; Xiao

and Xie, 1997) for more accurate models.

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

8.4.5.2



Shrinking core model for nonporous particles

Reactions of this kind can be generally expressed as:

()( )()( )

A gas phase B solid phase P gas phase R solid phasebpr+=+ (8.118)

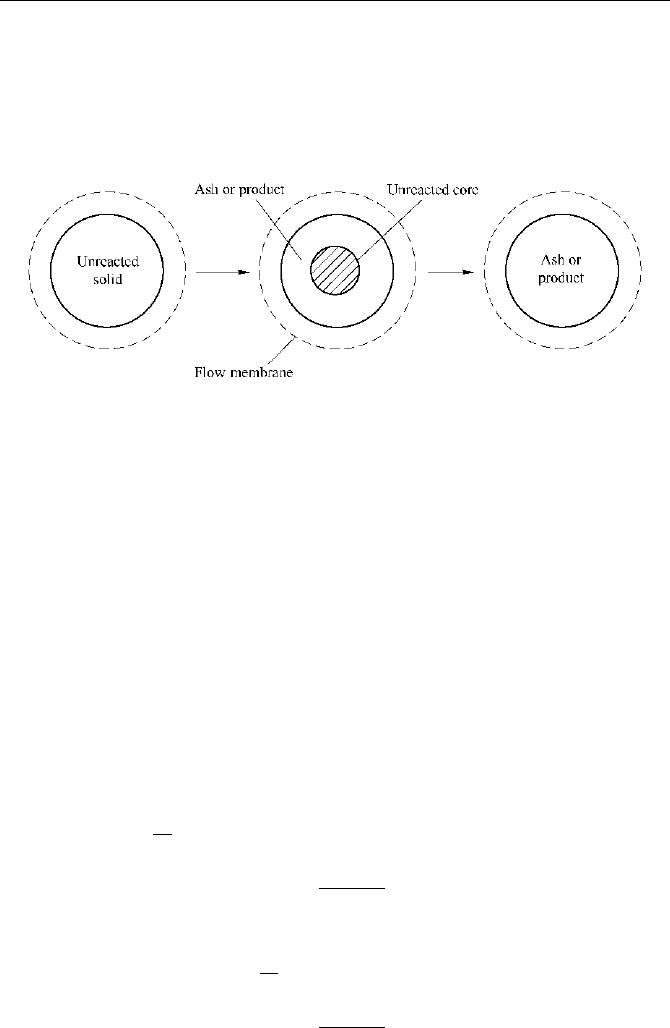
The reaction process of a single spherical nonporous particle is shown in Fig. 8.11.

Fig. 8.11



Reaction process of the shrinking core model

This model assumes:

a) Reaction only initializes on the surface of the particle, which results in a

layer of solid product (also called ash layer).

b) Gaseous reactant diffuses through the ash layer into the unreacted core where

reaction goes on; the thickness of the ash layer equals the thickness of the reacted

layer (the solid particle size keeps unchanged).

c) Gaseous product diffuses outwards through the ash layer with mass

diffusivity and mass fluxes equal to that of the gaseous reactant.

d) The instantaneous rate of mass transfer between gas and particle surface,

gaseous reactant diffusion through ash layer and gaseous product diffusion

outward are equal (quasi-steady-state).

Levenspiel(Levenspiel,1962) and Wen(Wen,1968) reported their work on the

solution of this model, which is summarized as follows:

Outwards gas diffusion control condition:

= (Equivalent to zero order reaction) (8.119)

sms

6 Cbk

= (8.120)

Chemical reaction control conditions:

()

3/1

11 X

−−= (8.121)

sms

2 Cbk

= (8.122)

Ash diffusion control conditions:

  Chi Mei and Shaoduan Ou

()()

3/2

12131 XX

−+−−= (8.123)

Afa

24 Cb

= (8.124)

In the above equations,

is the gas diffusivity in the ash layer, cm

/s;

k is

the mass transfer coefficient between gas and the surface of particles, cm/s;

k is

the rate constant of chemical reaction based on the particle volume, cm

/(mol⋅s);

is the mole density of solid reactant, mol/cm

When the chemical reaction rate is at the same order of magnitude of ash

diffusion,

k can be used to replace

k in Eq. 8.122, and k is

−

⎟

⎠

⎞

⎜

⎝

⎛

k (8.125)

If there is no more solid product around the shrinking core (for example, the

product is gaseous or the ashes have fallen), the equation of chemical reaction

control condition (Eq.8.122) can be used. If the diffusion resistance through the

surrounding gas membrane is comparable to that of the chemical reaction

resistance, the following equation can be used:

−

⎟

⎠

⎞

⎜

⎝

⎛

k (8.126)

The shrinking core model can be used to estimate the oxidations of metal

particles, the oxidations or sulfating roasting of sulfide concentrate powders. It can

also be used to assess gaseous reduction of oxide powder and burning of

ash-containing coal, etc. In practice it is unrealistic for the solid particles to

remain spherical or keep the total volume of particles unchanged. Readers may

refer to reference(Sohn and Wadsworth,1979;Xiao and Xie,1997) for corrections

in case that the real conditions are considerably different from the assumptions of

this model.

8.4.5.3



Average reaction rate (

) of the particle groups in the dense phase

The previous sections have covered the estimations of conversion reaction rates

and reaction times, and the average reaction rate can be obtained if the dense

phase particles distribution function at the outlet is available

()()

11d

XXEtt−= −

∫

(8.127)

where

()Et is the age distribution function of the fluidized bed at the outlet; t*is

the complete reaction time of a single particle. For a single-layer fluidized bed, it