Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

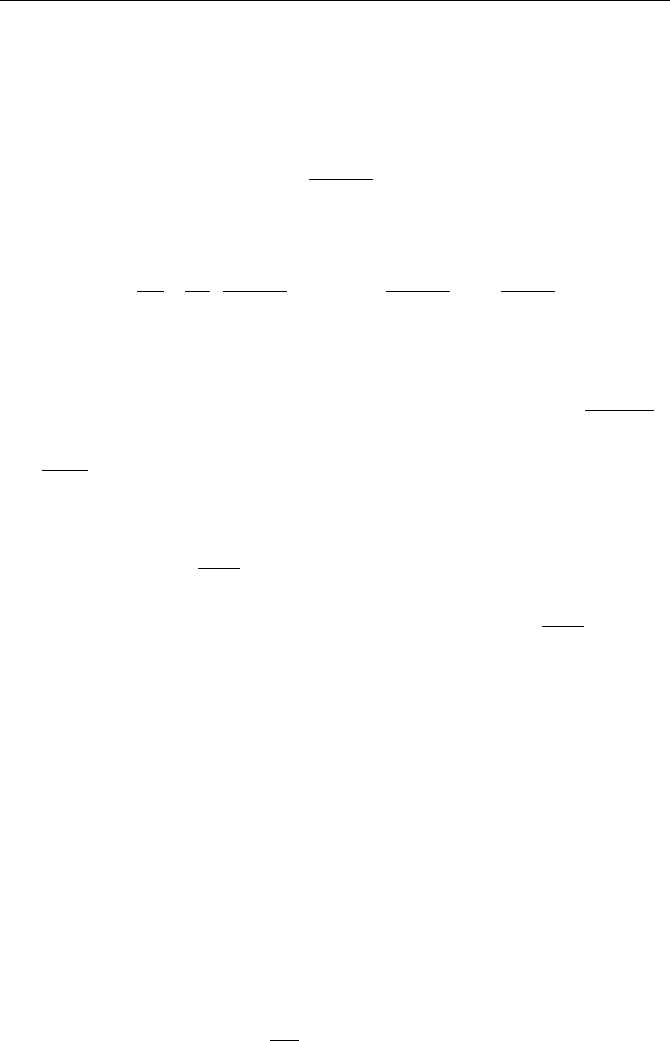
8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

8.2.3



Weibull probability distribution function

The Weibull distribution function can be expressed as follows:

min

1exp 1e

δδ

−

⎡⎤

⎛⎞

−

⎢⎥

=− − =−

⎜⎟

⎢⎥

⎝⎠

⎣⎦

(8.16)

Its more general form is

min min

mm m m

() exp e

DC CX

δδ δδ

δδ δ δ δ

−

⎡⎤

⎛⎞ ⎛⎞

−−

⎢⎥

== − =

⎜⎟ ⎜⎟

⎢⎥

⎝⎠ ⎝⎠

⎣⎦

(8.17)

where

min

is the minimal particle size;

is the specific particle size in the

group; C represents the dispersivity of the particle group;

min

δδ

−

=X ;

C = ; b is a constant,

= .

In order to obtain

C ,

−D curve can be linearized, so that

()

min m

lg ln lg lg lg

CXC C

δδ δ

⎛⎞

==−−

⎜⎟

−

⎝⎠

In the double log coordinates, the vertical axis represents

−

, and the

horizontal axis represents

min

− . Since

min

is assumed to be a known

value, it can be drawn as a straight line; and the constant

C can therefore be

obtained. This type of distribution function is not applicable to the particle

group if an appropriate value of

min

cannot be given to make it

linearized. Fig.8.5 is the diagram of Weibull probability distribution

function, in which the value of

C ranges from 1 to 3 for general industrial

bulks.

8.2.4



R-R distribution function (Rosin-Rammler distribution)

R-R distribution represents an extreme case of Weibull distribution, that is, when

min

()

1exp

=− − (8.18)

()

βδβδ

−==

−

exp

)(

(8.19)

  Chi Mei and Shaoduan Ou

where

= , therefore greater value of

indicates smaller size of the mean bulk

particles;

is equivalent to the particle size when 632.0

1 =−=

μm; n is the

distribution index, and the greater the value of

n , the narrower the distribution of

the particle size.

To obtain the constants

and n , linearization can be tried with the -D

curve by applying logarithm on both sides

lg ln lg lg

⎛⎞

=−

⎜⎟

−

⎝⎠

so that

and n are obtained by drawing a straight line with

D−

against

in the double log coordinates. If such a line is not available in

some specific cases, this specific bulk should be considered not applicable to

R-R distribution.

8.2.5



Nukiyawa-Tanasawa distribution function

The distribution pattern of the particle group formed by atomization is close to the

pattern described by the following model.

()

δδδ

−

⎟

⎠

⎞

⎜

⎝

⎛

exp

)(

(8.20)

where, the three constants,

a , b and n depend on the atomization condition.

Generally we take 1

<n , 2=a .

Fig. 8.5 Schematic of Weibull distributions

(a) Relationship among D, X and C ; (b) Relationship among

()

f , X and C

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

()

is a

function, and

()

δδ

−

∞

−

∫

=Γ

()

has the following characteristics:

()

()()

−Γ−=

+Γ

=Γ zz

() ( )

121 =

and

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

where

n and

are determined by Eq. 8.21and Eq. 8.22 using the arithmetic

average particle size

and the average volume of statistical surface area

measured by experimentally collected

N particles,

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

(8.21)

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

(8.22)

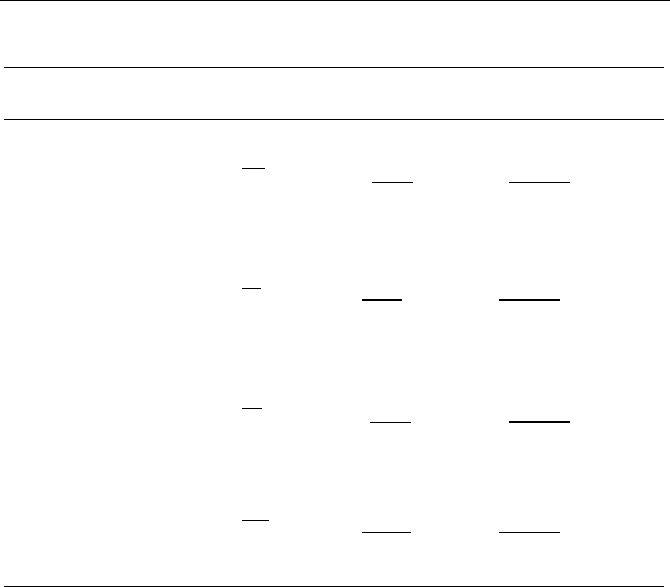
[Appendix] Statistical formula to calculate the average particle size

The formulas commonly used to determine the average particle size of the

particle group may have different definitions, according to the differences of usage

and applicable conditions. Their definitions and calculation formulas are listed in

Table 8.2.

Table 8.2 Calculation formulas of average particle size in particle groups

Name Symbol Definition Formula

Arithmetric mean diameter

∑

Surface-weighted mean diameter

∑

Mean surface diameter

1/2

⎛⎞

⎜⎟

⎝⎠

∑

1/2

⎛⎞

⎜⎟

⎝⎠

∑

  Chi Mei and Shaoduan Ou

Continues Table 8.2

Name Symbol Definition Formula

Mean volume diameter

1/3

⎛⎞

⎜⎟

⎝⎠

∑

1/3

⎛⎞

⎜⎟

⎝⎠

∑

Length-weighted

mean diameter

∑

Length-weighted mean

surface diameter

2/1

⎟

⎠

⎞

⎜

⎝

⎛

∑

1/2

⎛⎞

⎜⎟

⎝⎠

∑

Mass mean diameter

∑

Note: in this table,

n is the number of particles with size

in the sample; l ,

and v are

length, area and volume, respectively.

8.3



Dilute Phase Models

The study of the gas-particle two-phase flow is focused on analysis of the

movement of particle phase and the interactions between particle phase and gas

phase. Currently two major analytical methods are used (Cen and Fan, 1990; Zhou,

1994).

The first method is to take both gas and particle phases as continuous

media, and to investigate the flow behavior of the mixture phase in Euler

coordinates.The other method is to separate the particle phase from the gas

phase (continuous media), and to track the particle movement with

Lagrangian method.

The most frequently used gas-particle two-phase flow models are

summarized in Table 8.3.

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

Table 8.3 Common gas-particle two-phase models

Type Model name

Action of particles

on the fluid

Coordinates

system

Inter-phase

movement

Non-slip model Partially considered Euler No

Small-slip model Neglected Euler

Particle diffusion

relative to the fluid

Continuous

media

Multi-fluid model Considered Euler Yes

Discrete

media

Particle group

trajectory model

Considered Lagrangian Yes

8.3.1



Non-slip model

Non-slip fluid model is the simplest multi-phase fluid model. The following are

the major assumptions (Zhou,1994):

a) Time-averaged velocities of all particles are equal to the local fluid phase

velocities.

b) The particle phase is assumed to be continuous media with turbulent

diffusion, and the turbulent diffusivity is assumed to be equal to the diffusivity of

the fluid phase.

c) The interactions (momentum, heat and mass exchange) of particles

between different size levels and between the particle phase and fluid phase

are the same as the interactions between individual components in the fluid

mixture.

These assumptions indicate that the gas-particle two-phase flow is generally

considered as a single-phased fluid.

For the gas phase, the general conservation equation is:

()

ϕϕϕ

ϕρρϕ

⎟

⎠

⎞

⎜

⎝

⎛

∂

(8.23)

where

is a generally applicable variable;

Γ is the variable transfer

coefficient;

is the source term of gas phase;

S is the source term from

interactions between gas and particle phases. Parameters for different equations

are listed in Table 8.4.

  Chi Mei and Shaoduan Ou

Table 8.4 Parameters in the gas-phase equations of the single-phase model

Equation

Gas phase

continuity

0 0

Snm=−

∑

Gas phase

momentum

eff

iji

ρμ

∂

⎛⎞

∂∂

−+Δ+

⎜⎟

∂∂∂

⎝⎠

Gas phase turbulent

energy

eff

−

Turbulent

dissipation rate

eff

()

12k

CG C

εε

−

Gas phase species

eff

− sa

Gas phase enthalpy

eff

q−

nQ hs+

∑

In Table 8.4,

eff 0 T

μμμ

μρ

ijji

xxxx

⎡⎤

⎛⎞⎛ ⎞

∂∂

⎛⎞

∂∂

⎢⎥

=+++

⎜⎟⎜ ⎟

⎜⎟

⎜⎟⎜ ⎟

∂∂∂∂

⎢⎥

⎝⎠

⎝⎠⎝ ⎠

⎣⎦

Particle continuity equation or diffusion equation is:

()

eff

kj k k k

jjkj

vmnm

tx x x

ρν

⎛⎞

∂∂

+= +

⎜⎟

∂∂ ∂ ∂

⎝⎠

(8.24)

()

eff

jjkj

tx x x

⎛⎞

∂∂

⎜⎟

∂∂ ∂ ∂

⎝⎠

(8.25)

where

n and

m represent the density, particle number and mass of

the particle phase in group k , respectively;

is time changing rate of

m ;

eff

is the effective kinematic viscosity of gas phase,

()

eff 0 T

νμμ

=+;

is an empirical constant (Prandtl number) of particle diffusion, and is set at 1.0

here.

The solution method of the single fluid model (non-slip model) for gas-particle

two-phase flow is the same as that of the single-phase fluid equation, but with

additional continuity equations (similar to the diffusion equation of the gas species)

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

for the particle phase, and additional particle source terms in the gas phase

equations.

Simplicity is the major advantage of this model. However, the assumptions are

remarkably far from the realistic condition. Therefore, the differences between the

numerical predictions and the measurements are relatively large. That is why this

model is not widely used in engineering area hitherto.

8.3.2



Small slip model

The following are the major assumptions of this model (Cen and Fan, 1990; Zhou,

1994):

a) The particles are regarded as continuous media and are grouped by size. Each

group is a different phase possessing the same velocity

v , temperature

T ,

density

, and particle size

d .

b) The velocities of the particle groups are different, and are not equal to the

local gas velocity.

c) The time-averaged velocity of the particle group is the same as that of gas.

Because the velocity of slip is caused by turbulent diffusion of particles, the small

slip is also called turbulent drift.

d) The relationship between the multi-phase mixture and individual phase is

similar to that between multi-component fluid mixture and individual component

of the fluid.

The continuity equations of fluid phase and particle phase, the momentum, k ,

and energy equations and the expressions of S

and

in these equations are

the same as those for the non-slip model. The difference is the fluctuating velocity

component of the particle phase, which, according to the third model assumption,

should be the sum of the time averaged mixture velocity and the particle turbulent

diffusion component, namely

mpkjkj

vvv=+ (8.26)

where

v is the turbulent diffusion drift velocity of group k in the particle

phase. Then, the particle turbulent diffusion flux is

ppp pm

kj k kj k

JvD

ρρ

∂

==−

∂

(8.27)

Substitute it into the continuity equation of particle phase,

()()

mp mp m p m p

kkjk k

jjj

YYvD S

tx xx

ρρ ρ

⎛⎞

∂

∂∂ ∂

+= +

⎜⎟

∂∂ ∂∂

⎝⎠

(8.28)

where

Y is the mass concentration fraction of particle k .

In the non-slip model,

v represents the convection velocity, which is

  Chi Mei and Shaoduan Ou

represented by

v here.

The momentum equation of the fluid phase is:

() ()

gg gg g g g g rp gii

ii kii

jij

pv pv v pF f v S

tx xx

∂

∂∂ ∂

+=−++−+

∂∂ ∂∂

∑

(8.29)

The momentum equation of the particle phase is:

()()

pppp ppprpgp

kki kk

ki k

ikki kiik

jij

pv pv v pF f vS

tx xx

∂

∂∂ ∂

+=−++++

∂∂ ∂∂

(8.30)

where

and

are the partial pressure of gas and particle kth phase;

gji

τ and

kji

are viscous stress tensor;

and

are the volumetric force

component of the phases;

rpki

is the resistance of the kth phase particles to

the fluid

()

rp g p

ki i ki

fvv

=− (8.31)

where

is the residence time of the k th phase particle

= (8.32)

where

v and

are the kinetic viscosity and density of gas phase;

and

are the density and diameter of the

k th group particle.

The energy equation of the fluid is:

()()

g pg g g g pg g g pg g p k rg cgjj k

jjj

cT vcT ScT nQ Q Q

tx xx

ρρ λ

⎛⎞

∂

∂∂ ∂

+=+−−+

⎜⎟

∂∂ ∂∂

⎝⎠

∑

(8.33)

where

n is the particle number density of kth particle phase, number/m

;

Q is the heat removed by the kth phase particles from the fluid through

convection;

Sc T is the enthalpy change caused by the inter-phase mass

changes (S);

Q and

Q are the radiant heat and chemical reaction heat

of the gas phase, J/m

8.3.3



Multi-fluid model (or two-fluid model)

Unlike the previous two models (non-slip, small-slip), this model takes into

account not only the draft (turbulent diffusion) perpendicular to the main flow

direction of fluid, but also the time-averaged slip along the trajectories of the fluid

in the particle groups. The following are all expressed in its physical model.

 a) The particles are grouped by the initial size to form a number of particle

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

phases differing from each other in size. Each phase has its own velocity,

temperature and volumetric fraction.

b) Particle phases and fluid phase have their specific distributions of velocity,

temperature and volumetric density, etc. (field properties).

c) The differences between phase velocities are firstly due to the difference of

the initial momentums and secondarily due to the drifts caused by turbulent

diffusion.

d) The particles collision frequency rises as a result of enlarged volumetric

particle number concentration, which leads to the additional viscosity and

increased heat and mass transfer among particles.

The equations set for multi-fluid model is as follows:

a) Continuity equation of gas phase:

()

∂∂

(8.34)

b) Continuity equation of particle phases:

()

kkj k kj k

vvS

tx x

ρρ

∂

∂∂

+=− +

∂∂ ∂

(8.35)

()

kkj k kj

nv n v

tx x

∂

∂∂

+=−

∂∂ ∂

(8.36)

where

is the instant velocity of the kth phase, which can be represented as the

sum of the time averaged velocity

v and the fluctuation velocity '

v :

kj kj kj

vvv=+

(8.37)

According to Fick’s first law, the diffusion flux of particles is

()

kj k kj k kj kj k

Jv vvD

ρρ ρ

∂

== −=−

∂

(8.38)

where

f is the particle concentration fraction of the kth phase. Therefore, Eq.

8.35 can be written as

()

kkj k k k

jjj

vDnm

tx x x

ρρ

⎛⎞

∂∂

+=− +

⎜⎟

∂∂ ∂ ∂

⎝⎠

• (8.39)

c) Momentum equation of the gas phase:

() ()

()

geff

iji i

jjjij

ii kkiik

vvvp g

tx xxxx

vS F v v

ρρ μ ρ

ρτ

⎡⎤

⎛⎞

∂

∂∂ ∂∂ ∂

+=−+ +++

⎢⎥

⎜⎟

∂∂ ∂∂∂∂

⎢⎥

⎝⎠

⎣⎦

++ −

∑

(8.40)

d) Momentum equation of the particle phases:

  Chi Mei and Shaoduan Ou

()

k ki k kj ki k i k i ki

jkk

ki k k k

kk kj ki

jijjkij

nv nv v ng n v v

tx m

vvnn

nv v v

xxxx xx

⎛⎞

∂∂

+=+−++

⎜⎟

∂∂

⎝⎠

⎡⎤⎡ ⎤

⎛⎞ ⎛ ⎞

∂

∂∂∂

∂∂

++ +

⎢⎥⎢ ⎥

⎜⎟ ⎜ ⎟

∂∂∂∂ ∂∂

⎢⎥⎢ ⎥

⎝⎠ ⎝ ⎠

⎣⎦⎣ ⎦

(8.41)

e) Energy equation of the gas phase:

() ()

eff

ggg rρ gjj k

jjhj

hvh qnQhS

tx xx

ρρ

⎛⎞

∂

∂∂ ∂

+= −++

⎜⎟

∂∂ ∂∂

⎝⎠

∑

(8.42)

f) Species equation of the gas phase:

() ()

()

gs g s g s s g s

j j

jjj j

YvYD sYv

tx xx x

ρρ ρωαρ

⎛⎞

∂

∂∂ ∂ ∂

+= −+−

⎜⎟

∂∂ ∂∂ ∂

⎝⎠

(8.43)

where

is the time averaged reaction rate.

g) Energy equation of the particle phases:

()()

()

pphrpggp

'' '' ''

k kk kkj kk k k k k kk

j k

kk kj k kkj k k kk k kj

nc T nv c T n Q Q Q m c T c T

tx m

nc v T c v n T cTn v

∂∂

+=−−+−−

∂∂

∂

where

Q ,

Q and

Q are chemical, convection and particle radiation heat.

The above equation set contains such unknown variables as

vT,

nT, ''

nv and

''Yv , etc., which has to be closed through

simplification and modularization. The closed equation set can be solved

using IPSA method, a two-phase flow solver expanded from the SIMPLE

algorithm proposed by Patankar and Spalding. In the case of suspension

flow with low particle concentration, the PSIC method, as illustrated in Fig.

8.7, can be used.

Readers can refer to references (Cen and Fan, 1990; Zhou, 1994) for more

detailed discussions on continuous media multi-fluid models. The advantages

of the multi-fluid model is that the equations of both gas and particle phases

can be solved using the same numerical process, which results in more

detailed information about the particle phases without making extra

computational efforts. This model has been proven successful in predicting

pulverized coal combustion, gasification, 3D turbulence and swirling

gas-particle two-phase flow. Further investigations, however, are needed to

apply this model in breaking and aggregation processes where evaporation,

volatilization and phase change occur.

(8.44)