Mei C., Zhou J., Peng X. Simulation and Optimization of Furnaces and Kilns for Nonferrous Metallurgical Engineering

Подождите немного. Документ загружается.

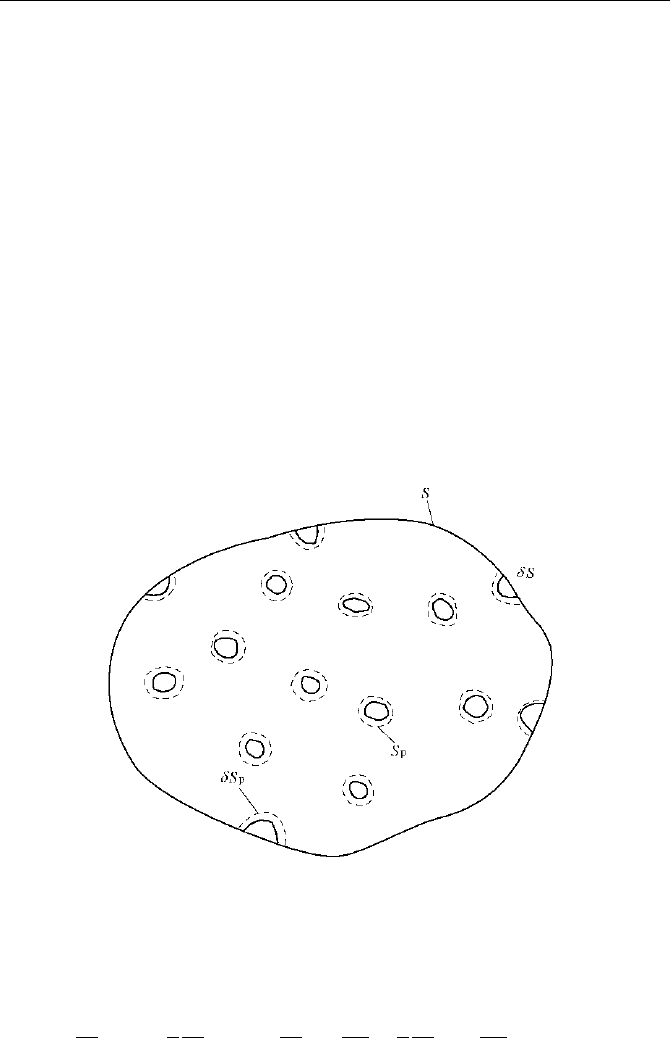
8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

8.3.4



Particle group trajectory model

Crowe and Smoot et al. brought up the conceptual model of particle groups in

1979 (Smoot and Partt, 1979). In this model a control volume with size

CV and

interface area

CS is defined as containing fluid and dispersed particle groups (also

called unit package), as shown in Fig. 8.6. Given that the surface area of a particle

S and the total interface area of the particle group ''SC , the model assumes

(Cen and Fan, 1990):

a) The gas phase is continuous whereas the particle phase is discrete.

The velocities and temperatures of the gas and particle phases are

different.

b)The particles are grouped according to their initial sizes and within the same

group all particles possess the same size, velocity and temperature.

c) Every particle group moves along the same trajectory. The model

follows up the changes on particle size, mass, velocity and temperature along

the trajectory.

Take the cylindrical reaction space in the presence of swirl-flow for example,

and the equation set governing the gas phase of the dispersed particle groups can

be written in a unified form as follows:

() ()

ϕϕϕϕ

ϕϕ

ϕρϕρ

rΓ

rrx

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

(8.45)

where

, Γ

, S

are listed in Table 8.5.

Fig. 8.6 Control unit of fluid and dispersed particle group

  Chi Mei and Shaoduan Ou

Table 8.5 Parameters in the gas-phase equations of the particle group trajectory model

Equation

Gas phase continuous 1 0 0

()

Smn

=⋅

∑

Axial momentum

eff

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

rrz

effeff

μμ

Suf

∑

⋅

Radial momentum v

eff

eff eff

eff

pu v

rz zrr r

μμ

μρ

∂∂ ∂ ∂ ∂

−+ + −

∂∂ ∂ ∂ ∂

⎛⎞⎛ ⎞

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

Svf

∑

⋅

Tangential momentum

eff

∂

−−−

eff

ωω

ωρ

∑

⋅

Turbulent kinetic

energy

eff

ρε

−

Dissipation rate of

turbulent kinetic

energy

eff

()

ρε

εε

CGC

−

Fraction of mixture

eff

0 0

Fluctuation value of f

eff

ρεμ

eff1

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

Fraction of the gas

mixture from particles

eff

0 S

Fluctuation value of

eff

ρε

ηη

eff1

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

Gas component

eff

−

Gas energy h

eff

−q

ppm

nQ cTS+

∑

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

In Table 8.5,

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

222

eff

f ,

f and

f in

S are the three components of the external force

imposed on the particle groups in unit volume. If the pressure gradient force,

virtual mass force, Basset force, Magnus force, Safman force, thermophoresis

force and gravity of the particles imposed by the gas flow are neglected, and only

the gas flow resistance is considered, then:

()

kz k

fuu

=−

()

kr k

fvv

=−

()

ωω

=−

where

is the particle relaxation time determined by Stokes’ resistance law,

μρτ

18/

r kkk

Table 8.6 lists the values of the constants obtained by numerical experiments.

Table 8.6 Values of the constants in Table 8.5

Constant



Value 0.09 1.44 1.92 2.8 2.0 0.9 0.9 0.9 0.9 0.9 0.9 1.3

Eq. 8.45 actually presents the generalized Navier-Stokes equation set, and can

be solved in the way of solving any simple fluid flow.

8.3.4.1



Trajectory of particle groups

Considering the trajectory of the particles in Lagrange coordinates, the motion

equation of a single particle is as follows:

()

pp p

Fmgv

= ∑ ++

(8.46)

where

∑ is the sum of all external forces imposed on this particle; gm

is the

gravity of the particle. The last term on the right side represents the inertia force

caused by the mass change of the particle.

It is actually rather difficult to consider in the model all the external forces imposed

on a particle. For industrial bulks, such as pulverized coal and concentrate particle, a

more practical approach is to start from modeling the most important facts and

gradually add up the complexity to get closer to the reality step by step.

If only the resistances of the particle are considered (including the inertial force

due to the mass change), particle motion equations in cylindrical coordinates will

  Chi Mei and Shaoduan Ou

be stated as:

()

⎪

⎭

⎪

⎬

⎫

−−=

+−=

guu

ωω

(8.47)

where

r is the radius of the particle position,

u ,

v and

are the axial,

radial and tangential velocity components respectively

Eq. 8.47 can be solved numerically. The particle trajectory can also be obtained

by Runge-Kutta integration method:

⎫

⎪

⎬

⎪

⎭

(8.48)

8.3.4.2



Computation of the particle source term

The particle groups may affect the gas-phase flow and in the mean time the gas

phase flow may also influence the trajectory and motion of the particle groups.

The coupling effect between the gas flow expressed by Euler’s equation and the

particles trajectory expressed in Lagrange equation is realized by the source term

(

When solving the particle motion by Lagrange method, every particle trajectory

represents the motion of a group of particles with the same size. The flow rate

expressed as the particl number of a group moving along the jth trajectory with

size of

ijijij

mmn

= (number/s) (8.49)

where

is the total flow rate of the particles;

is the mass of a single

particle.

When a particle passes through a computational cell k following trajectory

a particle mass source term is generated:

() ()()

ppp

out in

ij ij ij ij

mnm m

⎡⎤

=−

⎣⎦

(8.50)

The “out” and “in” in the subscripts represent the particle mass leaving and

entering cell k. n

keeps constant along the trajectory. The total particle mass

source term in cell k is:

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

ijkm

VmS

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∑∑

p,p

(kg/m

) (8.51)

where

∑

is the sum of the whole size group passing through cell k ;

∑

the sum of all particles with the same size but different initial position or trajectory

j .

Similarly, the source term in the momentum equation can be written as:

()()

p, pp pp

out in

u k ij ij ij ij ij

Snumum

⎧⎫

⎡⎤

=−

⎨⎬

⎣⎦

⎩⎭

∑∑

(kg/(m

gs)) (8.52)

()()

p, p p p p

out in

v k ij ij ij ij ij

Snvmvm

⎧⎫

⎡⎤

=−

⎨⎬

⎣⎦

⎩⎭

∑∑

(kg/(m

gs)) (8.53)

()()

p, p p p p

out in

w k ij ij ij ij ij

Snwmwm

⎧⎫

⎡⎤

=−

⎨⎬

⎣⎦

⎩⎭

∑∑

(kg/(m

gs)) (8.54)

The source terms in the energy equation of the particles include the heat effect

of reactions of the particles, the convection between particles and gas and the

radiation.

() ()

[]

ijij

ijkh

mmTCQn

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

−+−

∑∑

out

pp,p

(8.55)

where

Q is the convection and radiation heat transfer between particles and gas

in cell k.

The source terms for the turbulent energy and dissipation equations are usually

taken as zero.

Once the trajectories and the velocities on the trajectories of the particle groups

are determined by the Lagrange method, the particle concentration and velocity

fields can be solved by the volume average method.

For each computational cell, the total density of particle number can be

computed by the following equation:

()

ijijk

Vnn

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

ΔΔ=

∑∑

(number/m

) (8.56)

where

ijr

Δ is the residence time of the particle in the cell. Then the particle

volumetric concentration (or volumetric fraction) is:

()

ijijijkv

VvnC

⎥

⎦

⎤

⎢

⎣

⎡

ΔΔ=

∑∑

pr,

(8.57)

The particle velocity in this cell can be obtained by the momentum average

method:

  Chi Mei and Shaoduan Ou

()()

ijij

ijijijk

nvnv

⎥

⎦

⎤

⎢

⎣

⎡

ΔΔ=

∑∑∑∑

rpr,p

ττ

(m/s) (8.58)

8.3.5



Solution of the particle group trajectory model

A coupling method, called PSIC (particle-source-in-cell) for computing gas-particle

two-phase flow, was introduced by Crowe in 1977. The method can be used to predict

the relatively large slip between particle groups and the gas phase, as well as the changes

in size, velocity and temperature of the particle groups along the trajectories. PSIC is

simpler than IPSA. The computation procedure is shown in Fig. 8.7.

Fig. 8.7 PSIC computation scheme

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

8.4



Mathematical Models for Dense Phase

Generally, when the velocities of the gas flow passing through the bulk bed are

between the critical fluidization velocity (

u ) of the particle and the terminal

velocity (or carry out velocity,

u ), the bulk layer is considered to be a dense

fluidized bed. The Reynolds number

Re with respect to

u is determined

by the following experimental equation:

4.75

0.5

4.75

18 0.61

•

⎡⎤

⎣⎦

(8.59)

where

•

≡ (8.60)

()

ρρ

−≡

Ar (8.61)

where

is the void fraction of the fluidized system. For critical fluidized bed,

45.0~40.0=

in general. V

is the dynamic viscosity of gas phase Given

40.0=

, then

5.0

38.51400 Ar

= (8.62)

The gas flow velocity reaches the terminal sedimentation velocity when 1=

5.0

61.018 Ar

= (8.63)

where

•

≡ (8.64)

In the fluidized reactor, the overflow outlet divides the dense and dilute phase;

the fluid below this position is regarded as dense phase whereas that above is

regarded as dilute phase. Even though from the point of view of reactor designing,

the dense phase part and the dilute phases part should be considered as a unity

because they are both within the reaction zone, there are still large differences

between the dense and dilute phases in terms of fluidization condition, structural

features, transport properties and the major interests of researching.

The transport phenomena, either between the gas and particles in the dense

phase or between different bed layers, are very complicated, featuring high

fluctuation, randomicity and nonlinearity. The investigations in this area are still

far from enough and consensus still has to be reached regarding the understanding

and conclusions of the involved phenomena. Most of the published experiments

  Chi Mei and Shaoduan Ou

stay within the range of

dρ İ2.0kg/m

. Attempts to apply these data in practice

are subject to some limitations.

In this book only the frameworks of a few widely used physical models and

numerical solutions regarding dense phase reaction zone will be discussed.

Most of the currently available dense phase models focus on modeling the

bubbles’ structure, motion and change of sizes as well as correlating these

phenomena to variables about the fluidized beds. The major difference of

these models is basically the degree of complexity of the models and

correlations.

8.4.1



Two-phase simple bubble model

The following are the basic assumptions: (Chemical Engineering Handbook,

1989):

a) Gases flow through the bed layers either in bubble phase or in emulsion

phase. The gas velocity in emulsion phase equals the critical fluidized velocity

(

u ); the parts exceeding

u are considered in bubble phase.

b) The difference between the actual height of the bed layer (

L ) and the height

of critical bed layer is considered as filled with bubbles.

c) The change of the bubbles sizes and the influence of this change on other

variables in bed layer are negligible.

d) Chemical reactions only take place in the emulsion phase.

e) The exchange rate between the bubble phase and the emulsion phase is the

sum of penetration flow rate and the diffusion rate.

Based on the above assumptions and under the first-order chemical reaction

condition, the composition of the gas phase leaving the bed layer is as follows.

When emulsion phase is assumed to be fully mixed flow:

()

'1 e

−

+−

(8.65)

where

and

are respectively the concentrations of gas phase at the

outlet and inlet of the bed layer,

cmf r

0.5 0.25

fbb mf g b

0.5

'/ /

6.34

/1.3(/)

()

kkLukpWF

XQLuv u D gd

dgd

⎫

=−

⎪

⎬

⎪

⎡⎤

== +

⎣⎦

⎪

⎭

(8.66)

where

and

are the first-order reaction rate constants respectively based

on volume-concentration and weight-partial pressure of solid particles;

is the

8 Modeling of Dilute and Dense Phase in Generalized Fluidization 

total pressure;

is the catalyst weight;

is the total gas mole flow rate;

is the molecular diffusion coefficient of reactant gas;

is the equivalent bubble

size (diameter). The relative velocity

can be determined by the empirical

equation reported by Grace and Clift:

()

0.5

br b

0.711ugd= (8.67)

On the other hand, the assumptions of the present model indicate that the relative

velocity can also be expressed as:

br f mf mf f mf

fmf

()/()

uuu uu

=− =−

−

(8.68)

Joining the above two equations, the equivalent bubble size (

d ) can be estimated

as follows:

fmf mf

fmf

0.711

uu L

gLL

⎛⎞

−

⎜⎟

−

⎝⎠

• (8.69)

This is a model proposed in the early time for rough estimation of the bubbles in a

steady state bubble. Subsequent studies (Grace and Clift, 1974) reported that the

part of the gases flowing through the bed layer in the emulsion form (

uA• ) is

much greater than that predicted by this model (Cen et al.,1997).

8.4.2



Bubbling bed model

Based on the simple two-phase model, further assumptions are made that the

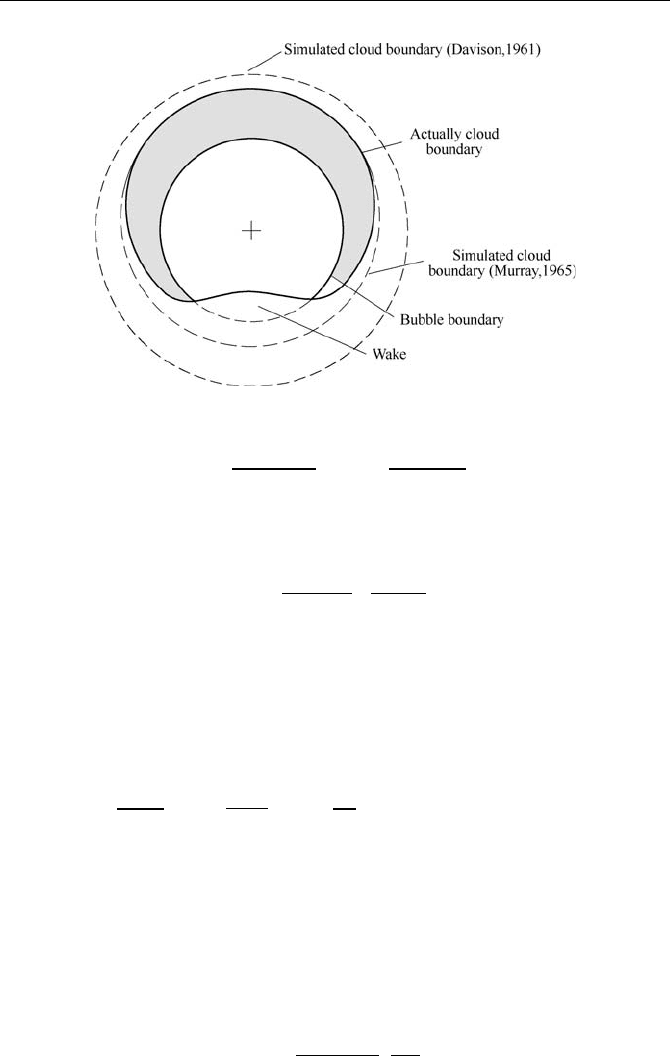
bubble phase contains bubble holes and bubble clouds (Fig. 8.8) surrounding

the bubbles, indicating. that the bed layer is composed of bubbles, bubble

clouds and emulsion phase. Similar to the simple two-phase model, it is still

assumed that the sizes of the bubbles do not change with the height of the bed

layer. The mass transfer between phases takes place only between bubble

clouds and emulsion phase. The transfers within gas phase take place between

the bubble holes and clouds as well as between the bubbles and the emulsion

phase (Kim and Han, 2007).

Under the first order reaction condition, the ratio between the compositions of

the bubble phase leaving and entering the bed layer is:

−

(8.70)

where

k is the mean overall mass transfer coefficient. Based on the above

assumptions,

k is expressed as(Kunii and Levenspiel,1969):

  Chi Mei and Shaoduan Ou

Fig. 8.8 Structure schematic of the bubble and bubble cloud

()

ss bc

fbt

ydF

kjSh

yd D

⎛⎞

⎜⎟

−

⎝⎠

(8.71)

where D is the mass diffusivity;

is the gas exchange coefficient between the

bubbles and the clouds (Davison and Harrison,1963):

0.5 0.25

1.25

4.5

5.85

−1

) (8.72)

where

is the ratio of the particle volume in the bubble holes to the volume of

the bubble holes;

is the ratio of the total volume of the holes to the total

volume of the bed layer;

is the Sherwood number, which is calculated based

on the terminal velocity of particles:

0.5 0.33

2.0 0.6Sh Re Sc=+

(8.73)

where,

Re =

where

is the logarithmic mean fraction of the non-diffusion component.

The bubbling bed model further assumes that the particles in the bubble clouds

are drawn into the wakes of the bubbles when the particles are moving downward.

Within the wakes, the particles are homogenously mixed with equal flow rates

while entering and leaving the wakes. This assumption allows us to estimate the

particle exchange coefficient

()

among the bubbles, the wakes of the

bubbles and the emulsion phase:

()

mf b

δε

•

−

≈

−

-1

) (8.74)