Медведева С.Н. Курс лекций Математические задачи в энергетике
Подождите немного. Документ загружается.

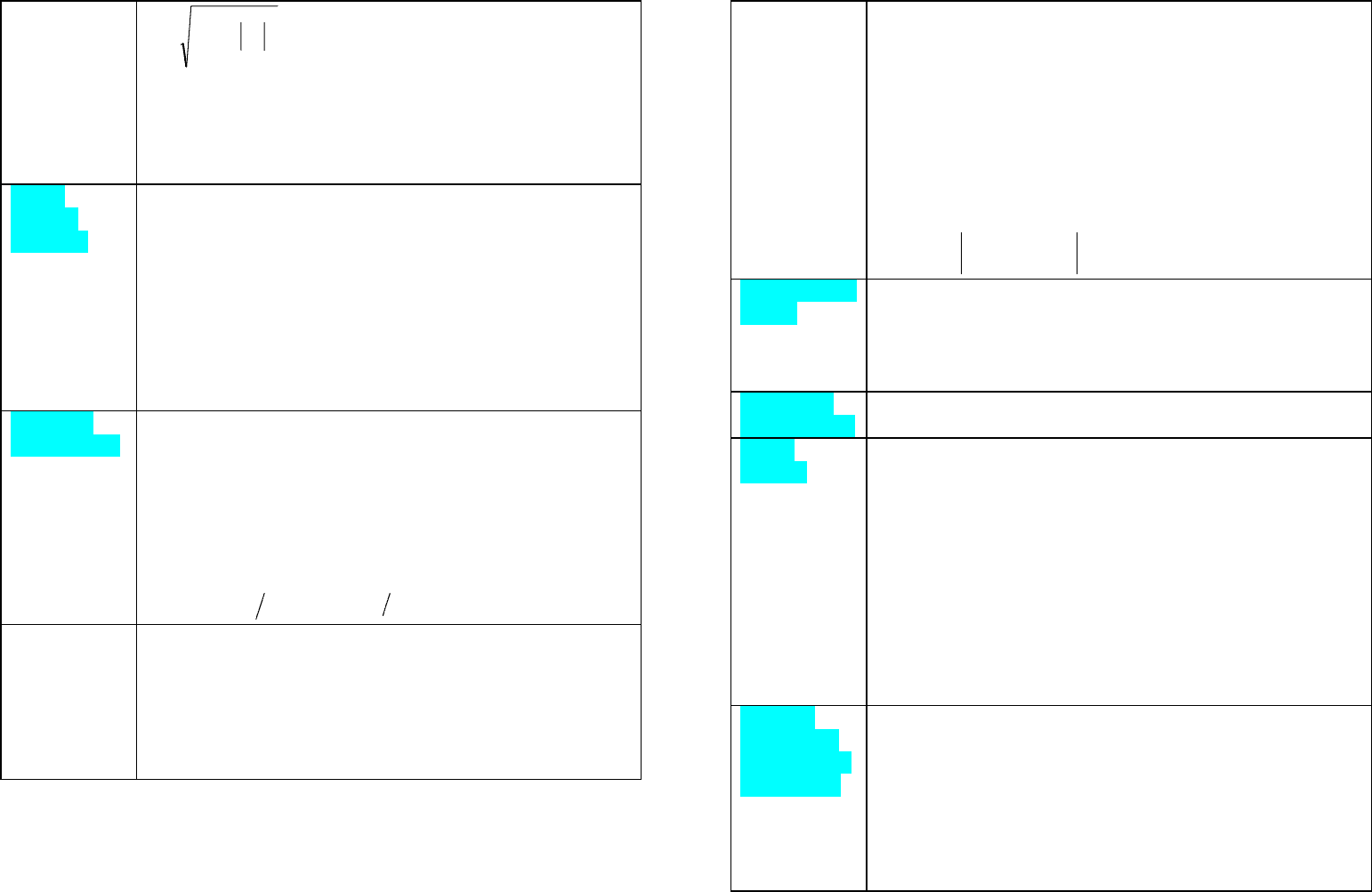
∏
∑
=
=
<Δ
n
i
n
j
ij
a
1
1
2
Почему? Некорректная постановка задачи, либо
специфичность рассматриваемой системы, например, при
расчете системы в УР на границе устойчивости.
Как избежать? В первом случае корректно поставить
задачу, во втором – решать ее другими методами
Метод
простой
итерации
Гораздо меньше операций на шаге итерации, но шагов
гораздо больше, чем
n. Были ограничения к применению
итерационных методов, когда был мал объем
оперативной памяти ЭВМ, но не сейчас.
Суть метода: задать любые исходные цифры, считая их
решением. Далее, подставив в уравнения, получить
уточненное решение. Полученные уточненные решения
снова подставить в уравнения для получения нового
уточнения до тех пор, пока не будет достигнута
заданная
точность
Алгоритм
метода ПрИт
1. представить каждое
k-е уравнение в виде решения
относительно
U
k
, т.е. из (20)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
++++=
++++=
++++=
nnnn
nn
nn
bUbUbU
bUbUbU
bUbUbU
0 ...
....
... 0
... 0
2211
221212
112121
, (22)
где
kkkjkj
aab
=
,
kkkk
aJb = .
Диагональные члены =0
2. Задать начальные приближения
)0(
1
U ,
)0(
2
U ,…,
)0(
n
U
3. Подставив начальные приближения в правую часть
уравнений (22), получим первое приближение. Таким же
образом результат может быть использован для
получения 2-го, 3-го и т.д. (
i+1)-го приближения
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
++++=
++++=
++++=
+
+
+
n
i
n
i
n
i
n
i
n
n
ii
i
n
n
ii
bUbUbU
bUbUbU
bUbUbU
0 ...
....
... 0
... 0
)(
2
2
)(
1
1
)1(
2
)(
2
)(
1
21
)1(
2
1
)(
1
)(
2
12
)1(
1
4. Процесс 3) закончить, если разность между соседними
приближениями всех величин достигнет заданной
точности
ε≤−
+ )()1( i
k
i
k
UU (23)
Общий вид
записи
k
n
kj
j
i
j
kjk
n
kj
i
j
kj
k
j
i
j
kj
i
k
bUbbUbUbU +=++=
∑∑∑
≠
=+=
−
=
+
1
)(
1
)(
1
1
)()1(
(24)
Матричная
форма записи
bBUU +=
+ )()1( ii
(25)
Метод
Зейделя
Суть: применить для расчета уже полученные на
k-м
шаге решения
k
n
kj
i
j
kj
k
j
i
j
kj
i
k
bUbUbU ++=
∑∑
+=
−
=
++
1
)(
1
1
)1()1(
(26)
или в матричной форме
bUBUBU ++=
++ )(
н
)1(
в
)1( iii
(27)
Вопросы
сходимости
итерационны
х процессов
Для выполнения условия (23) при любой точности
необходимо, чтобы
*
)(
lim
k
i
k
i
xx =
∞→
, (28)
где
*
i
x
– точные решения системы уравнений.
При выполнении условия (28) при любых начальных
приближениях итерационный процесс называется
сходящимся, иначе – расходящийся.
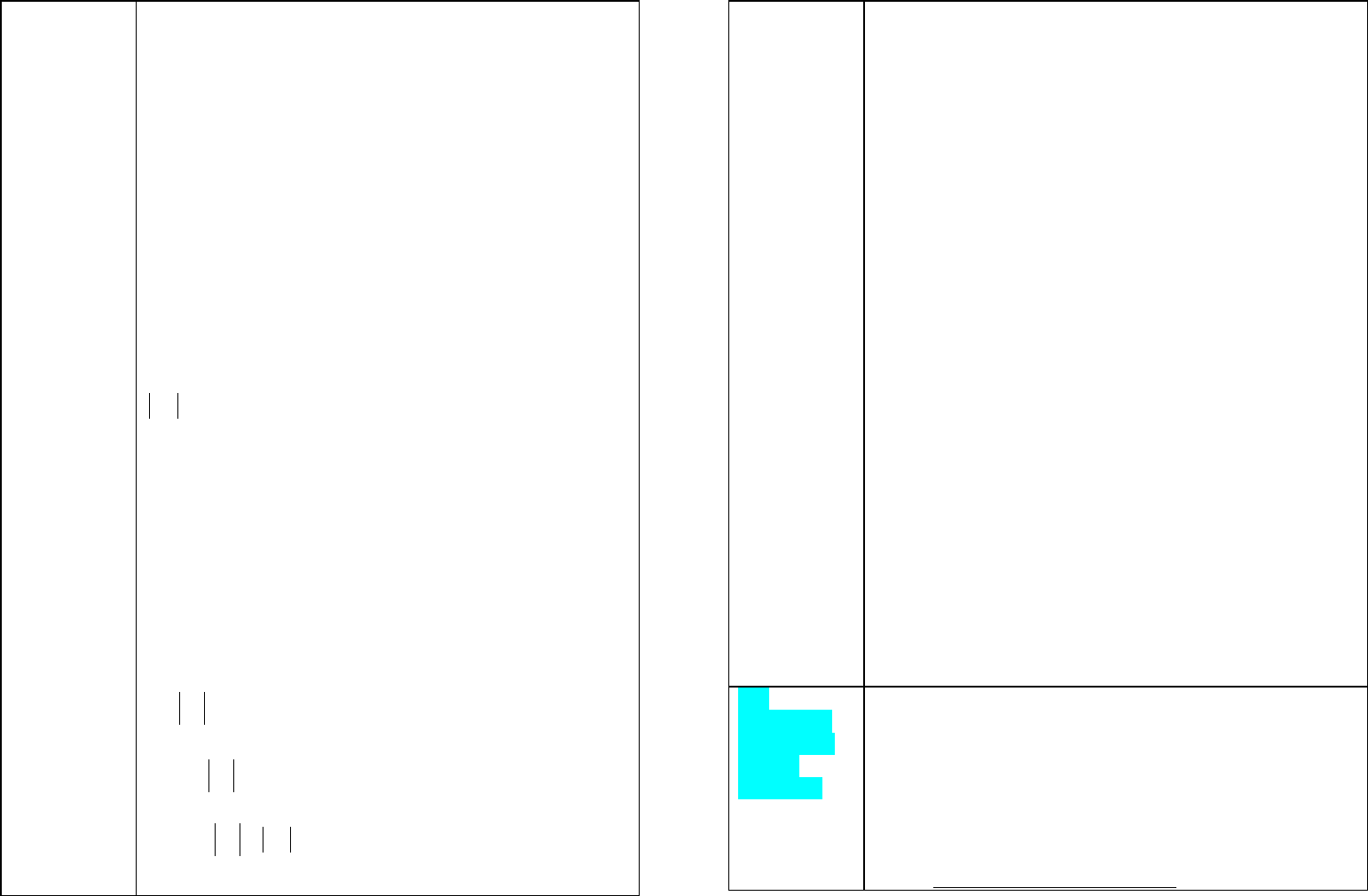
Выясним условия сходимости итерационного процесса.
Для метода ПрИт из (25), записав решение на (
i+1)-м и
i-м шаге, а затем вычтя решения, получим в матричной
форме
(
)
)1()()()1( −+
−=−
iiii
xxCxx (29)
Поскольку это выражение справедливо для любых
i, то
выражение (29) можно записать
(
)
)0()1()()1(
xxCxx −=−
+ iii
(30)
Условие сходимости (28) можно преобразовать к виду
(
)
0
)()1(
lim
=−
+
∞→
ii
i
xx
Тогда условие сходимости примет вид
0
lim
=
∞→
i
i
С (31)
Для выполнения условия (31)
необходимо и достаточно,
чтобы собственные значения матрицы
С были меньше 1.
nk
k
1,2,.., ,1 =<λ
Из курса ВМ вы знаете, что собственными значениями
матрицы называются корни характеристического
уравнения
0)det( =λ− 1C
или (записать в развернутом виде)
Вычисление собственных значений характеристического
уравнения более сложная процедура, нежели решение
системы уравнений методом Гаусса, поэтому
необходимыми и достаточными условиями на практике
не пользуются. Применяются
достаточные условия
сходимости
, которые формулируются непосредственно
через элементы матрицы С:
1
1
<
∑
=
n
j
ij
с при i=1,2,..,n
или 1
1
<
∑
=
n
i
ij
с при j=1,2,..,n
или
ii
n
ji
j
ij
aс <
∑
≠
=1
при i=1,2,..,n (32)
Элементы матрицы С применительно к методу узловых
напряжений определяются элементами матрицы узловых
напряжений и зависят только от ее свойств.
А из этих свойств
диагональный элемент не равен 0, т.е.
преобразование к виду (22) всегда выполнимо.
Кроме того, как правило,
диагональные элементы
превышают недиагональные
(св-ва матрицы узл.
проводимостей), но поскольку в схемах замещения
имеются ветви с
индуктивными и емкостными
проводимостями
, то условие (32) часто не выполняется.
Однако, условие (32) –достаточное, поэтому его
невыполнение не означает, что итер. процесс не сходится
, в действительности итер. процесс по методу простой
итерации обычно сходится, хотя и очень медленно.
По методу Зейделя необходимые и достаточные условия
будут отличаться от необходимых и достаточных
условий по методу простой итерации, поскольку иначе
формируется матрица С, состоит из 2-х частей. Поэтому
в общем случае могут быть системы уравнений, которые
сходятся по методу Зейделя, и не сходятся по методу
ПрИт.
Но опять мы не будем пользоваться необх. и
дост.
условиями из-за их сложности.
Достаточные условия сходимости метода Зейделя
совпадают с достаточными условиями сходимости
метода ПрИт, но скорость сходимости процесса по
методу Зейделя больше, т.е. сходится быстрее.
Как
обеспечить
сходимость
итерац.
процесса?
Итак, как по методу Зейделя, так и по методу ПрИт мы
не всегда можем получить решение, поскольку процесс
может расходиться.
Но даже простое переставление уравнений в исходной
системе может изменить условия сходимости. Поэтом
возникает вопрос,
нельзя ли преобразовать исходную
систему уравнений таким образом, чтобы процесс
обязательно сходился
?
При положительно-определенной
матрице итерац.
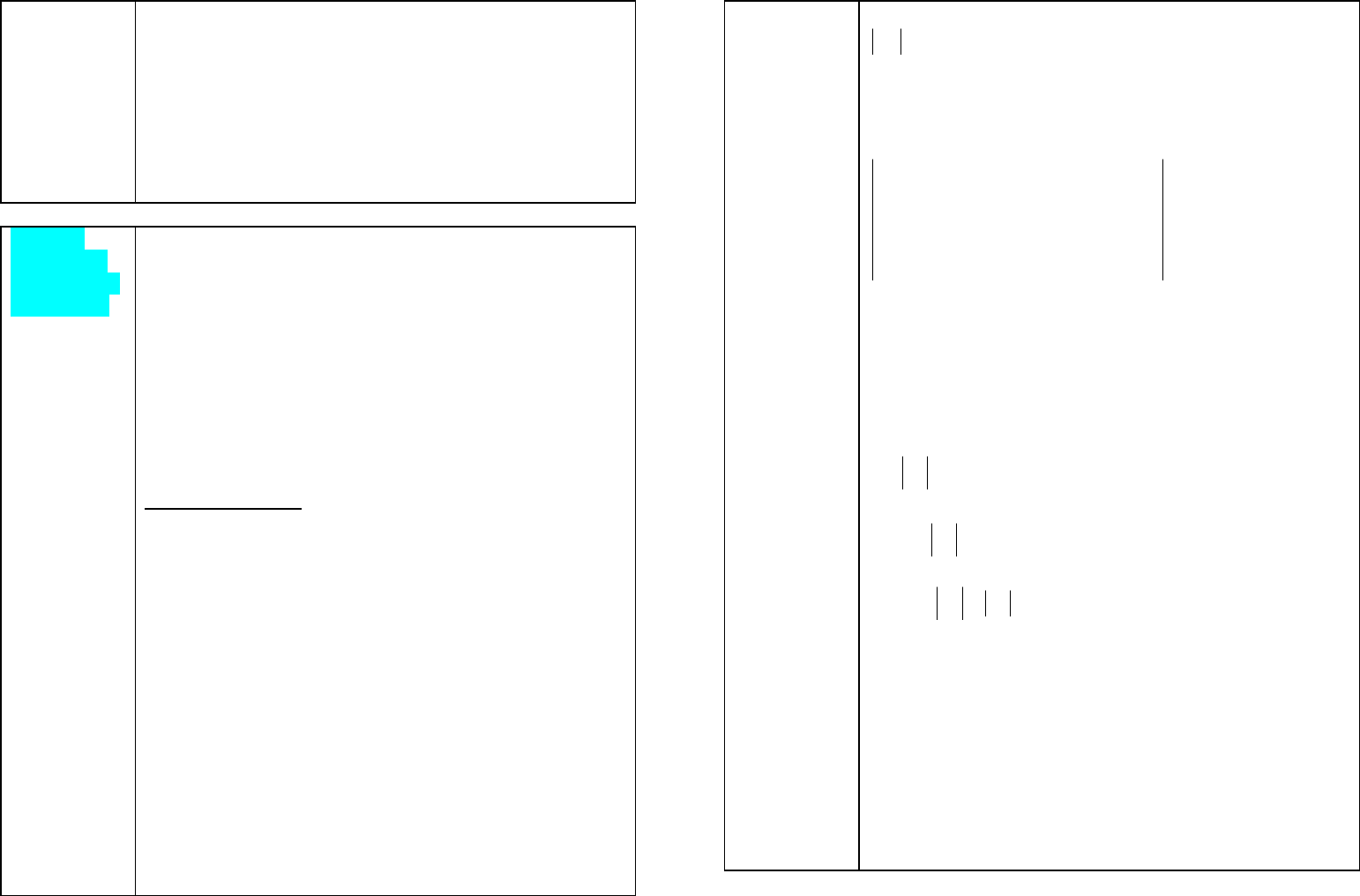
процесс по методу Зейделя сходится всегда.
Чтобы привести исходную матрицу к положительно-
определенной, надо исходную систему уравнений
умножить слева на транспонированную матрицу
коэффициентов, т.е. если имеем систему
Ах=b, то умножив на A
t
, имеем A
t
Ax=A
t
b – или
A'x=b', матрица A' – положительно определенная,
итерационный процесс по методу Зейделя обязан
сходиться. (медленно!, вырастает объем вычислений)
Вопросы
сходимости
итерационны
х процессов
Для выполнения условия (23) при любой точности
необходимо, чтобы
*
)(
lim
k
i
k
i
UU =
∞→
, (28)
где
*
i
U – точные решения системы уравнений.
При выполнении условия (28) при любых начальных
приближениях итерационный процесс называется
сходящимся, иначе – расходящийся.
Выясним условия сходимости итерационного процесса.
Для метода ПрИт из (25), записав решение на (i+1)-м и
i-м шаге, а затем вычтя решения, получим в матричной
форме
(
)
)1()()()1( −+
−=−
iiii
UUBUU (29)
Поскольку это выражение справедливо для любых
i, то
выражение (29) можно записать
(
)
)0()1()()1(
UUBUU −=−
+ iii
(30)
Условие сходимости (28) можно записать в виде
(
)
0
)()1(
lim
=−
+
∞→
ii
i
UU
Тогда условие сходимости (30) примет вид
0
lim
=
∞→
i
i
В , (31)
потому что на первом шаге итерации, как правило, нуль
не получается
Для выполнения условия (31)
необходимо и достаточно,
чтобы собственные значения матрицы В были меньше 1.
nk
k
1,2,.., ,1 =<λ
Из курса ВМ вы знаете, что собственными значениями
матрицы называются корни характеристического
уравнения
0)det(
=
λ
−
1B
или в развернутом виде
(
)
()
()
0
...
.........
...
...
21
22221
11211
=
λ−
λ−
λ−
nnnn
n
n
bbb
bbb
bbb
Вычисление собственных значений характеристического
уравнения более сложная процедура, нежели решение
системы уравнений методом Гаусса, поэтому
необходимыми и достаточными условиями на практике
не пользуются. Применяются
достаточные условия
сходимости
, которые формулируются непосредственно
через элементы матрицы
В:
1
1
<
∑
=
n
j
ij
b при i=1,2,..,n
или 1
1
<
∑
=
n
i
ij
b при j=1,2,..,n
или
ii
n
ji
j
ij
bb <
∑
≠
=1
при i=1,2,..,n (32)
Элементы матрицы B применительно к методу узловых
напряжений определяются элементами матрицы узловых
напряжений и зависят только от ее свойств.
А из этих свойств
диагональный элемент не равен 0, т.е.
преобразование к виду (22) всегда выполнимо.
Кроме того, как правило,
диагональные элементы
превышают недиагональные
(см. свойства матрицы
узловых проводимостей), но поскольку в схемах
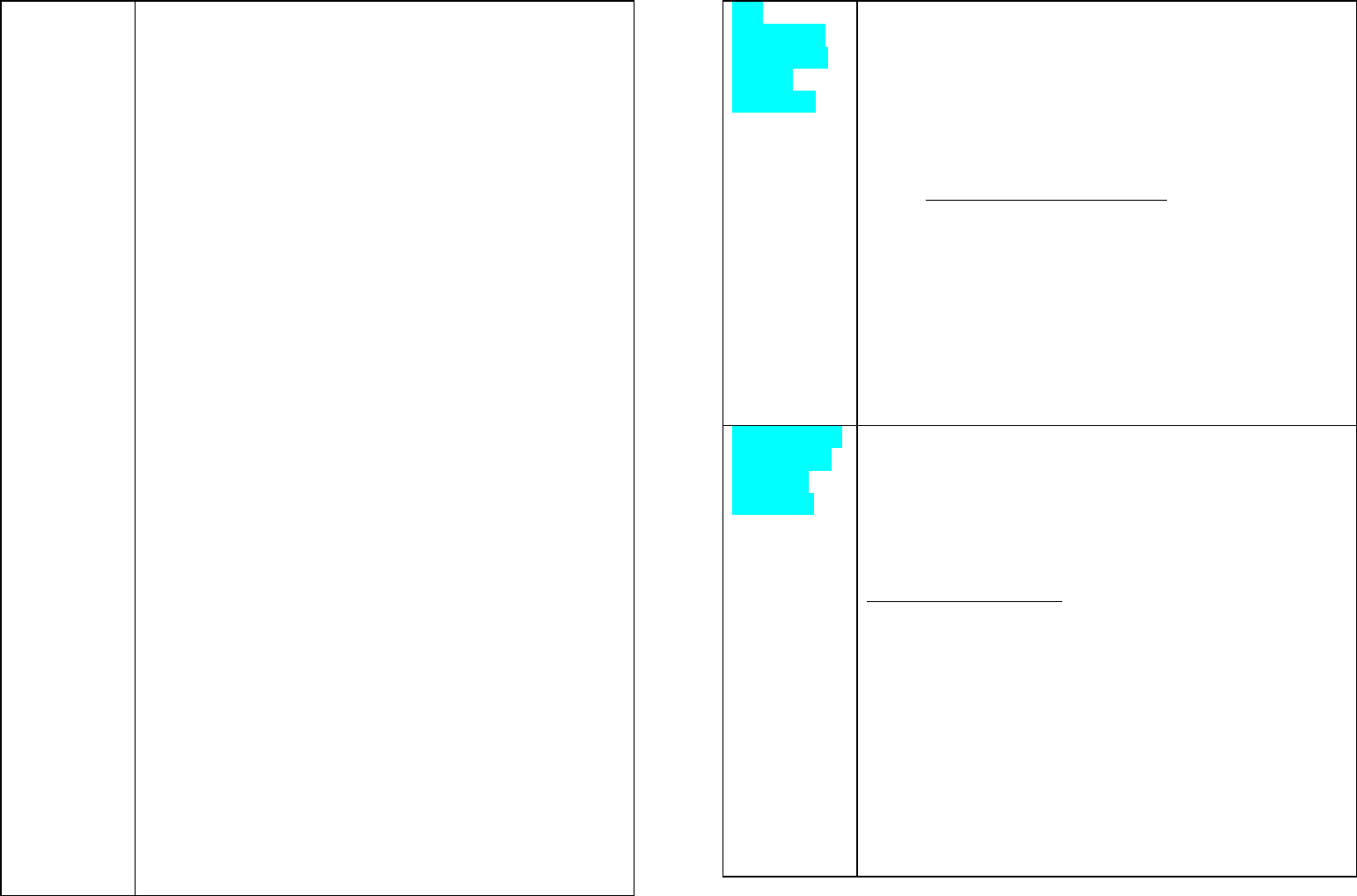
замещения имеются ветви с индуктивными и
емкостными проводимостями
, то поскольку емкостная
проводимость может быть отрицательной, условие (32)
часто
не выполняется.
Однако, условие (32) –достаточное, поэтому его
невыполнение не означает, что итерационный процесс не
сходится , в действительности итерационный процесс по
методу простой итерации обычно сходится, хотя и очень
медленно.
Для исследования сходимости
по методу Зейделя
представим итерационный процесс в виде
bUBUBU ++=
− )1(
в
)(
н
)( iii
, (33)
где В
н
и В
в
– верхняя и нижняя треугольные матрицы.
Выражение (33) можно преобразовать
(
)
() ()
;11
;1
1
н
)1(
в
1
н
)(
)1(
вн
)(
bBUBBU
bUBBU
−
−
−
−
−+−=
+=−
ii
ii
или
b'UB'U +=
− )1()( ii
(34)
Выражение (34) аналогично выражению (25) для метода
простой итерации, т.е. для сходимости по методу Зейделя
необходимые и достаточные условия формируются
аналогично условиям по методу простой итерации через
определение собственных значений матрицы. Поскольку
сами матрицы отличаются, то будут отличаться и
условия сходимости. И в общем случае могут быть
системы уравнений, которые сходятся
по методу
Зейделя, и не сходятся по методу ПрИт.
Но опять мы не будем пользоваться необходимыми и
достаточными условиями из-за их сложности.
Достаточные условия сходимости метода Зейделя
совпадают с достаточными условиями сходимости
метода ПрИт, поскольку матрица узловых
проводимостей формируется так же и обладает теми же
свойствами, но скорость сходимости процесса по методу
Зейделя больше, т.е. сходится быстрее.
Как
обеспечить
сходимость
итерац.
процесса?
Итак, как по методу Зейделя, так и по методу ПрИт мы
не всегда можем получить решение, поскольку процесс
может расходиться.
Но даже простое переставление уравнений в исходной
системе может изменить условия сходимости. Поэтому
возникает вопрос,
нельзя ли преобразовать исходную
систему уравнений таким образом, чтобы процесс
обязательно сходился
?
При положительно-определенной
матрице итерац.
процесс по методу Зейделя сходится всегда.
Чтобы привести исходную матрицу к положительно-
определенной, надо исходную систему уравнений
умножить слева на транспонированную матрицу
коэффициентов, т.е. если имеем систему
Ах=b, то умножив на A
t
, имеем A
t
Ax=A
t
b – или
A'x=b', матрица A' – положительно определенная,
итерационный процесс по методу Зейделя обязан
сходиться. (медленно!, вырастает объем вычислений)/
(Замечания к выполнению курсового.)
Математичес
кий аппарат
Microsoft
MathCAD
Чтобы понять вычислительные процессы, надо их
прорешать вручную, составить программу, "пощупать".
А для практического решения реальных задач, в которых
число уравнений порядка сотен, надо использовать
современные средства.
Mapple, MathLAB, MathCAD.
MathCAD под Windows
.
– работа с файлами;
– возможности внесения и форматирования
пояснительного текста;
– на панели инструментов дополнительные клавиши:
Insert Function — вставка функции, Insert Utit –
вставить единицы измерения,
Calculate - пересчитать;
– дополнительно
математическая панель, в ней:
арифметическая панель, панель логических операций
и операций сравнения, графики, матрицы, элементы

матанализа (интегралы, производные), панель
программирования (внутренний язык Си++)
– последовательность операций.
