Медведева С.Н. Курс лекций Математические задачи в энергетике
Подождите немного. Документ загружается.

План Содержание
ПРИМЕР
e
e
a
a
c
c
d
b
b
1
2
3
4
5
6
I
I
I
I
II
E
1
Z
1
Z
2
I
1
I
4
I
b
I
c
I
5
I
e
I
2
I
a
E
2
Z
4
Z
6
E
6
I
6
Z
5
Z
3
I
d
E
5
I
3
E
4
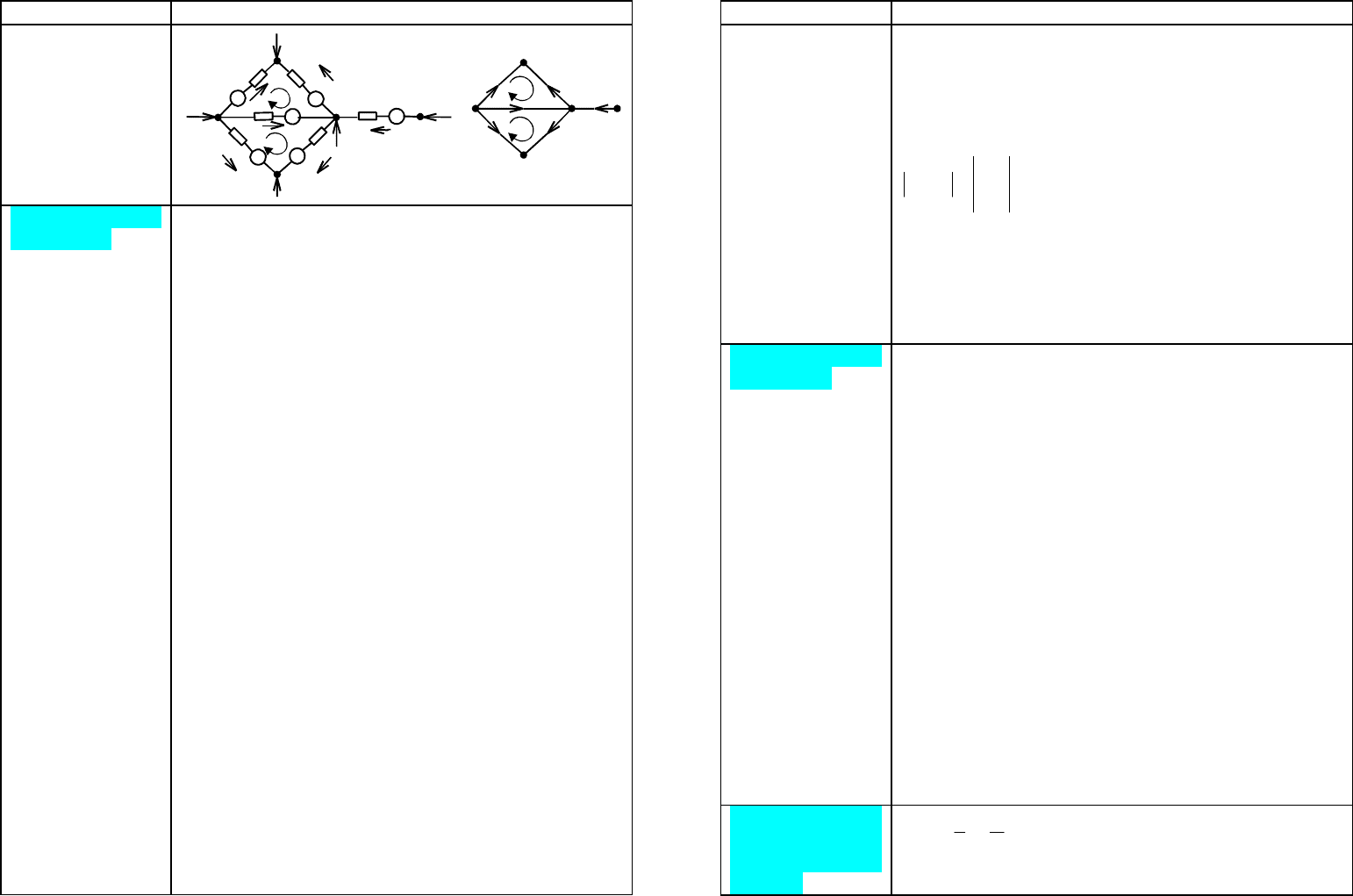
Первая матрица
инциденций
Элементы
Пример
Свойства
Балансир. узел
=матрица соединений ветвей в узлах, число строк
которой = числу вершин графа, а число столбцов =
числу ребер
(
)
mjnimM
ij
,..,1 ;,..,1 ,
=
=
=
∑
номера строк соответствуют номерам вершин
(узлов), номера столбцов – номерам ребер (ветвей)
1
+
=
ij
m
, если узел i является начальной вершиной
ветви j,
1
−
=
ij
m
, если узел i является конечной вершиной
ветви j,
0
=
ij
m
, если узел i не является вершиной ветви j.
654321
011001
000100
110110
101000
000011
e
d
c
b
a
M
−−
−−
−
−
=
∑
1) каждая строка показывает, какие ветви
подсоединены к узлу схемы
2) каждый столбец показывает, какие узлы соединяет
эта ветвь – отсюда в каждом столбце одна 1, одна –1,
остальные 0, т. .е. сумма всех строк матрицы по
столбцам должна давать нулевую (строчную)
матрицу
0=
∑
Mn
t
, где n
t
–единичная строка.
План Содержание
Выделим строку, соответствующую
балансирующему узлу, будем считать,
что это последний узел, тогда
01
б
=×
M
M
n
t
, откуда М
б
=-n
t
M
М– матрица соединений для схемы без бал.узла, М
б
–
для бал. узла. Отсюда следует, что по матрице М
может быть получена строка для балансирующего
узла, а значит полная матрица соединений, т. е.
восстановлена вся схема соединений
Вторая матрица
инциденций
Элементы
Пример
Свойства
= матрица соединений ветвей в независимые
контуры, число строк которой равно числу
независимых контуров k, а число столбцов = числу
ветвей m
(
)
mjkinN
ij
,..,1 ;,..,1 ,
=
=
=
1
=
ij
n
, если ветвь входит в контур и их
направления совпадают;
1
−
=
ij
n , если ветвь входит в контур и их
направления противоположны;
0
=
ij
n
, если ветвь не входит в контур
654321
111000
010011
II
I
N −
−
−
=
Каждая строка матрицы показывает, какие ветви
входят в контур, каждый столбец – в состав каких
контуров входит ветвь
Законы Кирхгофа
в матричной
форме через
матрицы
1:
JIM
=
, где I,J – вектор-столбцы токов в ветвях
и задающих токов в узлах. (матрица m×n)
План Содержание
инциденций
2:
0
в
=UN , где
в
U – вектор-столбец падений
напряжений в ветвях
Получение
обобщенного
уравнения
состояния
Используя з-н Ома для сети произвольной
конфигурации, содержащей m ветвей, между
которыми отсутствует взаимноиндуктивная связь (но
можно ее и учесть, см. предыд. лекцию), а именно
EIZU −
=
вв
, где
(
)
miZZ
i
,..,1 ,diag
в
=
=
–
диагональная матрица сопротивлений ветвей, Е –
столбец ЭДС в ветвях
Подставляя во второй з-н Кирхгофа, получаем
(
)
0
в
=
−
EIZN или
кв
EIZN
=
, где
к
Е –
столбец контурных ЭДС, представляющих собой
алг. сумму ЭДС ветвей, входящих в каждый
независимый контур.
Объединяя последнее уравнение и ур-ние по 1 з-ну
Кирхгофа, получим систему уравнений состояния эл.
цепи
⎭
⎬
⎫
=
=
кв
EIZN
JIM
Если матрицы М и NZ
в
рассматривать как блоки
объединенной матрицы параметров схемы
замещения
в
NZ
M
A =
, а матрицы J и E
к
как блоки
объединенной матрицы исходных параметров
режима
к
E
J
F =
, то получим обобщенное уравнение
состояния
FIA
=
Рассуждения по
формированию
обобщенного
уравнения
Составление матрицы М
Σ
для схемы любой
сложности не представляет труда. Для этого
достаточно пронумеровать все узлы и ветви схемы
замещения и в каждом столбце матрицы М
Σ
записать
«+1» «-1» в тех строках, которые соответствуют
План Содержание
соединяемым данной ветвью узлам, а в остальных
элементах этого столбца записать «0». Выбор того
или иного варианта произволен и в итоге определяет
направление k-й. ветви.
Вычеркивая из полученной матрицы М
Σ
строку,
соответствующую выбранному балансирующему
узлу, получаем искомую матрицу М.
Составить матрицу N для сложных электрических
систем в отличие от матрицы М затруднительно,
поскольку предварительно требуется выделить
независимые контуры, количество которых k =т-n+1
может быть значительным.
Сравним способы формирования уравнений
состояния электрической цепи
1) непосредственно по ее схеме и по з-
нам Кирхгофа
2) в обобщенной форме с использованием матриц М
и N
По трудоемкости оба способа примерно равноценны,
Основная трудность заключается в составлении
уравнений для независимых контуров в первом
случае и матрицы N – во втором.
Очевидно, что в варианте 1) эта трудность
принципиально неустранима, тогда как в варианте 2)
ее можно избежать, если формализовать
процесс
составления матрицы N. Возможность такой
формализации обусловлена тем, что матрица М
содержит в себе исчерпывающую информацию о
конфигурации схемы, в том числе и необходимую
для составления матрицы N.
Для реализации этой возможности необходимо
установить аналитическую зависимость,
связывающую матрицы М и N.
Вывод
аналитической
зависимости
матриц М и N
Обозначим столбец напряжений всех узлов схемы
(узловых напряжений) как U
Σ
=(U
i
), i=l, ..., п.
Используем свойство матрицы
М
Σ
, а именно то,
каждый столбец матрицы М
Σ
имеет положительную
единицу на месте начальной вершины и
отрицательную – на месте конечной вершины ветви.
План Содержание
Поэтому достаточно транспонированную матрицу
соединений
М
Σt
умножить справа на столбец
узловых напряжений
U
Σ
, чтобы получить столбец
разностей напряжений по концам каждой ветви, т. е.
падений напряжений на ветвях:
U
В
= М
Σt
U
Σ
(1)
Пример:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+−
+−
+−
+−
+−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
∑∑
cb
ec
dc
ca
ea
e
d
c
b
a
t
UU
UU
UU
UU
UU
U
U
U
U
U
UM
00110
10100
10010
01100
00101
10001
Здесь матрица узловых напряжений U
Σ
записана для
всех узлов схемы (включая балансирующий). При
этом узловые напряжения могут быть определены
относительно любого узла.
Узловые напряжения целесообразно определять
относительно балансирующего узла, т. е. как
падения напряжения от каждого из независимых
узлов схемы до балансирующего. Тогда можно
выделить вектор-столбец, связанный с напряжением
балансирующего узла и записатьравенство
U
Σ
- U
б
n=
⎥
⎦
⎤
⎢
⎣
⎡
∇
0
U
,
где n—единичный столбец (при этом
балансирующий узел предполагается последним по
номеру, т. е.
U
б
=U
n
. Здесь матрица U
∇
=(U
i
-U
б
),
i=1,…, n-1
определяет напряжения узлов
относительно балансирующего.
Подставим в (1)
План Содержание
U
В
=М
Σt
⎥
⎦
⎤
⎢
⎣
⎡
∇
0
U
=[M
t
M
бt
]×
⎥
⎦
⎤
⎢
⎣
⎡
∇
0
U
=M
t
U
∇
. (2)
Подставим полученное выражения для падений
напряжений на ветвях в матричное уравнение
второго закона Кирхгофа получим
, NM
t
U
∇
=0
Поскольку это условие справедливо при любой
матрице U
∇
, то NM
t
=0 (*)
Полученное выражение отображает общее
топологическое свойство графа, но вместе с тем оно
не позволяет непосредственно определить матрицу
N по известной матрице М. Это связано с тем, что
одной и той же электрической цепи в общем случае
соответствует несколько различных систем
независимых контуров, или, иными словами, одной
и той же матрице
М можно поставить в соответствие
несколько матриц N.
Однозначность в выделении системы независимых
контуров, позволяющая получить матрицу N по
матрице М, может быть достигнута при
использовании таких понятий теории графов, как
дерево и хорды.
Дерево Деревом называется наименьший связанный
подграф, содержащий все вершины графа. Такой
подграф не содержит контуров. Иными словами,
дерево – это разомкнутая часть замкнутой схемы,
которая соединяет все ее узлы. Число ветвей,
входящих в состав дерева схемы, на единицу меньше
числа узлов всей схемы (m
Д
=n-1). Меньшим числом
ветвей нельзя соединить те же узлы.
Хорда Ветви, не вошедшие в дерево схемы, называются
хордами. Число хорд равно числу независимых
контуров схемы
(m
x
=m- m
Д
=m-n+1=k). Подграф,
состоящий из хорд, может содержать контуры; он
может получиться и несвязанным.
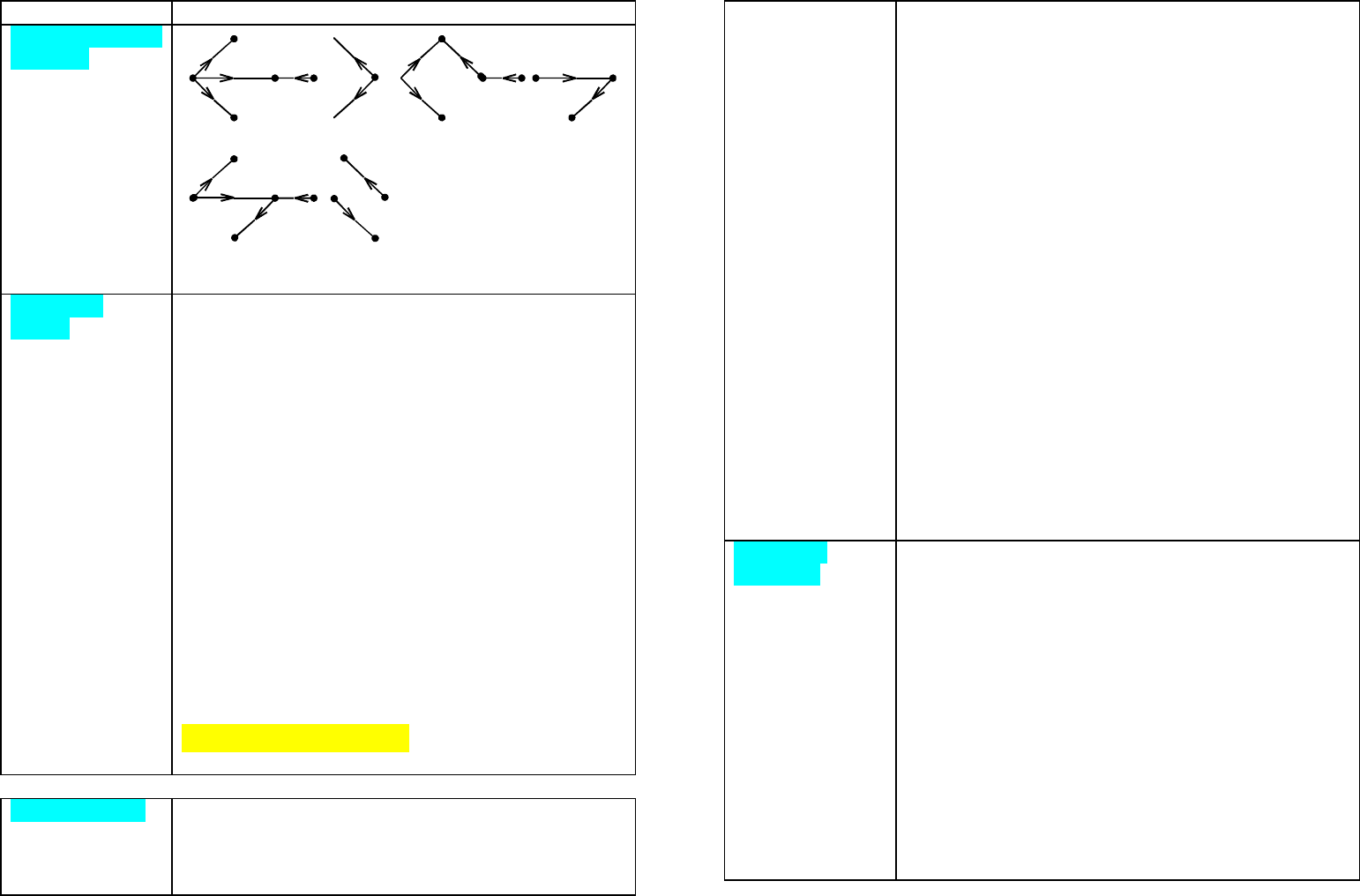
План Содержание
Примеры для той
же схемы
e
e
e
e
a
a
a
a
a
c
c
c
c
c
c
d
d
d
b
b
bb
bb
b
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
Одна и та же схема может быть разделена на дерево
и хорды по-разному
Разделение
матриц
В результате матрица М, записанная первоначально
при произвольной нумерации ветвей, путем
перестановки столбцов преобразуется к виду
M=[M
α
M
β
], где M
α
–подматрица (блок),
относящаяся к дереву схемы;
M
β
– подматрица,
характеризующая подграф, состоящий из хорд.
Аналогично можно разделить на блоки и матрицу N:
N=[N
α
N
β
]
Подставив два последних выражения в выражение
(*), получим
[N
α
N
β
]×
⎥
⎦
⎤
⎢
⎣
⎡
β
α
t
t
M
M
= N
α
M
αt
+ N
β
M
βt
=0 (2)
Матрица M
α
, а следовательно и M
αt
, является
квадратной порядка (n-1) и неособенной. Поэтому,
умножая справа обе части выражения (2) на
M
αt
-1
найдем
N
α
= - N
β
M
βt
M
αt
-1
(**)
Доп. упрощение
Таким образом, если известны M
α
, M
β
и N
β
, то
можно определить N
α
, а следовательно, и всю
матрицу N. Матрицу N
β
можно задать равной
единичной матрице (N
β
=1).Это соответствует
выбору системы таких контуров, которые
характеризуются следующими свойствами:
–каждый из контуров замыкается одной хордой, т. е.
каждая хорда входит только в один контур;
–последовательности нумерации хорд и контуров
одинаковы;
–направления обхода контуров и замыкающих их
хорд совпадают. Рассмотренные контуры
называются базисными. Они являются взаимно
независимыми, так как в каждый
из них входит одна
ветвь (хорда), не входящая ни в какой другой контур.
Таким образом, при выделении базисных контуров
выражение (**) преобразуется к виду
N
α
=- M
βt
M
αt
-1
Итак, разделение матрицы М на блоки,
соответствующие дереву и хордам графа, позволяет
однозначно определить матрицу N для системы
базисных контуров, отвечающих данному дереву.
Тем самым задача формирования уравнений
состояния электрической цепи произвольной
конфигурации сводится к составлению матрицы М,
разделению ее на блоки M
α
и M
β
выполнению над
ними стандартных операций.
Контурные
уравнения
Используя разделение матрицы М на две,
соответствующие дереву и хордам, запишем 1 з-н
Кирхгофа в виде
[]
J
I
I
MM =
⎥
⎦
⎤
⎢
⎣
⎡
×
β
α
βα
,
(5)
где I
α
, I
β
– столбцы токов в ветвях дерева и в хордах
Проведем операцию умножения M
α
×I
α
+ M
β
×I
β
=J
Выразим
ββ
−
α
−
αα
−= IMMJMI
11
(6)
Уравнение (**) представим в виде - N
αt
= M
β
M
α
-1
и
подставим в (6), получим
βα
−
αα
+= INJMI
t
1
(7)
Полный столбец искомых токов
β
α
−
α
β
βα
−
α
β
α
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
=
⎥
⎦
⎤
⎢
⎣
⎡
= I
1
N
J
0
M
I
INJM
I
I
I
t
t
1
1
,
используя разложение
[
]
βα
=
NNN и выбор
базисных контуров
1
=
β
N , получим N=[N
α
1],
транспонируем, тогда
β
−
α
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
= INJ
0
M
I
t
1
(8)
Подставим (8) во 2-й з-н Кирхгофа NZ
В
I=E
К
К
1
В
ЕINJ
0
M
NZ
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
β
−
α
t
Как понятно, токи в хордах являются контурными,
выразим слагаемое с I
β
(= I
К
)
J
0
M
NZЕINNZ
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−=
−
α
β
1
ВКВ t
или J
0
M
NZЕIZ
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−=
−
α
1
ВККК
, (***) где
Z
К
=NZ
В
N
t
– матрица контурных сопротивлений (ее
свойства потом) (квадратная неособенная матрица.
Решив уравнения контурных токов (***), определим
токи в контурах, затем в ветвях, затем падения
напряжения в ветвях и напряжения узлов
относительно балансирующего узла.
В результате задача определения параметров УР
решена.
Правила
определения
элементов
матрицы
контурных
сопротивлений
В силу диагональности матрицы сопротивлений
ветвей Z
В
произвольный элемент матрицы Z
К
определяется след. образом
∑
=
=
m
k
kkjkiij
ZnnZ
1
Поскольку каждый столбец матрицы N
соответствует ветви, а строка – контуру, можно
сформулировать правила определения элементов
матрицы Z
К
через сопротивления ветвей Z
В
1) недиагональный элемент Z
ij
равен алгебраической
сумме сопротивлений ветвей, одновременно
входящих в контуры i и j. Слагаемое будет
положительным, если направления обхода контуров
по данной ветви совпадают, и отрицательным, если
не совпадают. Если контуры не имеют общих ветвей
Z
ij
=0
2) диагональный элемент Z
ii
равен сумме
сопротивлений ветвей, образующих i-й контур
Свойства
матрицы Zк
1) диагональные элементы отличны от нуля и по
абсолютной величине превосходят недиагональные
элементы соотв. строки и столбца (см. как
образуются);
2) количество отличных от нуля недиагональных
элементов = k+2p, где k-число независимых
контуров, p- число пар контуров, имеющих общие
ветви;
3) матрица Zк симметричная , т. е. Z
ij
=
ji
.
Узловые
уравнения
Ранее мы получили (2): U
В
=M
t
U
∇
Подставим закон Ома для ветви в матричной форме
U
В
= Z
В
I-E в это уравнение, получим
M
t
U
∇
=Z
В
I-E
Решим его относительно I
()
EUMZI +=
∇
−
t
1
В
Подставим полученное выражение в 1-й з-н
Кирхгофа J=MI
EMZUMMZJ
1
В
1
В
−
∇
−
+=
t
или
EMZJUMMZ
1
В
1
В
−
∇
−
−=
t
обозначим
t
MMZY
1
ВУ
−
= – матрица узловых
проводимостей. Тогда окончательно
EMZJUY
1
ВУ
−
∇
−=
(4*) –система узловых
уравнений
Обычно эдс в ветвях отсутствуют, тогда
JUY
=
∇У
Формирование узловых уравнений сводится к
формированию матрицы узловых проводимостей
Правила
формирования
элементов
матрицы узловых
проводимостей
Матрица узловых проводимостей
t
MMYY
В
У
= (9) является квадратной,
поскольку матрица проводимостей ветвей, обратная
матрице сопротивлений ветвей – диагональная
Элемент матрицы определяется
∑
=
=
m
k
kjkikij
YmmY
1
(10)
Вспомним, что каждый столбец матрицы М
соответствует ветви, каждая строка – узлу. В каждом
столбце два ненулевых элемента –1 и +1, поэтому в
сумме только одна пара даст ненулевое
произведение
jkik
mm
и оно равно –1. Поэтому
1) любой недиагональный элемент матрицы
ij
Y
проводимостей равен взятой с обратным знаком
проводимости ветви между узлами i и j.
lij
YY
−
=
(11)
Если узлы не соединены, элемент матрицы =0
2) диагональные элементы матрицы из (10)
∑
=
=
m
k
kikii
YmY
1
2
,
т.е.
1
2
=
ik
m , если узел i является начальной или
конечной вершиной ветви k, и 0
2
=
ik
m , если ветвь k
не связана с узлом i. Следовательно, диагональный
элемент матрицы определяется суммой
проводимостей ветвей, связанных с узлом.
Свойства
матрицы узловых
проводимостей
(полной, т.е. с
балансир. узлом)
1) каждый из n диагональных элементов матрицы
равен сумме недиагональных элементов
соответствующей строки (или столбца), взятой с
обратным знаком, отсюда следует, что определитель
матрицы равен нулю, т. е. она является особенной;
2) в схемах замещения реальных систем
диагональные элементы матрицы
Y
∑
y
отличны
от нуля и, как правило, по абсолютной величине
превосходят недиагональные элементы
соответствующей строки или столбца;
3) количество отличных от нуля недиагональных
элементов равно удвоенному числу ветвей схемы
(2m), поэтому для матрицы порядка n, число
элементов которой равно
n
2
, количеств ненулевых
элементов равно
n+2m. Анализ схем замещения
современных сложных электрических систем
показывает, что число их ветвей примерно в 1,5 раза
больше числа узлов. Если принять
m=1,5n, то
количество ненулевых элементов в матрице
Y
∑
y
составит nnn 45,12
=
⋅
+
, а отношение
числа ненулевых элементов к общему числу
элементов равно
nnn
/
4
/
4
2
=
и снижается с
ростом
n. Таким образом, матрица
Y
∑
y
характеризуется слабой заполненностью, т.
е. большим числом нулевых элементов;
4) матрица
Y
∑
y
симметрична, поскольку
согласно (1-34)
,
YYY
ljiij
−
=
=
где l—номер
ветви, соединяющей узлы
i и j.
В результате задача определения параметров УР
решена
Правила
определения
элементов
матрицы
контурных
сопротивлений
В силу диагональности матрицы сопротивлений
ветвей
Z
В
произвольный элемент матрицы Z
К
определяется след. образом
∑
=
=
m
k
kkjkiij
ZnnZ
1
Поскольку каждый столбец матрицы N
соответствует ветви, а строка – контуру, можно
сформулировать правила определения элементов
матрицы
Z
К
через сопротивления ветвей Z
В
1) недиагональный элемент
Z
ij
равен алгебраической
сумме сопротивлений ветвей, одновременно
входящих в контуры
i и j. Слагаемое будет
положительным, если направления обхода контуров
по данной ветви совпадают, и отрицательным, если
не совпадают. Если контуры не имеют общих ветвей
Z
ij
=0
2) диагональный элемент
Z
ii
равен сумме
сопротивлений ветвей, образующих
i-й контур
Свойства
матрицы Zк
1) диагональные элементы отличны от нуля и по
абсолютной величине превосходят недиагональные
элементы соотв. строки и столбца (см. как
образуются);
2) количество отличных от нуля недиагональных
элементов = k+2p, где k-число независимых
контуров, p- число пар контуров, имеющих общие
ветви;
3) матрица Zк симметричная , т. е.
Z
ij
=
ji
.
Узловые
уравнения
Ранее мы получили (2):
∇
=
UMU
tв
Подставим закон Ома для ветви в матричной форме
EIZU −
=
вв
в это уравнение, получим
EIZUM −=
∇ вt
Решим его относительно
I
()
EUMZI +=
∇
−
t
1
В
Подставим полученное выражение в 1-й з-н
Кирхгофа
J=MI
EMZUMMZJ
1
В
1
В
−
∇
−
+=
t
или
EMZJUMMZ
1
В
1
В
−
∇
−
−=
t
обозначим
t
MMZY
1
ВУ
−
= – матрица узловых
проводимостей. Тогда окончательно
EMZJUY
1
ВУ
−
∇
−= (4*) –система узловых
уравнений
Обычно эдс в ветвях отсутствуют, тогда
JUY
=
∇У
(5*)
Формирование узловых уравнений сводится к
формированию матрицы узловых проводимостей
Правила
формирования
элементов
матрицы узловых
проводимостей
Матрица узловых проводимостей
t
MMYY
В
У
=
(9) является квадратной,
поскольку матрица проводимостей ветвей, обратная
матрице сопротивлений ветвей – диагональная
Элемент матрицы определяется
∑
=
=
m
k
kjkikij
YmmY
1
(10) (суммирование до m –
число ветвей)
Вспомним, что каждый столбец матрицы М
соответствует ветви, каждая строка – узлу. В каждом
столбце два ненулевых элемента –1 и +1, поэтому в
сумме только одна пара даст ненулевое
произведение
jkik
mm и оно равно –1. Поэтому
1) любой недиагональный элемент матрицы
ij
Y
проводимостей равен взятой с обратным знаком
проводимости ветви между узлами
i и j.
lij
YY −=
(11)
Если узлы не соединены, элемент матрицы =0
2) диагональные элементы матрицы из (10)
∑
=
=
m
k
kikii
YmY
1
2
, (12)
т.е.
1
2
=
ik
m , если узел i является начальной или
конечной вершиной ветви
k, и 0
2
=
ik
m , если ветвь k
не связана с узлом
i. Следовательно, диагональный
элемент матрицы определяется суммой
проводимостей ветвей, связанных с узлом.
Свойства
матрицы узловых
проводимостей
(полной, т.е. с
балансир. узлом)
Коэфф. заполнен.
1) каждый из
n диагональных элементов матрицы
равен сумме недиагональных элементов
соответствующей строки (или столбца), взятой с
обратным знаком, отсюда следует, что определитель
матрицы равен нулю, т. е. она является особенной;
2) в схемах замещения реальных систем
диагональные элементы матрицы
∑у
Y отличны от
нуля и, как правило, по абсолютной величине
превосходят недиагональные элементы
соответствующей строки или столбца;
3) количество отличных от нуля недиагональных
элементов равно удвоенному числу ветвей схемы
(2
m), поэтому для матрицы порядка n, число
элементов которой равно
2
n , количество ненулевых
элементов равно
n+2m.
Коэффициент заполненности матрицы
2
з
2
n
nm
k
+
=
Анализ схем замещения современных сложных
электрических систем показывает, что число их
ветвей примерно в 1,5 раза больше числа узлов. Если
принять
m=1,5n, то количество ненулевых элементов
в матрице
∑у
Y
составит nnn 45,12
=
⋅
+
, а
n
n
n
k
44
2
з
== снижается
с ростом
n. Таким образом, матрица
∑у
Y
характеризуется слабой заполненностью, т. е.
большим числом нулевых элементов;
4) матрица
∑у
Y симметрична, поскольку
ljiij
YYY
−
=
=
, где l—номер ветви, соединяющей
узлы
i и j.
Почему дальше
изучаем метод
узл. напряжений
По практике расчетов в обобщенной форме – много
уравнений, сложнее,
контурные уравнения – их
количество k=m-n+1,
узловых напряжений k=n-1.
Методом
контурных уравнений их кол-во меньше,
но зато формирование их более сложно для цепей с
большим кол-вом элементов. Поэтому в расчетах
электрических сетей в УР чаще всего используются
узловые уравнения или
метод узловых напряжений.
Поэтому рассмотрим подробно именно этот метод.
(МКТ - аналогичен, техника решений та же)
Постановка
задачи
Мы получили уравнение (5*)
JUY
=
∇У
В этом уравнении используются фазные значения
напряжений и токов. В расчетах УР эл. сетей обычно
используют линейные напряжения и токи, тогда
наше уравнение примет вид
JUY 3
У
=
∇
(6*)
Чтобы получить эту систему уравнений для
конкретной схемы, нам должно быть дано
:
1)
значения всех проводимостей ветвей, или
сопротивлений;
2)
токи всех источников тока и токи нагрузки
потребителей во свех узлах, кроме
балансирующего
3)
напряжение балансирующего узла
Напоминание: для удобства вычислительных
процедур базисный по напряжению и и
балансирующий по мощности берется один и тот же
узел
Определить
: напряжения в узлах и токи в ветвях
Случай 0
б
=U
Если в схеме замещения присутствуют поперечные
ветви, т.е. есть связи с нейтралью, то в качестве
балансирующего удобно взять нейтраль. Тогда
уравнение (6*) примет вид
JUY 3
У
= (13)
Напоминание: смысл величин, как считаются
(формула 11) (12)
Поскольку сначала считаются проводимости между
узлами по (11), то для (12) удобнее представить
∑∑
+
≠
==
−==
1
11
n
kj
j
kj
m
k
lkii
YYY (14)
Определение вектора задающих токов: для каждого
узла задающий ток равен алг. сумме токов
источников (нагрузки), подключенных к узлу. Токи
потребления и генерации, естественно, должны
иметь разные знаки.
узел генерир. | нагрузочный
Сост.: | акт. | реакт. | акт. | реактивная |
+ – – инд.+| емк.–
В (13) величины комплексные, разделим мнимые и
действ. части
⎪
⎩
⎪
⎨
⎧
+=
+=
−=
J"J'J
U"U'U
BGY
j
j
j
ууу
(15)
Подставим в (13)
(
)
()
(
)
I"I'U"U'BG jjj +=+⋅− 3
уу
Распишем отдельно дейтсв. и мнимые части
⎪
⎩
⎪
⎨
⎧
=+−
=+
I"U"GU'B
I'U"BU'G
3
;3
уу
уу
или в матричном виде
I"
I'
U"
U'
GB
BG
3
=⋅
−
уу
уу
(16)
Случай 0
б
≠
U
Если схема не содержит поперечных ветвей, то в
качестве балансирующего берут один из
генераторных узлов (обычно соответствующий
мощной электростанции, ведущей по частоте),
напряжение которого задано
U
б
.
Уравнение (6*) может быть представлено в виде
ббУ
3 UYJUY −= (17)
Аналогично тому, как мы разделили действ. и
мнимые части для случая нулевого напряжения в
балансирующем узле, проведя же преобразования,
получим
бб
бб
уу
уу
U
U
b
g
I"
I'
U"
U'
GB
BG
−
−=⋅
−
3 (18)
Получили систему 2
n уравнений. СЛАУ! Далее –
решить.
Методы решения СЛАУ
Классификац
ия методов
– точные (Гаусса, схема Жордана)
– итерационные (простой итерации, Зейделя)
Общее описание методов
Метод
Гаусса=метод
последовател
ьного
исключения
Самый распространенный метод, есть несколько
реализующих метод алгоритмов. Самый
распространенный алгоритм единственного деления (или
алгоритм с обратным ходом)
Имеем систему уравнений (16) или (18), т.е. если
расписать, имеем (19)
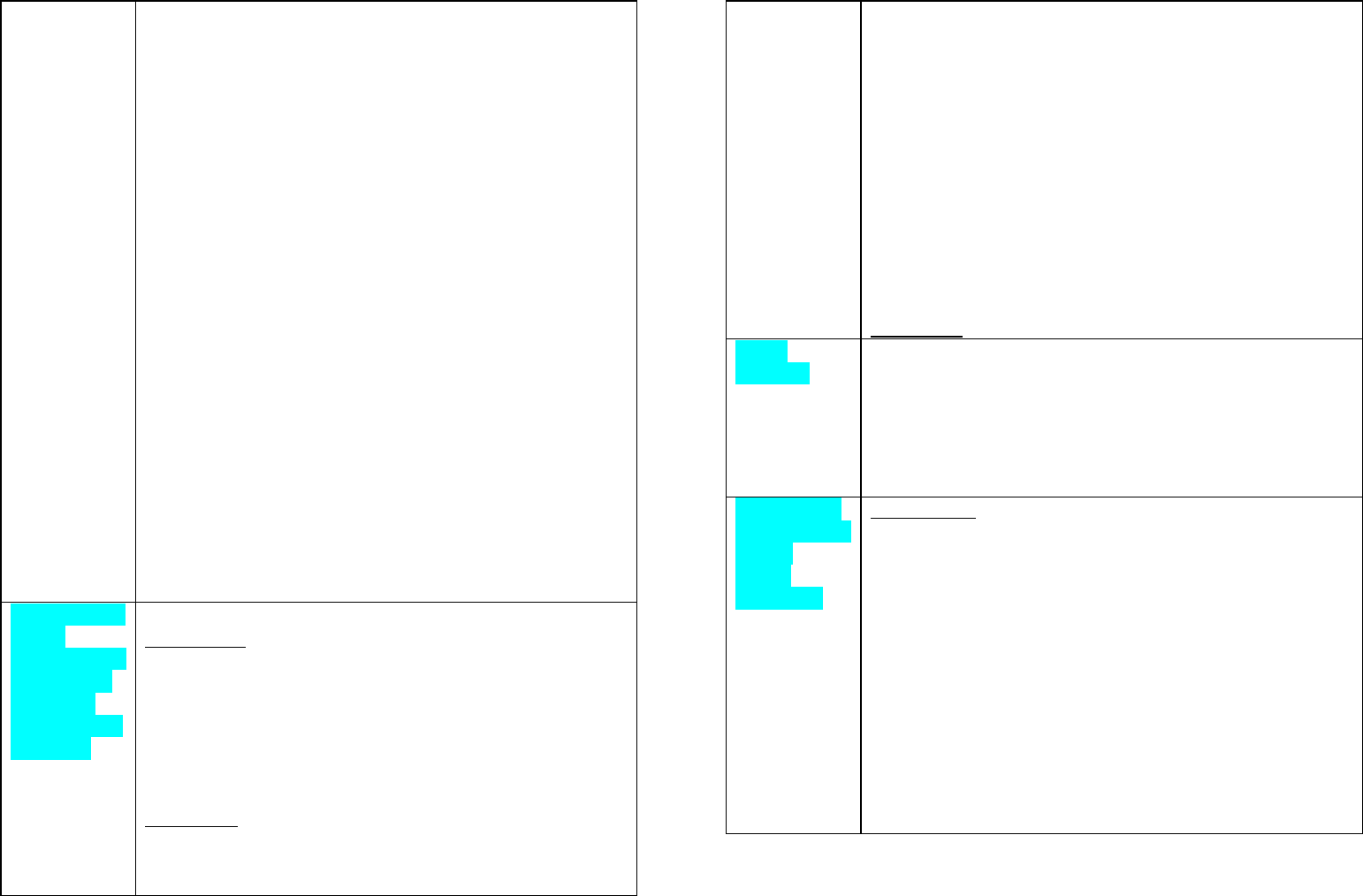
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=++++−−−−
=++++−−−−
=+++++++
=+++++++
=+++++++
n
nnnnnnnnnn
nnnn
nnnnnnnnnnn
nnnn
nnnn
JUgUgUgUbUbUb
JUgUgUgUbUbUb
JUbUbUbUgUgUg
JUbUbUbUgUgUg
JUbUbUbUgUgUg
"'...""'...''
....
"'...""'...''
'"...""'...''
.....
'"...""'...
''
'"...""'...''
"22112211
1"12121111212111
212112211
222221212222121
112121111212111
Формализовать задачу, т.е. коэффициенты и неизвестные
записать в общем виде
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
nnnnnn
nn
nn
cUaUaUa
cUaUaUa
cUaUaUa
...
....
...
...
2211
22222121
11212111
(20)
Глобально алгоритм разделяется на 2 этапа: прямой ход и
обратный. Задача прямого хода – свести систему
уравнений к треугольной типа
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=++
=+++
nnnn
nn
nn
bUb
bUbUb
bUbUbU
....
...
...
22222
112121
(21)
Обратный ход – нахождение решения подстановкой
решений снизу
Общее количество действий
3
n≈ – много!
Последовател
ьность
действий при
выполнении
алгоритма
единственног
о деления
Прямой ход
Действие 1.
преобразовать матрицу n×n таким образом,
чтобы диагональные элементы были доминирующими,
т.е. по абсолютной величине наибольшими в строке. При
этом столбик переменных перемещается полностью
Пример: -2u
1
+3u
2
-6u
3
+u
4
=-6 -6u
3
-2u
1
+3u
2
+u
4
=-6
5u
1
- u
2
+3u
3
=5 3u
3
+5u
1
–u
2
=5
u
1
+7u
2
-2u
4
=1 u
1
+7u
2
-2u
4
=1
-u
1
-2u
2
+3u
3
-4u
4
=-8 3u
3
-u
1
-2u
2
-4u
4
=-8
Действие 2. Прямой ход.
Шаг 1. Исключаем из всех уравнений, начиная со
второго, первый член, для чего
а) разделить все коэффициенты и свободный член на
коэффициент при первом уравнении (на –6);
б) получившееся в результате шага 1а уравнение
умножить на коэффициент перед первым членом
i-того
уравнения с обратным знаком и сложить эти два
уравнения. В результате действий первый член в
i-том
уравнении обратится в 0. (2: 1а
×-3, сложить 1а и рез-т)
Шаг 2. Исключить из всех уравнений, начиная с 3-го 2-й
член, для чего
а) уравнение 1а переписать без изменений
б) для укороченной на 1-й член системы проделать
операции шага 1
Шаг 3 и далее. Повторять операции шага 2, пока не
придем к треугольной системе уравнений.
Действие 3
. Обратный ход.
Схема
Жордана
=алгоритм без обратного хода:
действие1, шаг 1 те же. Начиная с шага 2 проводятся
дополнительные операции с уравнениями от1 до
i-1, в
которых проводятся преобразования таким образом,
чтобы коэффициент столбца, соответствующий
преобразуемому уравнению обратился в 0. Операций еще
больше, поэтому редко применяется.
Достоинства
и недостатки
метода
Гаусса
(Жордана)
Достоинства
: простота, наглядность
Недостатки: возможна большая погрешность, вызванная
1) округлением результатов расчетов (диагональный
элемент близок к нулю – избегаем, но на следующих
шагах возможно)
2) неточностью задания исходных данных. Всегда
присутствует погрешность в задании параметров
системы. Как правило, погрешность полученных
решений бывает соизмерима с погрешностью задания
параметров системы, т.е. коэффициентов матрицы.
Однако
могут быть случаи, когда погрешность исх.
данных дает очень большую погрешность решения.
Причина –
плохая обусловленность матрицы
коэффициентов, признаком кторой является малость
определителя матрицы относительно оценки Адамара
