Медведева С.Н. Курс лекций Математические задачи в энергетике
Подождите немного. Документ загружается.


⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−−=
∑∑
+=
−
=
++
бб
)(*
*
1
)(
1
1
)1()1(
1
UY
U
S
UYUY
Y
U
k
i
k
k
n
kj
i
j
kj
k
j
i
j
kj
kk
i
k
– метод Зейделя.
Сходимость итерационных методов к решению медленная. Для
ускорения применяют метод ускоряющих коэффициентов = метод неполной
релаксации.
Достоинства итерационных процессов – простота.
Недостаток – медленная сходимость, м.б. расходимость. Особенно
медленно процесс сходится при расчете схем с устройствами продольной
компенсации, с трехобмоточным трансформатором или автотрансформатором
с очень малым сопротивлением обмотки среднего напряжения, а также для
систем с сильной неоднородностью параметров.
Особенности сходимости СНАУ:
1) сходимость зависит от выбора начальных приближений, может
сойтись, может и
не сойтись (для СЛАУ всегда сходится, разное число
итераций);
2) область существования решения ограничена, оно существует на
некотором ограниченном диапазоне изменения вектора S
у
.

ЛЕКЦ. 2-4: ФОРМЫ ЗАПИСИ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ
РЕЖИМА ДЛЯ ОБЩЕГО СЛУЧАЯ ЗАДАНИЯ ИСХОДНЫХ ДАННЫХ
Особенности записи узловых уравнений УР для реальных задач
В системе уравнений формы (3) источники (генераторы) и потребители
(нагрузка) заданы полными мощностями или активной и реактивной
мощностью (их постоянным значением).
В реальных задачах генераторы, как правило, задаются значением
активной мощности
const
г
=
P и активной составляющей напряжения
const
г
=U . Таким же образом задаются синхронные компенсаторы и
регулируемые статические источники реактивной мощности (о них далее 4-5
курс). Потребители задаются статическими характеристиками активной и
реактивной мощности по напряжению (СХН) (более подробно о них в курсе
«Электроэнергетические системы и сети»).
По потребителям: указанное более общее задание нагрузок не меняет
вида уравнения (3), требуется лишь
дополнительная коррекция мощностей по
напряжению. Процедура коррекции будет сказываться на сходимости
итерационного процесса. Собственно алгоритм принципиально не меняется.
Принципиально другой случай с источниками (генераторами): задание
const
г
=P и const
г
=U изменяет состав заданных и искомых параметров
уравнения (3).
Определим состав параметров уравнений установившегося режима в
(3): каждый k-й узел схемы замещения электрической системы
характеризуется двумя комплексными или четырьмя вещественными
параметрами режима:
k
S и
k
U – для комплексных или
k
P ,
k
Q ;
k
U ,
k
δ
– для вещественных. Для
пассивных узлов
0
=
i
P , 0
=
i
Q (пассивный узел – нет ни генераторов, ни
нагрузки).
Количество уравнений для каждого узла: одно комплексное или два
вещественных баланса мощности. Следовательно, для каждого узла два
вещественных параметра должны быть заданы, два ищем.
Для генераторных узлов
даны
k
P ,
k
U , → найти
k
Q ,
k
δ
.
Для нагрузочных узлов
даны
k
P ,
k
Q → найти
k
U ,
k
δ
.
Введение в схему замещения узлов с заданными
k
P и
k
U усложняет
вычислительную процедуру итерационных методов.
Покажем это на примере метода Зейделя, для которого алгоритм
расчетов изменится следующим образом:
1) для каждого k-того узла вычисляется не
)1( +i
k
U , а
)1( +i
k
V –
составляющая
)1( +i
k
U , не зависящая от
k
Q (т.е
)1( +i
k
V определяется как
)1( +i
k
U при
k
Q =0)
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+−
∑
−
∑
−=
+=
−
=
++
)(
б
б
1
)(
1
1
)1()1(
ˆ
1
i
k
k
k
n
kj
i
j
jk
k
j
i
j
jk
kk
i
k
U
P
UYUYUY
Y
V
, (3.1)
2) считаем
)(
)1(
)1()1(
ˆ
i
k
kk
i
k
i
k
i
k
UY
Q
jVU
+
++
−= , (3.2)
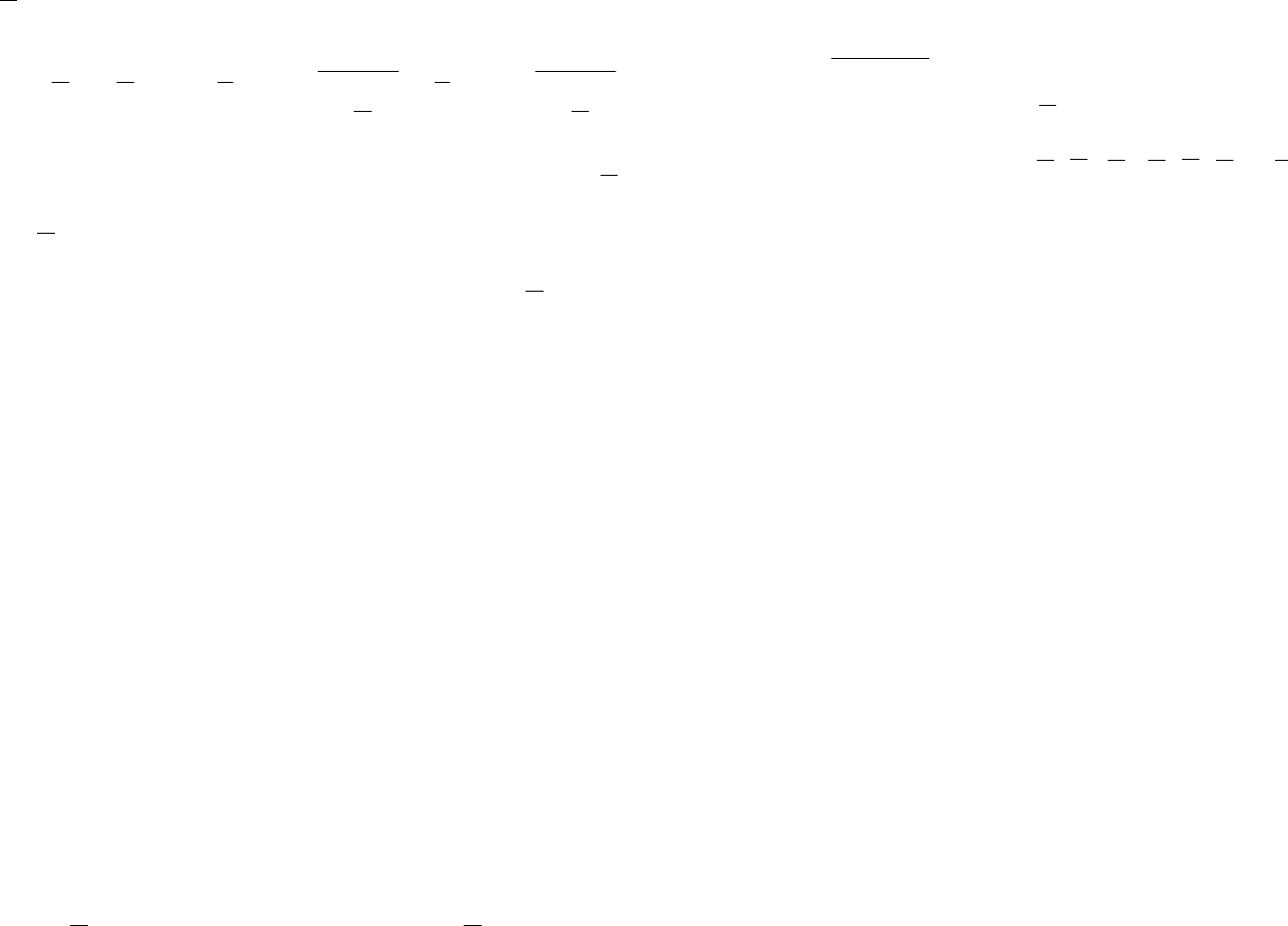
тогда
)1( +i
k
Q найдем, решив квадратное уравнение
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+⋅
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−==
+
+
+
+
+
+
)(
)1(
)1(
)(
)1(
)1(
)1(
)1(
2
ˆˆ
ˆ
i
k
kk
i
k
i
k
i
k
kk
i
k
i
k
i
k
i
kk
UY
Q
jV
UY
Q
jVUUU
. (3.3)
Для решения (3.3) учитываем, что здесь одно неизвестное
)1( +i
k
Q , а
величина
const
)1(
==
+
k
i
k
UU задана.
3) решив (3.3), подставляем в (3.2), находим
)1( +i
k
U и далее
итерационный процесс.
Метод простой итерации аналогичен методу Зейделя, чуть проще.
Применение метода Гаусса влечет значительное усложнение, поскольку
задание в качестве известных параметров
k
P и
k
U не позволяет свести
систему уравнений к виду (3), т.е. к нелинейной системе алгебраических
уравнений, линейной слева. Это приводит не только к усложнению
вычислительной процедуры, но и к заметному ухудшению сходимости
итерационного процесса.
Для повышения вычислительной эффективности решения СНАУ
установившегося режима в общем случае задания исходных данных могут
быть использованы методы,
применение которых требует дифференцирования
уравнений по искомым параметрам, например, метод Ньютона, градиентные и
др.
При этом необходим переход от комплексных уравнений к
вещественным, поскольку в уравнении (3) имеются как комплексы искомых
параметров
U
, так и сопряженные комплексы U
ˆ
, а в этом случае
производные можно брать только отдельно по вещественным переменным.
Рассмотрим возможные формы записи нелинейных узловых уравнений
установившегося режима (УР).
во-первых
, можно записать в форме баланса токов (выражение 3) или
мощностей [выражение (3)
д
ˆ
U× ]
уб
бУ
SUYUUYU
ˆ
ˆˆ
дд
=+ . (3в)
во-вторых, переход от комплексных к вещественным параметрам
можно осуществить на основе записи комплексных чисел либо в
прямоугольной, либо в полярной системе координат (СК).
Отсюда следуют 4 формы записи СНАУ вида (3=3а).

ЛЕКЦ. 2-5: ФОРМЫ ЗАПИСИ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ
РЕЖИМА ДЛЯ ОБЩЕГО СЛУЧАЯ ЗАДАНИЯ ИСХОДНЫХ ДАННЫХ
(ПРОДОЛЖЕНИЕ ТЕМЫ)
Рассмотрим 4 формы записи СНАУ вида (3=3а), которую запишем еще
раз
б
б
у
1
д
у
UYSUUY −=
−
)
)
. (3)
1. Узловые уравнения УР в форме баланса токов в прямоугольной
системе координат
Распишем комплексные выражения через их действительные и мнимые
составляющие:
,
,
;"'
;
бб
б
у
BGY
BGY
UUU
QPS
j
j
j
j
−=
−=
+=
+=
(4.1)
где P и Q – вектор-столбцы соответственно активной и реактивной
составляющих мощностей в узлах; U’ и U” – вектор-столбцы действительных
и мнимых составляющих вектор-столбца искомых напряжений в узлах
системы; G и B – квадратные матрицы порядка N.
Знак “-“ в выражениях для проводимостей введен для удобства записи,
поскольку
()()
jbg
xr
x
j
xr
r
jxrjxr
jxr
jxr
Y −=
+
−
+
=
−⋅+
−
=
+
=
2222
1
.
Подставив эти выражения в (3), с учетом общепринятого
бб
U
=
U ,
получим
()( )
(
)
()( )
ббб
1
дд
"'"' Ujjjjj ⋅−−−⋅−=+⋅−
−
BGQPUUUUBG .
Раскрываем скобки
(
)
(
)
()()
=+−
−⋅+
−
⋅
+
=++−
бббб
дддд
дд
"'"'
"'
""'' UjU
jj
jj
jj BG
UUUU
QPUU
BUGUBUGU
(учтем, что знаменатель равен разности квадратов, а следовательно
(
)( )
2
д
2
д
2
д
"' UUU =+
– в знаменателе диагональная матрица квадратов
напряжений)
бббб
2
дд
2
дд
2
дд
2
дд
""'' UjUjj BGQUUPUUQUUPUU +−++−=
−−−−
.
Разделим действительные и мнимые части уравнения на два векторных
уравнения отдельно для действительной и мнимой части
⎪
⎭
⎪
⎬
⎫
++−=+−
−+=+
−−
−−
,"'"
;"'
бб
2
дд
2
дд
бб
2
дд
2
дд
Uj
U
BPUUQUUGUBU'
GQUUPUUBU"GU'
(4.2)
где
{
}
22
д
diag
−−
=
k
UU .
В развернутом виде система уравнений принимает вид (для k–го узла):
⎪
⎪
⎭
⎪
⎪
⎬
⎫
++−=
∑
+
∑
−
−+=
∑
+
∑
==
==
.
"'
"'
;
"'
"'
бб
22
11
бб
22
11
UbP
U
U
Q
U
U
UgUb
UgQ
U
U
P
U
U
UbUg
kk
k
k
k
k
k
N
j
jkj
N
j
jkj
kk
k
k
k
k
k
N
j
jkj
N
j
jkj
(4.2а)
2. Узловые уравнения УР в форме баланса токов в полярной системе
координат
Для получения этих уравнений удобно воспользоваться развернутой
(не матричной!) формой записи исходной системы уравнений (3), то есть
б
б
1
ˆ
UY
U
jQP
UY
k
k
kk
N
j
j
kj
−
−
=
∑
=
. (4.3)
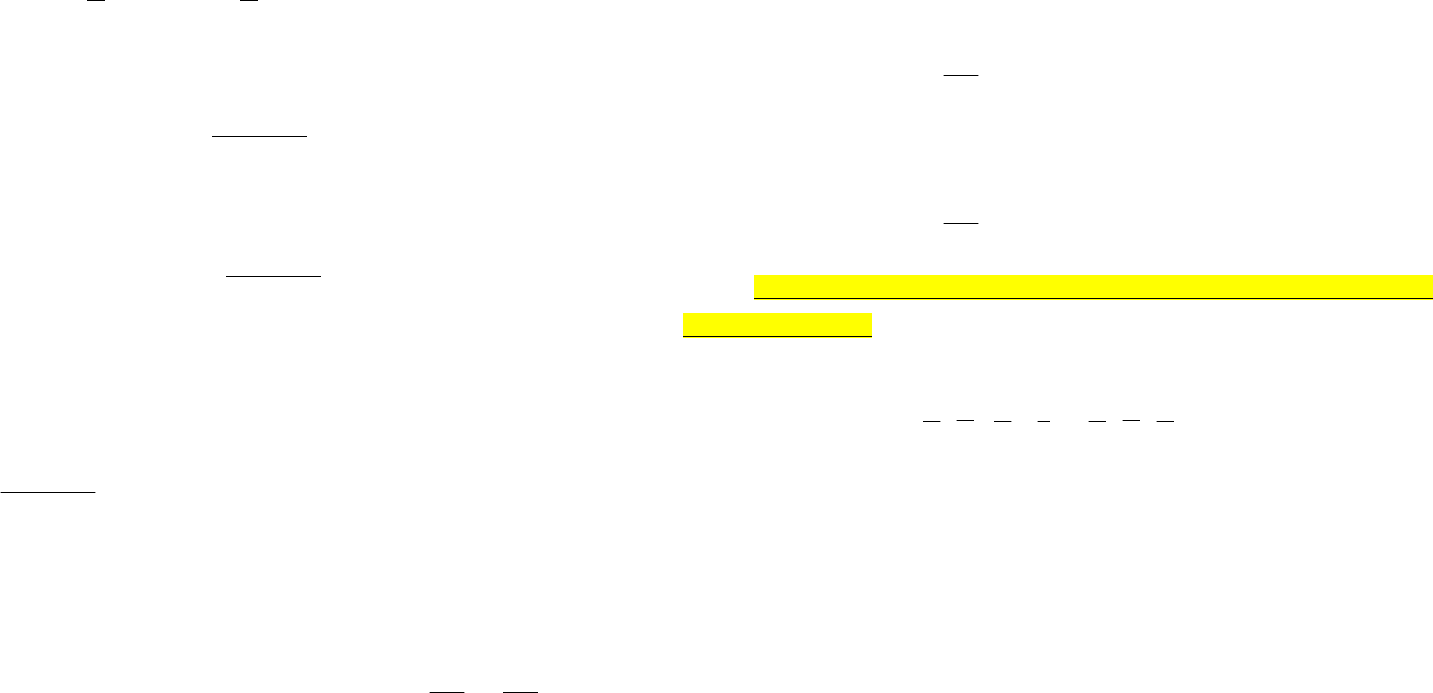
В полярной СК
j
j
j
j
eUU
δ
= ,
k
j
k
k
eUU
δ
=
.
Подставим эти выражение в (4.3) и разделим комплексное выражение
проводимости на действительную и мнимую части:
()
()
ббб
1
Ujbge
U
jQP
eUjbg
kk
j
k
kk
j
N
j
jkjkj
k
j
−−⋅
−
=⋅
∑
⋅−
δ
δ
=
.
Разделим обе части уравнения на
k
j
e
δ
.
()
(
)
()
k
kj
j
kk
k
kk
j
N
j
jkjkj
eUjbg
U
jQP
eUjbg
δ−
δ−δ
=
⋅−−
−
=⋅
∑
⋅−
ббб
1
.
Учтем, что по формуле Эйлера
α+α=
α
sincos je
j
, тогда
()()
(
)
[]
()( )
;sincos
sincos
ббб
1
kkkk
k
kk
kjkj
N
j
jkjkj
jUjbg
U
jQP
jUjbg
δ−δ⋅⋅−−
−
=
=δ−δ+δ−δ⋅
∑
⋅−
=
.
Раскрываем скобки
() ()
() ()
;sinsincoscos
sinsin
coscos
бббббббб
11
11
kkkkkkkk
k
k
k
k
N
j
kjjkj
N
j
kjjkj
N
j
N
j
kjjkjkjjkj
UbUjgUjbUg
U
Q
j
U
P
UbUgj
UbjUg
δ+δ+δ+δ−
−−=
∑
δ−δ+
∑
δ−δ+
+
∑∑
δ−δ−δ−δ
==
==
Сменим фазу, поскольку логичнее определять фазу относительно узла,
для которого пишем уравнение, т.е.
)cos(cos
α
−
=α , )sin(sin
α
−
−
=
α
, и
разделим действительную и мнимую части. Для мнимой части еще сменим
знак. В результате получаем:
() ()
[]
()
() ()
[]
()
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
δ+δ−=
=⋅
∑
δ−δ+δ−δ
δ−δ−=
=⋅
∑
δ−δ−δ−δ
=
=
kkkk
k
k
j
N
j
jkkjjkkj
kkkk
k
k
j
N
j
jkkjjkkj
bgU
U
Q
Ubg
bgU
U
P
Ubg
cossin
cossin
;sincos
sincos
ббб
1
ббб
1
(4.4)
3. Узловые уравнения УР в форме баланса мощностей в прямоугольной
системе координат
Для вывода используем уравнение в виде (3в)
б
бУ
UYUSUYU
дуд
ˆ
ˆ
ˆ
−=
.
Подставляем в него соотношения (4.1)
(
)
(
)
(
)
(
)
(
)
бббдддд
"'"'"' Ujjjjjj ⋅−
⋅
−
−
−
=
+
⋅
−
⋅
− BGUUQPUUBGUU .
Раскрываем вторые и третьи скобки слева и скобки справа
(
)
(
)
()
ббдбдбдбд
дд
""''
""''"'
Ujjj
jjj
⋅−−−−−
=
+
+
−
⋅
−
BUGUBUGUQP
BUGUBUGUUU
.
Разделяем вещественную и мнимую части
()
(
)
(
)
()()
()
⎭
⎬
⎫
⋅+−=+⋅+−⋅
⋅−−=−⋅−+⋅
."'"'""''
;"'"'""''
ббдбддд
ббдбддд
U
U
GUBUQBUGUUGUBUU
BUGUPGUBUUBUGUU
(4.5)
В развернутом виде

()()
()
()()
()
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
+−=
=
∑
++
∑
−
−−=
=
∑
−−
∑
+
==
==
."'
"'""''
;"'
"'""''
ббб
11
ббб
11
UgUbUQ
UbUgUUgUbU
UbUgUP
UgUbUUbUgU
kkkkk
N
j
jkjjkjk
N
j
jkjjkjk
kkkkk
N
j
jkjjkjk
N
j
jkjjkjk
(4.5а)
4. Узловые уравнения УР в форме баланса мощностей в полярной
системе координат
Получим из (4.4), умножив каждое уравнение на модуль
соответствующего узла
() ()
[]
()
() ()
[]
()
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
δ+δ−=
=⋅
∑
δ−δ+δ−δ⋅
δ−δ−=
=⋅
∑
δ−δ−δ−δ⋅
=
=
kkkkkk
j
N
j
jkkjjkkjk
kkkkkk
j
N
j
jkkjjkkjk
bgUUQ
UbgU
bgUUP
UbgU
cossin
cossin
;sincos
sincos
ббб
1
ббб
1
(4.6)
ЛЕКЦ. 2-6: ФОРМЫ ЗАПИСИ УРАВНЕНИЙ УСТАНОВИВШЕГОСЯ
РЕЖИМА ДЛЯ ОБЩЕГО СЛУЧАЯ ЗАДАНИЯ ИСХОДНЫХ ДАННЫХ
(ПРОДОЛЖЕНИЕ ТЕМЫ)
Сделаем выводы по 4 формам записи СНАУ установившегося режима
электрической сети, каждая из которых имеет свои преимущества,
определяющие область ее рационального применения:
1) Узловые уравнения в форме баланса токов в прямоугольной СК
линейны слева (преимущество), следовательно, их можно решать с помощью
итерационных методов. То есть, если есть программа, реализующая
итерационный процесс, то предпочтительнее сформировать узловые уравнения
в форме баланса токов в прямоугольной СК.
2) Уравнения в форме баланса мощностей позволяют относительно
просто учитывать разное задание исходных данных для нагрузочных и
генераторных узлов (генераторный P
i
, U
i
, нагрузочный P
i
, Q
i
). То есть для
генераторного узла достаточно заменить уравнение баланса реактивной
мощности во втором уравнении формы 3 (выражения 4.5) на уравнения
()( )
2
22
"'
k
kk
UUU =+
.
3) Наиболее просто осуществляется такой учет в уравнениях формы 4,
т.е. в форме баланса мощностей в полярной СК. Для генераторных узлов в
этой системе уравнений надо просто исключить уравнения баланса
реактивных мощностей.
Общий недостаток для всех форм – уравнения трансцендентны, т.е.
содержат тригонометрические функции, что увеличивает объем и
трудоемкость вычислений при их решении.
Полученные уравнения содержат дифференцируемые функции,
следовательно, для решения можно применять градиентный метод и метод
Ньютона. Основной недостаток градиентных методов – медленная сходимость
итерационного процесса по мере приближения к решению, поэтому
градиентный
метод не нашел самостоятельного применения для решения
узловых уравнений установившегося режима. Зато метод Ньютона
применяется как стандартный, т.к. он характеризуется быстрой сходимостью.
Тема: Решение системы нелинейных уравнений методом Ньютона
Идея метода Ньютона
Метод Ньютона пригоден для решения обширного класса нелинейных
задач. Идея его заключается в последовательной линеаризации системы
нелинейных уравнений на каждом шаге итерации. Решение линеаризованной
системы дает значение неизвестных, которое ближе к решению, чем
предыдущее приближение.
Проиллюстрируем идею на примере одного нелинейного уравнения и в
графике. Нужно решить уравнение
0)(
=
xw . (1)
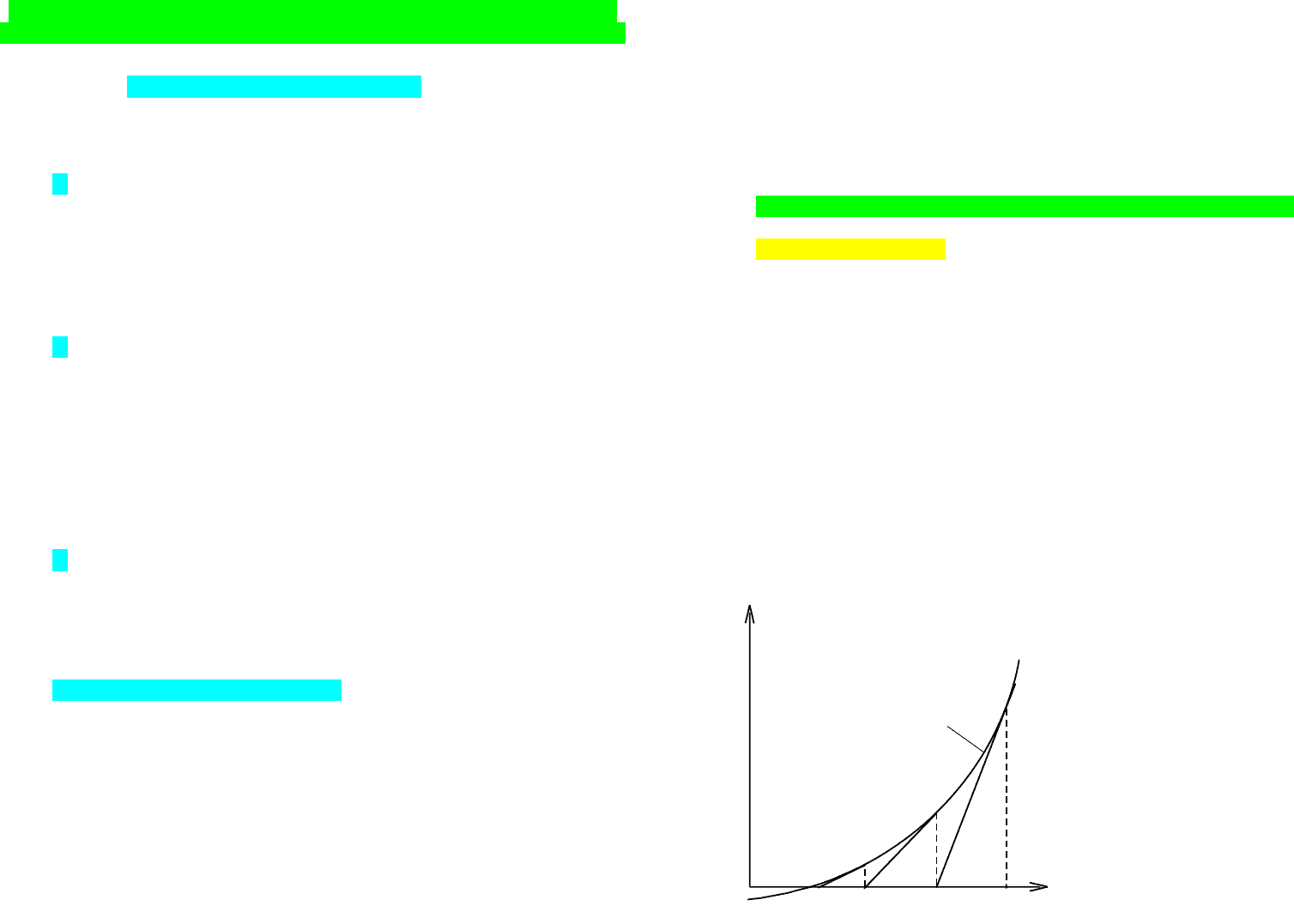
Графически его решение – это точка
x
~
, в которой кривая )(xw
проходит через 0 (см. рис.).
Зададим начальное
приближение х
<0>
Уравнение (1)
линеаризуем в окрестности
точки х
<0>
, то есть на графике
проводим касательную к точке
х
<0>
. Из рисунка видно
0
x
~
x
x
<2>
<1> <0>
x
w(x)
w(x)
x

><><
><
−
=α
10
0
tg
xx
w
или
α
=−
><
><><
tg
0
10
w
xx
.
В то же время по определению
(
)
x
xw
∂
∂
=α
><0
tg .
После несложных преобразований получим
(
)
()
x
xw
xw
xx
∂
∂
−=
><
><
><><
0
0
01
(2)
Обобщим выражение (2) для любого шага итерации:
(
)
()
x
xw
xw
xx
i
i
ii
∂
∂
−=
><
><
><>+< 1
(3)
Итерационный процесс сходится, если функция
)(xw становится
близкой к 0. Сходимость считается достигнутой, а итерационный процесс
законченным, если абсолютная величина невязки (небаланса) меньше
заданной.
Далее рассмотрим применение идеи для решения не обного уравнения,
а системы.
Решение СНАУ методом Ньютона.
Имеем систему нелинейных уравнений в общем виде
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
=
=
,0),..,,(
...
;0),..,,(
;0),..,,(
21
212
211
NN
N
N
xxxW
xxxW
xxxW
(5.1)
где W
i
– дифференцируемые функции переменных x
i
.
В матричном виде
0
=
W(X) , (5.2)
где W, X– вектор-функция и вектор переменных.
Аналогично алгоритму решения одного уравнения суть метода
Ньютона состоит в линеаризации системы уравнений в точке заданного
приближения
><i
X , затем полученная СЛАУ решается, получаем
>+< 1i
X .
Линеаризация производится путем разложения вектор-функции в ряд Тейлора
и отбрасывания членов разложения порядка выше первого. То есть
итерационная формула метода Ньютона имеет вид
0
)(
)(
)(
=Δ
∂
∂
+
i
i
i
X
X
)W(X
)W(X
, (5.3)
где
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
∂
∂
=
∂
∂
Nji
X
W
j
i
..1, ,
X
W
– квадратная матрица частных производных
или иначе матрица Якоби;
)()1()( iii
XXX
−
=
Δ
+
Выражение (5.3) представляет собой СЛАУ вида
)W(XX
X
)W(X
)()(
)(
ii
i
−=Δ
∂
∂
(5.4)
с неизвестными
)(i
X
Δ
.
Решение существует при условии, что матрица коэффициентов
(матрица Якоби) не особенная, т.е. определитель матрицы (якобиан) не равен
нулю.

Оценка условий сходимости итерационного процесса метода Ньютона.
Предположим, что решение (5.2) существует и равно Х*, т.е.
0≡W(X*)
. Разложим W(X) в ряд Тейлора в точке некоторого приближения
)()(
*
ii
εXX −= и W(X*) определим как
0
2
1
)()(
2
)(2
)(
)(
)(
=
∂
∂
+
∂
∂
+=
ii
i
i
i
i
εε
X
)W(X
ε
X
)W(X
)W(XW(X*)
, (5.5)
где
)(i
ε – некоторый вектор, компоненты которого зависят от Х* и
)(i
X ;
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
∂∂
∂
=
∂
∂
Nlji
XX
W
lj
i
..1,, ,
2
2
2
X
W
– кубическая матрица (N×N×N), матрица
вторых производных или матрица Гессе.
Согласно (5.3)
)W(X
X
)W(X
XX
)(
1
)(
)()1( i
i
ii
−
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
−=
. (5.6)
Из (5.5), поделив все члены уравнения на матрицу Якоби и выразив
первый член, запишем
)()(
2
)(2
1
)(
)()(
1
)(
2
1
ii
ii
ii
i
εε
X
)W(X
X
)W(X
ε)W(X
X
)W(X
∂
∂
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
+=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
−
−−
.
Подставим последнее выражение в (5.6)
)()(
2
)(2
1
)(
)()()1(
2
1
ii
ii
iii
εε
X
)W(X
X
)W(X
εXX
∂
∂
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
++=
−
+
или, если учесть
*
)()(
XεX =+
ii
)()(
2
)(2
1
)(
*)1(
2
1
ii
ii
i
εε
X
)W(X
X
)W(X
XX
∂
∂
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
+=
−
+
.
Следовательно, если погрешность i-того приближения равна
)(*)( ii
XXε −= , то после выполнения шага итерации по методу Ньютона
получим (i+1)-е приближение, погрешность которого
)()(
2
)(2
1
)(
*)1()1(
2
1
ii
ii
ii
εε
X
)W(X
X
)W(X
XXε
∂
∂
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
=−=
−
++
. (5.7)
Из (5.7) следует, что
1) условия сходимости метода Ньютона зависят
а) от значений первых и вторых производных функций невязок по
искомым параметрам;
б) от близости предыдущего, а в конечном итоге начального
приближения к решению. При этом погрешность последующего приближения
связана с погрешностью предыдущего решения квадратичной зависимостью. В
этом смысле говорят о квадратичной
сходимости метода Ньютона.
2) по мере приближения к решению сходимость резко ускоряется.
3) при задании начального приближения достаточно далеко от решения
итерационный процесс метода Ньютона может быть расходящимся.
Для устранения недостатка п.3 рассмотрим далее подходы для
обеспечения надежности сходимости итерационного процесса.
ЛЕКЦ. 2-7: РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
МЕТОДОМ НЬЮТОНА (ПРОДОЛЖЕНИЕ ТЕМЫ)
Подходы, обеспечивающие увеличение надежности сходимости
итерационного процесса метода Ньютона.
В теории оптимизации доказано положение: сумм квадратов
небалансов
Тема: Применение метода Ньютона для решения уравнений
установившегося режима электрической системы
Лекц. 2-8: Применение метода Ньютона для решения уравнений
установившегося режима электрической системы (продолжение темы)
В предыдущей лекции мы получили первое уравнение для
вычислительного алгоритма метода Ньютона в форме баланса токов в
прямоугольной СК. Этого достаточно для понимания методики вывода
расчетных формул. Поэтому далее мы просто запишем формулы для
итерационного процесса метода Ньютона в различных формах и отметим
особенности
каждой из форм.
Вычислительные алгоритмы метода Ньютона для различных форм
Узловые уравнения в форме баланса токов в прямоугольной СК
Вычислительная схема итерационного процесса
⎥
⎦
⎤
⎢
⎣
⎡
−=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
W"
W'
ΔU"
ΔU'
U"
W"
U'
W"
U"
W'
U'
W'
.
В матричной форме составляющие имеют вид (7.1,а)
;
22
д
3
ддд
д
3
д
2
д
д
4
дддд
4
д
2
дд
2
д
U
Q
UU'U"
U
P
UU'
QUU'U"PUU'PUG
U'
)U",(U'W'
∂
∂
−
∂
∂
−
−++−=
∂
∂
−−
−−−
;"
"22
д
3
д
2
д
д
3
ддд
д
4
д
2
дд
4
дддд
2
д
U
Q
UU
U
P
UU"U'
QUUPUU"U'QUB
U"
)U",(U'W'
∂
∂
−
∂
∂
−
−++−=
∂
∂
−−
−−−
;
22
"
д
3
ддд
д
3
д
2
д
д
4
дддд
4
д
2
дд
2
д
U
P
UU'U"
U
Q
UU'
PUU'U"QUU'QUB
U'
)U",(U'W
∂
∂
−
∂
∂
+
++−+−=
∂
∂
−−
−−−
."
"22
"
д
3
д
2
д
д
3
ддд
д
4
д
2
дд
4
дддд
2
д
U
P
UU
U
Q
UU"U'
PUUQUU"U'PUG
U"
)U",(U'W
∂
∂
−
∂
∂
+
++−−=
∂
∂
−−
−−−
В развернутой форме (7.1,б)
;
"''"'
2
'
2
'
'
33
2
44
2
2
i
i
i
ii
i
i
i
i
i
iii
i
ii
i
i
ii
i
i
U
Q
U
UU
U
P
U
U
U
UUQ
U
UP
U
P
g
U
W
∂
∂
−
∂
∂
−−+−=
∂
∂
;
'
'
ij
j
i
g
U
W
=
∂
∂
;
'"'"
2
"'
2
"
'
3
2
34
2
42
i
i
i
i
i
i
i
ii
i
ii
i
iii
i
i
ii
i
i
U
Q
U
U
U
P
U
UU
U
UQ
U
UUP
U
Q
b
U
W
∂
∂
−
∂
∂
−++−=
∂
∂
;
"
'
ij
j
i
b
U
W
=
∂
∂
