McMahon D. String Theory Demystified

Подождите немного. Документ загружается.

246

String Theory Demystiﬁ ed

The Laws of Black Hole Mechanics

In the early 1970s, James Bardeen, Brandon Carter, and Stephen Hawking found

that there are laws governing black hole mechanics which correspond very closely

to the laws of thermodynamics.

The zeroth law states that the surface gravity

the horizon of a stationary black hole is constant.

The ﬁ rst law relates the mass m, horizon area A, angular momentum J, and charge

Q of a black hole as follows:

dm dA dJ dQ=++

ΩΦ

(14.23)

This law is analogous to the law relating energy and entropy. We will see this more

precisely in a moment.

The second law of black hole mechanics tells us that the area of the event horizon

does not decrease with time. This is quantiﬁ ed by writing:

dA ≥ 0

(14.24)

This is directly analogous to the second law of thermodynamics which tells us that

the entropy of a closed system is a nondecreasing function of time. A consequence

of Eq. (14.24) is that if black holes of areas

and

coalesce to form a new black

hole with area

then the following relationship must hold:

AAA

312

As you probably recall, an analogous relationship holds for entropy. Finally, we

arrive at the third law of black hole mechanics. This law states that it is impossible

to reduce the surface gravity

to 0.

The correspondence between the laws of black hole mechanics and

thermodynamics is more than analogy. We can go so far as to say that the analogy

is taken to be real and exact. That is, the area of the horizon A is the entropy S of

the black hole and the surface gravity

is proportional to the temperature of the

black hole. We can express the entropy of the black hole in terms of mass or area.

In terms of mass the entropy of a black holes is proportional to the mass of the black

Bardeen, J.M., B. Carter, and S.W. Hawking, The four laws of black hole mechanics, Comm. Math

Phys. vol. 31, (2), 1973, 161–170.

CHAPTER 14 Black Holes

247

hole squared. In terms of area, the entropy is 1/4 of the area of the horizon in units

of Planck length:

(14.25)

Let us compute the temperature in the case of a Schwarzschild black hole. In the

Chapter Quiz you will get a chance to try your luck ﬁ nding the temperature of a

charged black hole. We follow a procedure outlined in a note published by P.R.

Silva.

We proceed as follows. We perform a Wick rotation

ti→

and write the

Schwarzschild metric as

dr r

=− −

⎛

⎝

⎜

⎞

⎠

⎟

+−

⎛

⎝

⎜

⎞

⎠

⎟

−

ddΩ

(14.26)

Now set

ατ

=−

⎛

⎝

⎜

⎞

⎠

⎟

=−

⎛

⎝

⎜

⎞

⎠

⎟

−

and integrate. We take the limits of integration to be

ααπ

ττβ

≤≤

≤

′

≤rGmrr

This gives us two relations:

22 2

πβ

RGmrGm=−

−

()( )

(14.27)

RGmrGm=−22 2

()( )

(14.28)

Available on the arXiv at http://arxiv.org/ftp/gr-qc/papers/0605/0605051.pdf.

Computing the Temperature of a Black Hole

248

String Theory Demystiﬁ ed

Dividing Eq. (14.27) by Eq. (14.28) we obtain

βπ

⇒=

The

used here is the same one used in thermodynamics, and so we obtain the

following expression for the temperature of a Schwarzschild black hole:

(14.29)

With the temperature in hand, we can proceed ahead to obtain an expression for

the entropy. Recalling that the ﬁ rst law of thermodynamics states that

dE TdS=

(think tedious), using

Emc=

(but taking

c = 1

) we obtain the ﬁ rst law of black

hole mechanics for a static, uncharged black hole:

dm Tds=

(14.30)

Hence,

mdm

dS=

Integrating we ﬁ nd

Hence, the entropy of a Schwarzschild black hole is given by

SGm= 4

(14.31)

This conﬁ rms our earlier claim, that the entropy is proportional to the mass squared.

Before proceeding, let’s quickly refresh our memories. What is entropy anyway?

Suppose that we have a density of states

nE()

for some microscopic system. The

entropy is

Sk nE

= ln[ ( )]

(14.32)

where

is Boltzman’s constant.

CHAPTER 14 Black Holes

249

We will consider two cases, a Schwarzschild black hole where we use a somewhat

loose heuristic estimate and a calculation for a ﬁ ve-dimensional charged black hole.

In string theory, the calculation of the entropy of a black hole is easiest in ﬁ ve

dimensions. This is due to an amazing property of ﬁ ve-dimensional black holes that

arises from supersymmetry. It turns out that supersymmetry allows us to count up

string states while taking the string-coupling constant

= 0

, which amounts to

considering a set of noninteracting strings—something not really possible in a

black hole. This greatly simpliﬁ es the calculation and what is remarkable is that the

result obtained with no coupling is valid for any coupling strength

Remember the adiabatic theorem? The procedure used here is something you

already know about from ordinary quantum mechanics. In quantum mechanics,

you can disturb a system adiabatically so that the energy levels are not disturbed.

The adiabatic method is used here—the string-coupling constant is varied

adiabatically so that large gravitational forces transition to a weak regime. Entropy,

however, is an adiabatic invariant. So while we weaken the string coupling, the

entropy remains the same as long as things are done adiabatically.

In string theory, we start with a collection of highly coupled strings and then let

the coupling

→ 0

slowly. We work in the usual

D =10

space-time of superstring

theory, and need to compactify some extra dimensions to get an effective ﬁ ve-

dimensional space-time. Supersymmetry remains unbroken if we compactify

dimensions into tiny circles. We compactify the dimensions

, ...,

leaving us

with the remaining ﬁ ve-dimensional space-time described by the coordinates

xxxxx

01234

,,,,

. The black hole can actually be thought of as two objects—a

string carrying a charge

and a 5-brane with charge

. These charges are winding

modes as we will see below.

First we consider an adiabatic process

→ 0

applied to a Schwarzschild black

hole in D dimensions. A straightforward calculation using the laws of black hole

mechanics shows that the entropy is given by

−

−−

−

Ω

(14.33)

where

is the mass of the black hole. The entropy can be estimated quite simply

from string theory considerations. For an excited string, the entropy is proportional

to the product of the mass times its length:

∝ C

(14.34)

Entropy Calculations for Black Holes

with String Theory

250

String Theory Demystiﬁ ed

Now let’s use the string theory considerations to ﬁ nd the entropy. This is done by

applying the adiabatic procedure to the string coupling

→ 0

and noting that the

entropy remains unchanged during the process. We follow the procedure outlined

in Susskind (please see References). What is found is that as

→ 0

, the black hole

turns into a single string which has the same entropy as the black hole. The black

hole transitions into a single string when the radius of the horizon is the same as the

fundamental string length

The Planck length

can be related to the fundamental string length using:

−

(14.35)

The Schwarzschild radius of the black hole is given in terms of its mass as

rmG

sBD

−

()

(14.36)

We can approximately take the gravitational constant to be

Dss

≈

−22

(14.37)

So that:

sBs

()

−

(14.38)

We are going to be interested in

C →1

, that is, the point where the

Schwarzschild radius approaches the string length. During the adiabatic process,

the mass becomes a function of the string-coupling constant,

mmg

= ()

. If we take

the initial coupling to be

then

mmg

= (

)

. The entropy is a function of the

product

()C

, and since the entropy is an adiabatic invariant, this product must

be a constant. Using Eq. (14.35) we can write

mg m

()=

⎛

⎝

⎜

⎞

⎠

⎟

−

(14.39)

Now,

C →

when

()CC

−−

which gives

()C =

(14.40)

CHAPTER 14 Black Holes

251

Recalling that the entropy of an excited string is proportional to the product of its

mass and length [Eq. (14.34)], this allows us to write the entropy in terms of the

mass of the black hole and the gravitational constant using [Eqs. (14.39) and

(14.37)]. This gives a result proportional to Eq. (14.33):

Sm G

=∝

−

−−

(14.41)

This calculation was not formal by any means. It just relied on some basic

considerations from string theory, but it gave the correct result modulo a constant.

Now let’s turn to the ﬁ ve-dimensional black hole example.

The structure of the ﬁ ve-dimensional geometry is as follows. We take a circular

dimension of radius R denoted by

and a four torus

so that

TTS

541

=×

As mentioned above, the black hole actually has two string components. One is an

actual string (a D1-brane) which wraps around

and so has winding modes which

will contribute to its mass. The D5-brane wraps around

and also has Kaluza-

Klein modes quantized on the circle

The starting point is the metric given by

ds dt dr r d

22321322

=− + +

(

)

−

λλ

Ω

(14.42)

where:

⎛

⎝

⎜

⎞

⎠

⎟

⎡

⎣

⎢

⎤

⎦

⎥

∏

(14.43)

A result from superstring theory that we simply take as a given because it’s beyond

the scope of our discussion that the BPS condition is satisﬁ ed. What this means

for us is that charges are additive. The upshot of this is we can write the mass of

the black hole as

MM M M=++

123

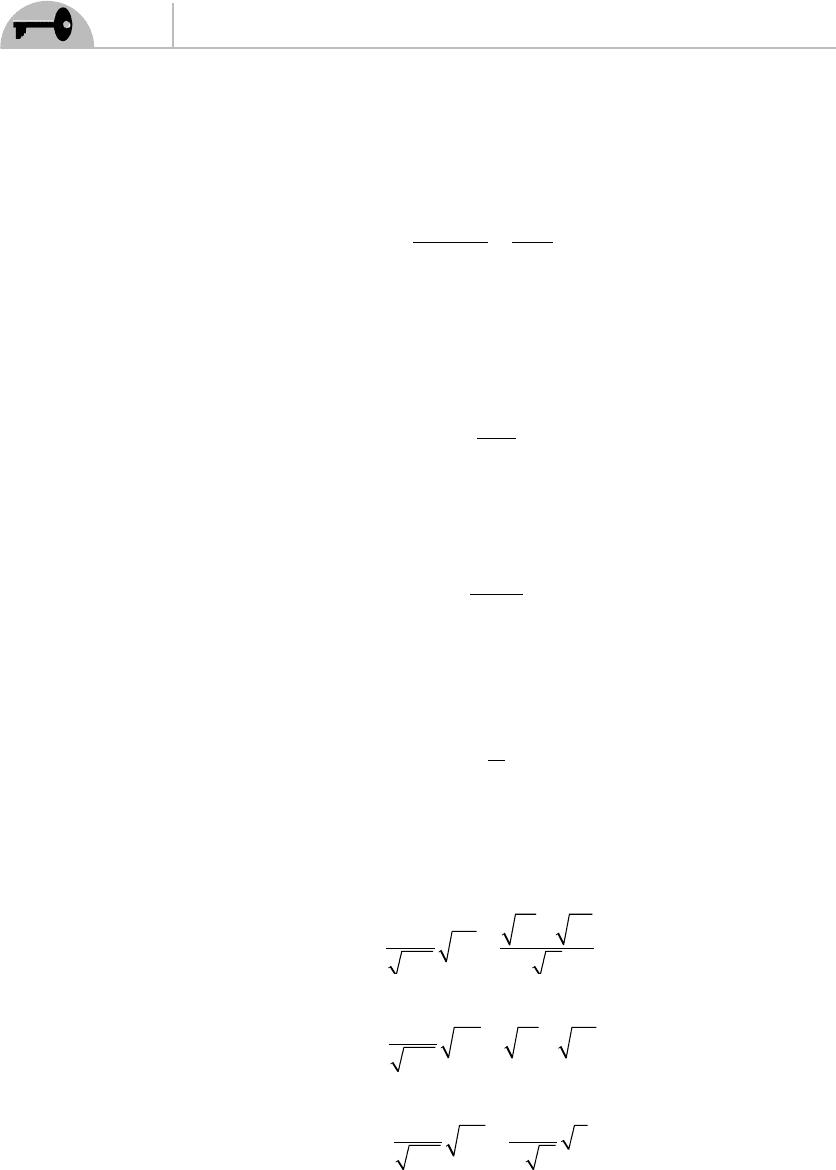
252

String Theory Demystiﬁ ed

Now the calculation of the entropy is actually quite straightforward. From the

metric in Eq. (14.42), there are three radii associated with the horizon. Using

Eq. (14.9) with

D = 5

, we can write each of these as

mG g

Ω

(14.44)

where

is the radius of the circular dimension

and

is the volume of the torus.

The individual masses can be calculated from string considerations. The ﬁ rst two

masses are due to winding modes. First, the string winding around radius R gives

(14.45)

For the D5-brane, ﬁ rst we have the winding mode which wraps around the circle

and torus:

QRV

(14.46)

Then we have a third mass, due to the Kaluza-Klein excitation of the D5-brane

along the circular dimension:

(14.47)

Now let’s calculate each of the radii:

(14.48)

mgQ

ss2

(14.49)

ss ss

(14.50)

CHAPTER 14 Black Holes

253

Now, the area in ﬁ ve dimensions is

Arrr

QQn

==22

123

ππ

The entropy is

(14.51)

where

GGRV g

ss5

5628

228==() ()

πππ

. Putting everything together we obtain

the result:

SQQn= 2

(14.52)

One of the recent successes of string theory has been its ability to count up the

microscopic states of a black hole to calculate its entropy. The result obtained in

this manner agrees with the semiclassical expressions, providing strong support for

string theory as a quantum theory of gravity.

Quiz

1. Find the temperature of a D = 4 charged black hole.

2. The Hagedorn temperature is the temperature above which multiple strings

would coalesce into a single string. Take the density of string states to be

nm=

′

exp( )4

πα

and write down the partition function. What condition

is necessary for the partition function to be ﬁ nite? This gives the Hagedorn

temperature.

3. Suppose that the sun were to collapse to a black hole. What would be its

temperature?

4. Estimate the lifetime of a six solar mass black hole that is evaporating from

the Hawking process.

Summary

254

String Theory Demystiﬁ ed

5. Consider a charged, rotating black hole in D = 5 dimensions with metric:

ds dt

223

=− − +

⎛

⎝

⎜

⎞

⎠

⎟

−

λθφθψλ

sin cos

113 2 2

dr r d

()

Ω

By calculating the area of the horizon, estimate the entropy. Take the

charges to be the same as for the static charged black hole analyzed in the

text.

The Holographic

Principle and AdS/CFT

Correspondence

In this chapter we will touch on one of the most interesting ideas to come out of the

study of quantum gravity and string theory in particular: the holographic principle.

This is an idea closely related to entropy, so we present it here after we have

completed our discussion of black holes and entropy in the last chapter. The

holographic principle appears to be a quite general feature of quantum gravity, but

we discuss it in the context of string theory. Our discussion largely follows that of

Susskind and Witten.

Our focus will be on showing how the holographic principle

leads to an entropy bound of the type we found for black holes.

CHAPTER 15

The topics discussed here are quite advanced, so our discussion will be more qualitative and heuristic.

For a detailed exposition you may consult L. Susskind and E. Witten, “The Holographic Bound in Anti-

de Sitter Space,” http://xxx.lanl.gove/abs/hep-th/9805114; and J. M. Maldacena, “The Large N Limit of

Superconformal Field Theories and Super Gravity,” Adv. Theor. Math. Phys. 2:231–252, 1998.