Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

642 Vb. Two-Phase Flow and Heat Transfer: Boiling

2.1. Dimensionless Groups

Practical aspects of boiling heat transfer are based on experimental data. To corre-

late such data we need to find the dominant factors in heat transfer associated with

phase change. Such factors include the involved forces, key fluid properties, and

the operational conditions. Viscous and buoyancy forces play a major role in heat

transfer with phase change. Pertinent fluid properties include latent and specific

heat (h

, c

), density and thermal conductivity (

, k), and viscosity and surface

tension (

). Finally, operational conditions include pressure, fluid and surface

temperature, and the surface geometry (L). Since the effect of pressure appears in

fluid properties, we can reduce the number of variables to 10. These are

, h

, k,

, ∆T, L and h. Incropera finds five dimensionless groups for these pa-

rameters; Nu = hL/k = f[

–

, Ja, Pr, Bo] where the Bond number (Bo)

is similar to the Gr number (Table A.I.6).

2.2. Determination of Degree of Superheat

for Equilibrium Bubble

Homogeneous nucleation: Earlier we noticed that for a bubble to be in equi-

librium in the bulk of a liquid, three conditions must be met. To maintain equilib-

rium, we can use these conditions to find the minimum degree of superheat for a

liquid; i.e. T

– T

sat

. From the requirement for equal chemical potential, we obtain

the Clausius-Clapeyron equation dP/dT = h

/(T

sat

). We integrate this equation

assuming T

sat

remains constant. We then substitute for P

– P

= 2

from

the second requirement to find:

egfg

sat

efg

fgsat

satl

TTT

≅

=∆=−=∆

Vb.2.1

where r

is the radius of the equilibrium bubble. Equation Vb.2.1 shows that the

degree of superheat is inversely proportional to the bubble radius. Thus, the

smaller the bubble, the higher the required degree of superheat. That is why the

homogenous nucleation requires very high degrees of superheat.

Heterogeneous nucleation: Regarding nucleation from a heated surface, we

noticed that the minimum radius of a growing bubble is when r

= r

, where r

the radius of the cavity. Substituting into Equation Vb.2.1, we conclude that bub-

bles that have made it to the mouth of the cavity will grow if the degree of super-

heat in the liquid is at least equal to ∆T as given by Equation Vb.2.1. This is in-

deed the case if the bulk liquid is superheated. Superheating is achieved by

heating the liquid in a pressurized vessel until liquid becomes saturated. When the

heating process is terminated and the vessel is perfectly insulated, we reduce the

liquid pressure. As the pressure drops, bubbles begin to form on the surface of the

vessel when the liquid superheat becomes at least equal to that given by Equa-

tion Vb.2.1.

2. Convective Boiling, Analytical Solutions 643

sat

T(y)

Thickness of

Thermal Sublayer

Solid

Vapor

Liquid

Bubble

Thermal

Sublayer

(a) (b)

Figure Vb.2.1. Heterogeneous boiling and temperature gradient in liquid

It is fascinating to note that if boiling is induced solely by continuing to heat the

vessel, the degree of superheat required for boiling is much higher than that pre-

dicted by Equation Vb.2.1. Indeed, some data have shown that the required de-

gree of superheat for bubble growth is three times as much as that predicted by

Equation Vb.2.1 (Hsu). The reason turns out to be the existence of a region (Fig-

ure Vb.2.1) referred to as the thermal sub-layer. Liquid temperature increases

markedly in this region from T

sat

to T

, Figure Vb.2.1(b). It is in this thermal sub-

layer near the heated surface that liquid becomes superheated to provide sufficient

heat for the bubble to grow and depart.

We may estimate the thickness of the thermal sub-layer by using the definition

of heat transfer coefficient (h). Thus, the thickness of the thermal sub-layer is re-

lated to the liquid thermal conductivity as

= k

/h where h can be estimated from

a correlation such as that of Fishenden for turbulent natural convection from a

horizontal flat surface:

()

3/1

PrGr14.0Nu =

where the Gr and Pr numbers are calculated for the liquid phase. Next, we focus

on the heat transfer mechanism taking place in the thermal sub-layer.

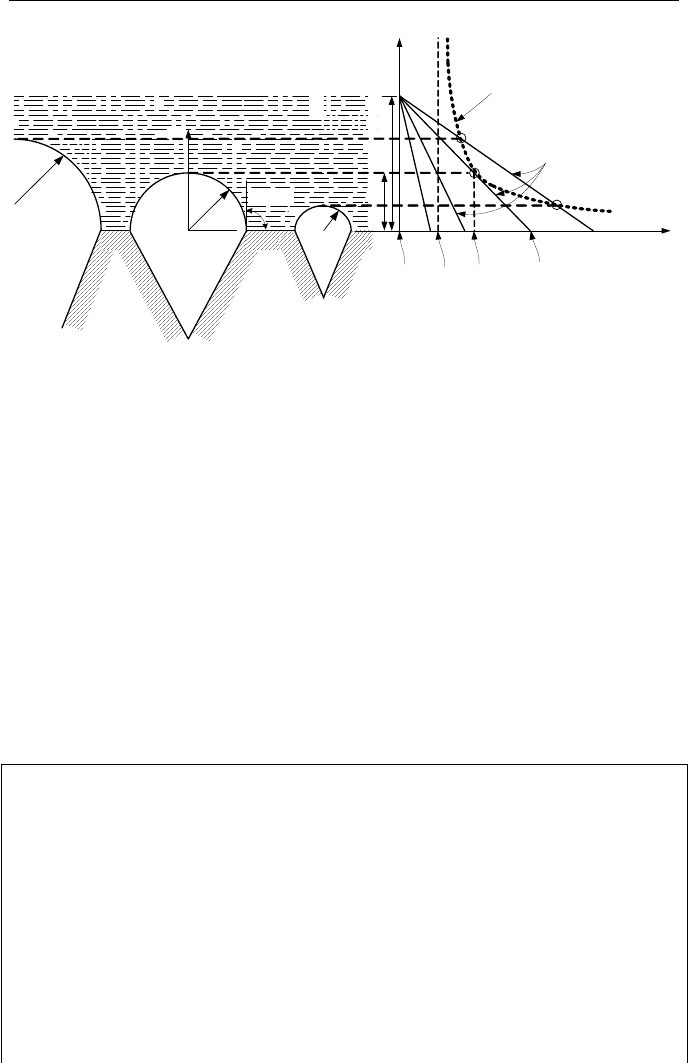
Let’s investigate the relation between the bubble equilibrium temperature

(Equation Vb.2.1) and water temperature in the thermal sub-layer. Shown in Fig-

ure Vb.2.2 is a cavity of radius r

on the heated surface.

Originally, both liquid and surface have the same temperature as the bulk liquid

(line ZO). We add heat to the surface and bring its temperature to T

. The tem-

perature in the thermal sub-layer is shown by line ZA where we have assumed a

linear temperature profile in the thermal sub-layer. Since we do not observe any

bubble in the liquid we increase the surface temperature to T

with the liquid tem-

perature shown by line ZB. As we heat up the surface, the bubble in the cavity

begins to grow. We keep increasing the surface temperature until eventually the

line representing temperature in the thermal sub-layer (line ZC) becomes tangen-

tial to the curve representing Equation Vb.2.1 for an equilibrium bubble. At this

point, the bubble in the cavity has reached the mouth of the cavity and has the

smallest radius of curvature. Hsu’s condition for the bubble to grow is that the

644 Vb. Two-Phase Flow and Heat Transfer: Boiling

sat

Equation Vb.2.1

Liquid Temperature

max

min

ONB

=90

min

max

Figure Vb.2.2. Depiction of the onset of nucleate boiling (Hsu)

liquid temperature at y = r

must be at least equal to the bubble interior tempera-

ture for the bubble to grow. Thus, when the line for liquid temperature is tangent

to the curve representing the equilibrium bubble (Equation Vb.2.1), cavities of ra-

dius r

are active sites for nucleation. The corresponding temperature, is known as

onset of nucleate boiling temperature (T

ONB

If the surface temperature is further increased (say to T

corresponding to line

ZD for the thermal sub-layer), then at lower superheats the larger radii cavities and

at higher superheats smaller radii cavities become active. But if a cavity of size r

does not exist on the surface, the increasing surface temperature results in higher

degrees of liquid superheat. This will continue until the temperature profile in liq-

uid becomes tangent to the vapor temperature calculated from Equation Vb.2.1 for

the cavity size that is present in the surface. When various cavity sizes exist and

the bulk liquid is at saturation, we may approximate r

as r

/2. Using similar

triangles, we find that (

– r

)/r

= ∆T

sat

/∆T

ONB

resulting in ∆T

ONB

= 2∆T

sat

Example Vb.2.1. Find the degree of superheat (T

– T

sat

) for a horizontal flat

plate in water at atmospheric pressure necessary to cause nucleation at all active

sites. Data: At 1 atm,

= 958 kg/m

= 0.593 kg/m

, h

= 2.257E3 kJ/kg, k

0.68 W/m·C,

= 0.059 N/m,

= 0.75E-3 C

-1

, v = 0.292E-6 m

/s, Pr = 1.73.

Solution: We first find the thickness of the thermal sub-layer in terms of ∆T

, the

surface temperature minus the saturation temperature:

Gr =

g∆T

= [0.75E-3 × 9.81 ∆T

/(0.292E-6)

] = 8.63E10 ∆T

hD/k

= 0.14Gr

1/3

= 0.14 [8.63E10 ∆T

]

1/3

(1.73)

1/3

= 743 (∆T

)

1/3

Since

= k

/h, we find:

= 743 (∆T

)

1/3

. Therefore,

= 1.35E-3(∆T

)

–1/3

m. (1)

2. Convective Boiling, Analytical Solutions 645

Next, we find the required surface superheat, ∆T

= T

– T

sat

from Equation Vb.2.1:

∆T

= 2

sat

/(h

) = 2 × 0.059 × (100 + 273)/(2.257E6 × 0.593 × r

) = 3.3E-5/r

(2)

Substituting for r

= r

/2 into (2) yields: ∆T

= 6.6E-5/

. Substituting ∆T

into

(1) to find

as:

= 1.35E-3[6.6E-5/

)

-1/3

. We, therefore, find

= 6 mm. Thus, ∆T

= 0.019 C.

Comment: It is seen when cavities of all sizes are present, the required degree of

superheat is very small.

Let’s assume only cavities of 8

m exist. In this case, r

= 8E-6 m and (∆T

)

required

= 3.3E-3/8E-6 = 4 C.

Heterogeneous nucleation formulation: We now want to quantify our quali-

tative argument regarding the vapor temperature and the thermal sub-layer tem-

perature. For this purpose we find the equation for liquid temperature in the ther-

mal sub-layer and set it equal to the vapor temperature in the bubble as given by

Equation Vb.2.1. This method was originally suggested in 1962 by Hsu. Since

the thermal sub-layer is thin, we use a linear temperature profile in this region

which must satisfy the following boundary conditions:

At y = 0, T(y = 0) = T

and at y =

, T(y =

) = T

where T

and T

are the surface and the free stream temperatures of the bulk liquid,

respectively. The profile is obtained as:

−

Vb.2.2

We make a change of variable from y with r

(See Figure Vb.2.3) to obtain:

y = c

= (1 + cos

Vb.2.3

We now set Equation Vb.2.1 equal to Equation Vb.2.2, while substituting for y

from Equation Vb.2.3.

Figure Vb.2.3. Depiction of bubble height, radius, and cavity radius

646 Vb. Two-Phase Flow and Heat Transfer: Boiling

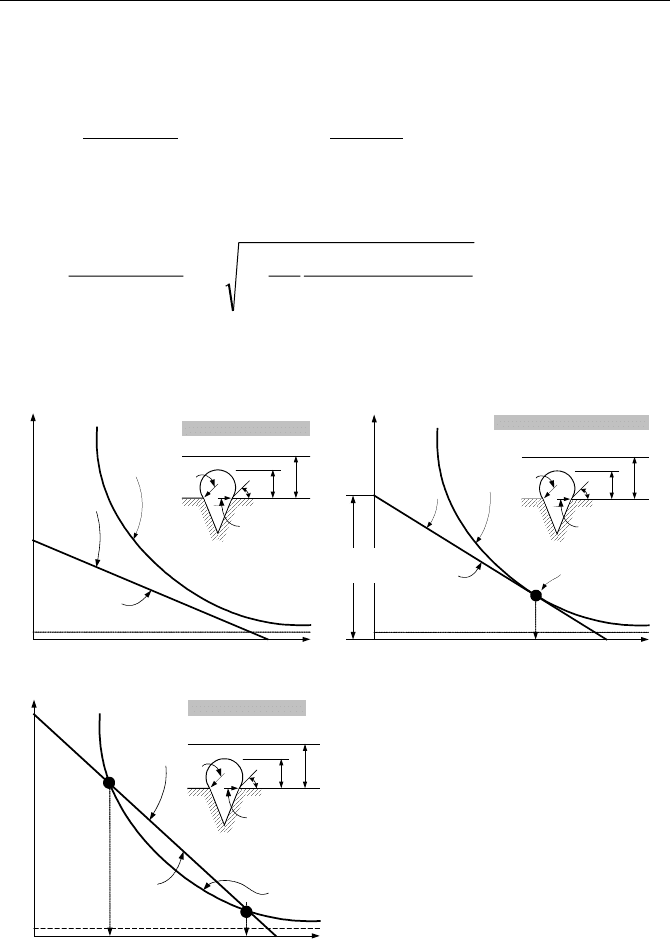
Depending on the boiling condition, the curves representing the two temperature

profiles may a) not meet, b) be tangent to each other, or c) intersect at two loca-

tions. These conditions are obtained from the solution to the following equation:

fsf

cgfg

sat

TTT

rch

)(

2 −

−+=+

This results in a second order algebraic equation for r

. The solution is found as:

−

−±

−

fggsats

satfs

sats

hTT

TTT

TTc

δρ

)(

)(2

)(

Vb.2.4

The results are plotted in Figure Vb.2.4.

sat

Liquid

temperature

profile

Bubble

temperature

profile

′′

No Nucleate Boiling

sat

Liquid

temperature

profile

Bubble

temperature

profile

′′

Boiling

Inception

∆T

ONB

Onset of Nucleate Boiling

sat

Liquid

temperature

profile

Bubble

temperature

profile

′′

Nucleate Boiling

Figure Vb.2.4. Comparison of the vapor bubble and liquid temperature profiles

These concepts are further developed in Chapter VIe.

2. Convective Boiling, Analytical Solutions 647

2.3. Prediction of Bubble Growth

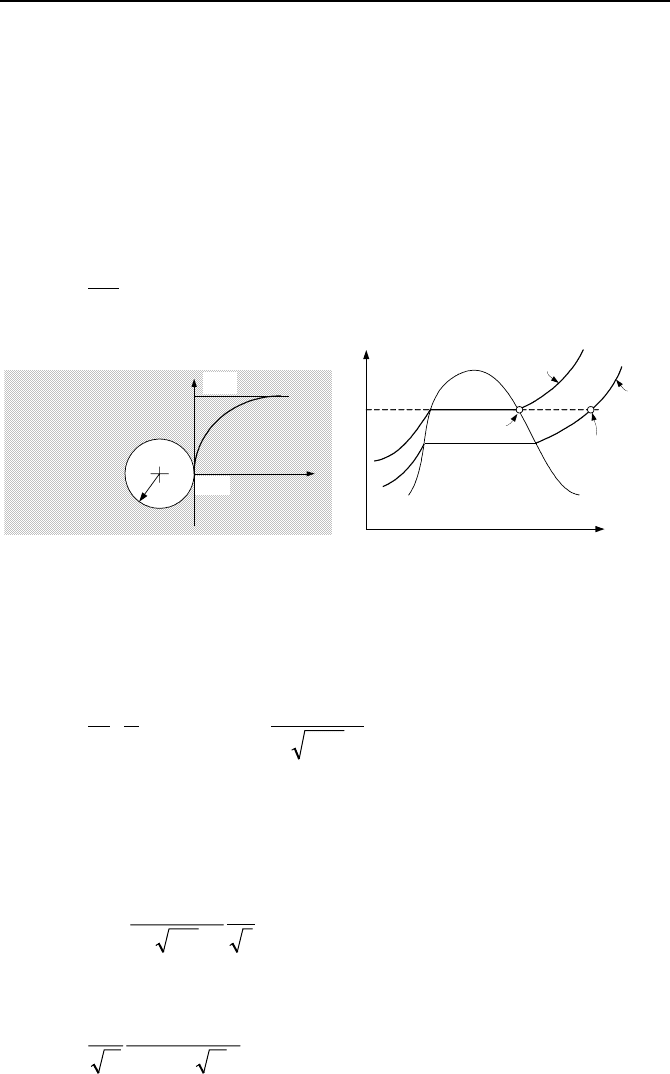
We can predict the growth rate of a vapor bubble rather accurately by treating the

surrounding superheated liquid as a semi-infinite body. In this case, the specified

boundary condition is heat flux at the interface between the liquid and the vapor

bubble, as shown in Figure Vb.2.5. Since liquid is being cooled at the interface

we can write the following energy balance:

Rate of increase in bubble internal energy = Rate of liquid cooldown at the inter-

face

()

fgg

′′



πρ

Liquid

T = T

sat

sup

sat

Bubble

Liquid

sat

sup

Bubble

Liquid

Bubble

Liquid

Figure Vb.2.5. Growth of a vapor bubble in the pool of superheated liquid

Substituting for heat flux at the interface from Equation IVa.9.10 and for volume

in terms of radius yields:

()

TTk

fgg

πα

ππρ

)(

−

Note in this case, the semi-infinite body is initially at T

= T

sup

when the interface

is suddenly cooled to T

= T

sat

. Subscripts sup and sat stand for superheated and

saturated, respectively. Carrying out the derivative, canceling similar terms

) from both sides of the equation, and rearranging, we obtain:

TTk

dRh

fgg

πα

)( −

Using the initial condition of R = 0 at t = 0, we find:

(

)

2/1

sup

)( t

TTk

fgg

sat

αρπ

−

Vb.2.5

648 Vb. Two-Phase Flow and Heat Transfer: Boiling

As Lienhard describes, Jakob initially suggested the method that led to the deriva-

tion of Equation Vb.2.5. As shown in Figure Vb.2.4, this equation under-predicts

the data obtained by Dergarabedian. Hence, Scriven used a more rigorous method

and found that R

bubble

= 3 R

Jakob

, which closely matches the data.

Figure Vb.2.6 shows that the trend predicted by Jakob is as expected but the

absolute value under-predicts the data. The reason is that the bubble growth in-

creases the temperature gradient, which has been treated as constant in Jakob’s

model. Scriven accounts for this and practically matches the data.

0.005 0.01 0.013

0.8

0.4

0.0

Time (s)

Bubble Radius (mm)

Data

sup

- T

sat

= 3.1 C

Scriven

Jakob

Figure Vb.2.6. Comparison of R

Jakob

and R

Scriven

with data

Example Vb.2.2. Find the bubble diameter 0.01 s into the bubble growth for wa-

ter boiling at 1 atm and ∆T = 3 C. Data: k

= 0.68 W/m·K,

= 0.593 kg/m

1.68E-7 m

/s, and h

= 2.257E6 J/kg.

Solution: From Equation Vb.2.5, we find R(0.01 s) as:

(

)

2/1

sup

)(

TTk

fgg

sat

αρπ

−

4336.03E101.0

7E68.16E257.2593.0

1.368.02

=×

−×

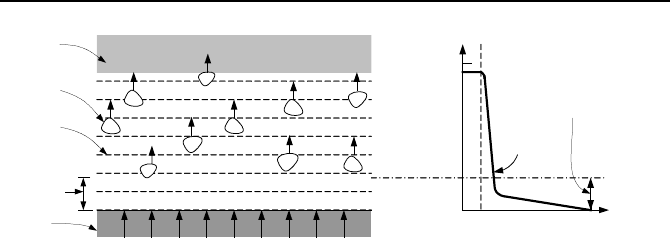
3. Convective, Boiling, Experimental Observation

Before discussing the two distinct modes of pool and flow boiling, we consider the

landmark experiment performed by Nukiyama in 1934, which led to the estab-

3. Convective, Boiling, Experimental Observation 649

lishment of the boiling curve. The importance of this curve is in its clear depiction

of various modes of heat transfer and demonstration of the effect of the method of

heat addition to the liquid. This was the first experiment for the measurement of

surface heat flux versus surface superheat (∆T

= T

– T

sat

). As shown in Fig-

ure Vb.3.1(a) the experiment consists of an electrically heated wire in a water con-

tainer at atmospheric pressure. Nukiyama used a nichrome wire connected to an

electric voltage. Data were obtained by varying the electric power measuring wire

temperature after steady-state is achieved. This is referred to as power-controlled

or heat flux controlled heating where

′′



is the independent variable and surface

temperature (hence ∆T

= T

– T

sat

) is the dependent variable. As power increased,

there was a sudden jump in the wire temperature and eventual burnout. The heat

up path is shown in Figure b with the arrows. The cool down path was obtained

by reducing electric power to the wire as shown in Figure c by the arrows. As

these figures indicate, on both heat up and cooldown paths, there is a jump from

one side of the curve to the other. This is typical of power-controlled heat up and

cooldown. Figure d shows how the entire boiling curve can be constructed if the

process is temperature-controlled. In this case, there is a specific heat flux for a

specific wall temperature. In practice, most processes such as production of heat

in the core of nuclear reactors are power-controlled. As a results, in such applica-

tions, care must be exercised no to exceed the maximum heat flux as damage to

the surface would follow.

Water

Vapor

Wire

∆T

′′

(a) (b)

∆T

′′

∆T

′′



(b) (d)

Figure Vb.3.1. Nukiyama experiment for developing the boiling curve

650 Vb. Two-Phase Flow and Heat Transfer: Boiling

4. Pool Boiling Modes

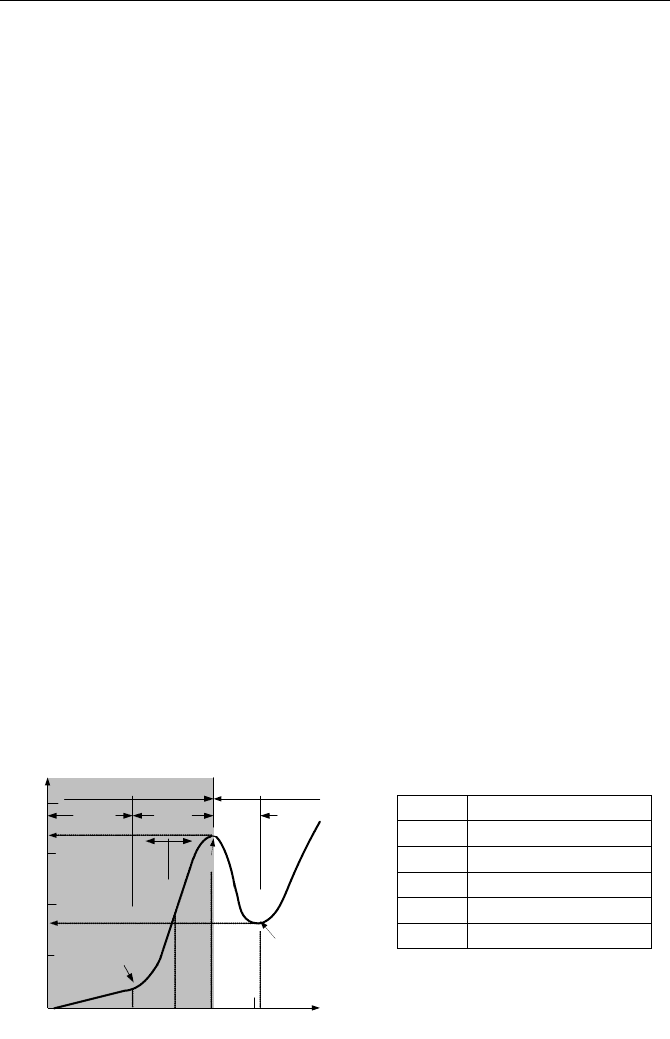
The boiling curve for pool boiling heat transfer at atmospheric condition is shown

in Figure Vb.4.1. Temperature is in degrees centigrade. Since the bulk liquid is

quiescent, there is no heat flux when ∆T

= 0. With an increasing degree of su-

perheat, the surface heat flux increases solely due to free convection. At about

∆T

= 5 C, the bubbles begin to grow and some may depart the surface. The

buoyancy driven bubble causes agitation in the liquid. This mixing of liquid en-

hances heat flux. With increasing ∆T

, more bubbles are formed and the rate of

carrying energy from the surface to the bulk liquid increases. Eventually, the rate

of bubble production becomes so great that at ∆T

about 30 C, heat flux reaches

its peak value. Beyond this point, the bubble population is so dense that it pre-

vents liquid from reaching the surface. When this happens, heat transfer takes

place only by conduction through the layer of vapor, which has blanketed the sur-

face. With the surface being deprived of an efficient means of heat transfer by

boiling bubbles, surface temperature jumps to elevated values. With heat flux

maintained at its peak value, the jump in the surface temperature compensates for

the sudden drop in the heat transfer coefficient. The heat transfer regime with va-

por blanketing the surface is referred to as film boiling. The peak heat flux is re-

ferred to as the critical heat flux (CHF). A modest increase in heat flux beyond

the CHF is due to both conduction through the vapor film and radiation due to the

surface elevated temperature. On the cool down path, the reverse process occurs.

When ∆T

reaches around 100 C, the vapor production is not vigorous enough to

keep liquid away from the surface. With liquid in contact with the surface, the ef-

ficient heat transfer resumes. The point at which liquid contacts the surface again

is known as the minimum stable film boiling (MSFB) or the Leidenfrost point. In

1756 Leidenfrost observed droplet boil off on hot surfaces. For surface tempera-

ture-controlled processes, the path between CHF and MSFB can be constructed.

In this path, liquid and surface contact intermittently. This mode is known as

transition boiling.

∆T

(C)

MSFB

CHF

ONB

max

′′

min

′′

Post-CHFPre-CHF

Forced

Convection

Nucleate

Boiling

Film

Boiling

100

SB BB

1E3

1E4

1E5

1E6

MSFB Min. Stable Film Boiling

CHF

ONB

Critical Heat Flux

Onset of Nucleat Boiling

Transition Boiling

BB Bulk Boiling

Subcooled Boiling

Figure Vb.4.1. The boiling curve for water at 1 atm and various heat transfer regimes

4. Pool Boiling Modes 651

4.1. Nucleate Pool Boiling

Rohsenow, in 1952, obtained the nucleate pool boiling correlation in the form of

Ja = f(Re, Pr). The Reynolds number was defined for the bubbles as Re = G

where G

is bubble mass flux, D

is bubble diameter, and

is liquid viscosity.

Therefore, c

p,f

∆T/h

= C

s,f

)

. Rohsenow introduced C

s-,f

, r, and n so

that nucleation on a variety of heated surfaces and liquids can be represented by

the same relation. Expressing the bubble diameter in terms of contact angle, sur-

face tension, and fluid density as D

= 1.48

[2g

/(g∆

)]

0.5

and the bubble mass

flux in terms of G

= q

′′



, we find:

0.33

()

()Pr

ssat

ffg ffg f

cTT

hgh

µρρ

−

ªº

«»

¬¼

−



Vb.4.1a

Solving for heat flux:

5.0

)()(

−

′′

ffgsf

satsfpgf

fgf

TTcg

ρρ



Vb.4.1b

The values for coefficient C

and n for various surfaces and liquids are given in

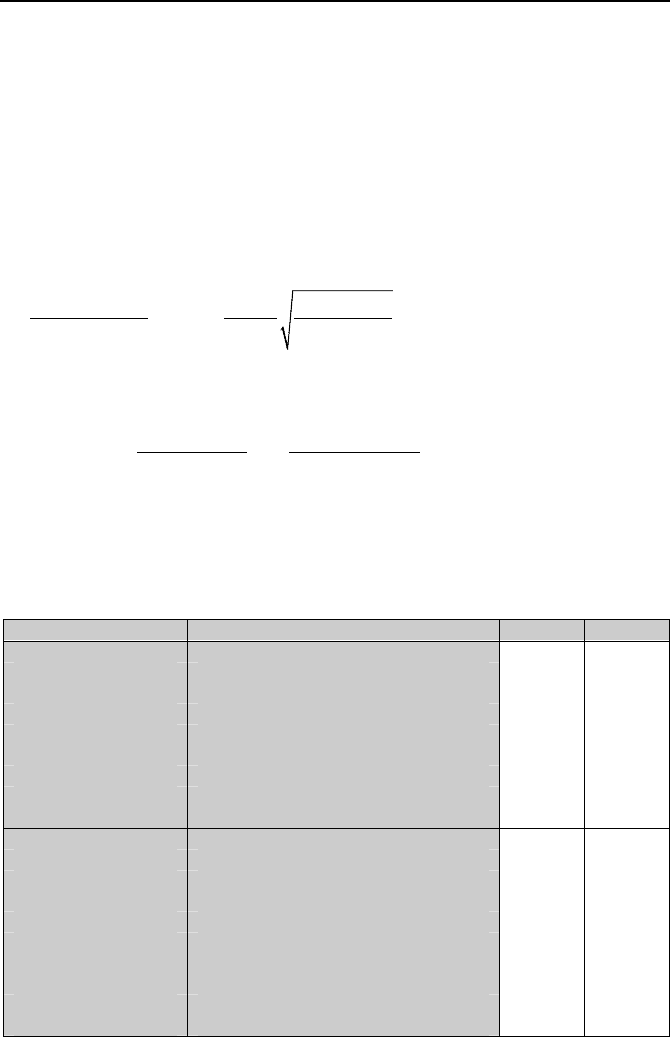
Table Vb.4.1.

Table Vb.4.1. Values for coefficients C

and n for various liquid and surfaces

Fluid Surface C

Benzene Chromium 0.1010 1.7

Carbon tetrachloride Copper, polished 0.0070 1.7

Ethyl alcohol Chromium 0.0027 1.7

Isopropyl alcohol Copper 0.0025 1.7

n-Butyl alcohol Copper 0.0030 1.7

n-Pentane Copper, polished 0.0154 1.7

Nickel, polished 0.0127 1.7

Copper, emery-robbed 0.0074 1.7

Chromium 0.0150 1.7

Water Brass 0.0060 1.0

Copper, polished 0.0128 1.0

lapped 0.0147 1.0

scored 0.0068 1.0

Nickel 0.0060 1.0

Stainless steel, ground & polished 0.0080 1.0

, Teflon pitted 0.0058 1.0

, chemically etched 0.0133 1.0

, mechanically polished 0.0132 1.0

Platinum 0.0130 1.0