Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

8. Applications of the First Law, Transient 81

Water



Feedwater is Subcooled Feedwater is Saturated

Water

Control

Volume

Saturated

Steam



Steam

Control

Volume

(a) (b) (c)

Figure IIa.7.4. Adding heat to a vessel at constant pressure

From the conservation equation of mass for steady flow and steady state condi-

tions,

mmm



== . Also from the conservation equation of energy,

eeiii

hmQhm



=+ . Therefore, the steaming rate is found as:

hPh

−

)(



IIa.7.1

As shown in Figure IIa.7.2-c, if the feedwater is saturated at pressure P (h

= h

Equation IIa.7.1 reduces to:

)(Ph



= IIa.7.2

Note that, for a given rate of heat transfer, the steaming rate at a higher pressure is

higher than the steaming rate at a lower pressure. This is due to the decrease in

the latent heat of vaporization of water as pressure increases (Figure IIa.3.4).

8. Applications of the First Law, Transient

In practice, prior to establishment of steady state conditions, unsteady state or

transient operation prevails. Transient operation can also be imposed on a system

operating at a steady state condition. Consider for example, the steady flow of

steam in a pipe when a fully open valve is throttled to a new partially open posi-

tion. The flow of steam goes through a transient to reach a new steady state con-

dition corresponding to the new position of the valve. We solve transient prob-

lems similar to problems for steady state condition by using the conservation

equations of mass and energy as well as the equation of state. For a process that

brings the control volume from state 1 at time t

to state 2 at time t

, we find the

mass at state 2 by integrating Equation IIa.5.1:

82 IIa. Thermodynamics: Fundamentals

)]()([

tmtmdtmdtm

outlet

inlet

−+

¦¦



IIa.8.1

Example IIa.8.1. Water is flowing in a 6 cm inside diameter pipe at a velocity of

0.75 m/s. The pipe discharges into an initially empty tank having a volume of 0.3

. How long will it take to fill the tank?

Solution: We first find the mass flow rate of water at atmospheric condition (v =

0.001 m

/kg) as:



VA/v = 0.75 × [

(0.06)

/4]/0.001 = 2.12 kg/s.

From Equation IIa.5.3 we have; dm/dt =

outin



− = 2.12 – 0 = 2.12 kg/s.

Hence, dm = 2.12dt. Integrating: m

– m

= 2.12t. Since m

= 0, and m

= V

tank

/v =

0.3/0.001 = 300 kg, we find t = 300/2.12 = 141 s.

Similarly, we find the internal energy of the control volume at state 2 by inte-

grating Equation IIa.6.4:

22 11

[ ( )( ) ()()]

tt tt

inlet inlet

tt tt

tttt

see

ioutlet

mh dt Q dt

Wdt mhdt mtut mtut

´´

µµ

¶¶

´´

µµ

¶¶

§·§·

¨¸¨¸

©¹©¹

§·

++−

¨¸

©¹ © ¹

¦¦



IIa.8.2.

ignoring changes in the K.E. and P.E. In the following examples, simple transient

cases involving filling and draining containers are discussed. These include both

cases of liquid and gas.

8.1. Dynamics of Mixing Tanks

Shown in Figure IIa.8.1 is a simple case of simultaneous filling and draining a

heated mixing tank at atmospheric pressure. The tank is fed through several inlet

ports. The shaft work is performed by the mixer and a heater may add heat to the

water in the tank. Using the conservation equations of mass and energy, we can

obtain two parameters in terms of other known data. For example, if the inlet

mass flow rates, inlet enthalpies, mixer power, and the heater power are specified,

we can solve for the mass and temperature of the tank water versus time. To per-

form this analysis, we make several assumptions: a) negligible K.E. and P.E.

changes, b) perfect and instantaneous mixing, c) subcooled water in the tank

throughout the process, d) no chemical reactions, e) no heat loss from the tank,

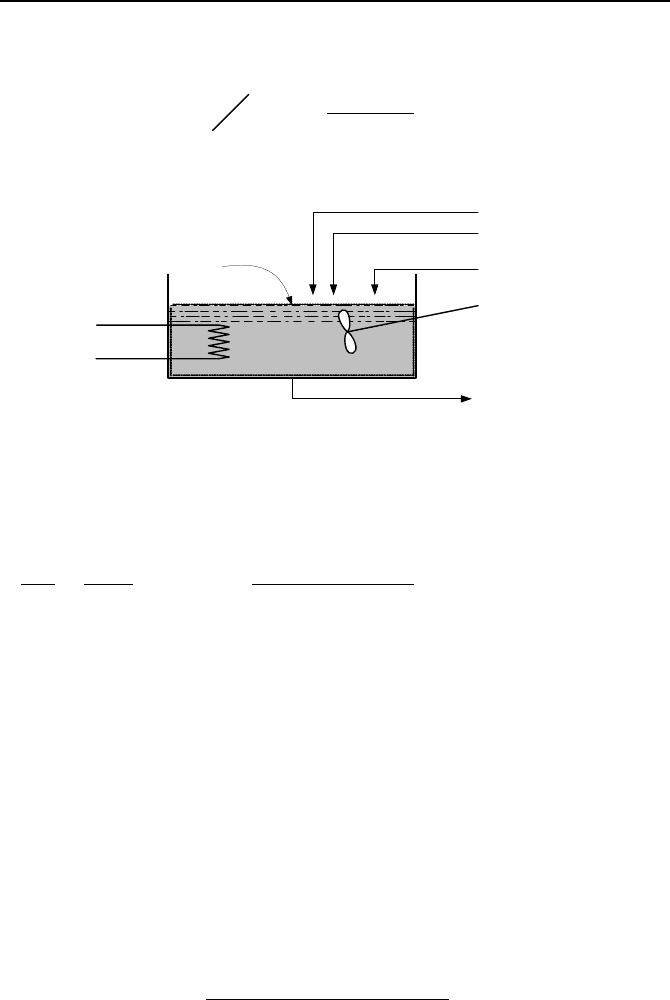
8. Applications of the First Law, Transient 83

and f) constant tank pressure throughout the process. Applying these assumptions,

Equation IIa.6.4-1 becomes:

mhd

hmPWQhm

ees

)(

V +++−=+







)(),(

thtm



)(),(

thtm



)(),( thtm



)(),( thtm



Instantaneous & Perfect Mixing

Q(t)



(t)



(Heater)

(Mixer)

(Inlet Ports)

(Exit Port)

Control Volume

)(

tfm

Figure IIa.8.1. Schematic of a simple mixing tank

We now take the derivative of the last term in the right side and substitute from

Equation IIa.5.1 to find

iis

hmWQ

mdt



IIa.8.3

where we used the perfect mixing assumption, which implies that h

= h

C.V.

. The

mass of water in the tank is a function of time. For example for constant mass

flow rates into and out of the tank, Equation IIa.5.1 predicts that the tank water

mass varies linearly with time:

() ( )

tmmmm

−+=



whre (m

)

C.V.

is the initial mass of water in the tank. Upon substitution of (m)

C.V.

into Equation IIa.8.3, we obtain a linear first-order differential equation for h

. A

general solution to such differential equations is given by Equation VIIb.2.4. De-

pending on the complexity of the functions representing the heater power, the

shaft work, the inlet and exit mass flow rates, we may have to resort to numerical

solutions, from which we obtain:

Explicit:

()

hhmWQ

∆

−++



;

84 IIa. Thermodynamics: Fundamentals

Implicit:

()

+∆

−++

mtm

hhmWQ



where n is a time step index. In the above solution, a semi-implicit scheme is used

(see Chapter VIIe and Problem 101).

Recall that for subcooled water dh

≅ c

dT. Assuming constant specific heat

and substituting in the explicit scheme, for example, we find the water temperature

at every time stop as:

()

nn nnn

siie

QW mT T

mtc

++ −

∆



IIa.8.4

Example IIa.8.2. Flow enters a fully insulated tank from two inlet ports and

leaves through one outlet port. Find water level in 30 minutes. Assume instanta-

neous and perfect mixing. Tank volume is 100 ft

, cross sectional area is 10 ft

initial water volume is 5 ft

, and initial water temperature in the tank is T

tank

100 F.

Control Volume

= 1 lbm/s

A = 0.03 ft

V = 1.00 ft/s

P = 15.0 psia

T = 150.00 F

A = 0.04 ft

V = 0.65 ft/s

P = 15.0 psia

T = 200.00 F

water

= 5.0 ft

water

= 100 F

(h = 168.09 Btu/lbm)

tank

= 10.0 ft

tank

= 100 ft

(h = 117.98 Btu/lbm)

Solution: To find water level as a function of time, we first need to find water

volume by dividing the mass of water by the density of water in the tank. Water

level is then obtained by dividing water volume by the tank cross sectional area.

Since there is no heat or work transfer to or from the control volume, temperature

of water at each time step is found from the simplified form of Equation IIa.8.4:

()

11 1 1 2 2 2 2

() ()

VA T T V A T T

mtc

ρρ

−+ −

∆

where we assumed constant specific heat. Initially (i.e., at time zero n = 0), the

temperature, mass, and level of the tank water are

0=n

T = 100 F, m

n= 0

= 5 ft

62 lbm/ft

= 310.56 lbm, and L

n = 0

= 0.5 ft, respectively. We now choose a time

step size of ∆t = 0.1 s, for example, and find

1=n

T at t = 0 + 0.1 = 0.1 s. Having

found

1=n

T , we proceed to find

2=n

T for time t = 0.2 s. We continue this process

until t = 1800 s. The FORTRAN program representing the numerical solution is

included on the accompanying CD-ROM. From the program we find that in 30

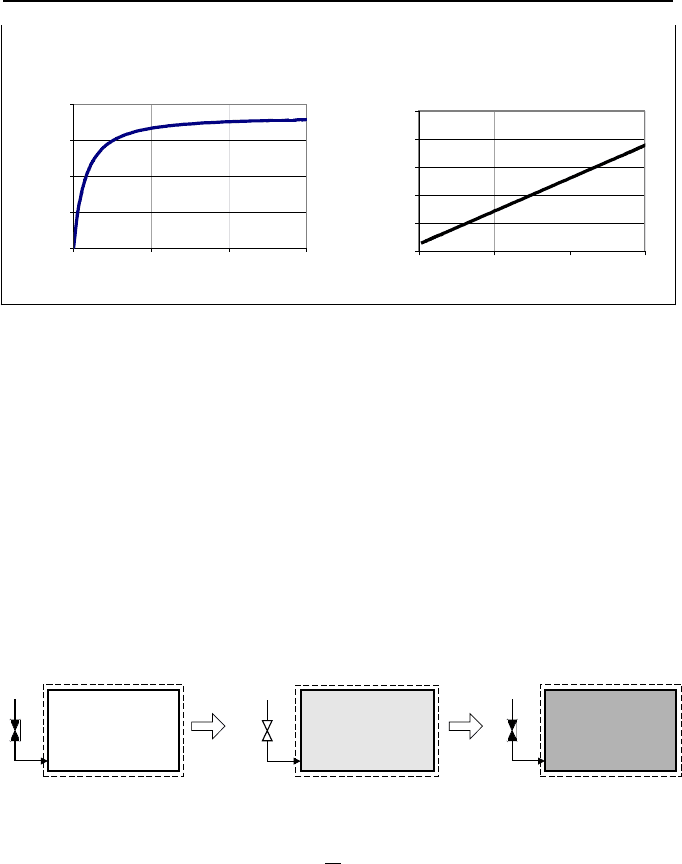
8. Applications of the First Law, Transient 85

minutes, water temperature reaches to about 171.4 F at a level of 7.5 ft from the

bottom of the tank, as plotted in the figure.

100

120

140

160

180

0 600 1200 1800

Time (seconds)

Temperature (F)

0 600 1200 1800

Time (seconds)

Water Level (ft)

8.2. Charging Rigid Vessels (Fixed C.V.) with Gas

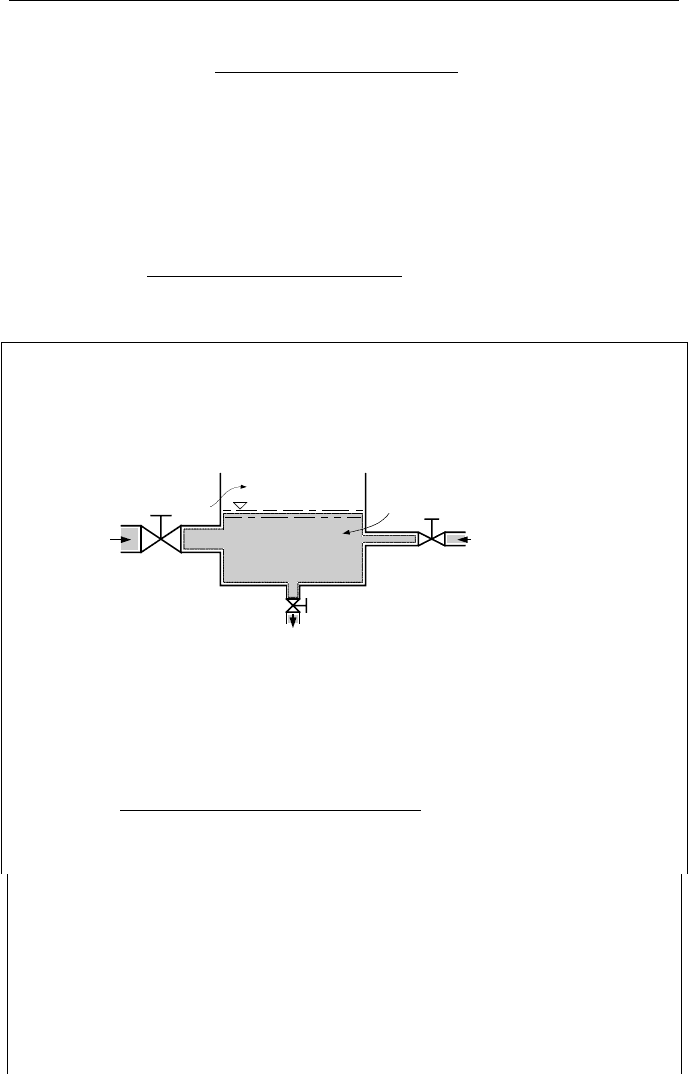
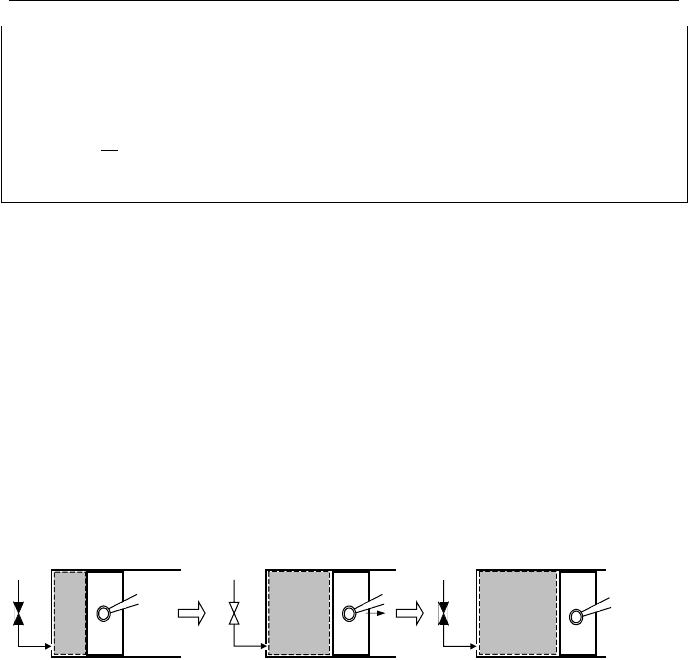
Shown in Figure IIa.8.2(a) is a tank connected to a charging line carrying pressur-

ized gas at a known temperature. Initially, the intake valve is closed and the tank

containing the same gas is at pressure P

and temperature T

. Figure IIa.8.2(b)

shows the condition in the tank after the intake valve is opened. Figure IIa.8.2(c)

shows the final state when the intake valve is closed. For a given initial condition

of the vessel and the inlet enthalpy of the filling gas, we identify two cases to

solve. In case A, having final pressure in the tank, we want to find the final gas

temperature and the average gas mass flow rate entering the tank. In case B, for a

given average mass flow rate of the filling gas, we want to find final pressure and

temperature of the gas in the tank.

& T

P(t)&T (t)

& T

(a) (b) (c)

Figure IIa.8.2. Charging rigid vessels with gas and the associated control volume

Case A. For Given P

, Find T

and



As shown in Figure IIa.8.2, the control volume representing the rigid tank contains

air and is initially at pressure P

and temperature T

. The intake valve is opened to

allow the flow of air into the tank from a high-pressure source. The valve is

closed when the pressure in the tank reaches the specified value of P

. The goal is

to find the average mass flow rate of air entering the tank during the charging

process.

In this case, there is no heat transfer, no shaft work, and no mass leaving the

control volume. Therefore, Equation IIa.6.6 simplifies to:

86 IIa. Thermodynamics: Fundamentals

mud



)(

From the conservation equation of mass (Equation IIa.5.1) we have

iVC

mdtdm



. Substituting, we get:

mud

VC ....

)(

Treating air as an ideal gas (du = c

dT), h

as a constant, and integrating from the

initial state (P

and T

) to the final state where P

is specified yields:

)(

..1122

mmhdmhTcmTcm

iVCivv

−==−

So far, we have one equation and two unknowns, m

and T

. We increase the

number of equations by using the equation of state for state 2:

V = m

air

where V

= V

= V. Substituting for m

from the equation of state in the energy

equation we find m

()()

viuairv

TchmRMcP

112

/V −+

IIa.8.4

Total mass entering the tank is therefore m

= m

– m

and the average mass flow

rate is found from

mm =



where

is the time it took to bring the tank pressure from P

to P

. By eliminating

between the energy equation and the equation of state, we can also obtain an

expression for T

as:

]

)1[(

−

+−=

IIa.8.5

where we have substituted for h

= c

and then

= c

Example II.8.3. A well-insulated tank contains air at 110 kPa and 40 C with the

isolation valve closed. We now open the valve and let pressurized air enter the

tank. We close the valve in 6 seconds when pressure in the tank reaches 130 kPa.

Find the amount of air that has entered the tank. M

air

= 28.97 kg/kmol.

8. Applications of the First Law, Transient 87

P= f

(t)

T = f

(t)

= 140 kPa, T

= 200 C

= 110 kPa

= 40 C

V = 1m

= 130 kPa

= ?

= 140 kPa, T

= 200 CP

= 140 kPa, T

= 200 C

V = 1m

time

Solution: P

= 110 kPa, T

= 40 C (313 K), V = 1 m

. Initial mass of air in the

tank is:

= P

V/RT

= 110 × 1/[(8.314/28.97) × 313] = 1.22 kg

We find h

, assuming constant c

– h

ref

= c

– T

ref

) = 1.0(200 + 273 – 0) = 473 kJ/kg (note h

ref

= 0 at T

ref

= 0 K).

To find m

, we may use Equation IIa.8.4 (or find T

from Equation IIa.8.5 then m

from m

= P

V/RT

33.1

473

)]27340(72.0473[22.1)]314.8/97.28(72.01130[

+×−+×××

=m kg

The mass of air entering the tank is therefore 1.33 – 1.22 = 0.11 kg. To find the

average flow rate, we divided m

– m

by the charging duration: 0.11/6 ≅ 0.02

kg/s. To find T

, we use the equation of state:

= P

V/m

R = 340 K = 67.6 C.

In Example IIa.8.3, we were able to find an analytical solution in a closed form

because the working fluid could be treated as an ideal gas, allowing the use of a

simple equation of state. The reader may try the above example with steam being

the working fluid. In the first try, assume that the container is initially evacuated.

In the second try, assume that the container has steam at atmospheric pressure and

121 C (250 F).

Case B. For Given



, Find P

and T

Given the initial conditions, our goal is to find the final pressure and temperature

of a rigid vessel versus time while the vessel is being charged with an ideal gas at

a specified mass flow rate and enthalpy. We follow the same procedure as in Case

A and this time solve the equation for T

= (m

+ m

)/(m

+ m

Having T

, and m

, we can find P

Example IIa.8.4. A pressure vessel has a volume of 100 ft

(2.83 m

). It contains

air at 1000 psia (~7 MPa) and 150 F (65.5 C). A valve is now opened and highly

pressurized air at a rate of 1 lbm/s (0.453 kg/s) and a temperature of 292 F (144.4

C) enters the vessel. Determine the gas pressure and temperature in the vessel af-

ter 1 minute of charging. R

air

= R

air

= 1545/28.97 = 53.33 ft⋅lbf/lbm·R.

88 IIa. Thermodynamics: Fundamentals

Solution: m

= P

V/R

air

T = (1000× 144)× 100/(53.33× 610) = 442.9 lbm (200

kg)

= [442.9 × 0.171× 610 + (1 × 60) × 0.24 × 752]/[(442.9 + 1 × 60)× 0.171]

= 663 R = 203 F (95 C).

= m

+ =∆tm



442.9 + 1 60× = 502.9 lbm (228 kg)

= m

air

T/V = 502.9 × 53.33 × 663/100 = 1235 psia (8.5 MPa).

8.3. Charging Vessels with Gas (Expanding C.V.)

A cylinder equipped with a frictionless piston contains air at pressure P

and tem-

perature of T

. Our goal is to find the mass of the air entering the cylinder when

the air temperature at the final state reaches T

. As shown in Figure IIa.8.3(a), at

the intitial state (P

, T

) the intake valve is closed. In Figure IIa.8.3(b), the intake

valve has opened, allowing air to enter the control volume. Figure IIa.8.3(c)

shows the final state where the intake valve is again closed and the air temperature

has reached T

. Since the piston is allowed to move, the pressure of the air in the

cylinder remains at P

throughout the filling process. The moving boundary also

requires accounting for the work performed by the piston moving against the at-

mospheric pressure.

T(t)

(a) (b) (c)

Figure IIa.8.3. Charging expanding control volumes: (a) initial state, (b) filling process,

and (c) final state

We now integrate the conservation equations for mass and energy from state 1

to state 2. From the continuity equation, the mass of gas at the final stage is given

as:

= m

+ m

and from the conservation equation of energy we conclude that:

+ m

+ Q = P(V

– V

) +m

We have two equations and three unknowns, m

, m

, and u

for specified m

, u

, h

, Q,

P, V

, and V

. Treating air as an ideal gas, the equation of state becomes PV

, which also satisfies the volume constraint (v

= V

). We now solve for m

= [c

/R – m

– Q +P(V

– V

)]/h

IIa.8.6

8. Applications of the First Law, Transient 89

Example IIa.8.5. A cylinder has an initial volume of 1.0 ft

and contains air at 15

psia (0.1 MPa) and 120 F (49 C). Air at 150 psia (1 MPa) and 250 F (121 C) is in-

jected into the cylinder, pushing the piston to a new position where V

= 3V

. In

the process, 0.2 Btu (211 J) heat is transferred from the cylinder to the surround-

ings. Find the mass of air entering the cylinder and the final air temperature in the

cylinder. R

air

= R

/M = 1545/28.97 = 53.33 ft⋅lbf/lbm·R and c

= 0.171 Btu/lbm·R.

Solution: m

= PV

/RT

= (15 × 144) × 1/[53.33(460 + 120)] = 0.07 lbm

= [0.171 × (15 × 144) × 3/53.33 – 0.07× 0.171 × 580 – (–0.2) + 15 × 144

(3 – 1)/778]/(0.24× 710)

= 0.115 lbm (0.05 kg)

= 15 × 144 × 3/[(0.07 + 0.115) × 53.33 = 657 R = 197 F (92 C).

8.4. Discharging Gas-Filled Rigid Vessels (Fixed C.V.)

Determination of the rate of depressurization of vessels filled with fluids under

pressure poses a challenging task, especially when the vessel is filled with liquid.

Depending on fluid pressure and the rate of discharge, the liquid may change

phase and flash to vapor. Vessel depressurization and flow of two-phase mixture

through pipes are discussed in Chapter Va. Here we deal with an easier task of

analyzing the depressurization of rigid vessels filled with an ideal gas in an isen-

tropic process. For non-isentropic processes, see the accompanying CD-ROM.

The vessel is the control volume. In this ideal process there is no heat transfer

and we assume that the depressurization process is reversible. Therefore, from

Equation IIa.4.4 we have Tv

-1

= constant. Also the volume constraint requires

that V = mv = constant. Taking the derivative of the isentropic relation, we find:

)1(

−= IIa.8.7

Similarly, the derivative of the volume constraint yields:

−=

IIa.8.8

Solving these equations simultaneously, we find that at any point in time we have:

)1/(1

)(

−

IIa.8.9

Substituting from Equation IIa.4.5 into Equation IIa.8.9 yields:

)(

= IIa.8.10

90 IIa. Thermodynamics: Fundamentals

We may also integrate Equation IIa.8.8 to obtain a relationship between mass and

specific volume or between mass and density.

Example IIa.8.6. A tank is filled with air. A valve is opened to vent the tank. If

pressure drops to 1/3 of its initial value find a) the mass of the gas left in the tank

and b) final air temperature. The process is isentropic. Data: V = 2 m

, P

= 6

bar, T

= 230 C. Equilibrium within the tank during the process.

Solution: Treating air as an ideal gas, the initial mass of air is found as:

kg313.8

)273230)(97.28/08314.0(

26V

a) For the isentropic process ==

)( m

8.313 × (1/3)

1/1.4

= 3.79 kg

b) The air temperature drops to:

503)

()(

286.0

×==

−

= 367 K = 94 C

Rapid discharge of pressurized vessels induces thermal stresses in the vessel wall

8.5. Dynamics of Gas Filled Vessels

Earlier we derived the mass and enthalpy of mixing tanks containg a liquid at con-

stant pressure. We want to extend the derivation to vessels containing a gas. We

consider a general case of simultaneous charging of the vessel with the same gas

at several inlet ports and discharging the vessel while heat and shaft work are

added to the vessel as shown in Figure IIa.8.4. The derivation in this case is

mathematically more involved since the gas pressure in the tank changes with

time. Like before, the simplyfing assumptions include a) negligible changes in the

K.E. and P.E., b) instantaneous and perfect mixing of the incoming streams with

the gas in the tank, c) no chemical reaction takes place in the tank throughout the

process, and d) no heat loss from the tank to the surroundings. Expanding the

time derivative term in Equation IIa.6.4-1, using the pefect mixing assumption (h

= h

C.V.

) and substituting from Equation IIa.5.1, we obtain:

()

WQhhm

sii

V+Σ−Σ+−Σ=



IIa.8.11

Since we already used the continuity and the energy equations and have more un-

knows than equations, we now take advantage of the volume constraint; V

C.V.

(mv)

C.V.

= constant or alternatively dV

C.V.

/dt = 0: