Мартыненко Т.П. и др. Практический курс физики. Квантовая физика. Элементы физики твёрдого тела и ядерной физики
Подождите немного. Документ загружается.


51
(
)
xk
2
2
eCx
−
⋅=Ψ
= 0 : + = ;
CkBikAik
211
−
=
−
. :
21
21
kik
kik
AB
−
+
= 1
A
B
R
2
== .
, < U
0
R = 1.
.
.
, ,
> 0 ,
2
2
Ψ = 0.
l,
,
.
xk2
2
2
2
2
eC
−
=Ψ ;
(
)
2
2
2
C0 =Ψ ;
(
)
12
2
2
eC
−
=Ψ l ;
2
k2
1
=l . k
2
,
( )
EUm22
0
−
== ll . , l = 12 .
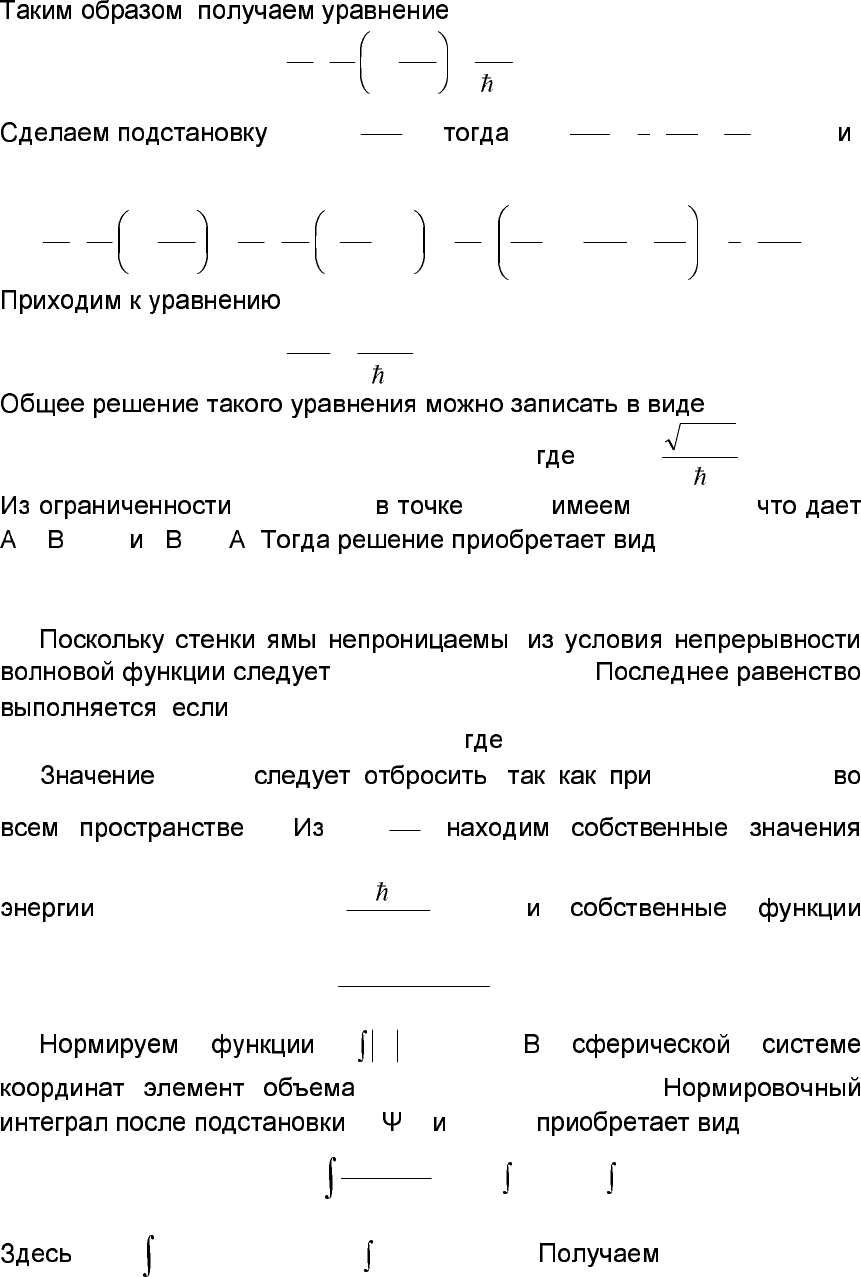
2.14. m -
: U(r) = 0 r < r
0
U(r) = r r
0
. ,
r, )
; ) .
:
0E
m2
2
=Ψ+∆Ψ
-
(r, , ).
:
ϕθ
∆+
∂
∂
∂
∂
⋅=∆
,
2
2
2
r
1
r
r
r
r
1
,
ϕθ
∆
,
.
(
)
0r
,
=Ψ∆
ϕθ
.
52
, :
0E
m2
r
r
r
r
1
2
2
2
=Ψ+
Ψ
⋅
d
d
d
d
.
( )
(
)
r
r
r
χ
=Ψ ;
2
r
dr
d
r
1
dr
d
χ
−
χ
⋅=
Ψ
2
2
2
2
22
2
2
dr
d
r
1
dr
d
dr
d
r
dr
d
r
1
dr
d
r
dr
d
r
1
r
r
r
r
1 χ
⋅=
χ
−
χ
+
χ
⋅=χ−
χ
⋅=
Ψ
⋅
d
d
d
d
0
mE2
dr
d
22
2
=χ+
χ
.
:
rkirki
BeAe
−
+=χ ,
mE2
k = .
r/
χ
=
Ψ
r = 0
(
)
00
=
χ
,
+ = 0 = - . :
(
)
rksinC)ee(A
rkirki
⋅⋅=−⋅=χ
−
,
(
)
0r
0
=
χ
;
(
)
0krsin
0
=
.
,
nrk
0
⋅
π
=
⋅
, n = 1, 2, 3….
n = 0 , n = 0, 0
=
χ
.
0
r
n
k
π
=
2
0
222
n
mr2
n
E
π
=
r
)r/rnsin(C
0
π
=Ψ .
: 1dV
2
=Ψ .
ϕθθ= dddrsinrdV
2
.
dV :
1ddsindrr
r
rksin
C
0
2
0
r
0
2
2
2
2
0
=ϕθθ⋅
⋅
π π
.
2dsin
0
=θθ
π
;
π
π=ϕ
2
0
2d .

53
(
)
2
r
k2
r/nr2sin
r
2
1
k2
)kr2sin(
r
2
1
dr))kr2cos(1(
2
1
drkrsin
0
r
0
0
0
r
0
r
0
0
r
0
2
0
0
0
0
=
π
−=−=−= .
, 1
2
r4C
0
2
=
π⋅
;
0
2
r2
1
C
π
= .
( )
(
)
r
r/nrsin
r2
1
r
0
0
π
⋅
π
=Ψ
2.15.
0 < < l,
(
)
(
)
xAxx
−
=
Ψ
l .
, (2.16),
ΨΨ= dVT
ˆ
*T .
, ,
.
2
222
dx
d
m2m2
p
ˆ
T
ˆ
⋅−== ( . (2.14)).
,
( ) ( )
[ ]
dxxx
dx
d
xx
m2
AT
0
2
22
2
l
ll −⋅−⋅−=
.
,
.
( )
[ ]
2xx
dx
d
2
2
−=−l , ,
T
( )
6
A
m
dxxxA
m
T
3
2
2
0
2
2
l
l
l
⋅⋅=−⋅= .
2
(2.8):
( )
1dxxxA
0
2
22
=−
l
l ;
22
/30A
l
=
.
2
2
m
5
T
l
= .
2
22
dx
d
m2
T
ˆ
H
ˆ
⋅−== .

54
–
.
,
2
2
22
n
n
m
2
E ⋅
π
=
l
.
.
2.16.
ϕ
−= iL
ˆ
z
.
Ψ⋅=Ψ
zz
LL
ˆ
,
ϕ
−= iL
ˆ
z
– , L
z
–
.
, :
Ψ=
ϕ
Ψ
−
z
Li
.
ϕ=
Ψ
Ψ
d
iL
d
z
C
iL
ln
z
+ϕ=Ψ ,
- .
ϕ⋅+ϕ⋅
==Ψ
zz
iL
C
iL
Aee
.
(
)
(
)
π
+
ϕ
Ψ
=
ϕ
Ψ
2 , . .
(
)
π+ϕϕ
=
2iLiL
zz
ee
,
1e
2iL
z
=
π
.
m
2
i
π
⋅
,
...2,1,0m
±
±
=
,
m2
2L
z
⋅π=
π
⋅
;
⋅
=
mL
z
.
, , ,
:
ϕ
=Ψ
mi
Ce
.

55
2.17. ,
1,0 .
= 100 ?
2.18. = 200
= 2 .
.
2.19. ,
t = 0º .
2.20. ,
, - ,
B = 0,5
R = 5 .
2.21.
= 8 10
-24
/ ,
= 50 ?
2.22. m
. : ) ; ) ,
,
,
, .
2.23. ,
.
2.24.
m,
L?
, L~ 10
-15
.
2.25. ,
,
= 10 .
2.26. ,
, .
m, .
= 300 .
2.27.
b = 2,0 .
, , L = 50 ,
= 0,36 .
τ

56
2.28. ,
, ,
L = 75 ,
= 7,5 . d = 25 .
2.29.
= 30°
.
, , d = 0,2 .
U
0
. U
0
, ,
= 2,25 .
2.30. = 180
. ,
= 55° ,
.
, .
2.31.
v, k , :
) ;
) .
2.32. ,
.
2.33.
, = 0,1
2.34. ,
. : 101,9m
31
e0
−
⋅= ,
1067,1m
27
p0
−
⋅= .
2.35.
,
= 1 ?
2.36. R = 0,5
,
= 46·10
3
/4 / . ?
2.37.
0,25
0,6 ?

57
2.38. ,
.
2.39.
1%: ) ; ) , )
- ?
2.40.
= 6 .
?
2.41. – ,
,
:
= 30°;
.
d = 0,24 .
.
2.42. = 11
b = 0,1 .
( ). = b/2.
2.43. ,
,
L = 1 . = L/2.
2.44.
, L = 0,1 .
. = L/2.
2.45. ,
L = 0,1 . = L/2.
2.46. = 10
L = 1 .
. = L/2.
2.47. m L.
,
~ 0,01. = L/2.
2.48. = 0,58
= 10
-8
. ,

58
,
.
2.49. C
. r r
v v.
2.50. ,
min
10 ,
.
2.51. ( = 10 )
. ,
,
2
/
a
=
x
.
p/p
∆
: 1) = 10 ,
2) = 0,1 .
?
2.52.
≥
∆
⋅
∆
t
E
,
,
: 1) ; 2)
( = 10
-8
).
2.53. t = 0
( )
+−=Ψ ikx
a
x
exp·A0,x
2
2
, k –
. :
) ;
) x ;
)
2
x
;
)
x
p
.
2.54. t = 0
( )
+−⋅=Ψ ikx
a
x
expA0,x
2
2
, , k - .
2
Ψ
. ,
2
Ψ .
2.55.
L
:
(
)
(
)
(
)
ikxexpBikxexpA0,x
−
⋅
+
⋅
=
Ψ
. :
) ;

59
) .
2.56.
.
, n
1
= 2 n
2
= 3
E = 0,3 .
2.57.
.
L = 0,1 . ,
.
2.58.
. L
, .
dN/dE, . .
. dN/dE = 1 ,
L = 1 .
2.59.
.
, ) n=3,
) n = 10, ) n = 100.
2.60. m = 10
–26
l = 10 . ,
= 300 , .
?
2.61.
L .
0 < x < L
?
. .
2.62. L
.
L/4, .
2.63.
L
.
L
8
5
xL
8
3
<< .

60
2.64. m
.
a b. :
) (
);
) ;
) ,
n
1
= 2 n
2
= 3
.
2.65.
l.
,
,
2.66. :
( )
−=Ψ
A
r
exp
r
A
r
, r -
, A - . :
) ;
) r .
2.67.
r
0
. ,
( )
(
)
r
r/nrsin
r2
1
x
0
0
n
π
⋅
π
=Ψ , n = 1, 2, 3, …, :
) r ;
)
2
r ;
)
(
)
2
2
rr −=σ .
2.68. ,
(
)
(
)
(
)
rexpr1Ar
β
−
α
+
=
Ψ
, ,
– .
.
2.69.
(
)
(
)
1
r/rexpAr
−
⋅
=
Ψ
, –
,
2
2
0
1
me
4
r
πε
= – .
:
)
;
