Мартыненко Т.П. и др. Практический курс физики. Квантовая физика. Элементы физики твёрдого тела и ядерной физики
Подождите немного. Документ загружается.


41
ϕ⋅=ϕ qQ
ˆ
(2.15)
, q –
Q
ˆ
.
( ) , .
Q
,
Q
ˆ
. Ψ
Q
ˆ
,
Q q,
Q
ˆ
,
Ψ. Q
.
Q
ˆ
, Q
q .
Q .
Q :
*
dVQ
ˆ
Q ΨΨ>=< (2.16)
(2.16) ;
.
, (2.14) (2.13)
:
Ψ⋅=Ψ EH
ˆ
(2.17)
2.1. : 1) ,
10
6
/ , 2) , ,
300 , 3)
10
-3
, 0,1 / .
?
(2.4)
mv
h
p
h
==λ
.
(v<< ) 103,7
10101,9
1062,6
10
631
34
−
−
−
⋅=
⋅⋅
⋅
=λ .

42
v = v , v
m
kT3
=v ,
k=1,38·10
-23
/ . :
1045,1
3001067,11038,13
1062,6
Tkm3
h
vm
h
10
2723
34
−
−−
−
⋅=
⋅⋅⋅⋅⋅
⋅
===λ
1062,6
1,010
1062,6
vm
h
30
3
34
−
−
−
⋅=
⋅
⋅
=
⋅
=λ .
. ,
. ,
, .
,
.
2.2. .
, .
64º,
, .
0,2 ,
.
– ,
λ
=
θ
⋅
k
sin
d
2
.
36,0
=
λ
. v
/102m/hv
6
e
⋅=λ= .
2.3.
,
, .
,
nrm
nn
=
⋅
υ
(1)
n = 1, 2, 3….
υ
==λ
m
h
p
h
(2)
(2)
λ
=
υ
/hm
(1). ,
π
λ
=
2
n
r
n
, ,
:
λ
⋅
=
⋅
π
nr2
n
.

43
2.4. ( )
10
k
=
λ
. ,
.
,
.
:
k
k
h
ch
T ν=
λ
= ,
– . :
1024,11086,19
1010
1031062,6ch
T
514
12
834
k
⋅=⋅=
⋅
⋅⋅⋅
=
λ
=
−
−
−
.
, ,
, 101,5m
52
0
⋅= ,
. . .
,
( )
2
0
cm2TT
ch
⋅+⋅
⋅
=λ
.
2
0
m ,
3,3
=
λ
.
2.5. .
1
– , ,
1,
2
– ,
2.
2
/
1
=3.
1, , , 100
.
, : ) 2? )
? )
– ?
, ,
,
:
2
ACN ⋅=
, N - ,
,
- , –
.
1,
P
1
2

44
12
11
c100CAN
−
== . 2,
12
1
2
22
c900CA9CAN
−
=== ,
.
max
=
1
+
2
= 4
1
.
12
1
2
maxmax
c1600CA16CAN
−
=== .
min
=
2
-
1
= 2
1.
12
1
2
minmin
c400CA4CAN
−
===
2.6.
.
l = 10
-10
.
.
.
U=0.
e
2
m2
p
=E ,
m – .
(2.5) 2/px
x
≈
∆
⋅
∆
.
: l.
l2/p
x
≈
∆
. (2.6)
( )
(
)
2
xx
2
x
ppp −=∆ .
, 0=p
x
.
(
)
2
2
x
2
x
ppp ==∆ .
2
2
2
4
p
l
≈ 110
m8
E
19
e
2
2
=≈≈
−
l
.
2.7. ,
.
:
2
kx
m2
p
E
2
2
x
+= ,
m – , k – .
m
k
=ω . ,
2
xm
m
2
p
E
22
2
x
ω
+= .
(2.6)
( ) ( )
4
ppxx
2
2
xx
2
≈−⋅− .

45
= 0, 0x = , 0=p
x
.
4/px
22
x
2
≈⋅ ;
2
x
2
2
p4
x .
2
x :
2
x
22
2
x
222
x
p42
m
m2
p
2
xm
m2
p
E
⋅
ω
+≈
ω
+=
.
2
x
p , E
0
p8
m
m2
1
pd
Ed
2
2
x
22
2
x
=
ω
−= ,
2
m
p
2
x
ω
=
2
4
4
E
min
ω
=
ω
+
ω
= .
2.8. m E
: U = 0 ( 0), U = U
0
( > 0), U
0
> .
( > 0).
l ,
2.13.
> 0 < U
0
,
.
T = E - U
0
,
.
;
.
T
(
)
(
)
4/ppxx
2
2
xx
2
−⋅− . < U
0
, x > 0 0p
x
= .
,
x > 0:
(
)
2
2
xx l− .
2
2
2
x
4
p
l
≥
2
2
2
x
m
8
m2
p
T
l
≥= .

46
l ,
2.13,
( )
EUm22
0
−
=l , EUT
0
− .
2.9. ,
.
U = 0.
(2.13) :
0E
m2
dx
d
22
2
=Ψ+
Ψ
:
xkixki
eBeA
−
⋅+⋅=Ψ
,
pmE2
k == - . (2.12)
:
( )
( ) ( )
xptE
i
xptE
i
eBeAt,x
+−−−
⋅+⋅=Ψ
,
, –
. = 0.
( )
( )
xptE
i
eAt,x
−−
⋅=Ψ .
( ) ( )
2
xptE
i
xptE
i
2
2
AeeA* =⋅=Ψ⋅Ψ=Ψ
−−−+
.
2
Ψ ,
. ,
,
.
2.10.
,
l ( . .). .
: U( ) = 0 0 < x < l;
U( ) = x 0, x l. ,
- < x < :
I, II, III.
II.
0 x = l X
III
II
I
U(x)

47
,
, . . I III
,
(
)
0x
2
1
=Ψ
(
)
0x
2
3
=Ψ .
,
1
= 0
2
= l
(
)
(
)
000
21
=
Ψ
=
Ψ
;
(
)
(
)
0
32
=
Ψ
=
Ψ
ll (1)
(1) .
II:
0E
m2
dx
d
2
22
2
2
=Ψ+
Ψ
. (2)
(2) , . .
0 < x < l U( ) = 0.
2
2
mE2
k = (3)
λ
π
=
/
2
k
, – .
(3) (2) :
0k
dx
d
2
2
2
2
2
=Ψ⋅+
Ψ
. (4)
(4) :
(
)
(
)
(
)
xkcosBxksinAx
2
⋅
+
⋅
=
Ψ
(5)
– . = 0,
2
(0) = 0
= 0. (5) x = l,
(
)
0ksinA
=
l .
0,
(
)
0ksin
=
⋅
l .
k·l = ·n , n = 1, 2, 3, ... (6)
(3) (6)
:
2
2
22
n
n
m
2
E ⋅
π
=
l
(7)
,
E
1
, E
2
, E
3
…E
n
. ,
, , “ ”
, .
(6)
(
)
(
)
xksinAx
2
⋅
=
Ψ
,
n
,
. (6) :
( )
π
=Ψ
l
nx
sinAx
n,2
(8)
- :
48
( )
=Ψ
l
0
2
n,2
1dxx .
(8),
ll
l
ll
0
2
n
2
n
0
22
n
1A
2
1
dxx
n2
cos1A
2
1
dxx
n
sinA =⋅⋅=⋅
π
−=⋅⋅
π
⋅ .
, l/2A
n
= .
n,2
Ψ
-
)x
n
sin(
2
n,2
⋅
π
⋅=Ψ
ll
.
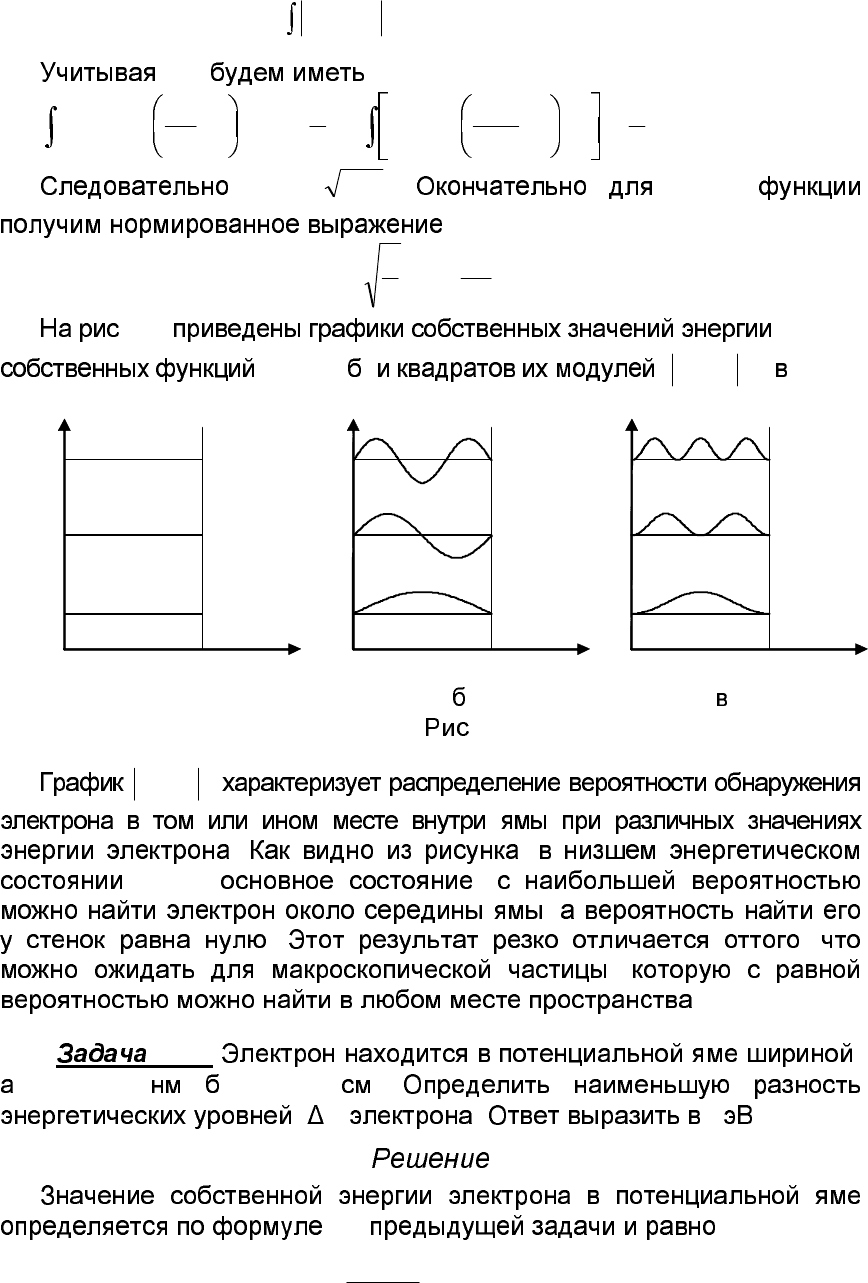
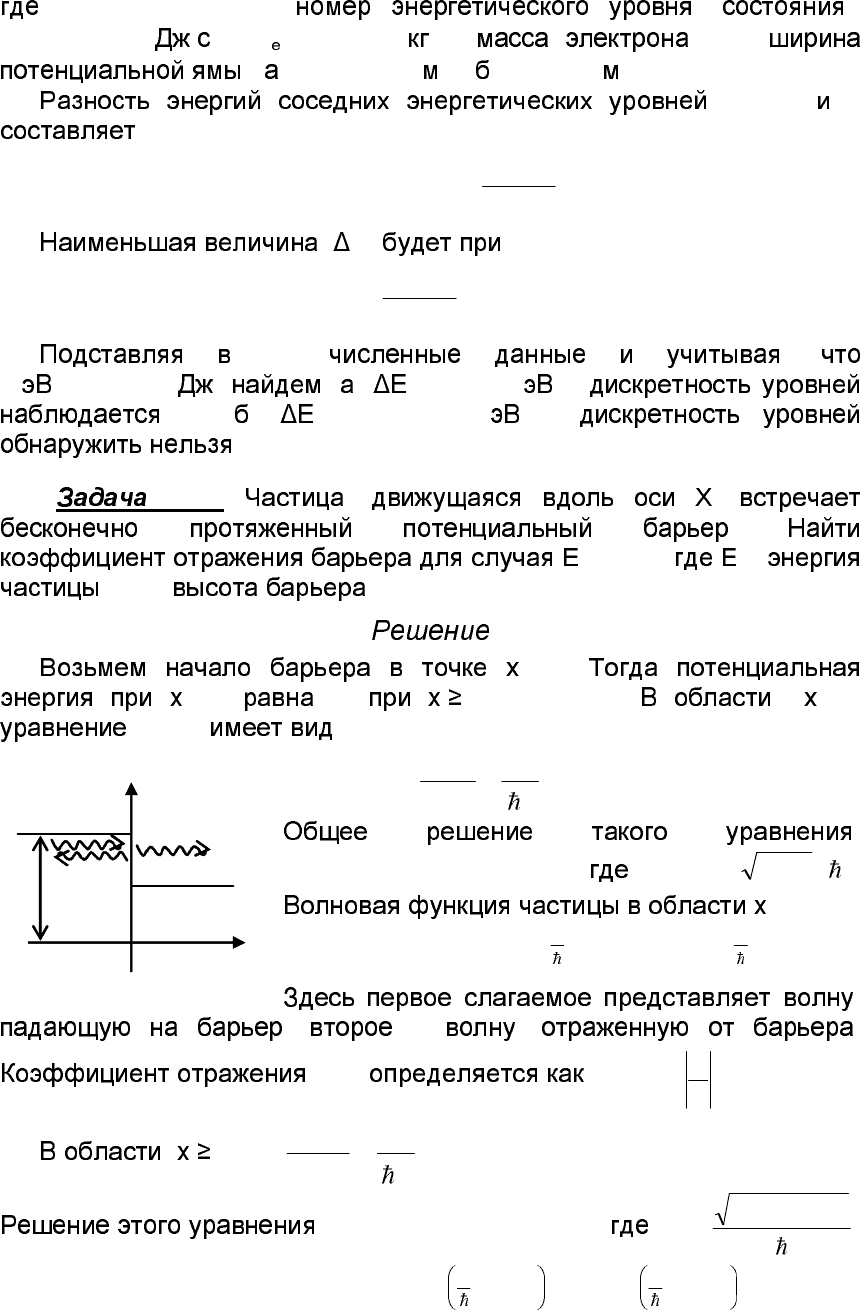
. 2.1 E
n
(a),
(
)
x
n
Ψ
( )
(
)
2
n
xΨ ( ).
(
)
2
n
xΨ
. ,
n = 1 ( )
,
. ,
,
.
2.11. :
) l
1
= 0,45 ) l
2
= 0,9 .
E .
(7)
2
e
22
n
m8
nh
E
l
= , (1)
x
x
x
E
n
n=3
n=2
n=1
0
a)
)
)
Ψ
n
(x)
|
Ψ
n
(x)|
2
l
l
l
. 2.1
0
0
49
n = 1, 2, 3... – ( );
h = 6,62·10
-34
· , m = 9,1·10
-31
– ; l –
: ) l =4,5·10
-10
, ) l =9·10
-3
.
n + 1 n
( )
1n2
m8
h
EEE
2
e
2
n1n
+=∆=−
+
l
(2)
E n = 1
2
e
2
min
m8
h3
E
l
=∆ (3)
(3) ,
1 = 1,6·10
-19
, : )
min
= 5,57 –
; )
min
= 1,39·10
-14
–
.
2.12. , ,
.
/U
0
= 2, –
, U
0
– .
= 0.
< 0 0, 0 U = U
0
. < 0
(2.13) :
0E
m2
dx
d
1
22
1
2
=Ψ⋅+
Ψ
:
xikxik
11
eBeA
−
⋅+⋅=Ψ
, /mE2k
1
= .
< 0
( )
)xkt)xkt
11
eBeAt,x
⋅+−⋅−−
⋅+⋅=Ψ
E
i(
E
i(
,
, – , .
R
2
A
B
R =
.
0: 0)UE(
m2
dx
d
20
22
2
2
=Ψ−+
Ψ
.
:
xikxik
22
eDeC
−
⋅+⋅=Ψ
,
)UE(m2
k
0
2
−
=
;
( )
⋅+−⋅−−
⋅+⋅=Ψ
xktxkt
22
eDeCt,x
E
i
E
i
.
0 x
U(x)
U
0
E

50
,
.
, 0
. , D = 0.
( )
⋅−−
⋅=Ψ
xkt
E
2
eCt,x ,
.
= 0
(
)
(
)
00
21
Ψ
=
Ψ
, + = .
(
)
(
)
00
21
Ψ
′
=
Ψ
′
211
CkBkAk
=
−
.
= + ,
21
21
kk
kk
A
B
+
−
=
(
)
( )
2
21
2
21
kk
kk
R
+
−
= .
k
1
k
2
,
(
)
( )
2
0
2
0
E/U11
E/U11
R
−+
−−
=
.
R = 0,0295.
> U
0
> 0, . .
R = 0. ,
2,95% ,
97,05% > 0.
2.13. = 100
,
U
0
= 150 .
.
< 0
( . 2.12).
( )
⋅+−⋅−−
⋅+⋅=Ψ
xktxkt
11
eBeAt,x
E
i
E
i
0
:
0)EU(
m2
dx
d
20
22
2
2
=Ψ−−
Ψ
:
(
)
xkxk
2
22
eDeCx ⋅+⋅=Ψ
−
,
)EU(m2
k
0
2
−
= .
2
, D = 0.
0 x
U(x)
U
0
E
